可控测角精度和范围的数字阵列单脉冲和差波束优化
马晓峰 沈爱松 盛卫星 韩玉兵 张仁李
可控测角精度和范围的数字阵列单脉冲和差波束优化
马晓峰 沈爱松 盛卫星*韩玉兵 张仁李
(南京理工大学电子工程与光电技术学院 南京 210094)
针对大角度覆盖范围目标快速定位以及机动目标精确角度跟踪的需要,该文提出一种基于可控测角精度和范围的数字阵列单脉冲和差波束迭代快速优化算法。算法可以根据期望的测角精度或期望测角区间,以函数形式给出修正的期望和差波束方向图主瓣区域,然后采用所提出的快速区域加权方向图综合算法闭式优化得到和差波束方向图。该算法通过迭代优化可以在给定输入信噪比和测角精度需求的前提下,最大化单脉冲角度估计的有效测角区间,或者在给定的测角范围内,最优化测角精度。
单脉冲角度估计;方向图综合;测角精度;测角范围
1 引言
传统单脉冲角度估计的和差波束是将两个相同且部分重叠的波束通过和差网络得到。当目标在两波束的交叠轴方向时,和波束输出最大,差波束输出为零。当目标偏离交叠轴一小角度时,可以利用差波束与和波束之比来测角。和差单脉冲角度估计具有系统简单,角度估计精度高等优点,在雷达跟踪系统中得到广泛的应用[1,2]。采用多个天线波束合成的和差单脉冲天线,当天线形式和阵列结构确定后,和差波束方向图以及测角斜率就确定了,其线性测角范围一般在和波束3 dB波束宽度以内,其测角精度完全与和波束输出信噪比相关[3],无法实现测角精度和测角范围之间的权衡和优化。当雷达系统需要在大角度范围内进行目标检测和角度估计时,必须进行大角度范围内的波束扫描[1]。采用数字波束形成技术的有源相控阵雷达则具有更大的方向图综合灵活性,可以通过优化和差波束方向图,有效调节测角精度和测角范围,在不增加信号处理复杂度的前提下,提高目标定位速度。另外,测角精度和测角范围之间进行动态优化,还可以有效地提高雷达跟踪系统针对不同类型机动目标的角度跟踪性能。
测角精度和测角范围联合优化包括两个问题:(1)在期望测角精度条件下,最大化测角范围;(2)在给定测角范围条件下,最优化测角精度。不管是哪方面的优化,都需要建立阵列天线和差波束方向图与测角精度和测角范围之间精确的关系,即通过和差波束方向图与输入信噪比等参数精确获得偏离和波束指向不同位置处的测角精度,然后根据期望的测角精度或测角范围,确定期望的和差波束方向图特性,并通过快速波束赋形算法逼近期望的和差波束方向图。
和差波束角度估计精度是衡量系统测角性能的主要指标,虽然在工程上已经给出了单脉冲角度估计均方误差的近似公式[3],但是对于任意给定权重系数的和差波束,由于没有充分考虑和差波束方向图特性,与理论结果还存在一定的偏差。文献[4]从条件概率分布出发分析了单脉冲比的概率密度函数,文献[5]引入了平均单脉冲比的概念来减少单快拍单脉冲比的波动,即使用多个和差波束输出的快拍信号得到平均单脉冲比,通过计算平均单脉冲比的条件概率密度函数,获得精确的和差波束单脉冲测角精度。
在方向图综合方面,以加权最小均方误差(Weighted Least Mean Squares, WLMS)[6]和加权交替反向投影(Weighted Alternating Reverse Projection, WARP)[7]为代表的最小均方误差优化类算法具有直观的优化目标。文献[8,9]通过快速求解最优期望相位方向图,获得更加逼近期望功率方向图的优化效果,比文献[6,7]利用前次迭代的相位方向图作为下一次迭代的期望相位方向图,具有更快的计算速度。文献[10]通过方向图主瓣区和旁瓣区分区加权功率逼近,在实现较高的主瓣赋形精度以及旁瓣电平控制的前提下,有效降低了算法的运算量。另外,基于迭代傅里叶变换的加速技术也开始应用于大型平面天线进行快速低旁瓣综合[11],并推广到稀疏直线阵[12]、大型稀疏平面阵[13]和快速零陷生成和跟踪[14]的方向图综合中来。
本文算法以文献[5]给出的精确和差波束测角精度公式为基础,提出了一种基于可控测角精度和范围的数字阵列单脉冲和差波束迭代优化算法。该算法可以根据期望测角精度或期望测角区间,以函数形式给出修正的期望和差波束方向图主瓣区域,然后采用快速区域加权方向图综合算法优化和差波束方向图。算法通过多次迭代可以在给定信噪比和测角精度需求的前提下,最大化单脉冲角度估计的有效测角区间,或者在给定的测角范围内,最优化测角精度。非常适合大角度范围内目标搜索和角度估计,以及提高角度跟踪系统对不同类型机动目标的角度跟踪性能。
2 问题方程
2.1 和差单脉冲角度估计模型
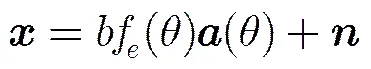
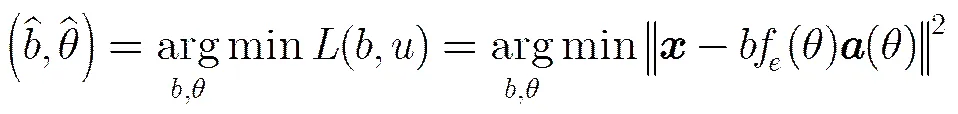
(3)

(5)
(6)
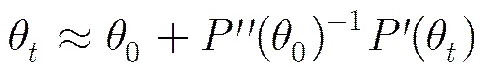
2.2 单脉冲角度估计精度计算
参考文献[5],从条件概率分布出发,通过计算平均单脉冲比的条件概率密度函数,获得精确的单脉冲测角精度。由多个和差波束输出快拍信号计算得到的平均单脉冲比为
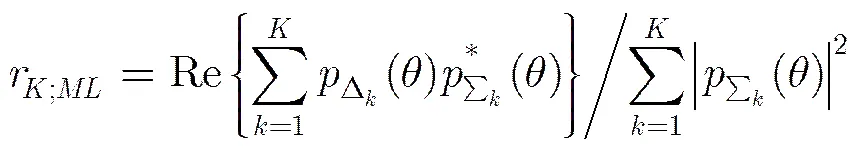
(9)
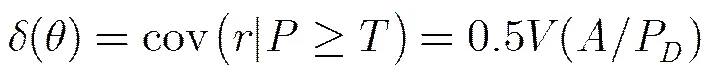
其中,
(11a)
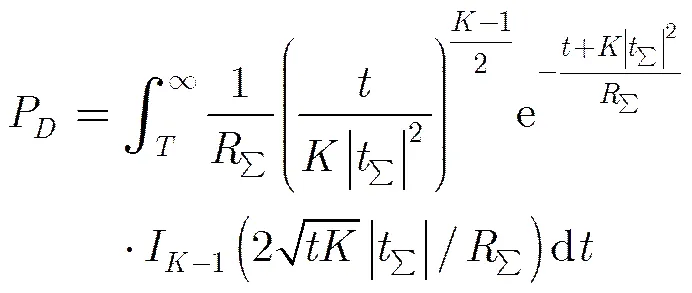
(11c)
2.3 优化问题模型
在单脉冲角度估计,测角精度和测角范围联合优化的应用中,我们需要对两种情况进行优化。

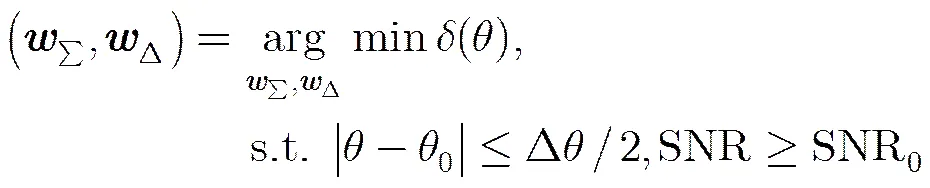
上述两个问题为非线性问题,不能直接求解,第3节将采用方向图赋形迭代逼近技术来优化和差波束方向图,开展上述问题的优化求解。
3 快速优化算法
3.1 期望的和差波束方向图主瓣区形状确定
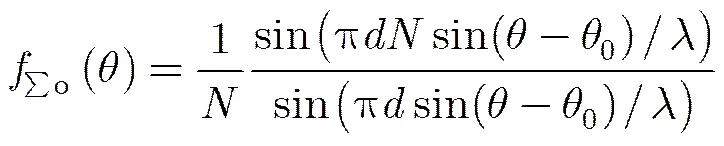
由2.1节分析可知,目标角度的极大似然估计对应的差波束的权重系数可以由和波束权重系数对的导数求得,也就是说,差波束幅度方向图的阵因子可以选取为和波束幅度方向图阵因子的导数,即
(15)
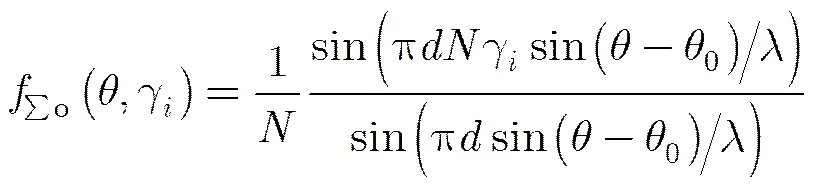
(17)
采用式(16)和式(17)可以作为修正的和波束、差波束主瓣范围期望方向图阵因子。
3.2 和差波束方向图快速优化算法
3.1节已经给出了和差波束主瓣区期望方向图。所需的方向图快速赋形算法应该具有如下特性:(1)主瓣区域尽量逼近期望的方向图主瓣;(2)旁瓣电平尽量低;(3)计算量尽量小。从归一化方向图功率逼近以及区域加权出发,构造和差波束优化算法的代价函数:
(19)
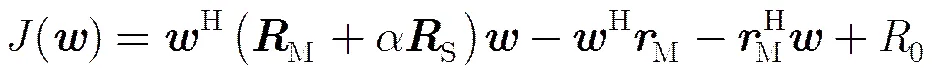
(21a)
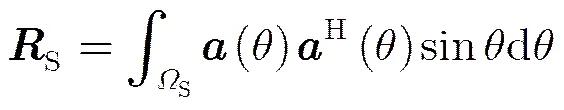
(21c)
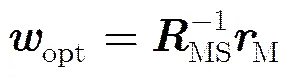
步骤1 根据式(16)和式(17)阵因子定义以及单元天线方向图得到期望的主瓣区幅度方向图;
步骤2 根据式(21a)、式(21b)和式(19)分别计算和;
步骤3 参考文献[9],分别计算主瓣区每个角度的最优方向图相位;
步骤5 根据式(22)直接得到和波束或者差波束的权重系数。
3.3 可控测角精度和范围的单脉冲和差波束优化总流程
步骤5每次迭代均需要判断优化得到的和差波束的测角区间是否优于前一次迭代的结果,从而确定是否结束迭代,这样可以保证算法的收敛性。
同样,针对式(13)的优化问题,在给定阵元最小输入信噪比条件下,在给定测角区间内,最优化角度估计精度的算法具体步骤如下:
4 算法仿真分析
4.1 测角精度分析
首先对2.2节的测角精度公式进行验证。设置和波束权重系数为指向的导向性矢量,差波束权重为和波束权重系数的导数,仿真结果经过10000次蒙特卡罗实验。图1(a)给出当目标方向位于,输入信噪比变化时,统计仿真的单脉冲比均方误差与式(10)计算结果的比较。图1(b)给出输入信噪比为10 dB条件下,目标偏离波束中心的角度变化时,统计仿真的单脉冲比均方误差与式(10)计算结果的比较。
从图1可以看出,式(10)计算得到的结果与统计仿真结果吻合,式(10)可以精确计算给定和差波束,在不同输入信噪比和不同目标角度的测角精度。还可以看到,当目标偏离和波束中心后,测角误差迅速增大,这是因为当目标偏离和波束的3 dB波束宽度范围,和波束增益迅速下降,测角误差急剧增加。此时,虽然在指向附近测角精度很高,但有效测角区间较小,若需要较大的测角区间,需要对和差波束方向图进行优化。
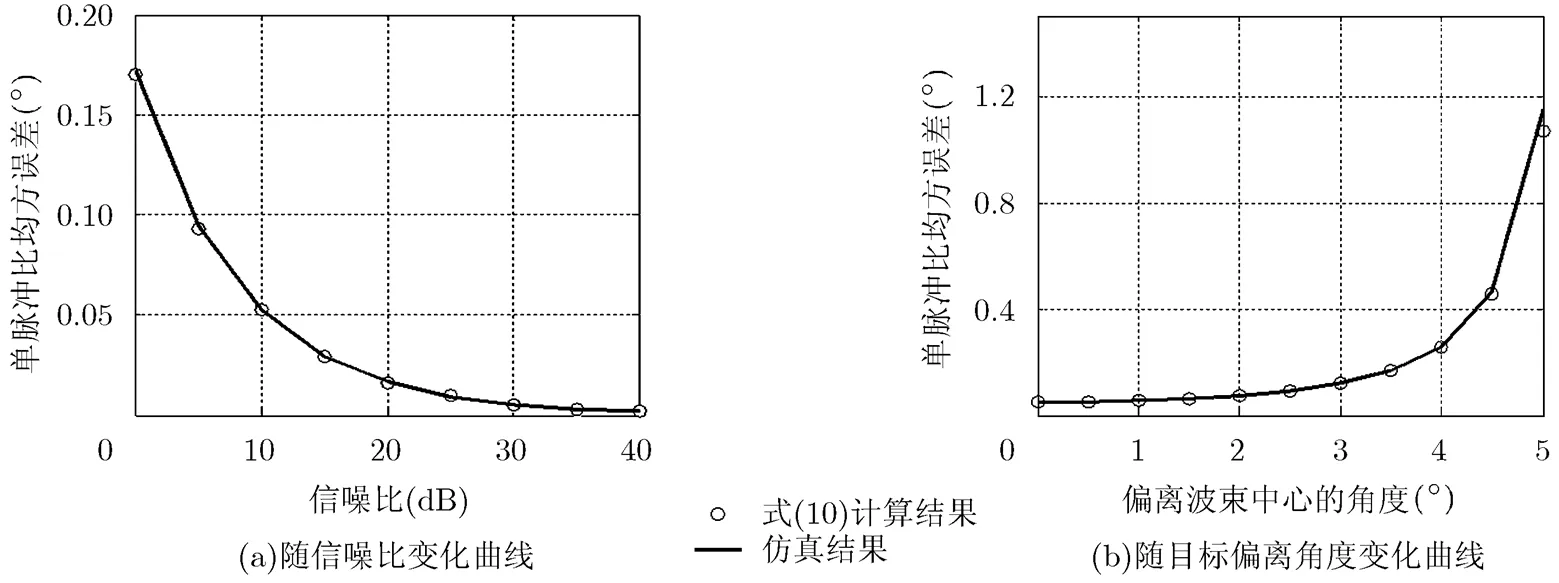
图 1 单脉冲比均方误差仿真结果与式(10)计算结果比较
4.2 最大化测角区间性能仿真
由式(10)计算得到,指向法线方向的初始化和差波束,在输入信噪比为10 dB时,满足测角均方误差小于的测角范围为,现要保持测角精度优于的前提下,最大化有效测角区间。我们设置和差波束方向图允许的主瓣抖动和期望的旁瓣电平分别为和。那么,按照3.3节的算法流程,优化过程如下:
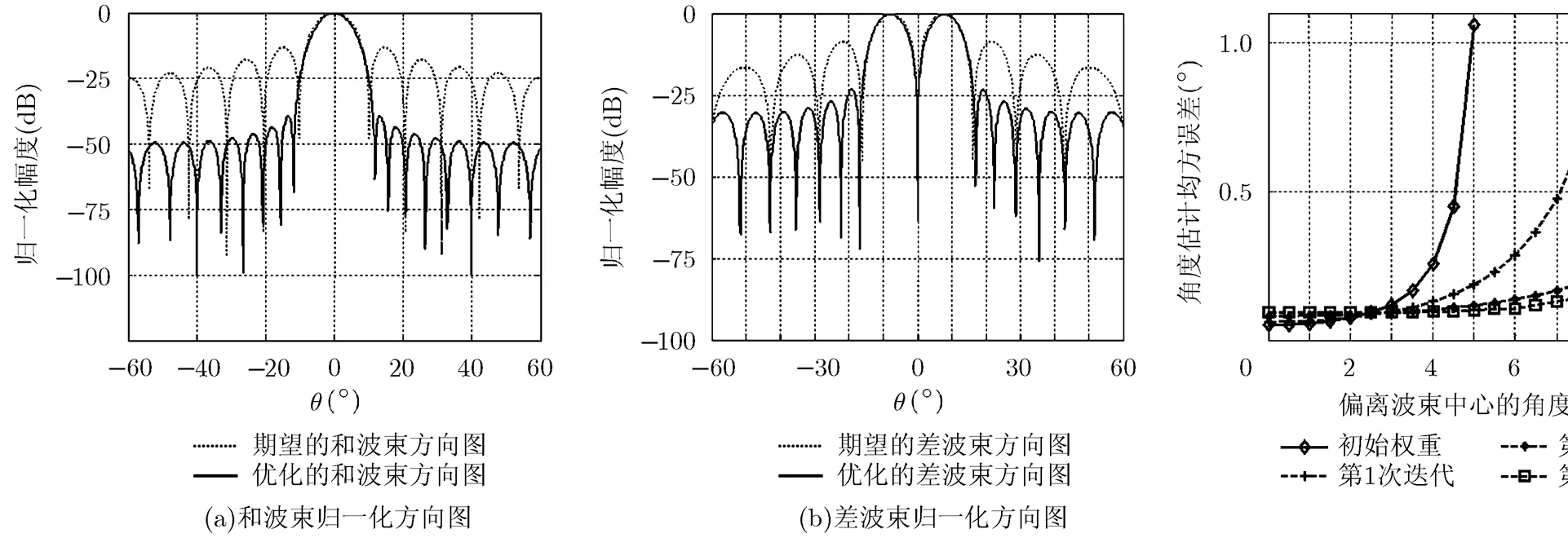
图2 第1次迭代期望和优化得到的和差波束归一化方向图 图3 优化前后侧角误差对比
表1 迭代优化过程中赋形方向图特性与测角性能

迭代次数标号和波束3 dB宽度和波束旁瓣电平(dB)差波束旁瓣电平(dB)测角区间 10.59 7.8-41.6-23.8 8.8 20.3814.4-48.2-28.212.6 30.2918.8-52.9-33.415.6 40.2123.6-59.8-39.215.4
表2 不同波束指向化前后测角区间的变化情况

波束指向015304560 优化前测角区间 6.6 7.8 7.2 7.26.4 优化后测角区间15.616.013.412.89.6
4.3 最小化测角误差性能仿真
同样,由式(10)计算得到,指向法线方向的初始和差波束,在输入信噪比为时,给定测角区间内,波束指向和测角边缘方向的测角精度分别为和,在整个测角区间内测角精度变化较大。下面在给定的测角区间内,最优化角度估计精度。设置。
表3给出了算法每次迭代的优化结果。可以看到,经过两次迭代,测角区间边缘处的测角精度得到了明显提高,在测角区间内的测角精度一致性有效改善。
表3 迭代优化过程中方向图特性与测角性能

迭代次数标号和波束3 dB宽度波束指向的测角区间边缘的 10.4510.00.0670.119 20.3814.40.0850.099 30.3216.80.0880.104

表4 不同波束指向化前后测角精度的变化情况
5 结论
本文提出了一种可控测角精度和测角范围的数字阵列天线单脉冲和差波束优化算法。该算法以精确的单脉冲测角精度公式为基础,通过迭代不断修正期望和差波束方向图,并采用基于快速区域加权最小均方误差波束赋形算法逼近期望的和差波束方向图。修正的期望和差波束方向图主瓣区特性直接以函数形式给出。所提出的快速波束赋形算法代价函数中加权因子直接确定,具有明确的物理意义,并可以直接闭式优化得到最优权重系数。所提出的迭代优化算法得到的和差波束可以在给定输入信噪比和测角精度需求的前提下,最大化单脉冲角度估计的有效测角区间,或者在给定的测角范围内,最优化测角精度。非常适合大角度范围内目标搜索和角度估计,以及提高角度跟踪系统对不同类型机动目标的角度跟踪性能。
参考文献
[1] SKOLNIK M I. Radar Handbook[M]. New York: McGraw Hill, 1990, Chapter 18.3.
[2] MOSCA E. Angle estimation in amplitude comparison monopulse[J]., 1969, AES-5(2): 205-212. doi: 10.1109/ TAES.1969.309906.
[3] YU K B and MURROW D J. Adaptive digital beamforming for angle estimation in jamming[J]., 2001, 37(2): 508-523. doi: 10.1109/7.937465.
[4] TULLSSON B E. Monopulse tracking of Rayleigh targets, a simple approach[J]., 1991, 27(3): 520-531. doi: 10.1109/ 7.81434.
[5] NICKEL U. Performance of corrected adaptive monopulse estimation[J].-,, 1999, 146(1): 17-24. doi: 10.1409/ip-rsn:19990257.
[6] VASKELAINEN L I. Iterative least-squares synthesis methods for conformal array antennas with optimized polarization and frequency properties[J]., 1997, 45(7): 1179-1185. doi: 10.1109/8.596912.
[7] HADDADI A, GHORBANI A, and RASHED-MOHASSEL J. Cosecant-squared pattern synthesis using a weighted alternating reverse projection method[J].&, 2011, 5(15): 1789-1795. doi: 10. 1049/iet-map.2011.0056.
[8] COMISSO M and VESCOVO R. Fast iterative method of power synthesis for antenna arrays[J].&, 2009, 57(7): 1952-1962. doi: 10. 1109/TAP.2009.2021894.
[9] VASKELAINEN L I. Constrained least-square optimization in conformal array antenna synthesis[J]., 2007, 55(3): 859-867. doi: 10.1109/TAP.2007.891860.
[10] 马晓峰, 冯丹萍, 吴玉清, 等. 一种星载阵列天线的高效波束赋形算法[J]. 电波科学学报, 2016, 31(3): 479-485. doi: 10.13443/j.cjors.2015083101.
MA X F, FEN D P, WU Y Q,. An efficient pattern synthesis method for satellite array antenna[J]., 2016, 31(3): 479-485. doi: 10. 13443/j.cjors.2015083101.
[11] KEIZER W P M N. Fast low-sidelobe synthesis for large planar array antennas utilizing successive fast fourier transforms of the array factor[J]., 2007, 55(3): 715-722. doi: 10. 1109/TAP.2007.891511.
[12] KEIZER W P M N. Linear array thinning using iterative FFT techniques[J].,2008, 56(8): 2757-2760. doi: 10.1109/TAP.2008. 927580.
[13] KEIZER W P M N. Synthesis of thinned planar circular and square arrays using density tapering[J], 2014, 62(4): 1555-1563. doi: 10.1109/TAP.2013.2267194.
[14] 马晓峰, 陆乐, 盛卫星, 等. 干扰子空间正交投影快速零陷跟踪波束赋形算法[J]. 电子与信息学报, 2016, 38(10): 2560-2567. doi: 10.11999/JEIT151438.
MA X F, LU L, SHENG W X ,. Fast nulls tracking pattern synthesis based on jammer dubspace orthogonal projection[J].&,2016, 38(10): 2560-2567. doi: 10.11999/ JEIT151438.
[15] NICKEL U. Overview of generalized monopulse estimation[J]., 2006, 21(6): 27-56. doi: 10.1109/MAES.2006.1662039.
[16] NICKEL U. Statistical performance prediction of generalized monopulse estimation[J]., 2011, 47(1): 381-403. doi: 10.1109/ TAES.2011.5705682.
马晓峰: 男,1981年生,讲师,研究方向为阵列信号处理与雷达信号处理.
沈爱松: 男,1994年生,硕士生,研究方向为阵列信号处理.
盛卫星: 男,1966年生,教授,博士生导师,研究方向为阵列信号处理、雷达信号处理与雷达成像等.
韩玉兵: 男,1972年生,教授,博士生导师,研究方向为图像处理、阵列信号处理等.
张仁李: 男,1986年生,副教授,研究方向为雷达信号处理等.
Sum and Difference Patterns Optimization for Digital Array with Controllable Accuracy and Range of Angle Estimation
MA Xiaofeng SHEN Aisong SHENG Weixing HAN Yubing ZHANG Renli
(,,210094,)
A fast iterative optimization algorithm for sum and difference patterns with controllable accuracy and range of angle measurement is proposed, which can be used in fast targets location under wide angle coverage and accurate angle tracking of maneuvering targets. Under expected accuracy or range of angle estimation, the expected main-lobe of sum and difference patterns are modified in the form of sinc function and its derivative respectively, then the sum and difference patterns are rapidly synthesized with the proposed regional weighting pattern synthesis algorithm in the close form. The proposed iterative optimization algorithm can effectively maximize the range of effective angle measurement at a given input signal to noise ratio and angular accuracy, or get optimal accuracy within a given range of angle measurement.
Monopulse angle estimation; Pattern synthesis; Angle estimation accuracy; Angle estimation range
TN957.51; TN820.1+2
A
1009-5896(2016)12-3107-07
10.11999/JEIT160873
2016-08-24;改回日期:2016-12-08;
2016-12-14
盛卫星 shengwx@njust.edu.cn
国家自然科学基金(61501240, 11273017),上海航天基金重点项目(SAST201437)
The National Natural Science Foundation of China (61501240, 11273017), The Key Project of Shanghai Aerospace Foundation of China (SAST201437)

