一种新的干涉相位图局部自适应滤波方法

薛海伟 冯大政



一种新的干涉相位图局部自适应滤波方法

薛海伟*冯大政

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

为了有效提高对InSAR干涉相位噪声的抑制性能并充分保持干涉相位图细节信息，该文提出一种基于局部地形相位补偿和各向异性高斯滤波函数(AGF)的自适应复相位滤波方法。该方法首先利用局部频率估计方法补偿地形相位，以便于消除局部地形相位对滤波窗口内干涉相位的不利影响。然后，构造了尺度和方向自适应的AGF，并对同分布样本进行局部加权的方向滤波。这里，AGF尺度随相干系数等级自适应变化：在低相干区域，采用的大尺度AGF能够充分地抑制相位噪声；在高相干区域，采用的小尺度AGF能更好地保持相位细节信息。AGF方向根据最大加权相干积累准则确定，以选取同分布的滤波样本估计中心像素相位值。实验结果表明，与多种滤波方法相比，该文方法在减少干涉相位图残点和保持条纹边缘等方面均具有更好的性能。

干涉合成孔径雷达；相位噪声滤波；相位噪声模型；频率估计；各向异性高斯滤波

1 引言

干涉合成孔径雷达(InSAR)测量技术利用从不同位置不同视角观测同一场景获得的两幅相干SAR图像来生成复干涉相位图，并进行高程重建得到观测场景的数字高程图(DEM)[1]。由于系统噪声及各种去相干因素的影响，干涉相位图中存在明显的噪声，严重影响了相位展开、高程重建等后续处理的性能。因此，干涉相位滤波是InSAR高程重建过程中的一个关键步骤，对于降低相位展开难度、提高高程测量精度都具有重要的意义。

目前，国内外提出了多种干涉相位滤波算法，其中多视滤波器[7]被认为是在最大似然意义下最优的。但是，多视滤波器常采用固定的滤波窗口，在相位细节信息保持和条纹密集区域滤波效果之间很难取得平衡。Goldstein等人[8]针对小块干涉图频谱，提出了一种在保持相位谱情况下将幅度谱进行幂运算，实现条纹连续性保持的自适应滤波器，但因该方法取固定的幂指数，其噪声抑制效果欠佳。随后，Baran等人[9]让该算法中的幂指数随相干系数自适应变化。文献[10]根据干涉条纹的方向和密度调整滤波窗口的大小和方向，然后进行中值或均值滤波，但该方法未能实现自适应强度滤波。Trouvé等人[11]在线性相位补偿的基础上采用较大的滤波窗口对残余相位进行复多视处理，减少了残点数目。在文献[11]的工作基础上，Cai等人[12]根据相干积累准则提出一种窗口大小自适应的局部频率估计方法，对修正后的相位进行复均值滤波。但这两种方法[11,12]都没有进行样本点的选取，滤波性能欠佳。利用干涉相位条纹的方向信息，Lee等人[13]从16个方向性滤波窗口中选择具有最大复均值的方向窗口，并将当前窗内的相位平均值与中心像素相位观测值进行线性组合得到中心像素相位的估计；该方法滤波精度较高，且避免了对高相干区域的过度滤波，但选择的方向窗口可能不与条纹方向完全平行，从而导致条纹出现断裂，且在滤波之前需进行局部相位预展开，这会引起较大的误差。Wu等人[14]根据局部条纹频率确定局部条纹方向，取方向窗与条纹方向完全平行，先利用插值计算滤波窗内的相位值，然后采用文献[13]方法实现自适应滤波；该方法能够更有效地保持条纹边缘，且不需要局部相位预展开，获得了良好的滤波性能。文献[15]通过限定滤波样本值选取范围和去除相位外点等措施改进了文献[13]滤波方法。Suo等人[16]采用自适应尺寸的滤波窗口、相位坡度补偿以及滤波参数修正等措施进一步改进了文献[8]方法，在保持相位边缘连续性的同时提高了噪声抑制性能。文献[17]首先利用分块后的相位图频谱和半功率门限估计主要地形相位，然后采用简化的文献[13]滤波形式对残余相位进行滤波。李锦伟等人[18]首先借助外部数字模型反演干涉条纹并利用方向性窗口估计相干系数，对样本进行最小噪声方差意义下的最优加权滤波，取得了较好的滤波效果。

为了在有效抑制噪声的同时避免破坏条纹信息，并选取同分布滤波样本进行自适应强度的滤波，本文提出了一种基于局部地形相位补偿和各向异性高斯滤波函数(AGF)的自适应复相位滤波方法。该方法利用局部地形相位补偿获得同分布样本，并采用方向和尺度自适应的AGF实现滤波样本选取和自适应强度滤波，可以充分抑制低相干区域的相位噪声，并且能保持高相干区域的相位细节信息，即使在条纹密集区域，也能够兼顾噪声抑制和细节信息保持。最后采用仿真和实测数据对本文方法的性能进行了验证。

2 干涉相位模型

InSAR中两幅SAR图像的相干性直接影响高程测量的精度，而相干性受到系统噪声、基线去相干、时间去相干和图像配准误差等因素的影响。衡量相干性大小的相干系数定义为

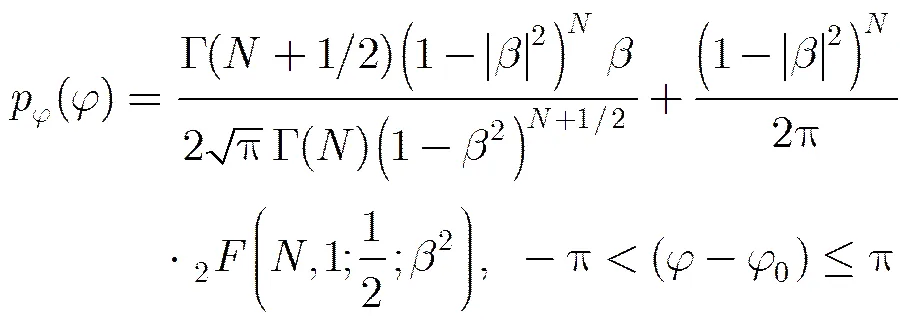
(3)

实际中由于获得SAR图像数量的限制，通常对滤波窗口内样本进行空间平均来实现多视处理。但多视处理要求局部相位满足同分布，且抑制相位噪声的同时会降低图像的分辨率。由于复杂地形的影响，相位图不同区域的相干性不同，且局部滤波窗口内的滤波样本不满足同分布的条件，特别在地形变化剧烈的地区。因此在相位滤波之前需要首先补偿地形引起的相位，并选取同分布滤波样本进行滤波，同时还需要避免对高相干性区域过度滤波导致的分辨率损失。

图1 干涉相位噪声标准差与相干系数和视数的关系

3 算法原理

由于InSAR测量中两个雷达具有不同的观测位置，获得的干涉相位会随着观测场景的高度起伏和水平距离而变化[1]。本文方法基于局部平稳的假设，首先估计并补偿局部地形坡度引起的相位，然后自适应地选取满足同分布的滤波样本。为此，将局部地形相位看作由以下两部分组成：地形坡度引起的线性相位和偏离这一坡度的地形分量引起的相位，同时将式(3)扩展表示为

(6)

3.1 局部地形坡度相位估计

观测场景内的地形是不断变化的，但通常可以假定为局部平稳的。即把干涉图划分为许多较小的窗口后，每个窗口对应的局部观测区域内的地形倾斜角是一致的。具有不同视角的雷达观测倾斜角无变化的地形，所得到的干涉相位在距离方向和方位方向都只包含一个主要频率，可表示为一个2维正弦模型[19]：

(8)

由于随机分布噪声和残余地形相位的影响，窗口内的滤波样本不完全满足同分布。为了获得更好的滤波性能，还需要采取进一步的措施选取滤波样本。

3.2 基于AGF的自适应滤波

针对滤波窗口内样本选取的问题，本文基于2维AGF生成尺度自适应于局部相干系数等级且方向连续变化的支撑区域，然后根据复相位平面内最大加权相干积累准则，采用2维极坐标傅里叶变换快速确定支撑区域的方向信息。方向自适应AGF选取的滤波样本更加满足同一分布，提高了相位滤波精度；尺度自适应于局部相干系数等级的AGF能够有效抑制低相干区域的相位噪声，同时保护高相干区域的相位条纹细节信息。

水平方向的AGF表示为

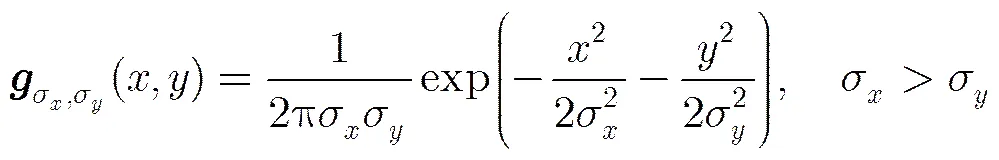
(10)

3.2.1 尺度自适应 为了避免对高相干区域过度滤波导致分辨率损失，需要根据相干系数等级来决定滤波的强弱。根据式(4)，高相干系数区域只需要相对较少的滤波样本就可以达到与低相干区域类似的滤波效果，即高相干系数区域需要较小的支撑区域，因此我们根据局部相干系数等级调整支撑区域大小，实现自适应强度滤波。尺度为,的AGF等效滤波窗口大小为[20]，根据式(4)，和为

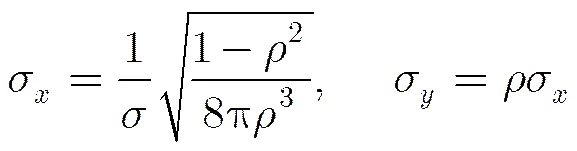
图2 AGF支撑区域示意图

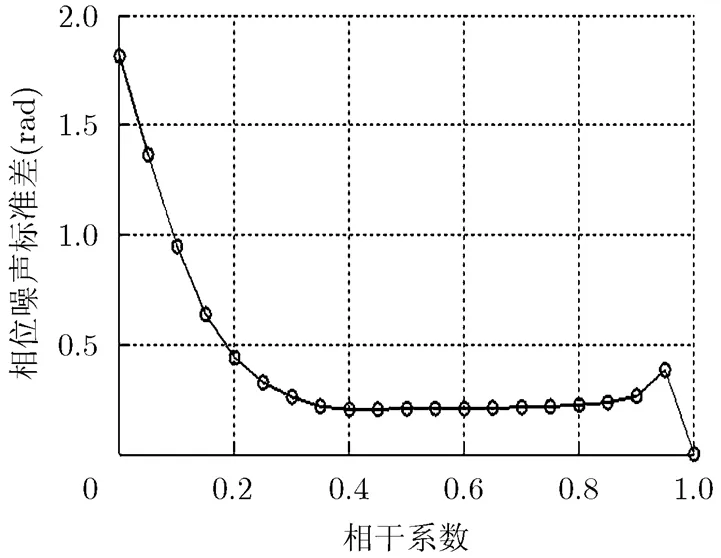
图3 自适应尺度AGF滤波效果图

3.2.2 方向自适应 为了选取更加满足同分布的滤波样本，需要估计支撑区域的方向信息。考虑相位受到噪声的影响及存在以为周期的模糊性，方向信息以最大加权相干积累作为准则自适应地确定。考虑到极坐标变换可以把难以匹配的角度旋转变换为坐标轴方向的平移，本文利用2维极坐标傅里叶变换快速估计支撑区域的方向信息。首先，将残余相位窗口中心移到坐标原点，并将直角坐标系中的点变换为极坐标系中的点，变换定义为

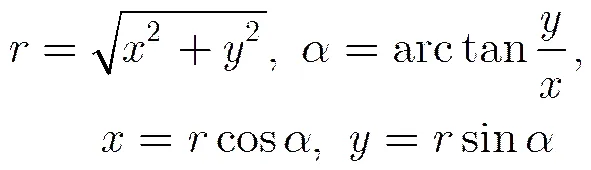
(13)

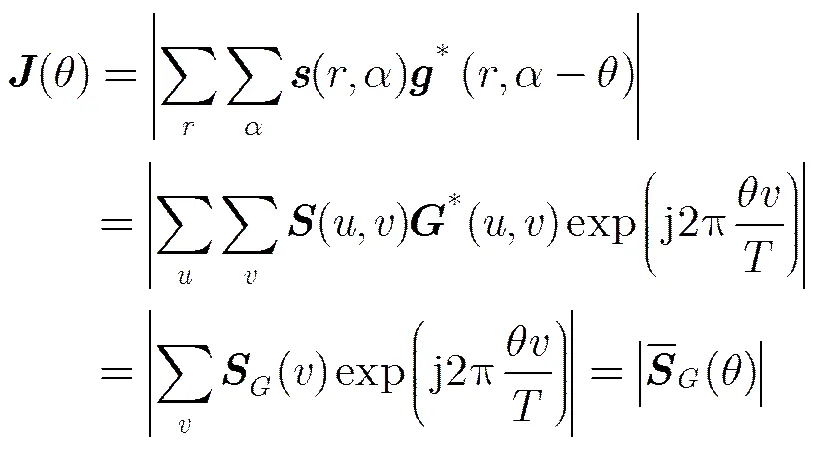
(15)

(17)

3.3 算法步骤

本文方法利用各向异性高斯函数生成各向异性的支撑区域，并根据局部噪声分布自适应地选择干涉相位滤波样本实现局域加权的方向滤波。具体步骤如下：

(2)利用式(8)估计局部地形相位，将地形相位从原始干涉相位中去除得到残余相位；

(3)根据式(11)确定AGF尺度；

(4)基于最大加权相干积累准则，利用2维极坐标傅里叶变换快速估计AGF的方向信息。根据式(16)生成2维高斯滤波函数；

(5)在复数平面上，根据式(17)对残余相位进行滤波，得到像素的残余相位估计值；

4 实验结果

本节分别利用仿真数据和实测数据分析本文滤波方法的性能，并与改进Goldstein滤波器[8]、Lee自适应复滤波器[13]和文献[11]提出的相位坡度补偿方法进行了比较。

图4所示为对一组仿真数据进行滤波的结果。图4(a)为不含噪声的仿真干涉相位图，由MATLAB中的Peaks函数生成，干涉相位尺寸为像素。根据文献[13]的加性噪声模型，加入了标准差为1 rad的相位噪声，如图4(b)所示。改进Goldstein滤波器的分块尺寸为32，重叠尺寸为14，采用窗口平滑频谱幅度。Lee滤波器采用滤波窗口，16个方向窗口。本文方法中设置为0.2。图4(c)至图4(f)为各方法的滤波结果。从图4所示滤波图像视觉比较可以发现：改进Goldstein滤波器分块之间出现不连续性，对噪声抑制不够充分，整个图像内还存在大量的噪声，性能最差。Lee滤波器在条纹密集处性能下降，多数条纹变得模糊甚至出现断裂的现象，相位细节信息保持性能较差。文献[11]方法滤波结果中明显存在一定数量的孤立点噪声，性能较好。本文方法不仅有效地抑制了噪声，而且获得了完整清晰的干涉相位图，即使在条纹密集区域相位条纹边缘也保持了良好的连续性，性能最好。为了更加直观地比较各方法的滤波性能，我们采用相位偏差和残点滤除率来衡量滤波算法的性能。图5所示为上述各方法滤波结果与原始相位图的相位偏差直方图，滤波前后的残点对比结果见表1。可以看出，本文方法滤波结果比其他方法更加接近原始相位图，并且更有效地降低了残点数目，具有更好的滤波降噪性能。

采用两组实测数据以进一步评估本文滤波方法的性能，分别为：X-SAR录取的Etna火山口的数据和TerraSAR-X卫星获取的澳大利亚艾尔斯岩石数据，经过图像配准和去平地相位处理后，生成的原始干涉相位图如图6所示，Etna数据和艾尔斯岩石数据的尺寸分别为像素和像素。利用本文方法与改进Goldstein滤波器[8]、Lee滤波器[13]和文献[11]方法对图6所示两组数据进行滤波处理，实验结果如表1和图7所示。表1列出了上述各方法滤波后干涉相位图中残点的数目，通过对比可以看出，本文方法相对于其他方法更加有效地减少了残点数目。从图7(a)至图7(d)所示对Etna数据滤波结果比较发现：改进Goldstein滤波结果中存在大量的残点；Lee滤波器和文献[11]方法能够比较有效地减少残点数目，但是在条纹密集区域性能不佳，条纹连续性被破坏，如图7(b)、图7(c)中白框内区域所示；本文方法获得的结果图像中残点数目最小，并且更大程度地保持了相位条纹的细节信息，即使是在条纹密集区域，相位边缘也保持了良好的连续性，如图7(d)中白色圆框所示。对艾尔斯岩石数据进行滤波处理也得到了同样的结果，如图7(e)至图7(h)所示。综上，从滤波结果和对剩余残点的统计结果可以看出，与其他几种方法相比，本文方法能够获得更加清晰的干涉相位图，在条纹密集区域性能优势更加明显，表明本文方法能够在对噪声进行有效抑制的同时充分保持干涉相位图的细节信息。

图4 仿真干涉相位滤波结果比较

图5 相位偏差直方图              图6 实验采用的两组数据

表1 各方法对仿真数据、Etna数据和艾尔斯岩石数据滤波后的残点数目比较

滤波方法仿真数据Etna数据艾尔斯岩石数据 残点数残点减少(%)残点数残点减少(%)残点数残点减少(%) 原始干涉相位图22598-97657-46494- 改进Goldstein滤波器[8]1272243.702670572.65 949779.57 Lee滤波器[13] 159892.931310586.58 288793.79 文献[11]方法 89096.06 732592.50 397391.45 本文方法 9499.58 142598.54 81998.24

计算复杂度方面，改进Goldstein滤波器由于逐块进行滤波，运行时间最短。Lee滤波器、文献[11]方法和本文方法均是逐像素进行滤波，Lee滤波器需要定位方向窗和计算加权系数，文献[11]方法仅估计局部相位坡度，本文方法需要估计局部地形相位和自适应AGF的参数，因此在局部窗口大小相同的条件下，本文方法计算复杂度高于改进Goldstein滤波器和文献[11]方法，比Lee滤波器略高。表2所示为各方法的运行时间(CPU: 3.6 GHz，内存：32.0 G)。

表2 各方法运行时间

滤波方法运行时间(s) 仿真数据Etna数据艾尔斯岩石数据 改进Goldstein滤波器 6.859 26.699 23.206 Lee滤波器119.067465.891372.797 文献[11]方法 56.254213.550187.089 本文方法132.114502.934435.183

5 结束语

本文提出了一种有效抑制干涉相位噪声并同时保持干涉相位图细节信息的自适应复相位滤波方法。与传统空域滤波相比，本文方法具有以下优势：其一，方法首先对局部地形斜面引起的相位进行估计并补偿，降低了局部地形对干涉相位的影响，更有利于选取同分布样本进行滤波；其二，AGF尺度自适应于相干系数提供不同程度的平滑效果[20]，具体来讲：低相干区域采用大尺度AGF生成较大的有效支撑区域，提供了较大的平滑度，以确保相位噪声得到足够的抑制；而高相干区域采用小尺度AGF生成较小有效支撑区域，能够更好地保持相位细节信息。其三，AGF方向根据最大加权相干积累准则确定，使得AGF支撑区域内选取的滤波样本更加满足同分布，提高了滤波精度，同时AGF方向可利用2维极坐标傅里叶变换快速确定。仿真和实测数据处理结果验证了本文方法的性能。

参考文献

[1] ROSEN P A, HENSLEY S, JOUGHIN I R,. Synthetic aperture radar interferometry[J]., 2000, 88(3): 333-382. doi: 10.1109/5.838084.

[2] LIN X, LI F F, MENG D D,. Nonlocal SAR interferometric phase filtering through higher order singular value decomposition[J]., 2015, 12(4): 806-810. doi: 10.1109/LGRS. 2014.2362952.

[3] CAO M Y, LI S Q, WANG R,. Interferometric phase denoising by median patch-based locally optimal wiener filter[J]., 2015, 12(8): 1730-1734. doi: 10.1109/LGRS.2015.2422788.

[4] LI H Y, SONG H J, WANG R,. A modification to the complex-valued MRF modeling filter of interferometric SAR phase[J]., 2015, 12(3): 681-685. doi: 10.1109/LGRS.2014.2357449.

[5] LI J W, LI Z F, BAO Z,. Noise filtering of high- resolution interferograms over vegetation and urban areas with a refined nonlocal filter[J]., 2015, 12(1): 77-81. doi: 10.1109/LGRS.2014. 2326462.

[6] SONG R, GUO H D, LIU G,. Improved Goldstein SAR interferogram filter based on adaptive-neighborhood technique[J]., 2015, 12(1): 140-144. doi: 10.1109/LGRS.2014.2329498.

[7] SEYMOUR M S and CUMMING I G. Maximum likelihood estimation for SAR interferometry[C]. International Geoscience and Remote Sensing Symposium, 1994, 4: 2272-2275. doi: 10.1109/IGARSS.1994.399711.

[8] GOLDSTEIN R M and WERNER C L. Radar interferogram filtering for geophysical applications[J]., 1998, 25(21): 4035–4038. doi: 10.1029/1998GL900033.

[9] BARAN I, STEWART M P, KAMPES B M,. A modification to the Goldstein radar interferogram filter[J]., 2003, 41(9): 2114-2118. doi: 10.1109/TGRS.2003.817212.

[10] FU S H, LONG X J, YANG X,. Directionally adaptive filter for synthetic aperture radar interferometric phase images[J]., 2013, 51(1): 552-559. doi: 10.1109/TGRS.2012.22. 2911.

[11] TROUVE E, NICOLAS J M, and MAITRE H. Improving phase unwrapping techniques by the use of local frequency estimates[J]., 1998, 36(6): 1963-1972. doi: 10.1109/36.729368.

[12] CAI B, LIANG D N, and DONG Z. A new adaptive multiresolution noise-filtering approach for SAR interferometric phase images[J]., 2008, 5(2): 266-270. doi: 10.1109/ LGRS.2008.915942.

[13] LEE J S, PAPATHANASSIOU K P, AINSWORTH T L,. A new technique for noise filtering of SAR interferometric phase images[J]., 1998, 36(5): 1456-1465. doi: 10.1109/36. 718849.

[14] WU N, FENG D Z, and LI J X. A locally adaptive filter of interferometric phase images[J]., 2006, 3(1): 73-77. doi: 10.1109/ LGRS.2005.856703.

[15] CHAO C F, CHEN K S, and LEE J S. Refined filtering of interferometric phase from InSAR data[J]., 2013, 51(12): 5315-5323. doi: 10.1109/TGRS.2012.2234467.

[16] SUO Z Y, ZHANG J Q, LI M,. Improved InSAR phase noise filter in frequency domain[J]., 2016, 54(2): 1185-1195. doi: 10.1109/TGRS.2015.2476355.

[17] WANG Q S, HUANG H F, YU A X,. An efficient and adaptive approach for noise filtering of SAR interferometric phase images[J]., 2011, 8(6): 1140-1144. doi: 10.1109/LGRS.2011. 2158289.

[18] 李锦伟, 李真芳, 刘艳阳, 等. 一种相干系数加权的最优干涉相位滤波[J]. 西安电子科技大学学报, 2014, 41(2): 25-31. doi: 10.3969/j.issn.1001-2400.2014.02.005.

LI J W, LI Z F, LIU Y Y,. Coherence-weighted optimum interferometric phase filtering method[J]., 2014, 41(2): 25-31. doi: 10.3969/ j.issn.1001-2400.2014.02.005.

[19] SUO Z Y, LI Z F, and BAO Z. A new strategy to estimate local fringe frequencies for InSAR phase noise reduction[J]., 2010, 7(4): 771-775. doi: 10.1109/LGRS.2010.2047935.

[20] SHUI P L and ZHANG W C. Noise-robust edge detector combing isotropic and anisotropic Gaussian kernels[J]., 2012, 45(2): 806-820. doi: 10.1016/ j.patcog.2011.07.020.

薛海伟： 男，1985年生，博士生，研究方向为干涉SAR数据处理、SAR成像.

冯大政： 男，1959年生，教授，博士生导师，研究方向为雷达成像、阵列信号处理、盲信号处理、神经网络等.

New Locally Adaptive Method for InSAR Phase Noise Filtering

XUE Haiwei FENG Dazheng

(,,710071,)

In order to effectively suppress the noise of InSAR phase images and preserve the detailed fringe information, an adaptive phase filtering method based on local slope compensation and the Anisotropic Gaussian Filter (AGF) is proposed. Firstly, the topography-induced phase is approximately measured by local frequency estimation and removed from the original phase to eliminate the effect of the terrain topography. Secondly, the AGF with adaptive scale and orientation is developed to directionally filter out the noisy phase for the pixels with more homogeneous phase values. The scale of the AGF varies adaptively with the local coherence: a large-scaled AGF can better smooth the noise of low coherence areas, whereas a small-scaled AGF can better preserve the phase details of high coherence areas. Moreover, the orientation angle of the AGF is fast determined to select the identically distributed samples according to the maximum weighted coherent summation principle. The experimental results obtained via simulated and real data show that compared with commonly used filters, the proposed method achieves better performance in terms of residue reduction and fringe preservation.

Interferometric SAR (InSAR); Phase noise filtering; Phase noise modeling; Frequency estimation; Anisotropic Gaussian Filter (AGF)

TN957.51

A

1009-5896(2016)12-3085-08

10.11999/JEIT161013

2016-09-30；改回日期：2016-11-25；

2016-12-14

薛海伟 xuehw001@163.com

国家自然科学基金(61271293)

The National Natural Science Foundation of China (61271293)