多站ISAR空间目标姿态估计方法
周叶剑 张 磊 王虹现 邢孟道 牛 威
多站ISAR空间目标姿态估计方法
周叶剑①②张 磊*①②王虹现①②邢孟道①②牛 威③
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(西安电子科技大学信息感知技术协同创新中心 西安 710071)③(宇航动力学国家重点实验室 西安 710043)
该文提出一种基于多站逆合成孔径雷达(ISAR)序列成像的空间目标姿态估计方法。方法提取各帧ISAR图像中目标的典型线性结构,结合目标轨道信息实现关键部件姿态估计。该文建立了较为稳健的空间目标ISAR几何结构分析流程,采用Radon变换对太阳能翼、平板天线等线性结构进行提取和关联,继而估计典型线性结构在距离-多普勒成像平面的姿态角变化,同时利用卫星轨道信息获得ISAR距离-多普勒投影矩阵进行线性结构的3维姿态解算,最终实现典型部件姿态的优化求解估计。仿真实验验证了所提算法可有效实现空间目标典型部件的姿态估计,同时利用多站ISAR观测数据可有效提升算法的估计精度。
ISAR成像;几何投影矩阵;姿态估计;Radon变换;多站ISAR
1 引言
精确实时测量空间目标以及重要载荷部件的姿态指向是空间目标监测的重要内容,目标姿态信息可有效反应空间目标工作状态,可直接应用于目标故障分析,特别对非合作空间目标及其载荷的主动姿态估计可分析其载荷指向、动作意图等重要情报。目前,空间目标的绝对姿态估计主要利用光电或雷达传感器对目标进行连续高分辨成像,根据图像序列信息来进行目标的姿态估计。这种外部观测方式可应用于合作目标也可应用于非合作目标甚至是失控目标的姿态估计[1,2]。对于成像序列信息的利用上,观测者又可以根据实际需求采用不同方案。其中基于观测图像与参考数据库的匹配是一种较为可行的方案。在已知目标几何材质、空间构造的情况下,通过电磁或光学仿真建立目标观测数据库,对窄带RCS序列、宽带逆合成孔径雷达(ISAR)、光学等成像方式得到的图像进行模板或者特征匹配,根据匹配结果确定观测目标真实3维姿态。另外一种方案则是基于观测的几何投影模型,直接根据观测图像进行目标姿态和3维结构的重建,如:使用激光传感器对目标点云进行特征值分解或者各特征提取,来获得目标姿态信息[6,7];使用雷达传感器对目标表面点进行跟踪观测,结合目标2D雷达图像与空间3D目标模型之间的联系完成3维目标姿态的重建。上述算法均是针对目标散射点进行建模和处理,对散射中心的视角变化较为敏感。在目标结构复杂、有效散射中心缺失或者被遮挡的情况下,散射中心的精确提取较为困难,难以满足当前观测任务的需求。
考虑到当前空间目标姿态估计的主要目的是确定载荷等关键部件的空间指向,而实际应用中大多数载荷存在明显的线性结构这一特点,本文提出一种基于逆合成孔径雷达(ISAR)序列成像的空间目标线性部件姿态估计方法。通过单/多站ISAR系统获取空间目标的连续观测数据,使用距离-多普勒算法对回波进行成像,利用Radon变换对得到的雷达序列图像进行典型线性结构(如卫星所配备太阳能翼、平板天线等重要载荷部件)的提取,并进行线性结构的序列关联。然后从经典的几何投影理论出发,结合目标轨道参数、观测站点位置信息构造各站点所对应的ISAR距离-多普勒观测投影矩阵,来匹配观测到的图像序列解算出这些结构在空间中的姿态信息,完成关键部件运行状态的评估,实际可应用于包括民用卫星载荷工作状态判定、故障分析,军事目标威胁度评判、捕获等民用和军用领域。
2 空间目标ISAR几何投影分析
地基ISAR系统空间观测过程中,目标的空间位置可通过坐标转换从空间目标轨道坐标转换到地心固定坐标(ECEF)[10,11],继而考虑雷达站点坐标可得到雷达视角信息[4,11],如图1(a)所示。在多站观测的情况下,为保证目标姿态描述的统一性,经过理想的平动补偿后,雷达视角信息已由ECEF坐标转换到目标本体坐标系下,如图1(b)所示。
在完成雷达视角信息的转换后,本文采用经典的3维转台模型来描述目标相对雷达视线的姿态角变化。如图2(a)所示,假设某一测量瞬时,目标相对雷达视线仰角和方位角分别表示为和,则瞬时雷达视线方向表示为

图1 空间目标观测几何
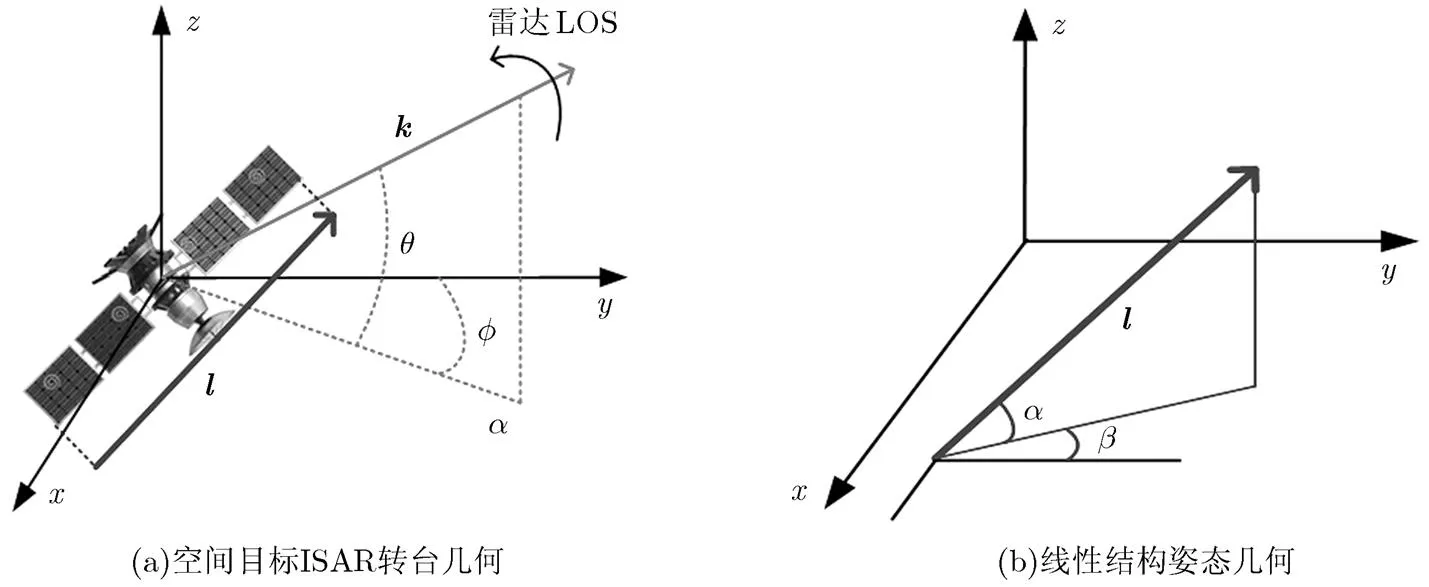
图2 空间目标转台模型与线性结构姿态模型
空间目标通常装配太阳能帆板、SAR平板天线等重要兴趣载荷,其边缘均有严格的线性结构特征。如图2(b)所示,定义某一太阳能翼边缘为兴趣线性结构,定义2维姿态角和,则该线性结构姿态指向可用单位矢量表示为

考虑ISAR成像采用距离-多普勒(RD)处理,雷达图像距离和多普勒像素分辨率定义为[12]
(3)
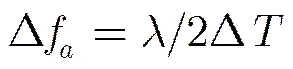

(6)
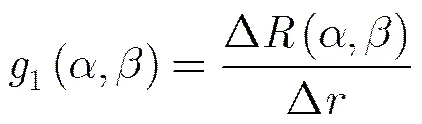
(8)
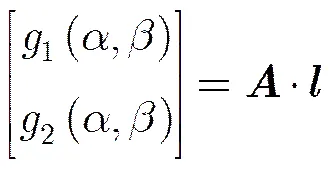
(10)
式中
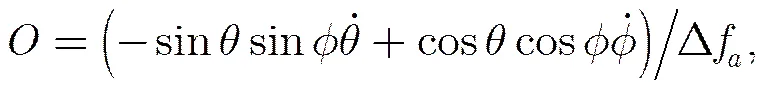
也就是说已知空间目标相对于各站点的雷达视线参数,构造相应的投影矩阵,可以对线性结构指向(即在图2几何空间中的目标绝对姿态角和)在雷达图像上的投影信息进行预测。
3 线性结构提取与姿态估计
本文提出的线性结构姿态估计算法利用地基ISAR系统对空间目标的连续观测数据获得目标的ISAR图像序列,从图像序列中提取目标线性结构在2D雷达图像上的指向信息作为观测数据。然后,通过雷达视线信息建立投影矩阵序列,对目标线性结构在2D雷达图像上的指向信息做出预测。接着,构造代价函数,搜索使预测信息最接近观测信息的姿态角参数,作为3D空间中线性结构的真实指向,从而完成对目标整体姿态的估计。需要强调以下两个因素:(1)空间目标在单帧RD成像相干处理时间内姿态相对平稳、视角变化可近似为2维转台模型,单帧RD图像中目标投影对应该帧相干处理时间中间点的目标姿态;(2)每帧RD图像具有足够分辨率和聚焦精度,可分辨目标线性结构。
本文算法具体流程如图3所示。首先根据得到的回波数据,采用传统ISAR处理流程进行RD序列成像;然后对得到的图像序列进行目标线性结构的提取,获取其在RD成像平面内的倾角、长度、中心位置等观测信息;接着通过空间目标轨道信息及站点位置信息构造各帧图像对应的投影矩阵,利用观测几何进行图像间线性结构的关联并完成目标线性结构的绝对姿态角估计。下面对各核心步骤详细说明。

图3 ISAR序列像的线性结构提取与姿态估计流程
3.1 RD序列成像
3.2 线性结构提取
首先对各帧RD图像进行滤波、对数变换,提高RD图像平滑性并调整像素值范围,在此基础上采用-mean聚类算法[13]进行背景分割得到目标-背景的二值图像。继而进行图像形态学处理提取目标边界,形态学处理主要利用腐蚀、膨胀、开运算、闭运算[14,15]。
空间目标的太阳能翼、平板天线等典型线性结构是本文所关心的特征结构。进行以上图像处理后,这些典型目标线性结构主要体现在二值图像的边界信息中,这里对边界图像进行Radon变换,提取感兴趣的线性结构,并记录每帧图像中各线性结构在图像中的指向倾角,中心位置,长度作为观测信息。
3.3 投影矩阵构造和线性结构的关联
3.3.1 同站图像间的关联 定义归一化的差别函数描述相邻图像间线性结构的相似程度,归一化差别函数如式(11):

3.3.2 异站图像间的关联 定义指向倾角间的关联系数描述不同图像间线性结构的相似程度:
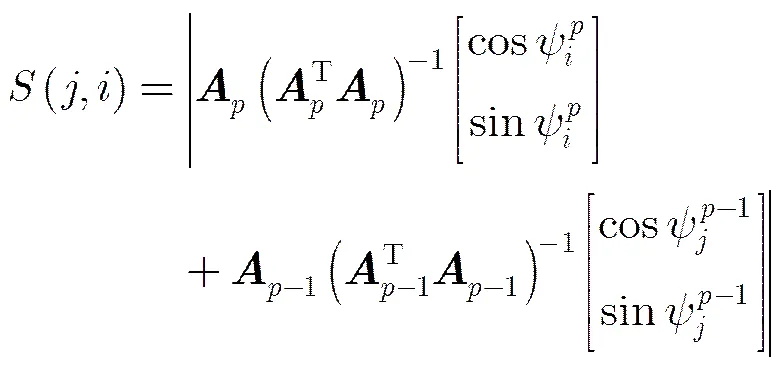
通过最小化式(11)或式(12)中的代价函数,实现相邻帧间不同线性结构的关联,遍历各帧RD图像,即可实现各线性结构在不同帧间的有效关联。需要说明的是由于多站情况下,不同站点对应的投影矩阵间变化不连续,当倾角信息提取中出现较大的干扰时,可能存在关联失败的情况,实际处理多站ISAR图像结构的关联可引入部分人工认证处理以保证准确性。
3.4 姿态参数优化估计
本文算法的姿态参数优化估计主要从预测信息与观测信息间的差别最小化出发对目标绝对姿态仰角和方位角进行估计。对第帧RD图像可有如式(13)所示测量方程:
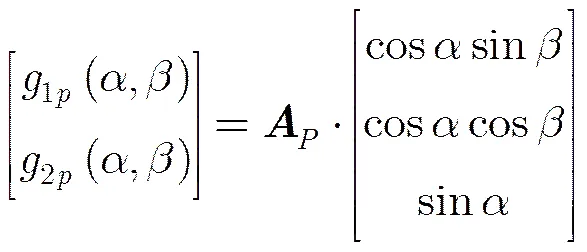
(14)

需要强调线性结构姿态估计的优化问题运算量非常小,这里使用简单的枚举法搜索代价函数最小值。
4 仿真实验分析
仿真实验使用一组真实目标轨道参数下仿真卫星目标的连续回波,卫星目标3维模型如图4所示。该目标太阳能翼为可折叠平板结构,具有明显的线性边界。仿真主要分为单站观测与多站观测两部分,采用的主要ISAR雷达参数如表1所示,选取的目标轨道、雷达站点位置信息如表2所示。

图4 卫星目标3维结构模型
表1 主要ISAR系统参数

单帧RD成像尺寸512×512 波长0.018 m 发射信号的带宽1 GHz 发射信号中心频率16.7 GHz 脉冲重复频率100 Hz
表2 目标轨道及观测站点位置信息

目标轨道高度791 km 目标轨道倾角 目标轨道升交点赤经 北京站位置 佳木斯站位置
4.1 单站观测情况下的目标姿态估计
本实验在北京站对处于轨道某段的目标进行仿真。
首先对连续观测回波进行角域划分并RD成像,得到包含15帧ISAR图像的观测序列,RD图像信噪比设置为20 dB,图像横纵坐标分别表示方位向、距离向像素位置而无具体量纲。
对图像序列进行图像处理后,利用本文方法对处理后图像序列进行线性结构的提取、关联,选取其中4帧图像关联结果如图5所示。最后,对关联后的3个线性结构,分别进行优化估计获取其绝对姿态角参数,并与真值进行比较,结果如表3所示。
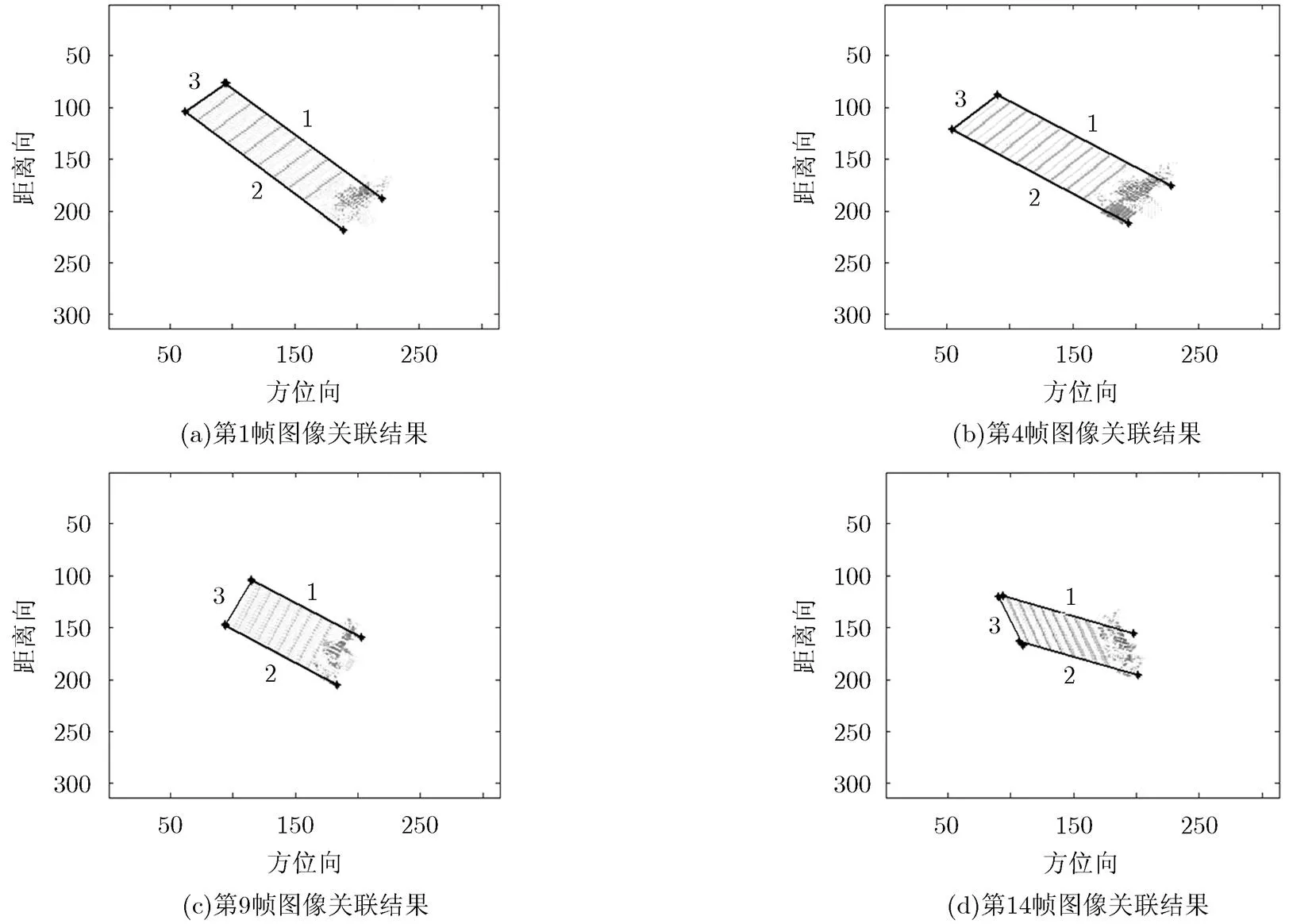
图5 雷达图像线性结构关联结果
表3 线性结构姿态估计

结构编号123 姿态仰角-9.6-10.075.5 方位角171.3172.1121.5 空间真实指向矢量liang 量(-0.14, 0.98, 0.17)(-0.14, 0.98, 0.17)(0.20, -0.14, 0.97) 估计误差0.510.371.05
从实验过程来看,单站算法性能主要受两方面影响。第一是图像处理精度,特别是边界提取精度对线性结构在RD平面姿态角的估计影响较大;第二是RD图像本身受目标相对雷达视角的约束,在某些视角下,RD图像中线性结构特征表现不明显。此外,单站算法需要较长时间的连续观测,也就是依赖获取的图像帧数。
4.2 多站观测情况下的目标姿态估计
针对单站方法的局限性,本部分实验在多站观测模式下进行目标姿态的估计。选取同一观测时间段内,北京站3帧(第1, 2, 3帧),佳木斯站3帧(第4, 5, 6帧)观测结果进行线性结构的关联与提取,关联结果如图6所示,姿态估计的结果如表4所示。

图6 多站观测下目标线性结构关联结果
表4 多站观测下线性结构姿态估计

结构编号123 姿态仰角-13.3-15.7-12.7 方位角69.1163.268.3 空间真实指向矢量矢量(0.91, 0.36, -0.22)(-0.30, 0.92, 0.26)(0.91, 0.36, -0.22) 估计误差1.021.480.04
如图6所示,本实验北京站的观测图像结果不佳(主要是线性结构的完整度受到观测视角的影响),线性结构提取的结果存在明显误差,若仅采用北京单站数据进行估计则结果将存在较大误差,而联合佳木斯站的观测数据后,估计的平均误差仍在之内如表4所示。也就是说,多站联合观测进行姿态估计可有效克服单站估计误差受雷达视角的限制,且其在观测时间从15帧对应的观测时间下降至3帧对应的观测时间的情况下将算法的估计精度维持在一定水平,这对实际应用中目标姿态稳定性要求的降低具有较大的意义而随之带来的只有多站观测间的时间同步要求,具有较强的可操作性[16,17]。
5 结束语
本文从几何投影理论出发,分析目标2维雷达图像与空间3维目标模型之间的联系,通过雷达视线信息来预测空间目标线性部件在2维雷达图像中的投影信息。同时,通过一系列图像处理操作获取空间目标线性部件在ISAR图像的观测信息。最后,搜索与观测信息最相近的预测信息所对应的姿态参数作为姿态估计结果。本文实验结果表明本文算法在单站观测较为完备的情况下,准确度较高,同时推广至多站模式可有效克服单站算法的局限性,可满足实际的空间目标姿态估计任务。本文算法对ISAR图像序列的信噪比要求偏高,对图像处理精度要求亦偏高,在后续工作中,可对算法中背景分割、线性结构提取等步骤进行改良,进一步提高算法的准确度与稳定性。
参考文献
[1] Lefferts E J, Markley F L, and Shuster M D. Kalman filtering for spacecraft attitude estimation[J].,, 1982, 5(5): 417-429.
[2] 徐少坤, 刘记红, 袁翔宇, 等. 基于 ISAR 图像的中段目标二维几何特征反演方法[J]. 电子与信息学报, 2015, 37(2): 339-345. doi: 10.11999/JEIT140338.
XU Shaokun, LIU Jihong, YUAN Xiangyu,. Two dimensional geometric feature inversion method for midcourse target based on ISAR image[J].&, 2015 37(2): 339-345. doi: 10.11999/JEIT140338.
[3] 魏小峰, 耿则勋, 娄博, 等. 空间目标三维姿态估计[J]. 武汉大学学报, 2015, 40(1): 96-101. doi: 10.13203/j.whugis2013 0156.
WEI Xiaofeng, GEN Zexu, LOU Bo,. A 3D pose estimation method for space object[J]., 2015, 40(1): 96-101. doi: 10.13203/j.whugis20130156.
[4] Zhong W J, Ji J S, Lei X,. The attitude estimation of three-axis stabilized satellites using hybrid particle swarm optimization combined with radar cross section precise prediction[J]., 2015, 8: 1-13. doi: 10.1177/0954410015596178.
[5] Lemmens S, Krag H, Rosebrock J,. Radar mappings for attitude analysis of objects in orbit[C]. Proceedings of the 6th European Conference on Space Debris, Darmstadt, Germany, 2013: 20-24.
[6] Zhu D Q and Chu C C. Characterization of irregularly shaped bodies[C]. International Society for Optics and Photonics, USA, 1995: 17-22. doi: 10.1117/12.211501.
[7] 郭裕兰, 万建伟, 鲁敏, 等. 激光雷达目标三维姿态估计[J]. 光学精密工程, 2012 20(4): 843-850. doi: 10.3788/OPE. 20122004.0843.
GUO Yulan, WAN Jianwei, LU Min,. Three dimensional orientation estimation for ladar target[J]., 2012 20(4): 843-850. doi: 10.3788/ OPE.20122004.0843.
[8] Tomasi C and Kanade T. Shape and motion from image streams: A factorization method[J]., 1993, 90(21): 9795- 9802. doi: 10.1007/BF00129684.
[9] Rosebrock J. Absolute attitude from monostatic Radar measurements of rotating objects[J]., 2011, 49(10): 3737-3744. doi: 10.1109/TGRS.2011.2159727.
[10] 宁夏, 叶春茂, 杨健, 等. 空间目标雷达观测视角变化率及其应用[J]. 清华大学学报(自然科学版), 2013 53(11): 1558-1564. doi: 10. 16511/j.cnki.qhdxxb. 2013.11.008.
NING Xia, YE Chunmao, YANG Jian,. Radar aspect angle rate-of-change with respect to space target and its application[J].(), 2013, 53(11): 1558-1564. doi: 10.16511/j.cnki. qhdxxb.2013.11.008.
[11] Mayhan J T, Burrows M L, Cuomo K M,High resolution 3D “Snapshot” ISAR imaging and feature extraction[J].,2001, 37(2): 630-642. doi: 10.1109/ 7.937474.
[12] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 231-241.
BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 231-241.
[13] Elhabian S Y, ElSayed K M, and Ahmed S H. Moving object detection in spatial domain using background removal techniques-state-of-art[J]., 2008, 1(1): 32-54. doi: 10.2174/1874479610801010032.
[14] Rafael C G and Richard E W. Digital Image Processing [M]. Third Edition. Beijing: Publishing House of Electronics Industry, 2007: 432-435.
[15] 刘艳莉, 桂志国. 基于形态学的可变权值匹配自适应图像增强算法[J].电子与信息学报, 2014, 36(6): 1285-1291. doi: 10.3724/SP. J.1146.2013.01082.
LIU Yanli and GUI Zhiguo. Adaptive image enhancement algorithm with variable weighted matching based on morphology[J].&, 2014, 36(6): 1285-1291. doi: 10.3724/SP.J.1146. 2013.01082.
[16] 陈伯孝, 朱旭花, 张守宏. 运动平台上多基地雷达时间同步技术[J]. 系统工程与电子技术, 2005, 27(10): 1734-1737. doi: 10. 3321/j.issn:1001-506X.2005.10.020.
CHEN Boxiao, ZHU Xuhua, and ZHANG Shouhong. Time synchronization technique of multi-station radar on moving flat[J].,2005, 27(10): 1734-1737. doi: 10.3321/j.issn:1001-506X.2005.10.020.
[17] 刘赞, 陈西宏, 薛伦生, 等. 双基地雷达系统时间同步方案研究[J].火力与指挥控制, 2016, 41(1): 139-142. doi: 10.3969. j.issn.1002-0640.2016.01.034.
LIU Zan, CHEN Xihong, XUE Lunsheng,. Research on schemes of the time synchronization for bistatic radar system[J].&, 2016, 41(1): 139-142. doi: 10.3969/j.issn.1002-0640.2016.01.034.
周叶剑: 男,1993年生,博士生,研究方向为ISAR成像.
张 磊: 男,1984年生,副教授,研究方向为SAR/ISAR成像与运动补偿.
王虹现: 男,1979年生,副教授,研究方向为雷达成像及其实时处理.
邢孟道: 男,1975年生,教授,研究方向为SAR/ISAR成像.
牛 威: 男,1977年生,高级工程师,研究方向为雷达目标特性分析、雷达信号处理.
Attitude Estimation for Space Satellite Targets with Multistatic ISAR Systems
ZHOU Yejian①②ZHANG Lei①②WANG Hongxian①②XING Mengdao①②NIU Wei③
①(,,’710071,)②(,,’710071,)③(,’710043,)
A new method for attitude estimation for space satellite targets is presented by extracting typical linear structures in ISAR imaging sequence and using information of target’s position in orbits to analyze the three-dimensional attitude of space satellite targets. With the analyzing process for space satellite targets’ geometric structures, the algorithm utilizes Radon transformation to realize the extraction of linear structures, like solar wings, planar antennas, in ISAR imaging sequences. After finishing the relevance of these linear structures among different frames, the angle information of typical linear structures in range-Doppler plane is extracted. At last, with target’s position information in orbits, a matrix sequence of the ISAR range-Doppler projection is acquired to estimate the three-dimensional attitude of linear structures, and realize exact solution of space satellite targets’ attitude. The simulation experiment result illustrates that the algorithm can realize the attitude estimation of typical units in space satellite targets, and the multistatic model algorithm shows its advantage in estimation accuracy.
Inverse SAR (ISAR) imaging; Geometrical projection matrix; Attitude estimation; Radon transform; Multistaic ISAR
TN957.52
A
1009-5896(2016)12-3182-07
10.11999/JEIT160603
2016-06-06;改回日期:2016-11-28;
2016-12-13
张磊 leizhang@xidian.edu.cn.
国家自然科学基金(61301280, 61301293)
The National Natural Science Foundation of China (61301280, 61301293)

