高分辨率机载InSAR高程距离向空变误差定标方法

洪 峻 曾友兵③ 王 宇



高分辨率机载InSAR高程距离向空变误差定标方法

洪 峻①②曾友兵*①②③王 宇①②

①(中国科学院电子学研究所 北京 100190)②(微波成像技术国家重点实验室 北京 100190)③(中国科学院大学 北京 100190)

高分辨率机载干涉合成孔径雷达(Interferometric Synthetic Aperture Radar, InSAR)是获取高精度数字高程模型(Digital Elevation Model, DEM)的重要手段之一。由于主副天线距离向相位方向图存在差异等原因，导致干涉相位偏差沿距离向变化，而传统的干涉定标方法将干涉相位偏差视为常数进行定标，无法消除干涉相位沿距离向变化的误差，因此使得定标后反演得到的高程存在距离向空变误差。针对该问题，该文提出一种单独将干涉相位偏差沿视角进行多项式拟合的定标方法。最后，利用一组机载实测数据对该方法加以验证，实验结果表明，该方法能有效地解决高分辨率机载InSAR高程测量距离向误差的空变问题。

干涉合成孔径雷达；高分辨率；干涉定标；高程距离向空变误差；干涉相位偏差

1 引言

机载干涉合成孔径雷达(InSAR)是近年来迅速发展起来的一种地表探测技术，它能够快速地获取大面积的数字高程模型(DEM)，具有测量精度高、作业灵活等优点，因而在地形测绘和地表形变监测等领域得到了广泛的应用[4,5]。目前，先进的高分辨率机载InSAR系统测高精度达到0.5 m以内[6,7]。系统干涉参数(基线长度，基线倾角，干涉相位等)偏差是限制InSAR高程测量精度的重要因素之一[8]，为提高系统高程测量精度，需通过InSAR定标来对这些系统干涉参数进行标定和校正。

机载InSAR通常采用基于敏感度方程的定标方法[9]，其基本原理是利用InSAR目标高程重建模型对各干涉参数的偏导建立参数偏差与高程偏差之间的关系，即敏感度方程，再通过一定数量的地面控制点(Ground Control Point, GCP)高程信息对敏感度方程进行求解，得到干涉参数偏差，进而对各干涉参数进行校正。目前，基于敏感度方程的定标方法中大多采用基线长度、基线倾角和干涉相位3个参数共同构建敏感度矩阵，同时对这3个参数偏差进行求解，本文中将该方法称为传统方法。传统方法存在两方面问题：(1)干涉相位与基线长度和基线倾角之间存在很强的相关性，对该3个参数求偏导共同构建敏感度方程使得定标模型本身不准确，同时敏感度矩阵条件数大，病态严重，影响求解结果精度[12]；(2)传统方法将干涉相位偏差视为常数，然而实际中，机载InSAR由于受到机身多路径反射误差[12,13]以及主副天线距离向相位方向图差异[14,15]等因素的影响，干涉相位偏差沿视角方向(即距离向)变化，在高分辨率条件下，该变化不可忽略。传统的定标方法将干涉相位偏差标定为一常数，无法消除沿距离向变化的相位误差，因此定标后的反演高程存在距离向空变误差。

针对高分辨率机载InSAR高程测量距离向误差空变问题，本文提出了一种改进的定标方法，结合传统的敏感度方程定标模型，选取基线长度和基线倾角两个参数构建敏感度方程，而将干涉相位偏差建模为视角的多项式函数，单独进行拟合，最终得到3个参数的定标结果。通过将干涉相位偏差从敏感度方程中分离出来并拟合成雷达视角的多项式函数单独进行求解，一方面减小了敏感度矩阵的条件数，降低矩阵病态程度，提高参数求解精度，另一方面能标定干涉相位沿距离向变化的偏差，解决InSAR高程测量距离向误差空变问题。最后，利用实际机载InSAR数据验证了该方法的有效性。该方法仅需一定数量沿距离向分布的地面控制点，具有简单实用、适用范围广的优点。

2 干涉相位偏差分析与建模

引起机载双天线InSAR系统干涉相位偏差沿距离向变化的因素主要有两个，一是机身多路径反射误差，二是主副天线距离向相位方向图差异。在机载双天线InSAR系统中，部分雷达回波经机身反射后进入天线，并与直接进入天线的雷达回波叠加在一起，该现象称为多路径反射[13]。经过机身反射后的雷达回波将引起干涉相位误差，不同的机载InSAR系统多路径误差强弱不等，有的系统多路径误差能引起米级的高程误差[16]。文献[12]和文献[13]都对多路径误差进行了详细的分析与建模，多路径误差数学模型可表示为

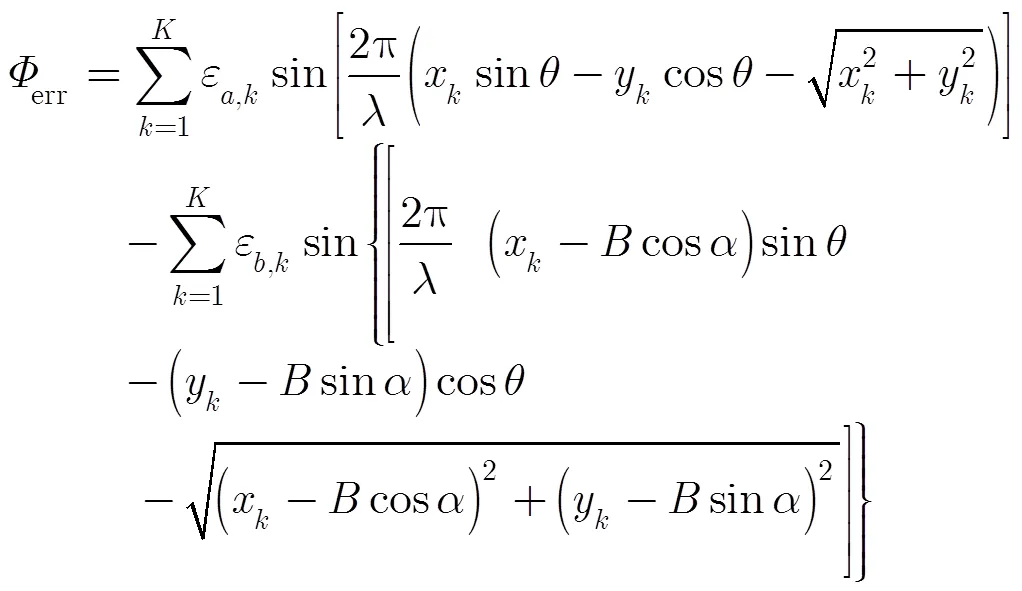
主副天线距离向相位方向图差异是引起干涉相位偏差沿距离向变化的另一个重要因素，机载双天线InSAR系统在设计研制过程中，主副天线距离向方向图可能存在一定差异，文献[14]给出了一部真实的双子孔径有源相控阵天线实测相位方向图，两天线相位差的变化量沿距离向可达0.06 rad以上，在InSAR中，该量级的干涉相位误差可引起分米级的高程误差。虽然前期可以在微波暗室中测量出主副天线相位方向图的差异，然而将天线安装至载机平台上后由天线安装误差以及天线罩相位特性差异引起的相位变化则无法事先测量。针对主副天线距离向相位方向图差异问题，文献[17]在MEMPHIS SAR数据处理中提出一种利用成交叉航线的机载实测数据来校正该误差的方法，以其中一条航线的数据为实验数据，另一条垂直航线的数据为参考数据，将实验数据距离向高程与参考数据方位向高程进行比较，得到由沿距离向相位误差引起的高程误差，进而对相位误差进行估计。最终的校正结果显示干涉相位误差沿距离向的变化量达0.1 rad。该方法需设计垂直交叉的航线，增加了飞行任务的难度和数据处理量。

根据以上分析可知，干涉相位偏差呈现沿雷达视角变化的特性，为了简化数据处理，同时又不失一般性，在本文中，将干涉相位偏差建模为视角的多项式函数，如式(2)所示。

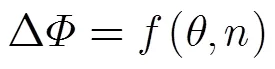
3 高程距离向空变误差定标方法

3.1 敏感度方程的构建

基于敏感度方程的定标是通过敏感度方程建立各干涉参数偏差与高程偏差之间的关系，通过求解方程组对各参数偏差进行估计，从而修正各干涉参数值。许多学者都对InSAR高程重建模型进行了研究[12,18]，如图1所示，,分别为主副天线相位中心位置，为大地坐标系，其中轴沿载机飞行方向，轴与轴垂直并水平向右，轴与轴，轴垂直并构成右手坐标系。为目标点位置，为主天线高度，为主天线到目标点的斜距，为载机平台速度，为主天线斜视角，为基线长度，为基线倾角，为斜视时下视角。由图1中的几何关系可得目标点的3维位置模型为

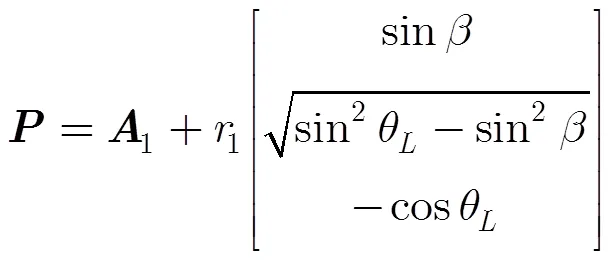
(4)

由式(5)可以看出，影响目标高程精度的系统参数主要包括基线长度，基线倾角和干涉相位等，传统的定标方法中同时利用这3个参数构建敏感度方程，使得敏感度矩阵条件数大，病态严重，影响了参数求解精度，同时敏感度方程中干涉相位偏差为常数，与实际情况不符，在高分辨率条件下，必须对沿距离向变化的干涉相位偏差进行标定。因此本文中只选取基线长度和基线倾角两个参数构建敏感度方程，而对干涉相位偏差单独进行多项式拟合。利用式(5)对,求偏导得

(6)

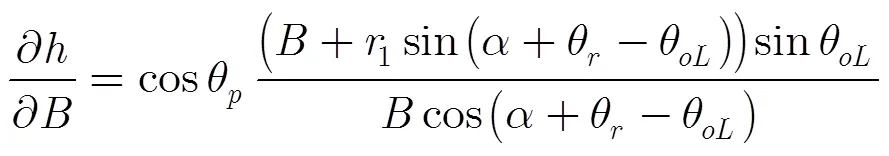
其中

(8)

此时敏感度矩阵为

式中行向量代表某一特定地面控制点位置处高程对各参数的偏导，代表选用的控制点数目。控制点高程偏差和干涉参数偏差之间的关系可表示为

(10)

通过求解敏感度方程式(10)的最小二乘解即可得到基线长度和基线倾角参数偏差值。

图1 干涉SAR几何示意图

3.2 敏感度矩阵条件数分析

敏感度矩阵条件数是影响干涉参数偏差求解精度的重要因素之一。矩阵的条件数定义为矩阵范数与矩阵逆范数的乘积[19]，即

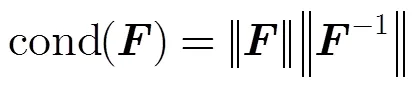
(12)

在控制点高程测量时，差分GPS测量仪器和方法会引入测量误差，因此高程偏差向量存在一定的误差，它将引起参数偏差解向量产生误差，假设的误差为，此时引起的参数偏差解向量误差为，根据敏感度方程式(10)有

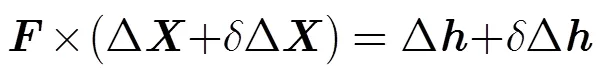
(14)

对式(14)取范数，得

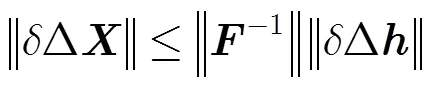
根据式(12)和式(15)可得

(16)

表1给出了传统方法利用基线长度、基线倾角和干涉相位3个参数构建敏感度矩阵和本文中仅利用基线长度和基线倾角两个参数构建敏感度矩阵的条件数数量级。由表可知，本文2参数组合方案的敏感度矩阵条件数量级仅为101，较传统方法的3参数组合方案下降了4个数量级，因此本文方法有利于提高干涉参数定标精度。

表1 敏感度矩阵条件数量级

敏感度矩阵参数组合条件数量级 传统方法3参数组合方案 本文提出的2参数组合方案

3.3定标算法总体流程

本文采用敏感度方程计算基线长度和基线倾角偏差，而干涉相位偏差则单独进行多项式拟合，为了同时标定这3个参数，采用敏感度方程和干涉相位偏差拟合交叉迭代的方式进行定标，具体步骤如下：

第1步 选择一定数量沿距离向分布的地面控制点，根据初始系统干涉参数计算各控制点的视角和干涉相位，并与InSAR测量得到的干涉相位作差的到每个控制点的干涉相位偏差，然后对干涉相位偏差进行多项式拟合，得到多项式各阶系数初始值；

第2步 利用拟合后的干涉相位偏差对整幅SAR图像的干涉相位进行校正；

第3步 利用敏感度方程求解基线长度和基线倾角偏差，并对参数进行校正；

第4步 更新干涉参数后计算各控制点的反演高程精度是否达到要求，若已满足精度要求，则获取前面的干涉参数定标结果，否则根据更新后的干涉参数重新计算GCP的视角和干涉相位偏差，并对干涉相位偏差进行多项式拟合，更新多项式各阶系数，并重复第2步至第4步的过程，直至反演高程精度满足要求。定标算法流程图如图2所示。

4 实际数据验证与结果分析

为了对本文方法的有效性进行验证，本文采用中国科学院电子学研究所机载双天线干涉SAR获取的一组实际数据进行试验，该InSAR工作在X波段，平面分辨率为，其系统主要参数如表2所示。图像获取时间为2014年9月30日，获取区域位于我国陕西省某地，地形以平地为主，图像范围内分布有道路、农田、水池和建筑物等。场景SAR图像如图3所示。

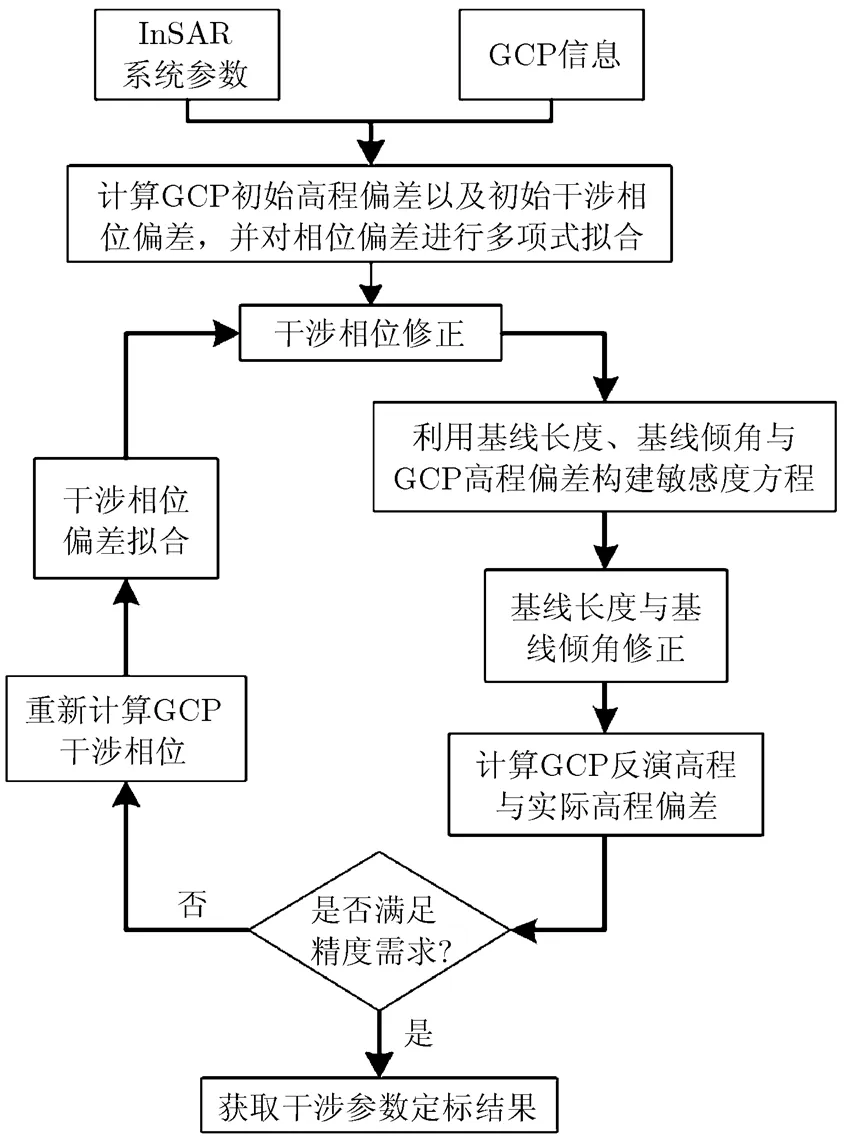
图2 定标算法流程图

表2 InSAR系统参数

实验中共采用5个沿距离向分布的地面控制点，每一控制点处均布设有角反射器，其坐标由差分GPS测量得到，高程精度优于5 cm，图3中白色方框标记出了各控制点在SAR图像中的分布情况。实验中采用二次多项式对干涉相位偏差进行拟合，具体的函数形式为

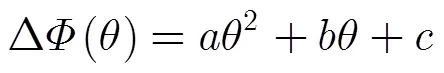
根据上节中的定标算法流程进行定标实验，最终得到各参数定标结果。干涉相位偏差的拟合结果如图4所示。由图4可以看出，经过两次迭代后，干涉相位偏差沿距离向的变化量在0.08 rad以内。迭代过程中干涉相位偏差拟合得到的二次多项式各阶系数值如表3所示。表4给出了传统方法和本文方法得到的基线长度和基线倾角参数定标结果。

表3干涉相位偏差拟合系数结果

参数abc 初始值0.0015-0.1442709.8767 第1次迭代-0.0438708.5141 第2次迭代-0.0428708.4945

表4基线长度与基线倾角定标结果

参数传统方法本文方法 基线长度(m)2.2150212.214508 基线倾角(rad)-0.002096-0.002208

为了验证本文方法能有效解决InSAR高程距离向空变误差问题，实验中选取了39个高程检查点，检查点坐标信息由陕西煤航信息产业有限公司野外实测得到。图5给出了由本文方法和传统方法定标后各检查点的高程误差情况，检查点1~39沿距离向从近距到远距分布。由图5(a)和图5 (b)可以看出，传统定标方法的结果在近距和远距检查点高程误差较中间区域明显增大，高程误差沿距离向呈现明显的空变特性，这说明传统的定标方法没有消除沿距离向变化的干涉相位误差。而利用本文方法所得的结果在近距和远距的检查点高程误差相对传统方法均明显减小，在整个测绘带宽内高程误差曲线较平缓，距离空变现象明显减弱。传统方法和本文方法检查点的均方根误差分别为0.4404 m和0.3045 m，本文方法较传统方法高程精度提高了10 cm以上。实验结果验证了本文方法的有效性。

图3 定标场SAR图像及控制点分布情况

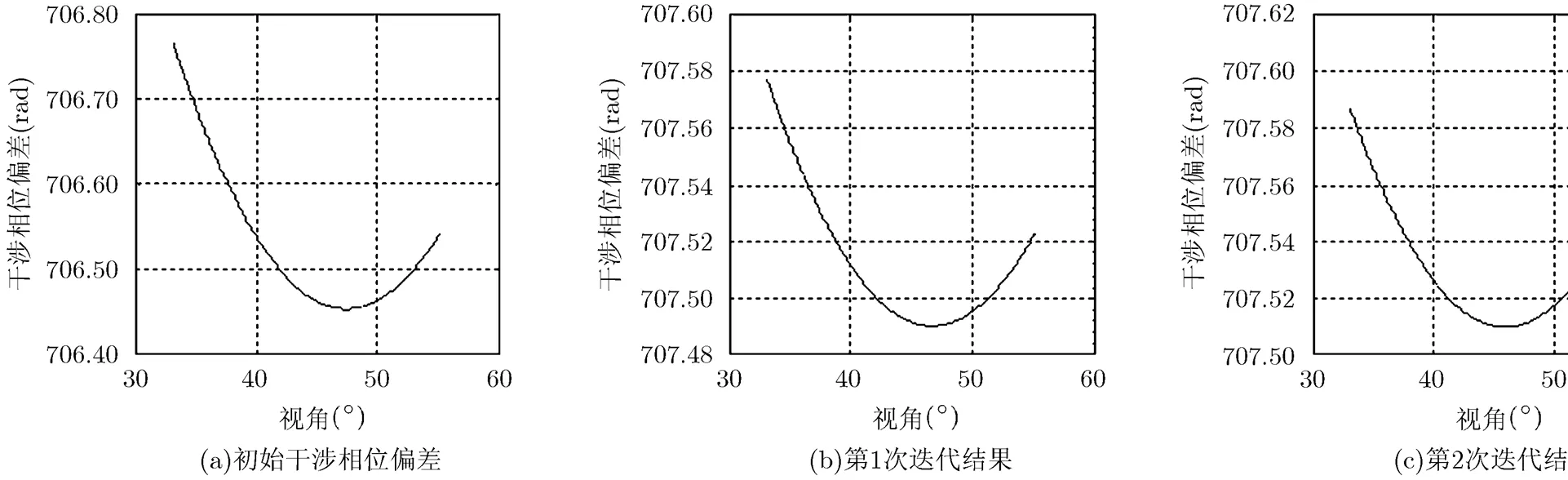
图4 干涉相位偏差拟合结果

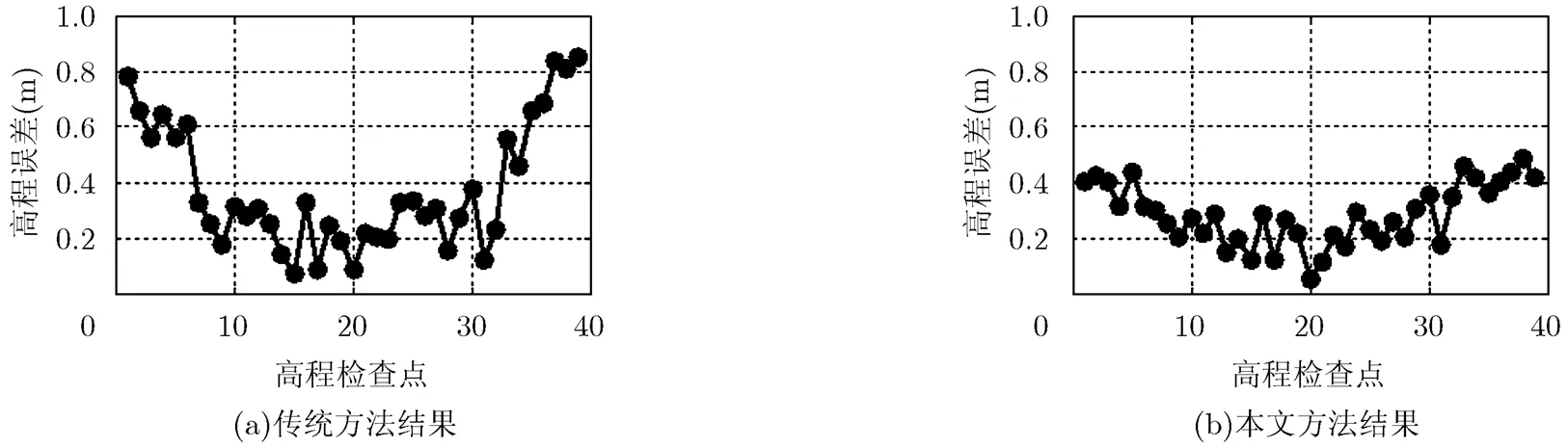
图5 高程检查点误差情况

5 结论

针对高分辨率机载InSAR高程测量距离向误差空变问题，本文提出了一种改进的定标方法，选取基线长度和基线倾角构建敏感度方程，而将干涉相位偏差建模为视角的多项式函数单独进行估算，通过地面控制点信息对这3个参数进行校正。经机载双天线InSAR系统获取的实际数据验证，与利用敏感度方程将干涉相位偏差标定为常数的传统定标方法相比，本文方法能较好地消除干涉相位沿距离向变化的偏差，可有效地解决机载InSAR高程测量距离向误差的空变问题。此外，本文中在整个距离向将干涉相位偏差拟合为二次多项式，当可用的控制点数量较多时，可沿距离向分段对干涉相位偏差进行多项式拟合，使干涉相位偏差定标结果更精确。

参考文献

[1] Kobayashi T, Umehara T, Uemoto J,Evaluation of digital elevation model generated by an airborne interferometric SAR (Pi-SAR2)[C]. IEEE International Geoscience and Remote Sensing Symposium, Quebec City, Canada, 2014: 378-381. doi:10.1109/IGARSS. 2014.6946437.

[2] PINHEIRO M, REIGBER A, SCHEIBER R,. DEM generation using large-baseline airborne InSAR[C]. European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1-4.

[3] 王萌萌, 黄国满, 罗新, 等. 基于点相位改正的机载干涉SAR定标算法[J]. 测绘科学, 2014, 39(4): 97-101.

WANG Mengmeng, HUANG Guoman, LUO Xin,Calibration method for airborne interferometric SAR based on point phase correction[J]., 2014, 39(4): 97-101.

[4] Paul A R, Scott H, Ian R J,Synthetic aperture radar interferometry[J]., 2000, 88(3): 333-382. doi: 10.1109/5.838084.

[5] ZHOU J, LI Z, HE X,Glacier thickness change mapping using InSAR methodology[J].&, 2014, 11(1): 44-48. doi: 10.1109/LGRS.2013. 2245854.

[6] DE MACEDO K A C, WIMMER C, and MOREIRA J R. Highly accurate and precise airborne single-pass interferometry for DEM generation over challenging terrain [C]. IEEE International Geoscience and Remote Sensing Symposium, Quebec City, Canada, 2014: 394-397.doi: 10.1109/IGARSS.2014.6946441.

[7] Jager M, Pinheiro M, Ponce O,A survey of novel airborne SAR signal processing techniques and applications for DLR’s F-SAR sensor[C]. International Radar Symposium (IRS), Dresden, Germany, 2015: 236-241.doi: 10.1109/IRS.2015.7226358.

[8] Mallorqui J J, Rosado I, and Bara M. Interferometric calibration for DEM enhancing and system characterization in single pass SAR interferometry[C]. IEEE International Geoscience and Remote Sensing Symposium, Sydney, Australia, 2001: 404-406.doi: 10.1109/IGARSS. 2001.976172.

[9] Mallorqui J J, Bara M, and Broquetas A. Sensitivity equations and calibration requirements on airborne interferometry[C]. IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 2000: 2739-2741.doi: 10.1109/IGARSS.2000.859699.

[10] 靳国旺, 张薇, 向茂生, 等, 一种机载双天线InSAR干涉定标新方法[J]. 测绘学报, 2010, 39(1): 76-81.

JIN Guowang, ZHANG Wei, XIANG Maosheng,A new calibration algorithm of interferometric parameters for dual- antenna airborne InSAR[J]., 2010, 39(1): 76-81.

[11] 云烨, 曾琪明, 焦健, 等. 基于参考DEM的机载InSAR定标方法[J]. 测绘学报, 2014, 43(1): 74-82.

YUN Ye, ZENG Qiming, JIAO Jian,Calibration of airborne interferometric SAR data based on reference DEM[J]., 2014, 43(1): 74-82.

[12] 张薇. 机载双天线干涉SAR定标方法研究[D]. [博士论文]. 中国科学院电子学研究所, 2009.

ZHANG Wei. Research on interferometric calibration method for airborne dual-antenna InSAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Acamedy of Science, 2009.

[13] 毛永飞. 机载双天线干涉SAR误差补偿与定标技术研究[D]. [博士论文], 中国科学院电子学研究所, 2012.

MAO Yongfei. Researh on compensation and calibration for airborne dual-Antenna interferometric SAR[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Acamedy of Sciences, 2012.

[14] 孙慧峰, 邓云凯, 雷宏, 等. SAR天线相位中心的分析及测量[J]. 中国科学院研究生院学报, 2012, 29(6): 793-798.

SUN Huifeng, DENG Yunkai, LEI Hong,Analysis and measurement of SAR antenna’s phase center[J]., 2012, 29(6): 793-798.

[15] BACHMANN M, SCHWERDT M, ALFONZO G C,. Phase pattern calibration for interferometric applications in spaceborne SAR systems[J]., 2013. http://dx.doi.org/10.1155/ 2013/284698.

[16] Mao Y F, Xiang M S, Wei L D,The mathematic model of multipath error in airborne interferometric SAR system[C]. IEEE Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 2010: 2904-2907.doi: 10.1109/IGARSS. 2010.5652255.

[17] Magnard C, Brehm T, and Essen H. Processing of MEMPHIS Ka-Band multibaseline interferometric SAR data: from raw data to digital surface models[J].,2014, 7(7): 2927-2941.doi: 10.1109/JSTARS.2014. 2315896.

[18] Mallorqui J J, Bara M, and Broquetas A. Calibration requirements for airborne SAR interferometry[C]. Proceedings of SPIE, Barcelona, Spain, 2000: 267-278.

[19] 程云鹏, 张凯院, 徐仲, 等. 矩阵论[M]. 西安: 西北工业大学出版社, 2013: 122-135.

CHENG Yunpeng, ZHANG Kaiyuan, XU Zhong,Matrix Theory[M]. Xi’an: Northwestern Polytechnical University Press, 2013: 122-135.

洪 峻： 男，1960年生，研究员，博士生导师，研究方向为SAR定标技术、机载SAR系统设计.

曾友兵： 男，1990年生，硕士生，研究方向为机载InSAR定标技术.

王 宇： 男，1976年生，副研究员，研究方向为机载SAR定标技术.

Calibration Method of Rang-variantHeight Errors in High Resolution Airborne InSAR

HONG Jun①②ZENG Youbing①②③WANG Yu①②

①(,,100190,)②(,100190,)③(,100190,)

High resolution airborne Interferometric Synthetic Aperture Radar (InSAR) is one of the important methods to generate high precision Digital Elevation Model (DEM). Due to the phase pattern difference between the two antennas, the interferometric phase bias varies with the range. The traditional interferometric calibration regards the phase bias as a constant, and it is not able to correct the range-variant phase errors. Therefore, there arerange-variant errors of the reconstructed elevation. To solve this problem, this paper presents a calibration method that uses polynomial to fit the interference phase bias. At last, a set of real airborne InSAR data are used to validate the method, and the experimental results show that the proposed method can solve the problem of range-variantheight errors in high resolution airborne InSAR effectively.

InSAR; High resolution; Interferometric calibration; Range-variant height errors; Interferometric phase bias

TN959.73

A

1009-5896(2016)12-3245-07

10.11999/JEIT160021

2016-01-08；改回日期：2016-05-20；

2016-07-19

曾友兵 zengyoubing91@foxmail.com

对地观测系统重大专项(GFZX0403220402, GFZX 04032204)

The National Science and Technology Major Project (GFZX0403220402, GFZX04032204)