干扰子空间正交投影快速零陷跟踪波束赋形算法

马晓峰 陆 乐 盛卫星 韩玉兵 张仁李



干扰子空间正交投影快速零陷跟踪波束赋形算法

马晓峰*陆 乐 盛卫星 韩玉兵 张仁李

(南京理工大学电子工程与光电技术学院 南京 210094)

该文针对LEO星载阵列天线抑制角度动态变化的有源干扰的需要，提出一种干扰子空间正交投影的快速零陷跟踪波束赋形优化算法。算法采用干扰子空间动态更新与迭代正交投影，不断快速修正零陷位置，并通过迭代傅里叶变换(IFT)技术进行优化加速。所提出的快速算法在整个干扰零陷跟踪过程中，具有稳健和精确的控制方向图主瓣赋形区形状和阵元电流激励系数动态范围的能力，同时具备自适应最小化方向图旁瓣电平的能力，适用于星载系统在线实时计算。仿真实验验证了算法的快速性、有效性和稳健性。

低轨道卫星通信；快速波束赋形；抗干扰零陷；快速傅里叶变换

1 引言

低轨道(LEO)卫星通信多波束数字阵列天线不仅可以同时形成多个对地等通量覆盖的低旁瓣赋形波束，实现大张角覆盖区域的等灵敏度通信，还具备通信过程中实时调整方向图零陷位置，动态抑制干扰的能力。而稳健的快速波束赋形算法仍然制约着上述功能的在星载平台上的实现。

最早的波束赋形方法是Woodward-Lawson方法[1]，该方法旁瓣电平和通带内波纹控制困难。将Taylor或者 Chebyshev分布作为阵列孔径电流分布可以解决上述问题，但是天线必须是圆形或者矩形结构。近来，智能优化算法已经应用于天线综合问题，如遗传算法[2]、模拟退火算法[3]和粒子群算法[4]等。这些全局优化算法优化大型阵列时粒子数量巨大，计算量巨大，且收敛速度不确定。交替投影(AP)算法是一种非常有效且灵活的优化任意天线阵列结构阵元电流激励的方法，可实现方向图的精细控制[5]。最小均方误差(LMS)和加权最小均方误差(WLMS)方法也相继提出[6, 7]，可以调整每个角度在方向图逼近过程中的权重。文献[8]提出了交替投影和约束加权最小均方误差方法(CWLMS)，并给出该优化问题的近端分裂求解算法，有效处理阵元电流激励幅度和相位存在约束的问题。文献[9]在波束赋形过程中修正阵元间互耦，得到了很好的赋形效果。然而，上述算法虽然性能优越，但运算量都比较大，收敛速度和稳健性很难保证，且优化参数调整复杂，一般应用于离线静态波束方向图的优化，无法直接应用于大型数字阵列的在线实时计算。

对于LEO卫星通信系统，当存在较强的有源干扰时，除了覆盖该角度区域的赋形波束无法工作外，干扰从其他波束的旁瓣进入，也可能导致该波束无法正常工作。为了解决上述问题，需要在快速定位干扰源位置的前提下快速形成较深零陷，实现强干扰的空域抑制，并根据卫星运行轨道，动态调整方向图的零点位置。文献[10]提出了一种通过带约束的激励系数逼近作为优化代价函数的波束赋形方法，具有可选择增益覆盖和指定位置生成干扰零陷的能力。文章仅考虑满足约束方向的增益或者零陷要求，整个赋形区域的波动度很难控制，同时缺乏对旁瓣电平的有效控制。文献[11]针对任意结构的阵列天线进行方向图综合，要求在生成干扰零陷的同时控制激励系数幅度的动态范围(DRR)，最大化阵列效率[12, 13]。文章构造了干扰零空间子集和DRR子集，求解采用与文献[5]类似的子集间交替投影得到。算法在迭代过程中仅关心零陷的生成和DRR条件的满足，而对主瓣覆盖区域的形状和旁瓣电平都缺乏有效控制。上述零陷方向图赋形算法的运算速度和稳定性均不够理想。近年来，部分学者利用阵列天线阵元激励电流和远场方向图阵因子之间满足傅里叶变换对的关系，采用快速傅里叶变换(FFT)和快速傅里叶逆变换(IFFT)来进行算法加速。文献[14]应用迭代傅里叶变换(Iterative Fourier Technique, IFT)技术对大型平面天线进行快速低旁瓣综合，随后又把IFT技术应用到了稀疏直线阵[15]和大型稀疏平面阵[16, 17]的方向图综合中来。

本文针对LEO星载阵列天线抑制角度动态变化的有源干扰的需要，借鉴文献[5]和文献[11]子集投影的思想，以及文献[14]方向图综合IFT加速技术，提出了一种干扰子空间正交投影的快速零陷跟踪波束赋形优化算法。算法采用干扰子空间动态更新与迭代正交投影，快速修正零陷位置，避免干扰位置出现扰动时的输出性能下降问题[18]。所提出的快速算法在整个干扰零陷跟踪过程中，具有稳健和精确控制方向图赋形区形状和阵元电流激励系数DRR的能力，同时具备自适应最小化旁瓣电平的功能，适用于星载系统在线实时计算。

2 问题方程

2.1 阵列模型

其中，阵因子可以表示为

2.1.1矩形栅格阵列 矩形栅格阵列和轴方向阵元数为和，间距为和，式(2)可改写为

2.1.2三角栅格阵列 可以通过坐标伸缩和旋转变换将三角栅格阵列转换成行列阵元间距相等的矩形栅格阵列，伸缩和旋转过程如图1所示。图1以LEO星载阵列天线常用的等边三角栅格六边形阵列为例给出变换过程，灰色阵元为虚拟阵元(实际阵列没有这些阵元)。假设图1(a)中任意阵元初始坐标为；首先，对坐标进行伸缩变换，轴方向伸缩为原来的倍，轴方向伸缩为原来的倍，那么伸缩后的坐标变为，如图1(b)所示；接着，将坐标以原点为中心逆时针旋转度，则此时坐标变为，如图1(c)所示。将上述变换写成矩阵的形式则可表示为

所以三角栅格阵列的阵因子可以表示为

可见，三角栅格阵因子也可表示为2维离散傅里叶变换的标准的形式，不同的是其中。需要注意的是，对三角栅格结构的阵列天线来说，其阵元经过伸缩、旋转等变换转化成矩形栅格之后阵元间距并不等于原三角栅格的阵元间距。

综上所述，对于均匀阵元间距的矩形栅格平面阵列或三角栅格平面阵列，都可以建立阵元电流激励系数和阵因子之间的傅里叶变换关系，通过IFFT和FFT实现两者之间的快速转换。

2.2约束子集投影模型

由上述分析可以知道，阵因子与复电流激励系数之间满足2维离散傅里叶变化关系，可以通过IFT，在两者间进行转换。本文快速波束赋形就是在交替迭代过程中依次对期望的阵列阵因子和电流激励系数进行调整。调整可以采用子集投影模型表示。

2.2.1期望阵因子修正投影 每次迭代，电流激励系数经过式(7)的IFFT处理后得到的阵因子需要进行修正后作为期望阵列阵因子，可以定义阵因子修正投影算子如式(8)：

2.2.2干扰子空间正交投影 定义干扰子空间正交投影算子如式(9)：

电流激励系数经过干扰子空间正交投影处理后，可以确保阵因子在干扰角度位置产生较深零陷。

2.2.3电流激励系数动态范围修正投影 激励系数动态范围修正的目的是为了保证赋形效果和干扰有效零陷生成的同时，兼顾阵列效率和阵元间互耦对方向图的影响。定义电流激励系数向量的动态范围(DRR)为

需要指出，当电流激励系数相位动态范围需要约束，或者当应用于相控阵系统，幅度和相位为离散值的情况下，也可以采用式(13)类似方法定义相应的修正算子。

3 赋形优化算法

3.1 算法流程

算法的输入参数包括：方向图赋形区等通量特性及其允许波动度、电流激励系数的DRR、干扰是否存在以及干扰存在情况下实时变化的干扰位置。算法初始的激励系数可以是已经优化完成或者部分优化的静态电流激励系数，也可以是指向某个角度的阵列导向性矢量。本文提出的快速零陷跟踪波束赋形算法，本质上是利用高效IFT技术和子集投影技术迭代求解3个子集的交集。算法具体的执行步骤为：

步骤1 分析等间距平面阵列天线的阵列结构，确定矩形栅格阵列的伸缩变换矩阵和变换后阵元间距或者三角栅格阵列的伸缩变换矩阵，旋转矩阵和变换后阵元间距。

步骤4 根据赋形方向图的需要，确定可见区内方向图的赋形区、旁瓣区和过渡区(具体划分参考3.2节)。根据式(8)修正阵因子赋形区特性，旁瓣区均设置为0。

步骤6 当存在干扰时，根据式(9)，将电流激励系数投影到干扰正交空间，迭代过程中干扰正交空间根据干扰位置的变化动态调整变化。如果不存在干扰则直接进入步骤7。

不存在干扰情况下，本文算法逐次迭代可以快速逼近所需的赋形区特性和激励系数动态范围要求，获得优化的旁瓣电平；存在干扰的情况下，方向图零陷可以精确跟踪干扰，且跟踪过程中有效控制赋形区特性和激励系数动态范围，由于干扰位置在相邻两次迭代之间仅细微变化，方向图控制的稳健性强，旁瓣电平也不断动态优化，方向图性能优越。另外，算法步骤6和步骤7可以根据需要调整顺序，当需要严格控制激励系数动态范围时采用本文给出的步骤，当需要严格控制零陷误差时可以交换两个步骤。由于个别阵元激励系数幅度的调整对干扰零陷位置和深度的影响不大，步骤6和步骤7的顺序对算法性能影响不大。

3.2可见空间分析

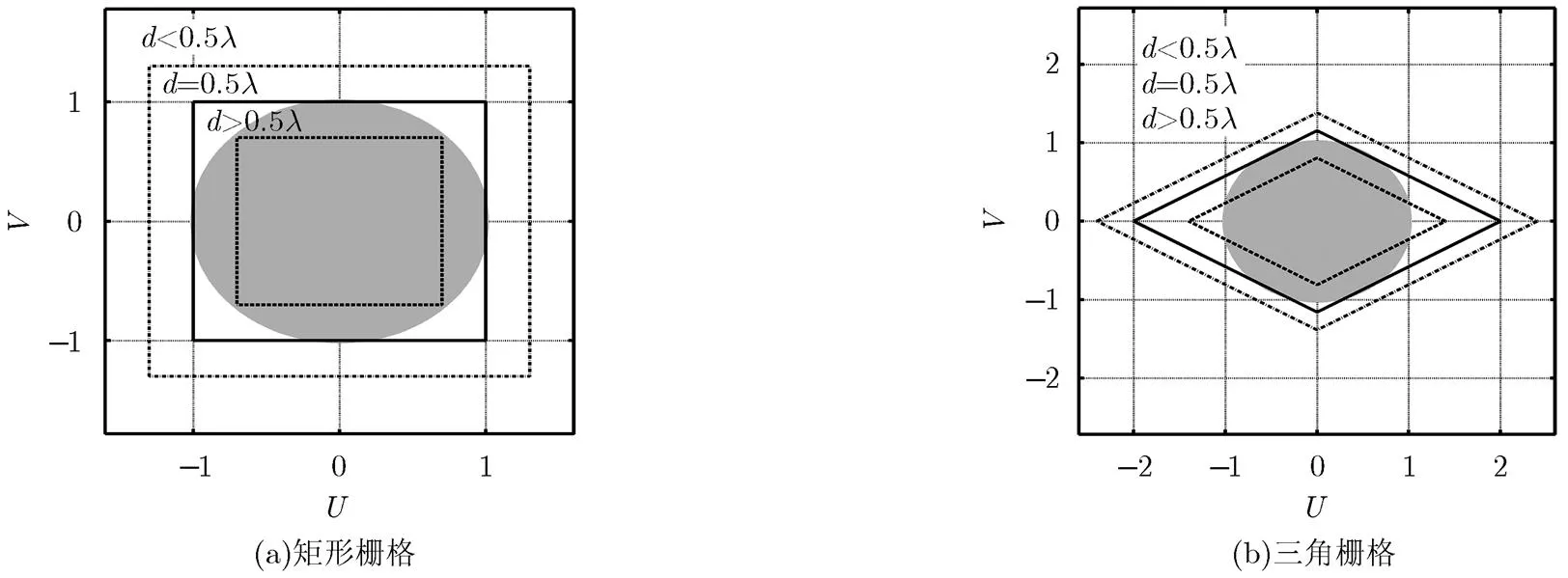
图2 阵列可见空间示意

对于行列阵元间距相等的矩形栅格阵列。图2(a)给出了3种典型阵元间距的情况下空间内阵因子方向图主周期所覆盖的情况。当时，2维IFFT变换得到的阵因子覆盖区域正好和可见空间对应圆相切；当时，覆盖区域大于可见空间的范围；当时，覆盖区域小于可见空间的范围，此时，可见空间没有完全覆盖，如果赋形波束的主瓣落在此阵因子覆盖区域的边界位置，会出现栅瓣。对三角栅格阵列来说，其阵元结构可以经过伸缩、旋转变换转化成矩形栅格阵列来考虑。以图1中等边三角栅格平面阵列为例加以说明，此时，对应的,,,。图2(b)画出了三角栅格情况下，3种典型阵元间距的情况下空间内阵因子方向图主周期所覆盖的情况。可以看出，与矩形栅格阵列类似，只是当时，未覆盖的可见区域位置不同。

4 仿真分析

本节将以文献[10]全球星移动卫星通信系统类似的91阵元三角栅格阵列结构为例，针对对地等通量覆盖和电流激励系数控制的需求，从静态方向图和动态干扰零陷方向图优化两方面开展快速算法的仿真和性能分析。假设单元天线为各向同性的全向天线，阵元间距为，阵列天线对地波束赋形覆盖采用3圈16个波束的结构，如图3所示，中心波束覆盖俯仰的范围，第2圈6个波束覆盖俯仰的范围，第3圈9个波束覆盖俯仰的范围。图4为轨道高度低轨道卫星系统，以俯仰增益需求归一化基准的等通量增益曲线，可以看到，增益需求大概相差，俯仰角越大对天线增益的要求越高。

图3 赋形波束赋形区覆盖示意图

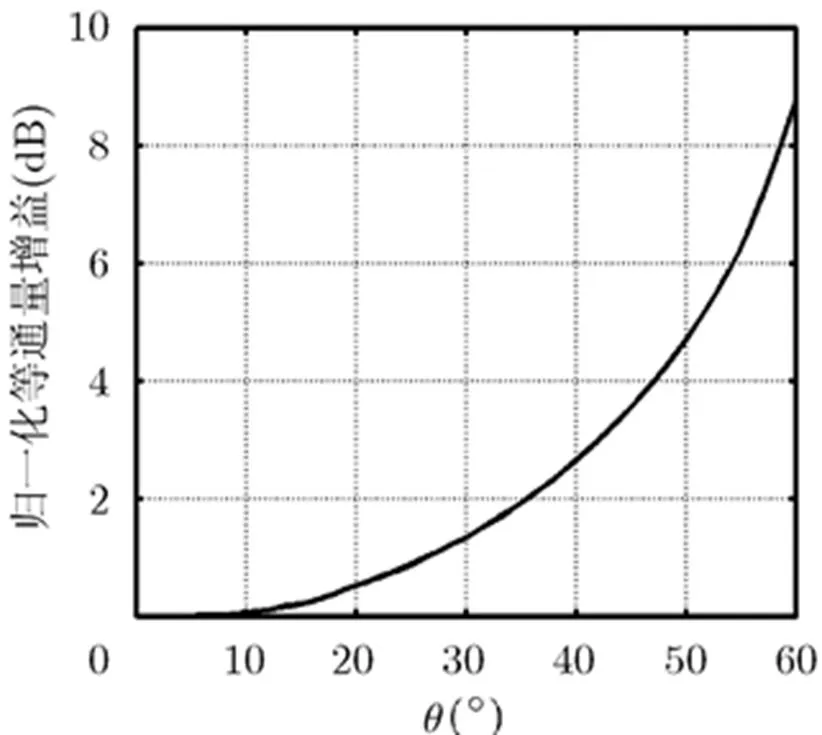
图4 归一化等通量增益曲线

仿真1 静态方向图优化性能仿真

本仿真以内圈2号波束的静态方向图赋形为例，分析迭代优化过程中收敛特性和主要参数的变化情况。设初始激励系数为波束指向时的导向性矢量，DRR设为10。图5给出了采用本文提出算法以及文献[8]交替投影(AP)算法，优化过程中激励系数的收敛曲线、赋形区增益变化曲线(即满足等通量增益覆盖条件下的最大角度处的增益)和旁瓣电平变化曲线，从这些曲线可以看出，本文算法迭代30次后，赋形性能已经可以满足要求，迭代约50次后波束方向图性能稳定，此时主瓣增益约，旁瓣电平接近。本文算法的优化性能和收敛特性均略优于AP算法。

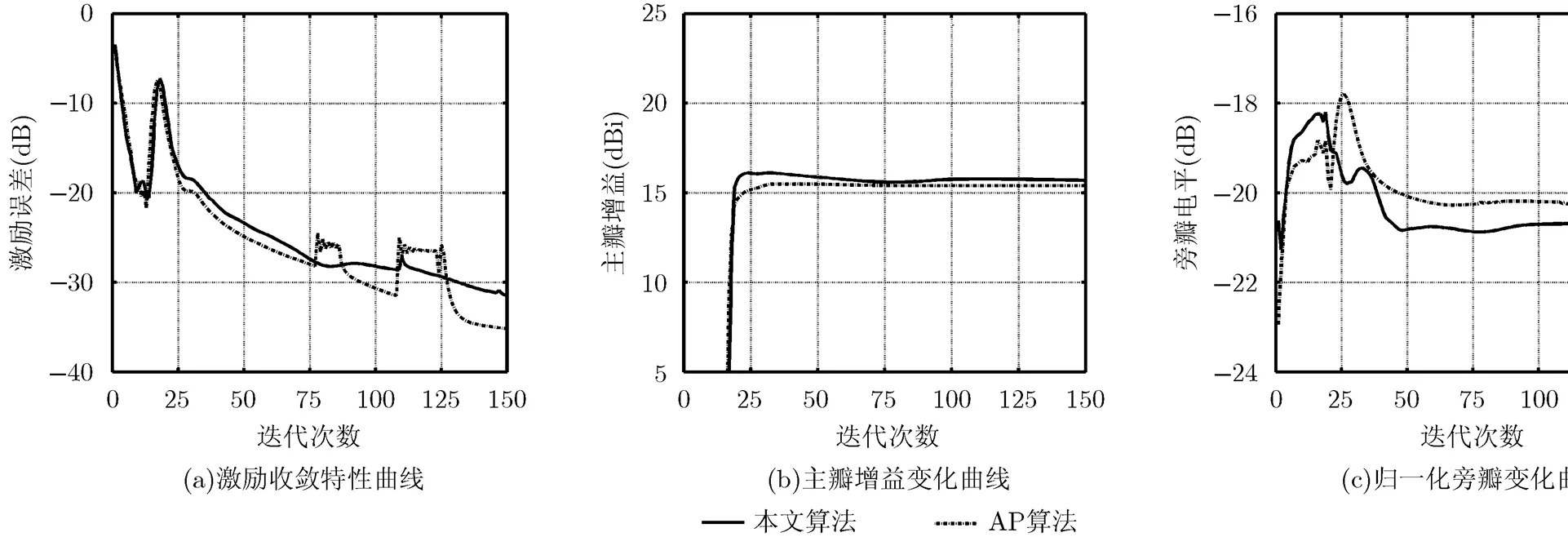
图5 对2号波束赋形时主要参数变化曲线

接着进行本文算法与AP算法在运算量方面的比较。本文算法是通过2维IFFT计算阵因子方向图的，可以假设方向图空间采样点数为，其中赋形区的采样点数为(一般), AP算法在整个可见空间的采样点数为，阵列天线阵元总数为，为了方便比较设。表1给出了两种算法一次迭代过程的运算量分析，其中表示个复数开根号的乘法运算量，可以看出当较大时，本文算法在计算量方面优势明显。以上述91阵元矩形栅格阵列和2号波束赋形为例，当空间采样点数相等，在配备Intel Core-i3 M380处理器的PC上，MATLAB仿真完成本文算法一次迭代所用时间为，而完成AP算法一次迭代所用时间为。本文算法运算量仅为AP算法的。

表1本文算法与文献[8]AP算法单次迭代需要的运算量分析表

仿真2 DRR的设置对旁瓣电平和主瓣增益的影响仿真

本文在期望阵因子修正过程中直接将旁瓣区电平均设为0，有效降低了运算量，还可以获得该形状赋形波束在固定激励系数DRR下的最优旁瓣电平。图6给出了不同激励系数DRR情况下，1号，2号和8号赋形波束最终优化得到的旁瓣电平和赋形区最大角度处的增益。可以看出，优化后的旁瓣电平都随DRR的增大而减小，当DRR取值为10左右，旁瓣电平和主瓣增益均可以达到较优值，一味增大DRR，旁瓣电平降低有限，同时还会影响主瓣增益。另外，主瓣宽度越宽，优化得到的旁瓣电平越低。当DRR为10时，波束1最终能实现的旁瓣电平在左右，主瓣增益在左右，波束2的旁瓣电平在左右，主瓣增益左右，而波束8的旁瓣电平在左右，主瓣增益可达到以上。较好地满足等通量需求。

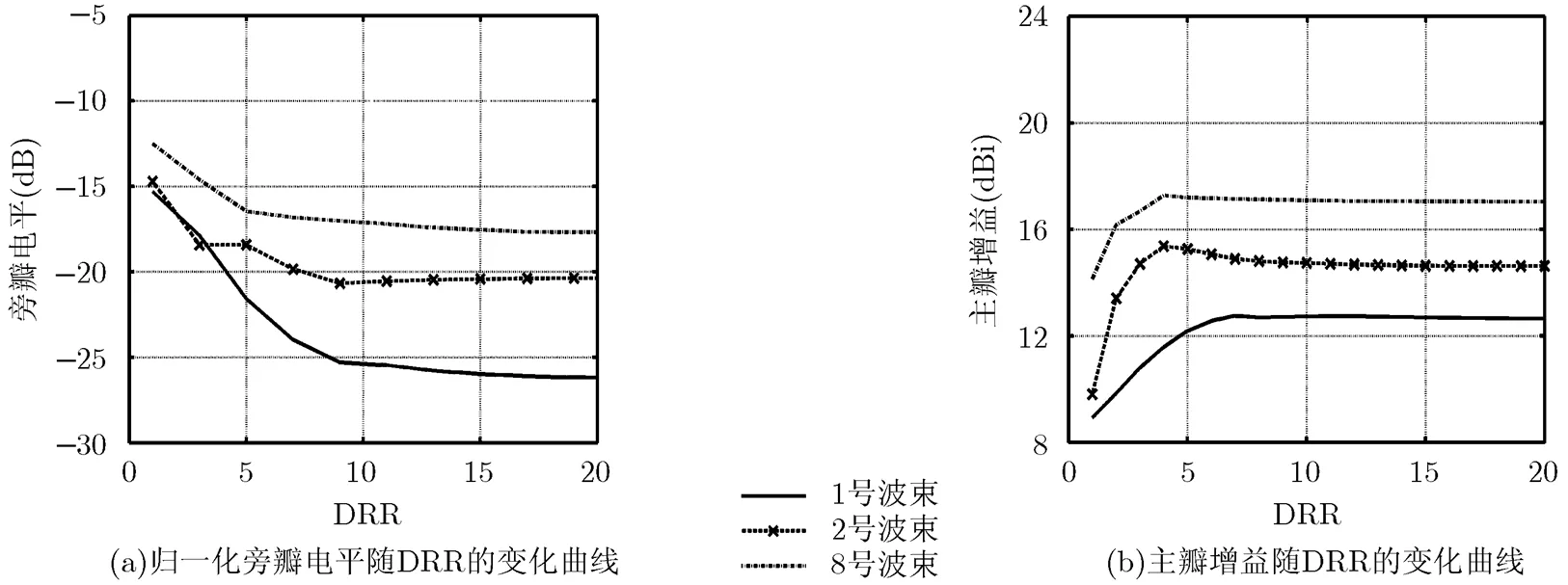
图6 归一化旁瓣电平和主瓣增益随DRR的变化曲线

仿真3 零陷跟踪性能仿真

本仿真主要开展干扰位置动态变化过程中，快速算法零陷跟踪性能的仿真与分析。仿真以2号波束为例，给出干扰角度变化率，干扰位置从俯仰角动态变换过程中，赋形波束动态方向图的性能。假设每次迭代需要时间为，则每次迭代干扰角度变化，仿真以4.1节优化得到的静态波束方向图的激励系数为初始值。

图7分别画出了最低零陷跟踪误差、赋形区最大角度增益和旁瓣电平随干扰位置的变化曲线。可以看出，干扰在进入和移出主波束时最低零陷角度误差较大，而干扰完全进入主波束时角度误差很小，但由于零陷区范围较大，该误差对干扰抑制的影响很小；存在干扰情况下赋形区最大角度增益优于不存在干扰的静态方向图，特别是当干扰完全进入赋形区时增益最高，说明干扰的存在，特别是进入赋形区后，由于零陷生成将能量挤压至剩余的赋形区和过渡区，赋形区增益得到提升；同最低零陷角度误差一样，赋形波束旁瓣电平也在干扰完全进入赋形区时出现最低值，这也与赋形区增益提升有一定的关系。

图7 动态干扰抑制过程中各参数随干扰位置变化曲线

图8为干扰动态运动至几个典型位置时，得到的该时刻(仅该时刻一次迭代的结果)的2号波束3维俯视方向图。可以看到在方向图赋形区和旁瓣电平有效控制的前提下，抗干扰零陷可以有效生成。

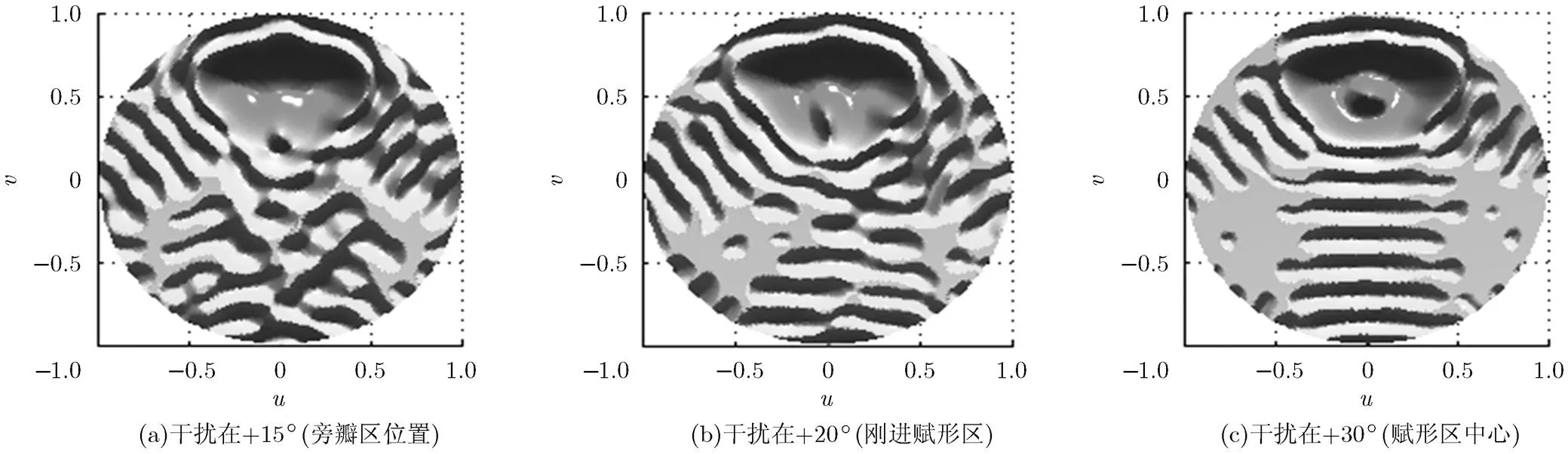
图8 干扰动态运动至几个典型位置时的2号波束3维俯视方向图

5 结束语

该文针对LEO星载阵列天线抑制角度动态变化的有源干扰的需要，提出了一种干扰子空间正交投影的快速零陷跟踪波束赋形优化算法。算法利用IFT技术加速，采用迭代子集投影技术求解3个子集交集，得到阵列电流激励系数的优化值。迭代过程中参数动态调整，确保满足方向图赋形区特性、阵列效率和零陷跟踪要求的前提下，得到较低旁瓣。仿真结果表明，采用本文算法进行方向图赋形，具有方向图优化性能好，速度快，方向图稳定性强，旁瓣电平低的特点。但算法针对干扰子空间变化的收敛特性还有待进一步分析，另外，在给定DRR下的最优旁瓣电平以及给定旁瓣电平情况下的最优DRR有待进一步分析。

参考文献

[1] BALANIS CA. Antenna Theory: Analysis and Design (3rd ed)[M]. New York, NY, USA: Wiley, 2005: 399-405.

[2] BOERINGER D W and WERNER D H.Particle swarm optimization versus genetic algorithms for phased array synthesis[J].2004, 52(3): 771-779.doi:10.1109/TAP. 2004.825102.

[3] FERREIRA J A and ARES F. Pattern synthesis of conformal arrays by the simulated annealing technique[J]., 1997, 33(14):1187-1189. doi:10.1049/el:19970838.

[4] ROBINSON J and RAHMAT-SAMII Y. Particle swarm optimization in electromagnetics[J].,2004,52(2):397-407. doi:10.1109/TAP.2004.823969.

[5] BUCCIOM, ELIAGD, and ROMITOG.Power synthesis of conformal arrays by a generalized projection method[J].,, 1995, 142(6): 467-471. doi:10.1049/ip-map:19952290.

[6] VASKELAINEN L I. Iterative least-squares synthesis methods for conformal array antennas with optimized polarization and frequency properties[J].,1997, 45(7): 1179-1185. doi:10.1109/8.596912.

[7] HADDADI A, GHORBANI A, and RASHED-MOHASSEL J. Cosecant-squared pattern synthesis using a weighted alternating reverse projection method[J].and, 2011, 5(15):1789-1795. doi:10.1049/iet-map.2011.0056.

[8] HAN Y, WAN C, SHENG W,. Array synthesis using weighted alternating projection and proximal splitting[J]., 2015, 14: 1006-1009. doi:10.1109/LAWP.2015.2389804.

[9] 龚树凤, 贲德, 潘明海, 等. 考虑互耦修正的机会阵雷达波束方向图综合优化[J]. 电子与信息学报, 2014, 36(3): 516-522. doi:10.3724/SP.J.1146.2013.00108.

GONG S,BEN D, PAN M,. Beam pattern synthesis optimization for opportunistic array radar with mutual coupling[J].&, 2014, 36(3): 516-522. doi:10.3724/SP.J.1146.2013.00108.

[10] YU KB. Adaptive beamforming for satellite communication with selective earth coverage and jammer nulling capability[J].,1996,44(12):3162-3166. doi:10.1109/78.553494.

[11] ROBERTO V. Consistency of constraints on nulls and on dynamic range ratio in pattern synthesis for antenna arrays[J].,2007,55(10):2662-2670. doi:10.1109/TAP.2007.905828.

[12] 宋海伟, 洪春冲, 李文魁, 等. 星载多波束阵列天线中单元失效分析[J]. 航天电子对抗, 2015, 31(5): 9-12. doi:10.3969/ j.issn.1673-2421.2015.05.003.

SONG H, HONG C, LI W,. Analysis of element failure in space-borne multibeam array antenne[J]., 2015, 31(5): 9-12. doi:10.3969/j.issn. 1673-2421.2015.05.003.

[13] 刘晓莉, 廖桂生, 曾操. 最大化阵列效率的方向图综合方法[J]. 西安电子科技大学学报, 2009, 36(5): 807-812. doi:10.3969/ j.issn.1001-2400.2009.05.009.

LIU X, LIAO G, and ZENG C. Pattern synthesis method for array efficiency maximization[J]., 2009,36(5):807-812. doi:10.3969/j.issn. 1001-2400.2009.05.009.

[14] KEIZER WPMN. Fast low-sidelobe synthesis for large planar array antennas utilizing successive fast fourier transforms of the array factor[J].,2007, 55(3):715-722. doi:10.1109/TAP.2007.891511.

[15] KEIZER WPMN. Linear array thinning using iterative FFT techniques[J].,2008, 56(8): 2757-2760. doi:10.1109/TAP.2008. 927580.

[16] KEIZERWPMN.Large planar array thinning using iterative FFT techniques[J].,2009, 57(10): 3359-3362. doi:10.1109/TAP. 2009.2029382.

[17] KEIZER WPMN. Synthesis of thinned planar circular and square arrays using density tapering[J].,2014, 62(4): 1555-1563. doi:10.1109/TAP.2013.2267194.

[18] 李文兴, 毛晓军, 孙亚秀. 一种新的波束形成零陷展宽算法[J]. 电子与信息学报, 2014, 36(12): 2882-2888. doi:10.3724/SP.J. 1146.2013.02018.

LI W, MAO X, and SUN Y. A new algorithm for null broadening beamforming[J].&, 2014, 36(12): 2882-2888. doi:10.3724/SP.J.1146.2013.02018.

Fast Nulls Tracking Pattern Synthesis Based on Jammer Subspace Orthogonal Projection

MA Xiaofeng LU Le SHENG Weixing HAN Yubing ZHANG Renli

(,&,210094,)

A fast nulls tracking pattern synthesis algorithm based on jammer subspace orthogonal projection is proposed, which can suppress the dynamic active jamming for LEO spaceborne array antenna. The algorithm corrects the nulls positions of radiation pattern synchronously through dynamically jammer subspace updating and iterative orthogonal projection, while the Iterative Fourier Transform (IFT) technique is adopted to accelerate the correction. The proposed algorithm can maintain the mainlobe region and control the dynamic range ratio of excitations robustly and precisely, while minimizing the pattern sidelobe adaptively, so it is suitable for online real-time calculation in spaceborne array antenna. Simulation results verify the rapidity, effectiveness, and robustness of the proposed algorithm.

Low Earth Orbit (LEO) satellite communication; Fast pattern synthesis; Anti-jamming nulls; Fast Fourier Transform (FFT)

TN 927; TN821+.91

A

1009-5896(2016)10-2560-08

10.11999/JEIT151438

2015-12-17；改回日期：2016-05-16；网络出版：2016-07-04

马晓峰 maxiaofeng@njust.edu.cn

国家自然科学基金(61501240, 11273017)，上海航天基金重点项目(SAST201437)

The National Natural Science Foundation of China (61501240, 11273017), The Key Project of Shanghai Aerospace Foundation of China (SAST201437)

马晓峰： 男，1981年生，讲师，研究方向为阵列信号处理与雷达信号处理.

陆 乐： 女，1992年生，硕士生，研究方向为数字波束形成与波束赋形.

盛卫星： 男，1966年生，教授，博士生导师，研究方向为阵列信号处理、雷达信号处理与雷达成像等.

韩玉兵： 男，1972年生，副教授，博士生导师，研究方向为图像处理、阵列信号处理等.

张仁李： 男，1986年生，讲师，研究方向为雷达信号处理等.