基于投影空间重构的小信号波束形成

谢少彪，倪涛

（1.上海航天技术研究院上海201109；2.上海卫星工程研究院上海200240）

基于投影空间重构的小信号波束形成

谢少彪1，倪涛2

（1.上海航天技术研究院上海201109；2.上海卫星工程研究院上海200240）

针对基于特征空间（Eigen Space_Based A1gorithm）的自适应波束形成算法在小信号条件下会出现的主瓣偏移，波束畸变，输出性能急剧下降的现象，提出了一种投影子空间重构的方法。该方法利用噪声在时间上不相关的特性，对投影空间进行重构，在此过程中削弱噪声能量，从而有效维持信号、噪声子空间的正交性，改善了传统EBS算法在低信噪比下的性能。实际计算机仿真结果表明了本文算法的有效性和优越性。

小信号；波束畸变；波束形成；特征空间；投影空间重构

自适应波束形成技术是阵列信号处理中一个重要分支，它能够根据实际环境变化，实时调整权值来降低阵列误差的对波束形成性能的影响，具有相当广泛的应用前景。采样矩阵求逆算法（Samp1e Matrix Inversion）是最常用的自适应波束形成算法，该算法收敛速度快，易于实现。但是SMI在少快拍，高信噪比条件下会导致主瓣偏移，波束畸变，输出SINR下降。为了弥补SMI的缺陷，出现了很多新的算法，其中包括最为常见的对角加载算法［1_2］和子空间投影算法［3_4］。

对角加载通过对Capon最小方差问题进行正则化处理，相当于给阵列采样协方差矩阵加上一个对角阵，从而减弱小特征值对应的噪声波束的影响，抑制波束图畸变。文献［5_7］对对角加载算法进行了优化改进，但是这些算法并没有给出加载因子的严格标准，存在局限性，不能广泛适用。特征空间法是将最优权值向信号子空间投影，摒弃噪声空间的分量。该算法因具有较快的收敛速度和较强的稳健性，也出现了很多改进算法。文献［8_10］通过对来波方向进行重新估算来加强算法稳定性。文献［11］利用矢量旋转方法对预定导向矢量进行校正。文献［12］为降低算法运算量，利用协方差矩阵的高次幂来逼近信号空间。文献［13_15］使用Forward_Backward法对协方差矩阵进行重构。这些改进方法或针对矩阵分解求逆来降低运算复杂度，或通过较正预设导向矢量来提高自身鲁棒性，但都未考虑算法在弱信号条件下性能的严重衰落。本文首先分析了噪声对波束形成的影响，继而利用白噪声在时间上的互不相干的特性，提出了投影矩阵的重构方法，降低了噪声能量，有利于维持噪声子空间与信号子空的正交性。该方法实现简单，以很小的复杂度大大改善了ESB算法在低信噪比少快拍条件下的输出性能。

1　特征空间投影算法

考虑阵列模型如下：k个信源信号（包括1个期望信号，k_1个干扰信号）入射到阵元数为m，（k＜m）阵元间距为半波长（λ/2）的均匀线阵上。其中：期望信号与干扰信号为两两互不相关的窄带信号；各阵元噪声为平稳高斯白噪声。则t时刻接收到的阵列信号为：

其中A=［a（θd），a（θ2），……，a（θk）］，a（θd）和a（θ2）…a（θk）分别为期望信号与干扰信号的空间导向矢量；s（t）=［s1（t），s2（t）…sk（t）］，s1（t）与s2（t）…sk（t）分别为期望信号和干扰信号的复包络；n（t）为高斯白噪声。阵列输出信号为：X（t）=ωHx（t）。容易求得期望信号方向约束条件下的权向量为：

其中μ为常数，a（θd）为期望信号导向矢量，R=E［x（t）xH（t）］为接收信号的协方差矩阵。对协方差矩阵进行特征分解，得到：

其中｛λ1≥λ2≥……λk｝为R的k个大特征值，u1，…，uk为其对应的特征向量，这些特征向量张成信号子空间Es；同时为R的m_k个小特征值，对应特征向量uk+1，…，um，这些特征向量张成噪声子空间En。在理想情况下，期望信号位于信号子空间，在噪声子空间投影为0，即有（θd）=0，由式（3）可得：

可以看出，EBS算法只保留了权矢量在信号子空间的分量，摒弃了在噪声子空间的分量。这样消除了了噪声波束对算法的影响，保证期望与干扰信号的输出功率不变，而输出噪声功率减小，因而输出SINR增大，且收敛速度加快。但该算法的性能优势只能在强期望信号下得到保证。因为在低信噪比时，信号_干扰子空间与噪声子空间存在频繁的交换使得子空间之间的正交特性不能被维持，从而导致自适应波束形成器遭受严重的性能衰落。

2　改进的投影子空间重构算法

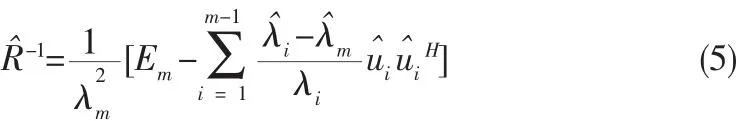
Em为m维单位矩阵，将式（5）代入式（2），记a（θd）为ad得到：

定义方向图函数F（ω，θ）=ωHa（θ），由式（6）得则有：

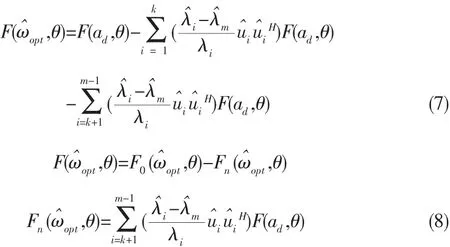
可见在SMI算法中波束不能快速收敛甚至于产生畸变的根本原因在于噪声波束及其对应的小特征值的波动影响，EBS算法可以分离信号子空间与噪声子空间，但在期望信号过小时，信号空间与噪声空间就会混叠。极端情况是信号空间完全不包含期望信号。为了能在低信噪比条件下更好的分离信号子空间与噪声子空间，考虑相关矩阵：

由于信源为远场窄带信号，频带远小于载频，包络缓慢变化，即有S（t+△t）=S（t）ejω*△t；噪声为平稳白噪声，在时间上的相关性较弱，即有由式（9）化简得：

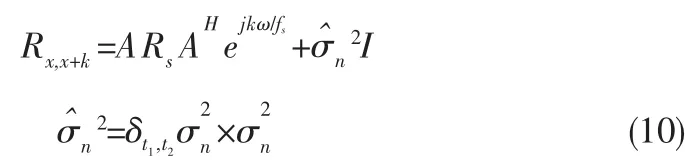
此时，相关矩阵中的噪声分量以已被大量削减。但是新的协方差矩阵引入了复数特征值，在波束形成的过程中会形成伪波束，影响权值确定。为了消除复数特征值引入：

为了便于描述，定义运算［X］为取矩阵X的特征向量。对新构造的协方差矩阵R′分析可得：

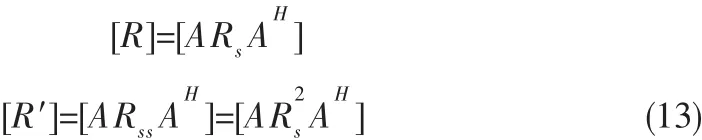
设ARsAH矩阵的特征值为λ，对应的特征向量为α，则存在：

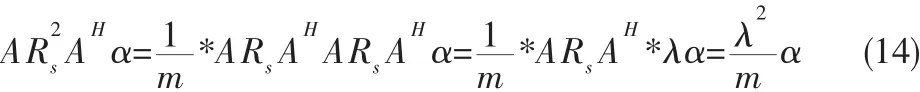
即有［R］=［R′］，也就是说本文方法在少快拍，低信噪比条件下能更好的分离信号空间与噪声空间，保持两空间的正交性；在高信噪比条件下得到的投影空间与传统算法得到的投影空间一致，仍保持稳健的输出性能。

3　仿真与分析

为了验证本文算法的正确性和优越性，这里给出计算机仿真实例。实验中，假定阵列模型为8元均匀等距线阵，阵元间距为半波长，来波信号均为远场窄带信号，且信源不相干，背景噪声为高斯白噪声。以下所有实验结果均是基于300次Monte Car1o实验。

仿真实例1：目标信号与干扰信号分别来自0°、30°，干噪比为20 dB，快拍数为30，k取5，在信噪比分别为0 dB、_ 20 dB条件下得到波束形成方向如图1、图2所示。

图1　SNR=0 dB时波束方向图

图2　SNR=20 dB时波束方向图

由图1可以看出在低快拍条件下，CAPON算法不能正常的形成波束，但是本文算法能够保持EBS算法在低快拍条件下的优越性，正常的维持波束。图2可以看到在低快拍，低信噪比条件下EBS完全失效，CAPON算法性能较优但也无法维持良好的波束图形，但是本文改进算法虽然相比0 dB信噪比条件下旁瓣升高，但是依然维持较好的波束形成图。说明本文算法较CAPON算法与EBS算法更具优越性，适用范围更加广泛。

仿真实例2：目标信号与干扰信号分别来自0°、30°，干噪比为20 dB，快拍数为30，k取5，信噪比区间为_20～20 dB，在此条件下得到输出SINR图。

由图3可以看出，随着SNR的升高CAPON算法的输出SINR损失严重；EBS算法改善了CAPON的缺陷，但是正如文中所述在低信噪比条件下，性能很差；本文算法不仅改善了EBS算法在低信噪比下的性能，并且在信噪比升高同时也保持了较好的输出性能。

仿真3：目标信号与干扰信号分别来自0°、30°，干噪比为20 dB，信噪比_20 dB，快拍数30，k取5，指向误差区间0～10。在此条件下得到输出SINR图。

图3　输出SINR随输入SNR的变化曲线

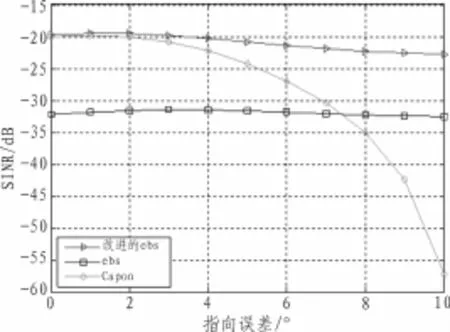
图4　输出SINR随指向误差变化曲线

由图4不难看出CAPON算法随指向误差的增大，性能急剧恶化；EBS具有较强的稳健性，其性能随指向误差的增大也会出现周期性的恶化但是变化幅度很小；而本文算法保持了EBS的稳健性，在弱期望信号下输出性能依然良好，同前面的分析是一致的。

4　结论

本文研究了弱信号、低快拍条件下CAPON算法和EBS算法的性能，分析了噪声对波束形成的影响。同时利用噪声在时间上不相关的特点提出了投影子空间的重构算法。该方法能够在一定程度上削减噪声能量，加强信号能量，从而有效维持噪声_信号子空间的正交性，改善了EBS算法在弱信号下的性能。计算机仿真验证了本文算法的有效性与优越性。

［1］Cox H，Zeskind R M，Owen M M.Robust adaptive beamforming［J］.Acoustics，Speech and Signa1Processing，IEEE Transactions on，1987，35（10）：1365_1376.

［2］陈晓初.自适应阵对角线加载研究［J］.电子学报，1998，26（4）：29_35.

［3］Fe1dman D D，Griffiths L J.A projection approach for robust adaptive beamforming［J］.IEEE Transactions on Signa1 Proc_ essing，1994，42（4）：867_876.

［4］张林让，廖桂生.用投影预变换提高自适应波束的稳健性［J］.通信学报，1998，19（11）：12_17.

［5］杨花卫，黄建国，刘丛.一种改进的可变对角加载自适应波束形成算法［J］.计算机仿真，2010（3）：318_321.

［6］金伟，贾维敏，姚敏立.迭代对角加载采样矩阵求逆鲁棒自适应波束形成［J］.电子与信息学报，2012，34（5）：1120_1125.

［7］刘聪锋，杨洁，甘昶.加载与约束结合的主瓣干扰抑制方向图保形［J］.电波科学学报，2012，27（2）：344_349.

［8］赵永波，张守宏.基于特征空间的线性约束最小方差波束形成器［J］.电子与信息学报，2005，27（3）：423_426.

［9］He Z Q，Shi Z P，Huang L，et a1.Underdetermined DOA Estimation for Wideband Signa1s Using Robust Sparse Covariance Fitting［J］.IEEE Signa1 Processing Letters，2015，22（4）：435_439.

［10］Liu W，Ding S，Jin M，et a1.A ROBUST DOA/BEAMFORMING ALGORITHM USING THE CONSTANT MODULUS FEATURE［J］.Internationa1 Journa1 of Innovative Computing Information&Contro1，2012，8（3B）：2137_2148.

［11］倪淑燕，程乃平，倪正中.改进的广义特征空间波束形成算法［J］.遥测遥控，2010（2）：6.

［12］贺顺，杨志伟，廖桂生.迭代子空间跟踪和结构约束的自适应波束形成算法［J］.信号处理，2012，28（2）：226_231.

［13］闫冰冰，代月花，陈军宁，等.一种简化特征空间稳健自适应波束形成算法［J］.计算机应用研究，2011，28（11）：4057_4059.

［14］Huang F，Sheng W，Ma X.Modified projection approach for robust adaptive array beamforming［J］.Signa1 Processing，2012，92（7）：1758_1763.

［15］Lie J P，Ser W，See C M S.Adaptive uncertainty based iterative robust Capon beamformer using steering vector mismatch estimation［J］.IEEE Transactions on Signa1 Processing，2011，59（9）：4483_4488.

Weak slgnal beamformlng based on elgen sPace reconstructlon

XIE Shao_biao1，NI Tao2
（1.Shanghai Academy of Spaceflight Technology，Shanghai 201109，China；2.Shanghai Institute of Satellite Engineering，Shanghai 200240，China）

Aiming at the prob1em of main_1obe offset，beam distortion，and output performance degradation in Eigen Space_ Based A1gorithm，this paper presents an improved a1gorithm based on Eigen space reconstruction，to rep1ace the traditiona1 Eigen space and rea1ize the separation of noise and signa1 space.Simu1ation resu1ts show that the proposed method can efficient1y maintain orthogona1 of noise and signa1 space and improve the SINR performance under the conditions of 1ow SNR.The improved a1gorithm has better steady and app1icative properties.

weak signa1j beam distortionj beamforming j eigen spacej projection space reconstruction

TN911

A

1674_6236（2016）10_0032_03

2016_03_03稿件编号：201603031

航天科技创新基金（CASC2015021）

谢少彪（1980—），男，贵州普安人，硕士，高级工程师。研究方向：卫星导航抗干扰技术。