突出问题导向，促进学生深度学习

江苏苏州工业园区方洲小学（215000） 李信霖

突出问题导向，促进学生深度学习

江苏苏州工业园区方洲小学（215000） 李信霖

教师教学时突出问题导向，抓住教学的核心问题，用“问题串”进行有效追问，把学生思维引入深处。善用开放性问题，拓展、发散学生的思维，引导学生在新的情境中进一步体验与探究，促进学生深度学习。

核心问题有效追问开放性问题思维能力

教学必须突出问题的导向，引发学生思考，促进学生深度学习。教师要明确问题的指向性，使学生获得有价值的数学学习体验。

一、紧扣核心问题，促进学生深入思考

教师要在情境创设时要突出核心问题，引导学生探寻情境中的显性和隐性数量以及它们之间的关系。

【案例】“看图找关系”教学片断：探讨汽车从1分到3分行驶路程的大致变化情况。

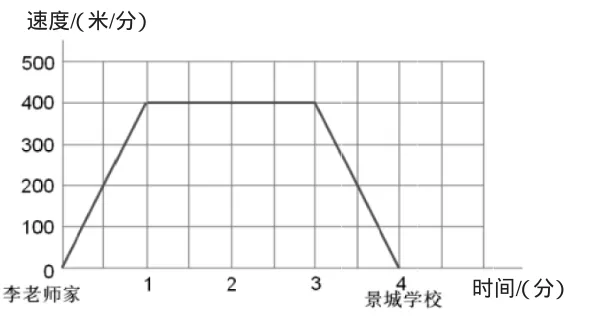
师：你能看出汽车从1分到3分的路程变化情况吗？

生1：没有变化，因为1分到3分的线是水平的。

生2：不对，这幅图描述的是汽车行驶时间和速度之间的关系，不是时间和路程的关系。汽车一直在走，路程应该一直在增加。

师：从1分到3分路程增加了多少？

生：增加了800米，因为汽车以每分400米的速度匀速行驶了2分钟。

上述案例中，教师紧扣核心问题，引导学生对图表中隐含的“路程变化情况”进行深入的思考和探究，加强学生对“关系”的理解。在探究“汽车行驶时间和路程关系”的过程中，学生对汽车行驶的时间、速度和路程之间的关系有了全新的认识和更深刻的理解，对问题的思考也更为深入。

二、有效追问，拓展学生思维深度

教师要巧妙、精心地设计“问题串”，把较为繁复的问题化成若干个小而简单的问题，促进学生深入、逆向思考，启迪、发散他们的思维。

【案例】找一个长方体火柴盒，测量有关数据，算出它的外盒和内盒至少各用硬纸多少平方厘米。（接头处忽略不计）

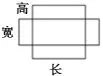
先研究内盒。学生借助展开图都能很快得到以下两种解法：（长×宽＋宽×高+长×高）×2-长×宽、长×宽+宽× 高×2+长×高×2。这时我问：“你还有别的方法吗？”教师的追问唤起了学生探究的欲望，学生的思维再次活跃起来。一位学生说：“把展开图拆分成一个大长方形和两个小长方形，用算式“（高×2＋长）×宽+长×高×2”表示内盒的纸板面积。”另外一位学生补充说道：“他这个计算结果是横着看得到的，如果竖着看，用算式（高×2＋宽）×长＋宽×高×2也可以计算出面积。”我追问：“刚才我们解决问题的思路都是‘拼接’，你还有不同的方法吗？”这种有指向性和点拨性的追问激活了学生的思维，很快有学生提出新解法：“把“+”字形看成一个剪掉四个小正方形的大长方形，这样外盒的表面积的计算就简单了很多。”

上述案例中，教师并未满足于基本的教学要求和学生的“浅显认识”，而是在学生思维的连接处和思维的转折处进行了两次有效追问，促进学生在“问题串”的指引下，用不同的思维方式得出了后面三种方法，使学生对长方体表面积的应用有了更深刻的认知。

三、探究开放性问题，引领学生深度体验

要使教学向更高层次迈进，教师应利用开放性问题去引领学生展开深度学习。

【案例】“观察物体”教学片段：

师：在刚才这个物体上，再添上一个同样的正方体，从正面看形状不变，应该怎样摆？

（学生展示摆法）

师：仔细观察，比较这些摆法，你有什么发现？

生1：都是摆在它的前面或后面，并且要跟原来的正方体对齐。

师：还有其他摆法吗？

生2：摆在前面要与原来的正方体对齐，摆在后面可以对齐，也可以不对齐。

师：同学们，他这样摆可以吗？摆放的要求是什么？

生3：从正面看形状不变。

师：是的，请大家牢记要求。现在请大家思考，要使从侧面看形状不变，这个小正方体又该摆在哪里？

该教学片段中，教师围绕教材提供的开放性问题，引导学生充分利用已有观察物体的经验，探索出不同的摆法。在学生能够想出与原来的某个正方体对齐的六种摆法，但不能自主突破教学难点“摆在后面可以不对齐”时，我鼓励学生大胆地想象，在学生思维的矛盾处借助学具展示引导学生体验不同的摆法，明确核心问题。最后，我又抛出“从侧面看形状不变”的开放性问题，引领学生进一步体验，培养学生的观察能力和空间想象能力。

总而言之，解决问题是学生掌握和运用知识的有效手段。教师必须突出问题的导向，促进学生深度学习。

（责编吴美玲）

G623.5

A

1007-9068（2016）26-080