浅析教材中“平均分”出现歧义的原因

浙江乐清市南华寄宿学校（325600） 却立泉　童小艳　叶嬉嬉

浅析教材中“平均分”出现歧义的原因

浙江乐清市南华寄宿学校（325600） 却立泉童小艳叶嬉嬉

教材是教师教授知识，学生认识新事物和学习新知识的重要载体。课堂教学中，学生对教材呈现的“平均分”提出了异议，追根溯源，并非学生的认知出现了偏差，而是教材的编排引发歧义。

教材 平均分 歧义 面积 体积

“平均分”与平均数不同，是分物时所用的一种思想，指在分物体的时候要尽可能地分完，而且要使每一份得到的数相等。下面，我就从“平均分”的表示方法入手，分析、探讨教材中“平均分”出现歧义的原因。

一、“平均分”的表示方法

1.用面积（或体积）表示的“平均分”（如下图）

这里，图形涂色的部分很直观，很容易理解，符合学生的一般认知规律。

2.用数量表示的“平均分”

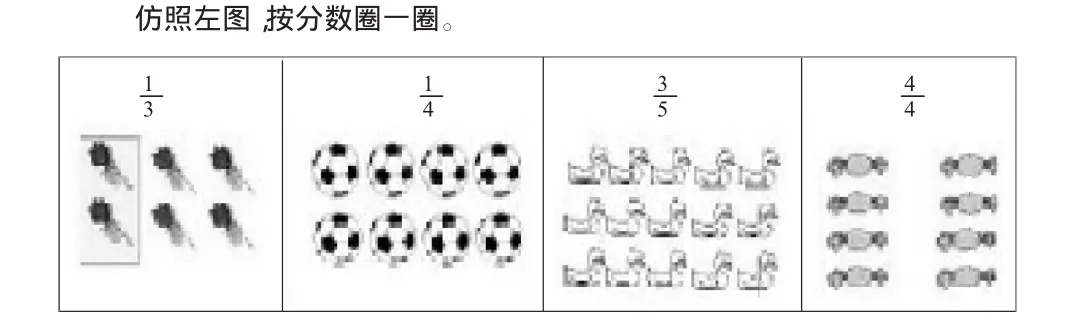
关于单纯的数量上的平均分，在平时的生活中常常遇到，学生也比较容易理解。

3.“面积”或“体积”和数量同时存在的情况

对于这道题的回答，学生出现了不同的观点。有的学生说：“把6个苹果看成一个整体，平均分成了3份，就是平均分！”有的学生则重复着“标准答案”，而大多数学生则跟着点头认可。也有的学生说：“老师，这不是平均分！”学生经过一番讨论，最终提出异议的学生被占优势的“标准答案”所淹没。

二、通过调查分析，“平均分”出现分歧的情况确实存在

为什么会有学生认为这不是平均分呢？依据是什么？我课后进行反思，并设计了两道题（如下图），对上过此课的三个班级随机各抽取一个组（合计34人）进行测试和调查。

例（1） 下面三幅图有什么共同点和不同点？每幅图其中的一份都可以用哪个分数表示？

例（2） 下面两幅图有什么共同点和不同点？每幅图其中的一份都可以用哪个分数表示？

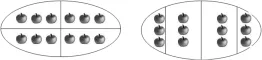
调查结果显示：例（1），共同点是都把相应的苹果平均分成了四份，其中的一份都可以用四分之一来表示；不同点是每幅图的苹果总数不同，所以每份的苹果个数也就不同。对于例（1），学生回答的正确率为100％。例（2），学生的回答出现了分歧，有10名学生虽然迅速地说出第一幅图平均分成了四份，其中的一份可以用四分之一表示，但是他们对第二幅图的第一反应却说不是平均分成了四份，弃用四分之一而选用十二分之三来表示其中的一份。这是由于学生无法领会集合圈这一数学符号的意思，故不用四分之一而选用十二分之三来表示。这不得不引起我们教师的深思：在平时的授课中，我们应该用什么样的方式，把知识更好地传授给学生，让他们能更好地理解所学的知识？

三、“平均分”出现分歧的原因总结

针对教材“面积”或“体积”和数量同时存在的这种编排设计，我翻阅了多种同类知识的教材版本，发现苏教版和北师大版教材均未出现人教版教材中这种“积（面积、体积）”“物（数量）”重叠的编排设计。这样编排的设计意图是让学生体会单位“1”，培养学生的符号意识，但是却不符合学生的认识规律，容易造成学生认知混乱。若非要“积”“物”重叠的设计，可以把集合圈换成矩形或圆形，这样无论是从“积（面积、体积）”，还是从“物（数量）”方面进行观察，都能做到等量齐观，会更符合学生的认知规律。

张奠宙教授曾对小学数学教材提出五点建议：一是必须坚决杜绝错误；二是保持数学的准确性特点；三是把教学的重点放在解释数学的本质上；四是数学的科学性需要用数学思想方法加以体现；五是要做到与时俱进，不断变化。同时，我也斗胆提一点建议，那就是教师应尊重学情，遵从学生的认知规律，循序渐进地进行教学。

（责编蓝天）

G623.5

A

1007-9068（2016）26-024