精心设计，让学习真发生——以“表面积的变化”教学为例

江苏溧水区经济开发区沙河小学（211200） 龚有琦

精心设计，让学习真发生
——以“表面积的变化”教学为例

江苏溧水区经济开发区沙河小学（211200） 龚有琦

“表面积的变化”教学难度较大，属于知识的进一步应用。通过引导学生经历拼摆图形、合作交流、自主探究、合情推理、归纳演绎等一系列过程，让学生学习真正发生的同时，增强学生的应用意识和创新意识。

表面积的变化拼摆合作推理

《义务教育数学课程标准》在“实施意见”中指出：“教师在教学过程中，应该设计适当的教学活动，引导学生通过观察、尝试、估算、归纳、类比、画图等活动发现一些规律。”

课堂教学中，教师绝不能过于“勤快”，将知识“咀嚼”过细、过碎“喂给”学生，也不能面面俱到，“准确到位”，越俎代庖，学生无需动脑思考，不需动手探究，便轻易可得“知识”。长此以往，学生将不会思考，不愿思考。教学中需给学生一点空间、一处“留白”、一些自主，让学生自己去观察思考、操作探究、归纳概括、发现规律，在活动中探究知识，获取经验。

对于“探索规律”中“表面积的变化”的教学，教师要精心设计，学做“懒”教师，培养勤学生，有意“留白”，给予足够时空，促进学生动手操作，拼摆图形，让学生在活动中寻找规律、发现规律、归纳规律和运用规律，使学习真发生。

【背景】

在学生学习了“图形与几何”中“长方体和正方体”这一单元后，教材在“综合与实践”课程内容中安排了“探索规律”“表面涂色的正方体”内容，为有利于探索“当用n表示把大正方体的棱平均分的份数，2面涂色和1面涂色的小正方体个数分别用a、b表示，写出n和a、b的关系”这一规律，教师先进行“表面积的变化”规律探索的教学，其内容是探索几个相同的正方体相拼，拼得的立体图形与原来几个正方体表面积之和的关系，发现其变化规律并加以运用。

本课设计了2个层次：第一层“拼拼算算，探索规律”和第二层“拼拼说说，运用规律”；有4个活动，即4个片断：（1）用2个相同的正方体拼出1个长方体，感知2个正方体拼成1个长方体后，其表面积减少了原来正方体2个面的面积。（2）用3个、4个甚至更多个相同的正方体摆成一行拼成长方体，求其表面积分别减少了多少，并探索表面积的变化规律。（3）用2个相同的长方体拼成1个大长方体，求其表面积的变化情况。（4）用8个相同的正方体怎样拼成表面积最小的1个长方体。

要求学生通过动手拼摆图形、直观观察、合情推理、综合归纳后发现规律。

【片段1】

师：在桌上有一些小正方体，你能将2个体积都是1立方厘米的小正方体拼成1个长方体吗？

生：能！太简单了！

师：好，请大家动手拼一拼。

（学生动手拼图，很快拼成）

师：有的同学拼成横着的1个长方体，有的同学拼成竖着的1个长方体.....想一想，它们的体积有没有变化？

生：没有。

师：那表面积呢？

生：变小了。

师：变小后有什么规律吗？

（教师揭示（书写）课题：表面积的变化）

师：大家再仔细观察刚才拼成的长方体，它的表面积比原来2个小正方体表面积的和小了多少？

生1：2个同样的正方体拼成1个长方体后，表面积减少2个正方形面的面积。

生2：拼成长方体的表面积比原来两个正方体表面积的和减少了2平方厘米。

（教师板书：拼1次减少2个面）

感悟：拼摆图形，为发现规律奠定基础

“综合与实践”课程，“教师要放手让学生参与”，“重在实践”，让学生真的“动”起来，应遵循小学生的认知规律，加强操作活动，在操作活动中发现规律、探究规律、归纳规律和运用规律。上述环节就是学生通过动手拼摆图形、观察思考，发现拼摆图形前后表面积的变化，得知2个同样的正方体拼成1个长方体后，表面积减少了原来正方体2个面的面积，为发现其规律奠定最基础的知识。

【片段2】

师：如果用3个、4个或更多个同样的正方体摆成一排，表面积会怎样变化呢？4人小组合作，先拼一拼，再仔细观察，并把下面表格填完整。从中你能发现什么规律吗？

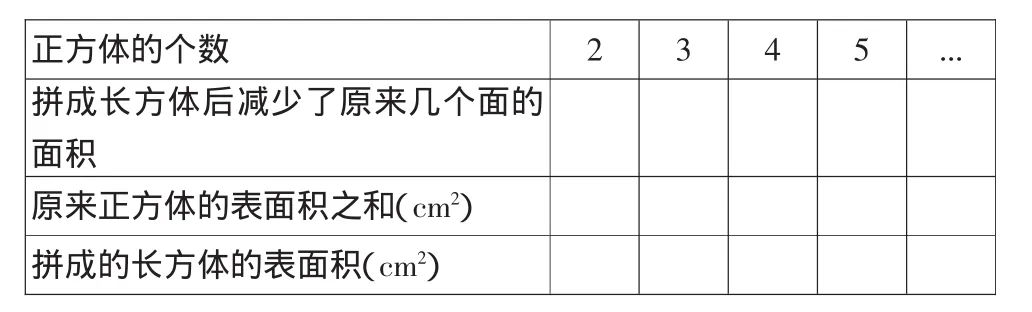
正方体的个数　2　3　4　5　...拼成长方体后减少了原来几个面的面积原来正方体的表面积之和（cm2）拼成的长方体的表面积（cm2）

（学生把2个、3个、4个、5个……同样的正方体摆成一排，很快发现它们依次减少了2个面、4个面、6个面、8个面……）

师：若是10个正方体又该怎么填？n个呢？

（学生思考，探究出一般规律：（n-1）×2）

感悟：合作交流，探索发现一般规律

学生参与学习过程，是个体与群体相融合的过程。在课堂教学中组织学生合作交流，营造积极思考、勇于探索、畅所欲言的学习氛围，可以促进学生积极主动地进行探究学习。通过4人小组合作交流，学生把几个同样的正方体拼成1个较大的长方体，在边操作、边思考、边交流中，相互启发，达成共识，认同拼摆图形前后表面积变化存在着一定的规律，并及时将关注点引导到寻找规律上，结合表格中的数据寻找这种规律，当拼摆正方体的个数趋于众多（n）时，拼成长方体后减少的面就不可能用具体的数来表示，必须要进行合情推理，从而得出一般规律，即n个正方体摆成一行拼成一个长方体，其减少面的个数为（n-1）×2。

【片段3】

师：刚才我们研究了3个、4个甚至更多个相同的正方体摆成一行拼成长方体时，表面积的变化规律，如果把相同的长方体拼在一起，会有规律吗？又会有什么样的规律呢？大家想研究吗？

生：想！

师：真棒！

师（拿着2个长方体纸盒，指着纸盒）：这是2个同样的长方体纸盒，长是5厘米，宽是4厘米，高是3厘米，你能用这2个长方体纸盒拼成3个大小不同的大长方体吗？4人一小组，小组合作，拼拼看。

（学生将课前准备好的学具摆上课桌，认真动手一一拼起来。教师对学生的操作予以充分肯定后，将重点放在引导学生寻找规律上。）

师：大家用2个同样的长方体拼成了3个大小不同的大长方体，联系你们刚才拼摆的过程，有什么发现吗？

（学生回顾，沉思，重新摆弄，小声议论……）

师：有发现了？

生1：拼摆成长方体后，体积没有变化，表面积有变化。

师：很好，和用正方体拼摆图形时一样，体积没有变化，表面积变化了。

师：谁能说说表面积是怎样变化的？

生2：和用正方体拼摆图形一样，都比原来减少了2个面的面积，不同拼法减少的面积大小不同。

师：对，谁来指一指，少的2个面在哪？其他同学看着拼摆的图形并在脑中想象，少了哪2个面？

师：在已拼成的长方体中，哪个大长方体的表面积最大，哪个最小？你是怎样想的？

（引导学生发现：3号长方体表面积最大，1号长方体表面积最小；当减少的面积越少时，拼成的大长方体的表面积就越大。）

师：请算一算，3个大长方体的表面积分别比原来减少了多少？

【片段4】

师：大家通过3次动手拼摆图形知道，几个相同正方体或长方体拼成一个较大的长方体时，表面积都发生了变化，而且都有一定的变化规律。现在，老师要把8个棱长都是1厘米的正方体礼品盒包装在一起，怎样包装最节省包装纸？

师：最节省包装纸是什么意思？

生1：就是用的包装纸最少。

生2：就是把8个礼品盒拼在一起时，表面积最小。

师：理解得非常准确。现在4人小组合作，先动手拼一拼、摆一摆，再计算。

（经过小组合作拼摆图形、观察思考、推理计算，学生从交流反馈中发现3种不同拼法，得出3种不同的表面积：34 cm2、28 cm2和24 cm2。）

师：表面积是24 cm2的是怎样包装的？

生3：拼成的是1个大正方体。

师：拼成大正方体时，表面积最小，也就是最节省包装纸。通过多次不同的拼摆图形可知：把同样的小正方体或长方体拼成大长方体时，重合的面越多，表面积减少就越多，反之，重合的面越少，表面积减少的也越少。

感悟：自主探索，注重实践和综合应用

数学课程标准在谈“课程内容”时指出：“‘综合与实践’内容设置的目的在于培养学生综合运用有关的知识与方法解决实际问题，培养学生的问题意识、应用意识和创新意识，积累学生的生活经验，提高学生解决现实问题的能力。”片段3中，是让学生用2个相同的长方体拼成1个大的长方体，再观察它的表面积变化情况；片段4中，是把8个体积为1立方厘米的正方体礼品盒包装在一起，求最节省包装纸的拼图。上述2个教学片断，学生都经历了小组合作、交流讨论、自主探究，学生在掌握拼摆图形表面积变化规律后，也都能运用这一知识与方法解决不同的实际问题。

【后记】

“表面积的变化”的教学内容属于知识的进一步应用，难度较大。课例中，教师对教学内容精心设计，并引导和启发学生切实经历拼摆图形、合作交流、自主探究、合情推理、归纳演绎等一系列过程。显然，在学习真正发生的同时，学生的应用意识和创新意识都得到了增强。

（责编金铃）

G623.5

A

1007-9068（2016）26-012