非线性幸福模型的自适应追踪广义投影同步

王晓东，史丽敏，毛北行

（郑州航空工业管理学院 理学院，郑州 450015）

非线性幸福模型的自适应追踪广义投影同步

王晓东，史丽敏，毛北行

（郑州航空工业管理学院 理学院，郑州 450015）

研究了一类三阶非线性幸福模型的自适应追踪广义投影同步问题，并基于Lyapunov稳定性理论和分数阶微积分理论得到了整数阶和分数阶幸福模型实现广义投影同步的充分条件。数值仿真结果表明了该方法的可行性。

幸福的动力学模型；分数阶模型；同步

人们在研究混沌同步方面已取得一些有价值的成果［1-7］，但对用数学模型描述幸福问题却关注得比较少。J.C.Sprott［8］通过求特征根的方法从动力学角度研究了幸福模型，孙玉霞等［9］从动力学的角度对受驱动的非线性幸福模型进行了解析，但他们的研究都不涉及混沌同步问题。在本文中，我们研究了一类三阶幸福模型的自适应追踪广义投影同步问题，基于Lyapunov稳定性理论和分数阶微积分的相关理论得到了幸福模型实现广义投影同步和误差趋近于参考信号的充分条件，并通过例子说明了该方法的可行性。

1　主要结果

在本文中，我们将考虑含有噪声扰动和未知参数的整数阶幸福模型

其中，F是未知的，n（t）为高斯白噪声且满足|n( t)| ≤k。同时，我们还将通过设计控制器和适应律使模型（1）追踪广义投影同步于参考信号,即

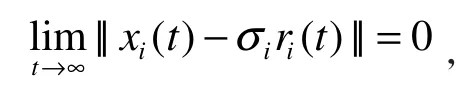
其中σi为常数。

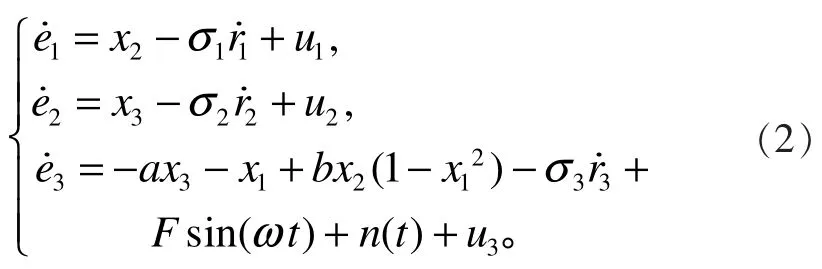
根据Lyapunov稳定性理论，很容易得到模型误差是渐近稳定的，并且模型（1）广义投影同步于给定的参考信号

定义1［10］：Caputo分数阶导数定义为

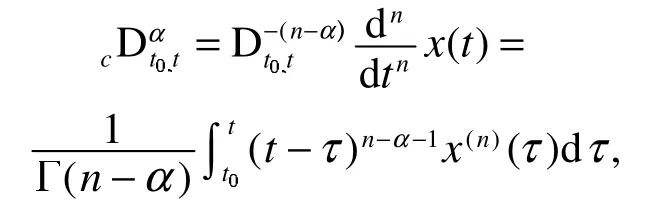
现在，我们虑含有噪声扰动和未知参数的分数阶幸福模型

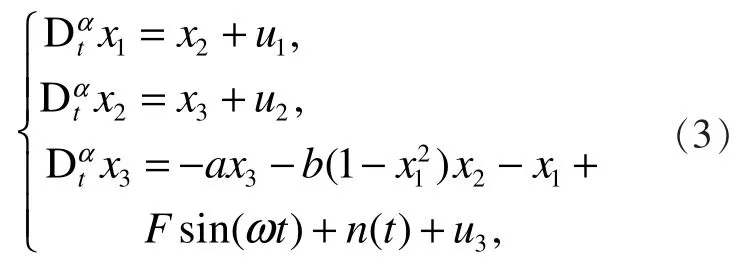
其中，F是未知的，n（t）为高斯白噪声。

下面通过设计控制器和适应律使模型（3）广义投影同步于参考信号，即

其中σi为常数。

2　仿真算例

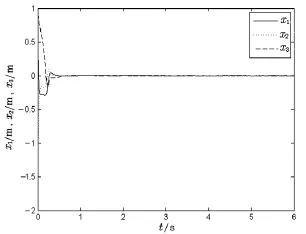
图1　模型追踪到平衡点的曲线

情形2：若r1、r2和r3为分数阶混沌模型的变量，则有

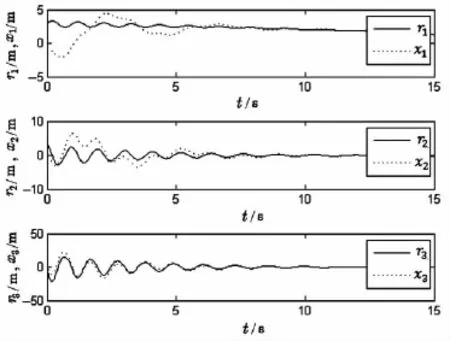
图2　模型的追踪曲线

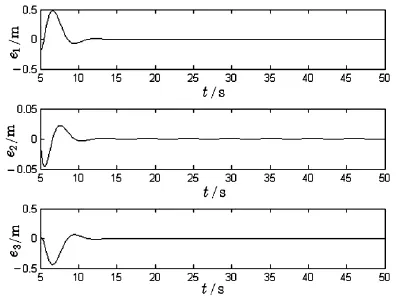
图3　模型的误差曲线

3　结束语

在本文中，我们基于Lyapunov稳定性理论和分数阶微积分的相关理论，研究了一类具有外加激励的整数阶和分数阶幸福模型的自适应追踪广义投影同步问题，得到了整数阶和分数阶模型实现广义投影同步的充分条件，并通过例子说明了该方法的可行性。

［1］AHMADWM，El-KHAZALIR.Fractional-orderDynamical Models of Love［J］.Chaos，Solitons&Fractals，2007，33 （4）：1367-1375.

［2］WANG X，HE Y.Projective Synchronization of Fractional Order Chaotic System Based on Linear Separation［J］. Physics Letters A，2008，372（4）：435-441.

［3］张燕兰.分数阶Rayleigh-Duffing-like系统的自适应追踪广义投影同步［J］.动力学与控制学报，2014（4）：348-352.

［4］邵书仪，陈谋.一类分数阶非线性混沌系统的同步控制［J］.计算机仿真，2015（4）：394-398.

［5］SPROTT J C.Dynamical Models of Love［J］.Nonilear Dynamics，Phychology and Life Science，2004，8（3）：303-313.

［6］ORSUCCI F.Happiness and Deep Ecology：On Noise，Harmony，and Beauty in the Mind［J］.Nonlinear Dynamics，Psychology，and Life Sciences，2001，5（1）：65-76.

［7］LARSON J，MCGRAW A P，CACIOPPO J.Can People Feel Happy and Sat at the Same Time［J］.Journal of Personality and Social Psychology，2001，8（1）：684-696.

［8］SPROTT J C.Dynamical Models of Happiness［J］.Nonlinear Dynamics，Psychology，and Life Sciences，2005，9（1）：23-36.

［9］孙玉霞，乔晓华，包伯成.受驱动非线性幸福模型的动力学解析［J］.电路与系统学报，2012（1）：92-95.

［10］郝建红，宾虹，姜苏娜，等.分数阶线性系统稳定理论在混沌同步中的简便应用［J］.河北师范大学学报（自然科学版），2014（5）：469-475.

【责任编辑王云鹏】

Adaptive Tracking Generalized Projection Synchronization of Nonlinear Happiness Models

WANG Xiaodong，SHI Limin，MAO Beixing
（College of Science，Zhengzhou Institute of Aeronautical Industry Management，Zhengzhou 450015，China）

The problem of adaptive tracking generalized projection synchronization of three-order nonlinear happiness models was studied in this paper.The sufficient conditions of integral order and fractional order happiness models realizing generalized projection synchronization which was based on Lyapunov stability theory and fractional order calculus theory were obtained.Numerical simulations results of chaotic system verified the effectiveness of the proposed method.

happiness dynamical model；fractional order model；synchronization

O231.1

A

2095-7726（2016）09-0011-03

2016-04-02

国家自然科学基金青年基金项目（NSFC11501525）；河南省科技厅软科学研究项目（142400411268）；河南省教育厅高等学校重点科研项目（15B110011）

王晓东（1973-），男，河南通许人，讲师，研究方向：复杂网络与混沌同步。