多个障碍物散射问题解的存在性与唯一性

吴庆华

（湖北工程学院 数学与统计学院，湖北 孝感432000）

多个障碍物散射问题解的存在性与唯一性

吴庆华

（湖北工程学院 数学与统计学院，湖北 孝感432000）

考虑了具有不同边界条件的多个障碍物的混合散射问题，分别利用Rellich引理、Fredholm定理证明了该问题解的存在性和唯一性。

多个障碍物；散射问题；存在性；唯一性

人们经常用Helmholtz方程边值问题描述时间调和的声波散射问题。人们早期研究散射问题时考虑的都是单个障碍物。R.Kress［1］和分别考虑了带Dirichlet和Neumann边界条件的一个障碍物的散射问题，并通过边界积分方程证明了解的存在性和唯一性。R.Kress等［3］借助边界积分方程研究了满足第三类边界条件的散射问题。目前，人们更关注复杂散射问题，该问题可以分成两类：一类是多层的复杂散射问题［4-5］，另一类是多个障碍物的复杂散射问题［6-7］。P.A.Martin［8］研究了点态的多个障碍物的复杂散射问题。F.B.Hassen1等［9］借助分裂法研究了多个障碍物散射问题的散射体重构问题。CHENG Jin等［10］借助探针法研究了多个散射体的复杂散射问题。M. Ganesh等［11］研究了三维空间中的多个散射体的复杂散射问题。散射问题包括正散射问题和逆散射问题，正散射问题是逆散射问题的研究基础，研究逆散射问题就是利用正散射问题的解重构散射体的位置和形状。在本文中，笔者考虑了多个障碍物的复杂正散射问题，并利用调和声波满足的Helmholtz方程、声波在障碍物上满足的边界条件、Rellich引理和Fredholm定理证明了该散射问题解的唯一性和存在性。

1　两个障碍物的混合散射问题

为了简单起见，笔者考虑了两个障碍物的情形，设D1和D2是两个互不相交的障碍物，其中一个表面是声硬的，另一个表面有涂层。调和声波入射的整体场U= ui+ us满足Helmholtz方程边值问题

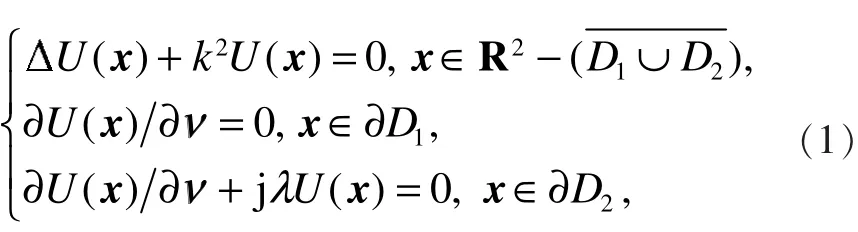
其中，j是虚数单位，x和d分别是观察点和入射点的位置，λ是大于0的常数，ν表示沿各边界∂D1或∂D2指向区域外部的单位法向量。是已知的入射波，us是未知的散射波，此外，散射波us还应满足Sommerfeld散射条件

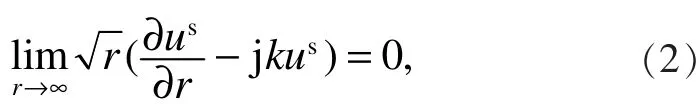
下面证明满足散射条件（2）的问题（1）的解的唯一性和存在性。

2　解的唯一性

因为入射波ui满足Helmholtz方程，所以在考虑未知散射波us时，问题（1）则改写为

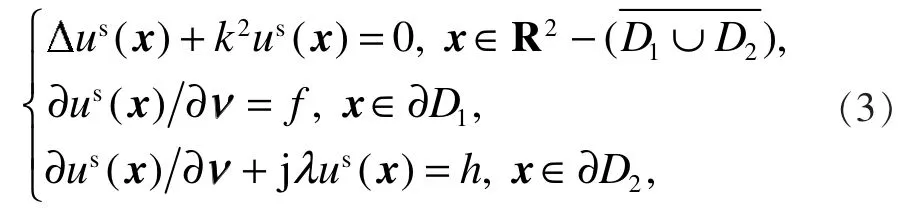
定理1：当λ>0时，满足Sommerfeld散射条件（2）的问题（3）最多只有一个解。

证明：散射问题（3）有唯一解的充要条件是该问题在边界条件f=h=0时只有零解。下面证明问题（3）的齐次边值问题只有零解。

设BR是圆心在原点，半径R充分大的圆，且,∂BR为BR的边界，则由Green公式可得

因为k>0,所以只要取λ≥0,就有

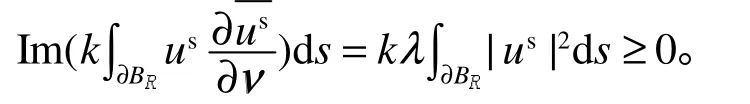
由Rellich引理［12］可以得出在R2−BR内有us= 0。根据解的唯一连续性定理［12］可以得出us=0在内恒成立，故定理1的结论成立。

3　解的存在性

下面利用边界积分方程和Fredholm定理证明满足条件（2）的散射问题（3）存在解。

其中x ∈∂D1；

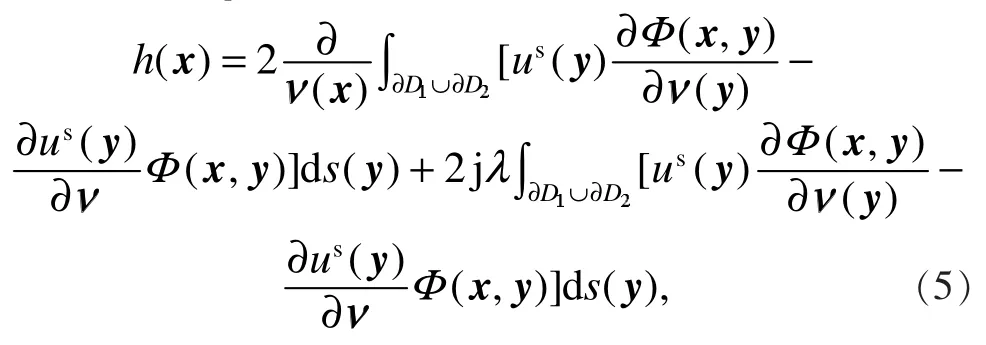
其中x ∈∂D2。

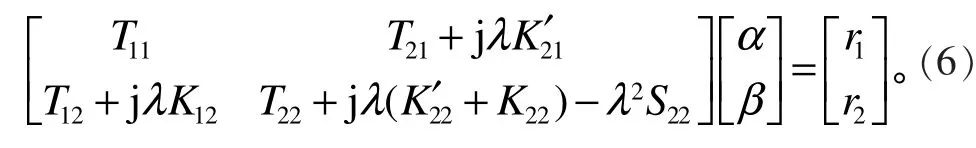
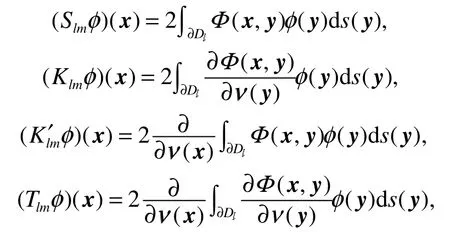
其中x∈∂Dk,l和m分别取1或2。

从以上分析过程可以看出，满足散射条件（2）的问题（3）有解的充要条件是边界积分方程组（6）有解。

定理2：当k2不是?算子在D1内的Neumann特征值时，边界积分方程组（6）存在唯一解。

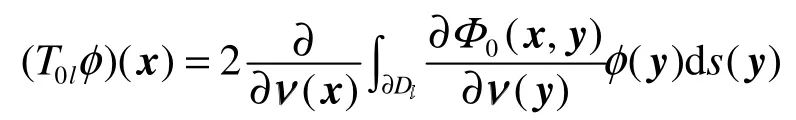
下面证明方程组（6）左端的边界积分算子是单射时，方程组（6）有唯一解。

设(φ1, φ2)是齐次方程组的解，令

和

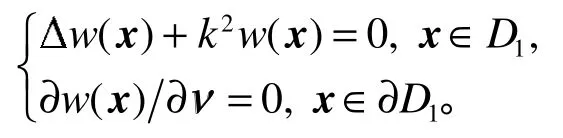
同时，w(x)还满足

和

根据上述四个问题解的唯一性，k2只要不是算子在D1内的Neumann特征值，在D1和D2的内部和外部就有w=0。又由位势函数的跳跃关系可知，φ1=,因而齐次方程组（7）只有零解。

由以上证明过程和Fredholm定理可知，边界积分方程组（6）存在唯一解。

在以上证明过程中，用到的(⋅)+和(⋅)−分别表示x从区域外部和内部趋于相应边界时的极限。

定理3：当k2不是算子在D1内的Neumann特征值时，满足散射条件（2）的问题（3）存在唯一解,且有

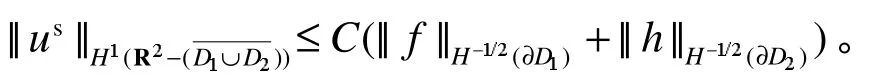
证明：由定理1和定理2知，散射问题（3）存在唯一解，将方程组（6）的解代入由Green表示的形式解就可以得到该定理的结论。

4　结束语

在本文中，笔者仅考虑了两个障碍物的复杂正散射问题，并分别利用Rellich引理、Fredholm定理证明了该问题解的存在性和唯一性。多个障碍物的正散射问题和逆散射问题还有待做进一步讨论。

［1］KRESS R.On the Numerical Solutions of a Hypersingular Integral Equation in Scattering Theory［J］.Journal of Computational and Applied Mathematics，1995，61（3）：345-360.

［2］MONCH L.On the Numerical Solution of the Direct Scattering Problem for an Open Sound-hard Arc［J］. Journal of Computational and Applied Mathematics，1996，71（2）：343-356.

［3］KRESS R，LEE K M.Integral Equation Methods for Scattering from an Impedance Crack［J］.Journal of Computational and Applied Mathematics，2003，161（1）：161-177.

［4］LIU X D，ZHANG B.A Uniqueness Result for the Inverse Electromagnetic Scattering Problem in a Two-layered Medium［J］.Inverse Problems，2010，26（10）：105007.

［5］ZHANG H W，ZHANG B.A Newton Method for a Simultaneous Reconstruction for an Interface and Buried Obstacle from Far-field Data［J］.Inverse Problems，2013，29（4）：045009.

［6］ BALABANE M.Boundary Decomposition for Helmholtz and Maxwell Equations 1：Disjiont Sub-scatterers［J］. Asymptotic Analysis，2004，38：1-10.

［7］CASSIER M，HAZARD C.Multiple Scattering of Acoustic Waves by Small Sound-soft Obstacles in Two Dimensions：Mathematical Justification of the Foldy-Lax Model［J］. Wave Motion，2013，50（1）：18-28.

［8］MARTINPA.MultipleScattering：Encyclopediaof MathematicsandItsApplications［M］.Cambridge：Cambridge University Press，2006：1-70.

［9］HASSEN F B，LIU J J，POTTHAST R.On Source Analysis by Wave Splitting with Applications in Inverse Scattering of Multiple Obstacles［J］.Journal of Computational Mathematics，2007，25（3）：266-281.

［10］CHENG J，LIU J J，NAKAMURA G，et al.Recovery of Multiple Obstacles by Probe Method［J］.Quarterly of Applied Mathematics，2009，67（2）：221-247.

［11］GANESH M，HAWKINS S C.Simulation of Acoustic Scattering by Multiple Obstacles in Three Dimensions［J］. ANZIAM Journal，2008，50：C31-C45.

［12］COLTON D L，KRESS R.Integral Equation Methods in Scattering Theory［M］.New York：Springer-Verlag，1983：16-36.

［13］CAKONI F，COLTON D.The Linear Sampling Method for Cracks［J］.Inverse Problems，2003，19（2）：279-295.

【责任编辑王云鹏】

The Existence and Uniqueness of Solutions to Multiple Obstacles Scattering Problems

WU Qinghua
（School of Mathematics and Statistics，Hubei Engineering University，Xiaogan 432000，China）

The multiple obstacles scattering problems with different boundary conditions were considered in this paper.The existence and uniqueness of the solutions were respectively proved by using Fredholm's theorem and Rellich's lemma.

multiple obstacles；scattering problems；existence；uniqueness

O175.24；O175.25

A

2095-7726（2016）09-0001-03

2016-04-19

吴庆华（1977-），女，湖北天门人，副教授，博士，研究方向：偏微分方程。