基于ANSYS Workbench的低噪声海水泵有限元分析

李永东，张海鹰，马小录，白坤雪，高爱军

（中国船舶重工集团公司 第705研究所，陕西 西安，710077）

基于ANSYS Workbench的低噪声海水泵有限元分析

李永东，张海鹰，马小录，白坤雪，高爱军

（中国船舶重工集团公司 第705研究所，陕西 西安，710077）

为进一步优化设计鱼雷用低噪声海水泵，利用工程仿真技术集成平台ANSYS Workbench对鱼雷用低噪声海水泵关键零部件进行了静力学及动力学有限元分析，得到了某种工况下低噪声海水泵关键零部件的受力情况及振动特性，并通过对齿圈进行谐响应分析，预测结构的持续动力学特性。该分析结果可为低噪声海水泵的设计及试验提供理论支持，对于缩短研发周期、节省试制费用和提高设计质量有一定的参考作用。

鱼雷；低噪声海水泵；振动特性；谐响应；有限元分析

0　引言

海水泵作为热动力鱼雷中重要的海水增压元件，目前主要采用渐开线外啮合齿轮泵或叶片泵［1］。由于泵结构自身的工作特点所产生的压力脉动会沿着海水的流动通路传递，引起相关零部件和管道振动，并通过鱼雷壳体向外辐射噪声［2］。为减小外啮合齿轮海水泵出口压力脉动，通常会采取增加齿轮齿数、侧板设置卸荷槽、提高齿轮加工精度［3］及在泵出口设置减振管［2］等方法。

鱼雷用低噪声海水泵则通过采用内啮合渐开线齿轮泵的结构形式减小海水泵的出口压力脉动。低噪声海水泵具有流量脉动小、无困油、噪声低等优点［3］。在排量及外形尺寸相同的情况下，其出口流量脉动系数远低于外啮合齿轮泵。

目前，针对内啮合齿轮泵的研究主要集中在某个零件及单个结构的分析计算方面［4］，很少采用有限元方法对泵进行静力学及动力学分析。ANSYS Workbench作为新一代多物理场协同CAE（computer aided engineering）仿真环境不但继承了ANSYS经典平台（ANSYS Classic）在有限元仿真分析上的所有功能，而且融入了UG、PRO/E 等CAD软件强大的集合建模功能［5］。文中利用有限元仿真平台ANSYS Workbench对低噪声海水泵结构进行仿真，通过对相关结构进行静力学及动力学分析，为工程设计及试验提供理论支撑。

1　低噪声海水泵工作原理

低噪声海水泵主体结构由一对内啮合的渐开线齿轮组成［6］，并采用轴向及径向间隙自动补偿的密封装置，从而提高了泵的容积效率，其输出功率及输出压力随之得到大幅度提高。

低噪声海水泵结构原理如图1所示，主动齿轮轴和齿圈之间安装一对活动的月牙板，以便把吸油腔和压油腔隔开。当齿轮轴按箭头所示方向旋转时，齿圈也以相同方向旋转，左半部轮齿脱开啮合的地方齿间容积逐渐扩大，形成真空，液体在外部压力作用下进入低压腔并填满各齿间。而右半部轮齿进入啮合处齿间容积逐渐缩小，形成高压腔，工作介质被挤压出去［7］。轮齿不停地转动，齿轮泵就不停地吸水和压水。

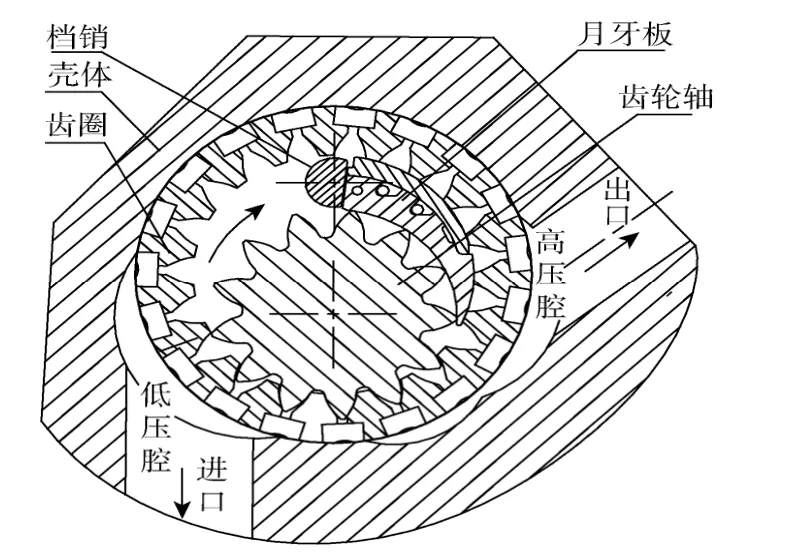
图1　低噪声海水泵结构原理图Fig.1　Principle of low noise seawater pump

海水泵工作过程中，齿轮副的啮合运动及进口压力的大范围变化导致齿轮轴及齿圈承受较大的单向不平衡力，而且由于输入转矩的激励将可能引起海水泵零部件的振动。为了满足海水泵复杂的工作条件及减小振动对泵性能的影响，需要对海水泵各零部件进行力学分析。

2　有限元分析前处理

在有限元仿真平台 ANASYS Workbench中分别调用静力学（static structural）、模态分析（modal）、谐响应（harmonic response）分析模块进行仿真计算。由于ANSYS Workbench在各分析模块中可以自动创建数据连接以共享几何模型［8］，因此对于需要同时进行静力学分析和动力学分析的零件只需在静力学分析时导入UG模型并进行相关有限元分析前处理工作，动力学分析时只要共享静力学分析部分前处理数据即可完成大部分动力学分析的前处理工作。

低噪声海水泵零部件的有限元分析前处理流程如图2所示。

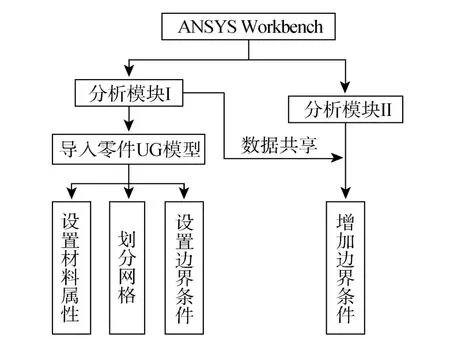
图2　ANSYS Workbench前处理分析流程Fig.2　Pre-process analysis flow chart of ANSYS Workbench

3　仿真计算与分析

3.1理论模型和仿真流程

有限元方法是用于求解各类工程问题的一种数值计算方法。对于1个实际弹性结构的连续系统，用有限元方法将其离散化后，可获得n个自由度离散系统的动力平衡方程［8］，系统的有限元计算方程为

其中: M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；u..为加速度向量；u.为速度向量；u为位移向量；F为外载荷矩阵。

静力学分析为受到静态载荷的作用下，分析结构应力分布与应变。 分析过程中与时间t有关的量均被忽略，则式（1）简化为

低噪声海水泵相关零部件模型属于无阻尼多自由度线性振动系统，其运动学方程

无阻尼模态分析模型为典型的特征值问题，其解形式为

将式（4）代入式（3）得

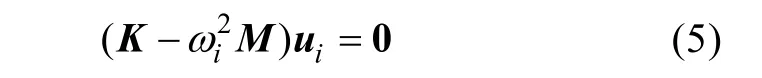
式中: ωi为系统振动圆频率；ωi对应的特征向量ui为自振频率对应的振型，特征根为ωi2。

谐响应分析用于确定线性结构在简谐周期载荷下的稳态响应［9］。谐响应分析的载荷是随时间正弦变化的简谐载荷［10］，则系统动力学方程为

式中，ωT为周期载荷圆频率。

仿真流程如图3所示。

图3　仿真流程Fig.3　Flow chart of simulation

3.2静力学分析

齿轮的啮合过程是复杂的非线性问题［11］，文中利用ANSYS Workbench静力学分析模块对齿轮啮合过程中某一瞬时的齿轮接触应力及齿轮轴、齿圈的静力学特性进行仿真计算，以预测低噪声海水泵在齿轮啮合时工作部件的应力分布状态。齿轮啮合处接触应力云图如图4所示，最大接触应力为360.57 MPa。齿轮轴应力云图见图5，最大等效应力为142.03 MPa。齿圈应力云图见图6，最大等效应力为106.57 MPa。

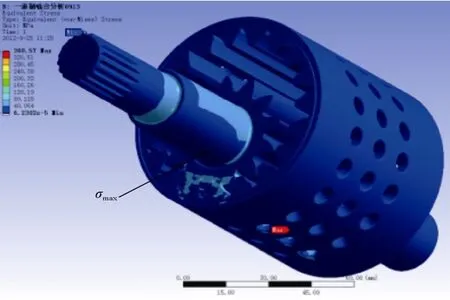
图4　齿轮啮合接触应力分布云图Fig.4　Contours of contact stress distribution of gears

图5　齿轮轴应力分布云图Fig.5　Contours of stress distribution of gear shaft

图6　齿圈应力分布云图Fig.6　Contours of stress distribution of ring gear

3.3动力学分析

3.3.1齿轮轴、齿圈及壳体模态分析

低噪声海水泵是一种典型的旋转机械，工作中各零件在周期载荷的作用下必然会产生受迫振动。尤其是当激振力的激发频率等于或接近零件的固有频率时，将发生结构的共振，进而引起强烈的振动噪音和结构破坏［12］。以齿圈中心轴为 Z向，建立3D坐标系XYZ。文中利用模态分析模块对齿轮轴、齿圈和壳体进行模态分析，得到了各零件其前 5阶模态频率与模态振型，得到的模态频率见表 1，各零件的第 1阶模态振型分别见图7～图9。

按照低噪声海水泵工况，激振力基频在383.5～684.7 Hz之间。齿轮轴、齿圈和壳体最低阶模态频率均远大于激振力的激发频率，因此不会出现由于输入轴转矩引起的共振现象。

3.3.2齿圈谐响应分析

低噪声海水泵工作过程中，齿圈受到齿轮轴施加于齿面上的周期力的作用。持续的周期载荷作用于结构上将产生持续的周期响应［9］。文中利用ANSYS Workbench谐响应分析模块计算齿圈在动态载荷下的振动响应，ANSYS Workbench谐响应分析采用完全法和模态叠加法。模态叠加法又叫振动叠加法，它以系统无阻尼的模态（振型）为基底，通过坐标变换使式（6）解耦，进而通过叠加各阶模态的贡献以求得系统的响应［8］。

按照低噪声海水泵转速及负载设置齿圈啮合面所受的法向周期载荷幅值F=7 422 N。在齿轮啮合过程中齿圈振动响应起主要作用的是低阶模态，所以设定载荷激振频率范围100～7 000 Hz。

通过谐响应分析，得到齿圈外表面 X向、Z向以及某一齿面X向、Z向的振动响应。分别见图10～图13。

表1　各零件的前3阶模态频率Table 1　Modal frequencies of first three orders of components

图7　齿轮轴第1阶模态振型Fig.7　First-order modal vibration of gear shaft

图8　齿圈第1阶模态振型Fig.8　First-order modal vibration of ring gear

图9　壳体第1阶模态振型Fig.9　First-order modal vibration of shell

图10　齿圈外表面X向响应曲线Fig.10　Stress response curve in X direction on outer surface of ring gear

图11　齿圈外表面Z向应力响应曲线Fig.11　Stress response curve in Z direction on outer surface of ring gear

通过谐响应分析可知:

1） 齿圈外表面X向、Z向及齿面X向、Z向均在频率为1 900 Hz、5 100 Hz左右出现应力响应峰值，与齿圈模态频率一致；

2） 齿圈外表面在1阶模态频率附近X向应力响应最大值为941 MPa，齿面在2阶模态频率附近X向应力响应最大值为1 280 MPa；

3） 低噪声海水泵在实际工作中齿圈所受周期载荷的激发频率均在700 Hz之内，远小于齿圈的1阶模态频率，在此范围内齿圈应力响应值均在1 MPa以内。

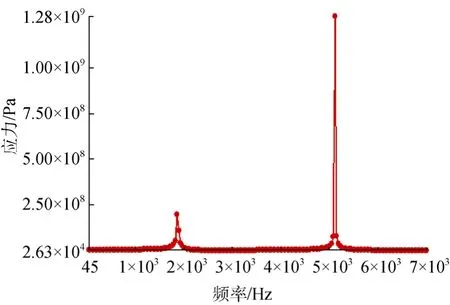
图12　齿面X向应力响应曲线Fig.12　Stress response curve in X direction on tooth surface

图13　齿面Z向应力响应曲线Fig.13　Stress response curve in Z direction on tooth surface

4　结论

文中利用ANSYS Workbench对低噪声海水泵关键零部件进行了静力学与动力学仿真，获得了泵在仿真现实工况下的力学特性，通过仿真分析得出如下结论:

1） 仿真得到了齿轮轴、齿圈应力分布情况以及两者啮合过程中的接触应力分布情况；

2） 通过模态分析得到了齿轮轴、齿圈、壳体等各自的振动固有频率值及模态振型，分析可知，泵在工作中不存在由于输入转矩引起的共振问题；

3） 通过对齿圈的谐响应分析得到了齿圈的应力响应曲线，从而预测齿圈在动载荷作用下的持续动力学特性。

［1］ 查志武，史小峰，钱志博.鱼雷热动力技术［M］.北京:国防工业出版社，2009.

［2］ 白坤雪，尹韶平.基于HyperMesh和Nastran的鱼雷海水管有限元分析［J］.鱼雷技术，2012，20（1）: 14-18.Bai Kun-xue，Yin Shao-ping.Finite Element Analysis for Torpedo Seawater Pipe Based on HyperMesh and Nastran［J］.Torpedo Technology，2012，20（1）: 14-18.

［3］ 李壮云.液压元件与系统［M］.北京: 机械工业出版社，2011.

［4］ 李宏伟，张方晓.内啮合齿轮泵齿形干涉分析［J］.机床与液压，2006（3）:135-136.Li Hong-wei，Zhang Fang-xiao.Research of Interal Gear Pumps Tooth Shape Interference［J］.Machine Tool & Hydraulics，2006（3）: 135-136.

［5］ 李兵，何正嘉，陈雪峰.ANSYS Workbench设计、仿真与优化［M］.北京: 清华大学出版社，2008.

［6］ 罗骥，吴盛林，袁子龙.水液压内啮合齿轮泵的设计与制造［J］.南京理工大学学报，2006，30（6）: 693-696.Luo Ji，Wu Sheng-lin，Yuan Zi-long.Design and Manufacture of Water Hydraulic Internal Gear Pump［J］.Journal of Nanjing Universtity of Science and Technology，2006，30（6）: 693-696.

［7］ 张国贤.高压内啮合齿轮泵［J］.流体传动与控制，2011，49（6）: 57-58.

［8］ 陈玲利.工程结构动力学分析数值方法［M］.西安: 西安交通大学出版社，2006.

［9］ 张亮，彭敬辉，李松晶.喷嘴挡板伺服阀力矩马达振动特性的谐响应分析［J］.机电工程，2012，29（12）: 1436-1438.Zhang Liang，Peng Jing-hui，Li Song-jing.Harmonic Response Characteristics of a Hydraulic Servo-valve Torque Motor［J］.Journal of Mechanical & Electrical Engineering，2012，29（12）: 1436-1438.

［10］ 凌桂龙，丁金滨，温正.ANSYS Workbench13.0从入门到精通［M］.北京: 清华大学出版社，2012.

［11］ 赵先锋，史红艳，何林.微小型齿轮副啮合过程的动态接触研究［J］.机械传动，2012，36（12）: 35-38.Zhao Xian-feng，Shi Hong-yan，He Lin.Research on Dynamic Contact of Mico Gear Meshing Process［J］.Journal of Mechanical Transmission，2012，36（12）: 35-38.

［12］ 倪振华.振动力学［M］.西安: 西安交通大学，1989.

（责任编辑: 陈曦）

Finite Element Analysis of Low-Noise Seawater Pump Based on ANSYS Workbench

LI Yong-dong，ZHANG Hai-ying，MA Xiao-lu，BAI Kun-xue，GAO Ai-jun
（The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710077，China）

Finite element method is applied in static and dynamic analyses of low noise seawater pump′s key components for a torpedo.The force and vibration characteristics of the key components in specific conditions are acquired through ANSYS Workbench，and the continuing dynamic characteristics of ring gear are predicted through harmonic response analysis.This study may provide a theoretical support for design and test of low noise seawater pumps，and is helpful for shortening development period，saving costs and improving design quality.

torpedo；low noise seawater pump；vibration characteristic；harmonic response；finite element analysis

TJ630.32；TH137.51

A

1673-1948（2016）03-0217-05

10.11993/j.issn.1673-1948.2016.03.011

2015-10-24；

2016-05-06.

李永东（1982-），男，硕士，工程师，主要研究方向鱼雷热动力技术.