近水面小型水下航行器鲁棒反推滑模深度控制

邵志宇，王雅捷

（北京理工大学 爆炸科学与技术国家重点实验室，北京，100081）

近水面小型水下航行器鲁棒反推滑模深度控制

邵志宇，王雅捷

（北京理工大学 爆炸科学与技术国家重点实验室，北京，100081）

小型水下航行器的近水面运动状态易遭受波浪扰动影响，致使其航行控制精度降低。为抑制波浪干扰，在建立小型水下航行器纵向模型的基础上，应用鲁棒反推滑模控制方法设计了深度控制器，建立了近水面波浪扰动模型和深度控制仿真模型，采用Matlab/Simulink对深度控制方法进行了仿真。仿真结果表明，所设计的控制器超调量小，调整时间短，鲁棒性强，在实际应用中易于实现。该研究为解决小型水下航行器深度控制中的波浪干扰问题提供了理论依据和技术支撑。

小型水下航行器；近水面；波浪扰动；鲁棒反推滑模控制

0　引言

小型水下航行器在执行既定的岸上监测任务时，将会在近水面定深航行，此时航行器将不可避免的受到近水面波浪的干扰作用，加之小型水下航行器本身质量较小，数学模型又是强耦合、高度非线性的，所以很容易受到近水面波浪的干扰作用，导致航行器运动稳定性降低，控制精度变差。因此设计一种有效的控制方法来抑制波浪干扰，满足航行器运动的快速性和稳定性具有重要意义。

近年来，国内外学者研究了许多抑制波浪干扰的控制方法。沈建森在考虑1阶波浪干扰的基础上，运用模糊滑模控制方法，设计出了自主水下航行器（autonomous underwater vehicle，AUV）的纵向运动控制器［1］，它虽然解决了 1阶波浪力扰动引起的控制输入高频抖动问题，但是系统响应速度慢，稳态精度不高。文献［2］采用基于AUV非线性扩张状态观测器的控制系统设计，较好地解决了未建模扰动以及参数摄动等问题，抗干扰能力较强，控制精度较高。文献［3］通过适当的假设对纵向模型进行了降阶，根据 H∞鲁棒控制适用于解决非结构不确定性问题的特点设计了AUV H∞混合灵敏度深度控制器，并与采用基于线性最优二次型高斯（linear quadratic Gaussian，LQG）理论设计的LQG控制器和 H2/H∞混合方法设计的控制器进行了对比，仿真结果表明，H∞混合灵敏度控制器具有更好的灵敏度，但由于其控制器阶数很高，按照某些方法降阶［4］后达不到预定精度，在实际应用中难以实现。反推滑模变结构控制将滑模控制与反推控制有机结合，兼具滑模控制对系统匹配不确定性的完全鲁棒性与反推控制可以有效处理系统中的非匹配不确定性，使控制系统对于匹配和不匹配不确定性均具有鲁棒性［5］。

文中建立了小型水下航行器的纵向运动数学模型，并将其作了部分简化，同时采用波谱理论与波浪力和力矩幅值响应理论建立了近水面1阶和 2阶波浪干扰模型，并利用鲁棒反推滑模变结构控制方法设计了航行器纵向运动的深度控制器，最后结合波浪扰动模型进行了仿真研究，仿真结果表明，所设计的控制器控制效果良好，抗干扰能力强。

1　水下航行器纵向系统模型

小型水下航行器的数学模型建立在2个坐标系下，一是体坐标系 Oxyz，原点为小型水下航行器的质心O，x轴沿航行器纵轴并指向前进方向，y轴垂直于x轴并指向右，z轴、x轴和y轴构成右手直角坐标系；二是惯性坐标系Oexeyeze，选用北东地（NED）坐标系，原点位于零时刻航行器质心的正上方水平面上。

航行器非线性模型由动力学模型和运动学模型组成。针对左右对称的小型水下航行器，其六自由度运动可分解成2个不耦合或弱耦合的子系统。这里u，v，w，p，q，r分别表示固定在航行器上的广义速度量；z表示深度；φ，θ，ψ表示相应的欧拉角即滚转角、俯仰角、偏航角；τ3，τ5为作用在小型水下航行器上的升沉力和俯仰力矩（包括舵力和波浪干扰力等），参数详见文献［6］。忽略v，p，r，φ的影响，并假设航行器以恒定速度u=u0航行，取w，q，z，θ为纵向运动参数，则可以得到小型水下航行器的纵向动力学方程

小型水下航行器纵向运动学方程

式中: a1，a2，b，w1，w2为转化后计算所得参数；δ为水平舵舵偏量；Zwave为波浪纵向干扰力；为波浪俯仰干扰力矩。

2　波浪扰动建模与仿真

波浪扰动模型的建立是基于对海洋领域各个分散模块的系统化整合，其建模思想见图 1。根据海洋状态建立波浪模型，然后对产生波浪的波幅进行叠加，并根据产生波浪的特征参数运用查表法获得幅值响应，最后求得六自由度波浪力和力矩。

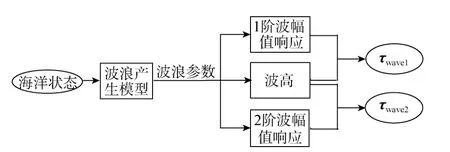
图1　波浪扰动模型框图Fig.1　Block diagram of wave disturbance model

图中，τwave1，τwave2分别为1阶波浪力、力矩向量和2阶波浪力、力矩向量。波浪产生模型是依据不规则波波谱建立的，由于建立过程涉及很多方面的内容，这里不再介绍，具体请参考文献［7］。

扰动模块的建模是基于对如下公式［8］的深入理解建立

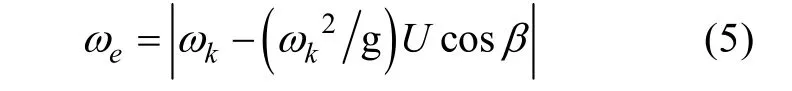
所以下一步的任务就是求取幅值响应。求取幅值响应的方法是借鉴文献［9］的计算公式。为了计算简便，不规则波的波浪力和力矩幅值响应可以通过求取规则波中波浪力和力矩响应来实现，即采用求取单位规则波波幅下的1阶波浪力和1阶波浪力矩

2阶波浪力和波浪力矩

1阶波浪力和力矩幅值响应采用影像平滑（smooth trans focus，STF）理论与Frank源分布理论相结合的方法来计算；2阶波浪力和力矩幅值响应采用Neman细长体方法，该方法要求航速不能太大，详细计算公式参考文献［10］。

为了提高模型的计算效率，文中采取有效措施即按照一定间隔选取可能出现的频率和方向，预先计算出其幅值响应（包括由此引起的相位响应），最后按照某种格式制作成表。实际使用时，只需按照线性插值法进行查表获得相应的幅值响应即可。

利用波浪扰动模型，在 2级海况下，对小型水下航行器1 m深处受到的1阶波浪力和力矩进行数学仿真，结果见图2和图3。可见，对于1阶波浪扰动最为明显的是垂荡力（即升沉力）和俯仰力矩，其他方向的力和力矩都很小，可近似忽略2阶波浪扰动在建模中忽略了和频力与倍频力，把它当作定常力来处理，只考虑其升沉力和俯仰力矩。

根据不同波浪等级情况，运用此波浪模型模拟产生的波浪力和力矩作为小型水下航行器所受外在干扰力，加入到系统仿真模型中，从而可以对不同波浪等级扰动下，小型水下航行器控制系统设计效果进行探究和评估。

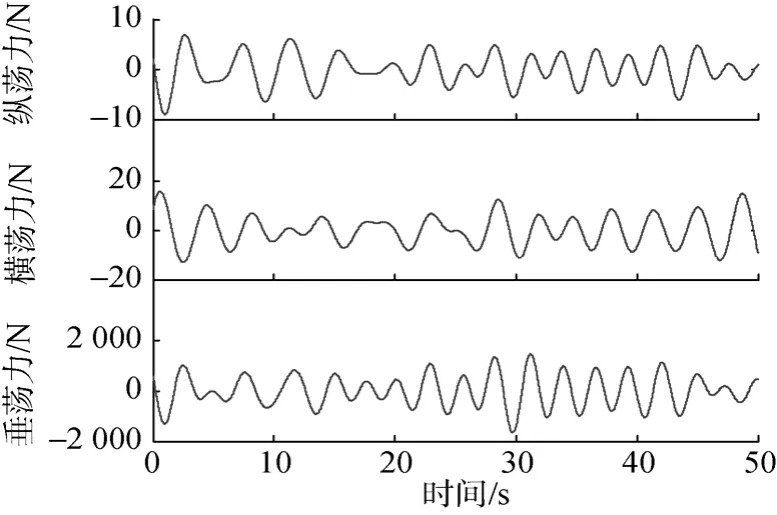
图2　1阶波浪力仿真曲线Fig.2　Simulation curves of first-order wave force

图3　1阶波浪力矩仿真曲线Fig.3　Simulation curves of first-order wave moment

3　鲁棒反推滑模变结构控制器设计

鲁棒反推滑模变结构控制是针对不确定性系统的一种系统化的非线性综合控制方法，是将Lyapunov函数的选取与滑动模态的设计相结合的一种变结构回归设计方法。它通过从系统的最低阶次微分方程开始，引入虚拟控制的概念，一步一步设计出满足要求的虚拟控制，并利用这些虚拟控制设计滑动模态，最终设计出真正的控制器。这种控制方法为复杂非线性系统的 Lyapunov函数设计提供了较为简单的结构化、系统化方法，解决了一直以来具有严格反馈等结构的非线性系统稳定性分析和控制器设计的难题。同时，变结构控制具有快速响应、对参数变化及扰动不灵敏，无需系统在线辨识，物理实现简单等优点。

考虑如式（3）的被控对象状态空间模型，采用3级反推滑模变结构控制方法设计深度控制器。假设高度指令为 zd，控制器设计步骤如下。

定义Lyapunov函数

定义

式中: c1为正常数；z2为虚拟控制项，且z2=，

定义第2个Lyapunov函数

第2步:

定义

式中: c2为正常数；z3是虚拟控制项，且 z3=故，可得，且

定义第3个Lyapunov函数

采用切换项抑制控制扰动，为保证V.3＜0，设计滑模控制律

将式（14）代入式（13）得

由于

所以只要保证Q为正定矩阵，则不管 s取何值都可使得

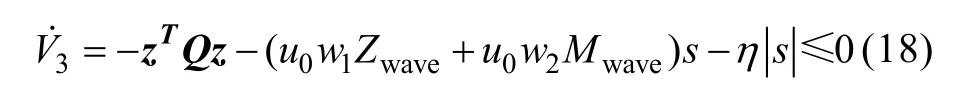
滑模变结构控制的1个缺点是抖振即滑模面两侧的频繁抖动的存在［11］。以往降低抖振的方法是用饱和函数sat（s）代替理想滑动模态中的符号函数sgn（s），这样可以减小抖振。

式中，Δ称为边界层。它的本质是: 在边界层外，采用切换控制；在边界层内，采用线性反馈控制。

4　仿真验证

文中针对文献［12］所设计的航行器进行仿真，主要特征参数如表1所示。

表1　航行器主要特征参数Table 1　Main characteristic parameters of an underwater vehicle

为验证文中所设计的控制器性能，在相同初始条件下，利用第 3节设计的控制器建立深度控制仿真模型，并在相同的模型下与线性二次型调节器（linear quadratic regulator，LQR）最优控制加以对比分析，分别以2种不同速度从2 m深度阶跃到1 m深度时的深度响应。

初始值设定如下: 航行器初始位置（x，y，z）= （0，0，2） m；初始姿态角（φ，θ，ψ）=（0°，0°，0°）；航速u=3 m/s和5 m/s；2级海况，遭遇角为30°。

图4为2级海况，遭遇角为30°时的波浪状态图。图 5和图 6分别为无干扰时航行器航速为5 m/s与3 m/s时深度控制阶跃响应。

图4　2级海况波浪状态图Fig.4　Diagram of wave state at second grade sea condition

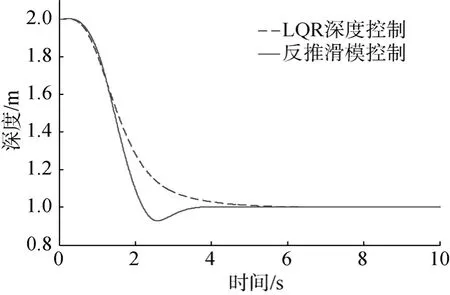
图5　5 m/s航速下无干扰时深度控制阶跃响应Fig.5　Step response of depth controller without disturbance when velocity is 5 m/s

图6　3 m/s航速下无干扰时深度控制阶跃响应Fig.6　Step response of depth controller without disturbance when velocity is 3 m/s

图7和图8分别为有干扰时航行器航速为5 m/s 与3 m/s时的深度控制阶跃响应。基于反推滑模变结构控制器在无干扰条件下快速稳定保持深度，且在近水面波浪扰动下，响应速度更快，稳态误差很小，具有较强的鲁棒性能，可以很好地满足小型水下航行器近水面纵向运动的控制精度；而 LQR最优控制在有干扰条件下，深度保持出现振荡，幅度相对较大，抗干扰能力较弱。

图7　5 m/s航速下有干扰时深度控制阶跃响应Fig.7　Step response of depth controller with disturbance when velocity is 5 m/s

图8　3 m/s航速下有干扰时深度控制阶跃响应Fig.8　Step response of depth controller with disturbance when velocity is 3 m/s

5　结束语

针对小型水下航行器在近水面运动时将受到波浪扰动，影响其运动稳定性和控制品质的问题，运用鲁棒反推滑模变结构控制方法设计深度控制器，建立了可以模拟现实波浪并能实时解算的波浪力和力矩仿真模型，并将其作为干扰加入到系统仿真模型中，验证了控制器的抗干扰能力的大小和控制效果的优劣。仿真结果表明，文中设计的控制器抗干扰能力强，控制精度高，响应速度快，可以有效抑制抖振，很好的完成小型水下航行器近水面纵向运动控制，为总体控制系统设计以及未来实航试验提供依据。

［1］ 沈建森，周徐昌，高璇.远程 AUV近水面运动纵向模糊滑模控制［J］.鱼雷技术，2011，19（5）: 360-364.Shen Jian-sen，Zhou Xu-chang，Gao Xuan.Fuzzy SlidingMode Control for Near-surface AUV in Longitudinal Plane［J］.Torpedo Technology，2011，19（5）: 360-364.

［2］ Li J，Kong M，Chen X H，et al.AUV Control Systems of Nonlinear Extended State Observer Design［C］//2014 IEEE International Conference on Mechatronics and Automation（ICMA）.Tianjin，China: IEEE，2014: 1924-1928.

［3］ Nag A，Patel S S，Kishore K，et al.Robust H-infinity Based Depth Control of an Autonomous Underwater Vehicle［C］//2013 International Conference on Advanced Electronic Systems（ICAES）.Pilani，India: IEEE，2013: 68- 73.

［4］ Feng Z，Allen R.Reduced Order H∞Control of an Autonomous Underwater Vehicle［J］.Control Engineering Practice，2004，12（12）: 1511-1520.

［5］ 王坚浩，胡剑波.不确定非线性系统的自适应反推高阶终端滑模控制［J］.控制与决策，2012，27（3）: 413-418.Wang Jian-hao，Hu Jian-bo.Adaptive Backstepping High-order Terminal Sliding Mode Conrol for Uncertain Nonlinear Systems［J］.Control and Decision，2012，27（3）: 413-418.

［6］ Fossen T I.Marine Control Systems: Guidance，Navigation and Control of Ships，Rigs and Underwater Vehicles ［M］.Trondheim，Norway: Marine Cybernetics AS，2002.

［7］ Asgeir J.Marine Control Systems: Propulsion and Motion Control of Ships and Ocean Structures［M］.Trondheim，Norway: Department of Marine Technology，NTNU，2012.

［8］ Fossen T I.TTK 4 190 Guidance and Control of Vehicles ［R］.Trondheim，Norway: Department of Marine Technology，NTNU，2011.

［9］ 吴秀恒，刘祖源，施生达，等.船舶操纵性［M］.北京:国防工业出版社，2005.

［10］ 戴遗山，段文祥.船舶在波浪中运动的势流理论［M］.北京: 国防工业出版社，2002.

［11］ 刘金琨.滑模变结构控制MATLAB仿真［M］.北京: 清华大学出版社，2005.

［12］ 孟凡豪.50 kg级水下自航行器整体水动力学性能优化设计［D］.杭州: 中国计量学院，2014.

（责任编辑: 杨力军）

Near-Surface Depth Control Based on Robust Backstepping Sliding Mode for Small Underwater Vehicles

SHAO Zhi-yu，WANG Ya-jie
（State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing 100081，China）

Near-surface motion state of a small underwater vehicle is influenced by wave disturbance to lower the control accuracy.To suppress wave disturbances，a longitudinal model of the small underwater vehicle was built in this study，and a depth controller was designed with the control method of robust backstepping sliding mode.A near-surface wave disturbance model and a depth control model were established to simulate the depth control method by using Matlab/Simulink.Simulation results show that the designed depth controller is easy to be implemented with small overshoot，short setting time and strong robustness.This study may provide theoretical and technical support for solving the problem of wave disturbance in depth control.

small underwater vehicle；near-surface；wave disturbance；robust backstepping sliding mode control

TJ630.33；TP273.1

A

1673-1948（2016）03-0200-06

10.11993/j.issn.1673-1948.2016.03.008

2016-03-18；

2016-04-21.

邵志宇（1974-），男，博士，副教授，主要研究方向为弹药制导控制.