双轴转台误差对加速度计标定精度的影响

曹雅丽，张福斌

（西北工业大学航海学院，陕西 西安，710072）

双轴转台误差对加速度计标定精度的影响

曹雅丽，张福斌

（西北工业大学航海学院，陕西 西安，710072）

自主式水下航行器（AUV）的水下导航精度主要取决于捷联惯导系统（SINS）的精度，文中对双轴位置转台误差（水平安装误差、水平仪调平误差、不正交安装误差等）进行了分析，将转台误差直接定义在转台误差坐标系中。根据已有的惯性器件误差模型，选定理想六位置的标定路径，得到重力加速度在转台误差坐标系中的真实投影值，并采用解析方法对含转台误差（尚未考虑各项误差之间的相互关系）的标定过程进行推导。通过设计合理的标定编排路径和有效的数学解析求解算法得到标定误差参数值的估计。仿真标定结果表明: 在短时间内可以验证标定方法的可行性，且标定误差参数值在合理的误差范围内，从而证明了含转台误差的标定路径编排算法的正确性。

自主式水下航行器（AUV）；双轴转台；加速度计标定；误差

0　引言

捷联惯性导航系统（strapdown inertial navigation system，SINS）广泛运用于自主水下航行器（autonomous underwater vehicle，AUV）的水下导航，其精度直接影响着AUV的导航精度。陀螺和加速度计是组成SINS的惯性器件（inertial measurement units，IMU），它们所引起的误差将会占到导航系统误差的70%以上。因此，IMU下水之前［1］通过标定实验确定出各项误差参数，是弥补SINS长期稳定性的有效途径，也是提高其精度的一种有效方法。

随着SINS精度的提高，转台对SINS标定精度会产生一定的影响。文献［2］从理论上推导了转台角位置基准误差与激光捷联系统标定结果之间的数学关系，分析了转台安装误差对加速度计零偏标定结果没有影响。文献［3］在标定过程中将转台旋转的内、外框角和不垂直度误差用四元数矩阵来表示，仿真分析得出水平误差对加速度计的影响很小，在角秒级内可以忽略。

文中主要考虑双轴转台误差对加速度计标定精度的影响，将转台误差直接详细地定义在转台误差坐标系中，根据六位置编排路径，得到重力加速度在转台误差坐标系中的真实投影值，从理论上推导了含转台误差矩阵的解析方法对标定结果的影响。同时，为了避免实际标定误差的影响，利用 MATLAB强大的仿真功能，通过对仿真标定路径的实现，得出的标定结果可以为实际的标定提供理论参考。

1　含转台误差的标定过程分析

1.1加速度计标定模型

采用简化的加速度计输出模型，仅考虑标度因数误差、安装误差及零偏［4-5］。

加速度计标定模型

1.2转台误差坐标系定义

对于双轴位置转台，其转动轴分别为转台主轴和转台俯仰轴；其中主轴可以 360°转动，俯仰轴仅能够±90°转动［6-7］。分析过程中涉及到3个坐标系: 转台坐标系p、惯组标定坐标系b、加速度计敏感坐标系a。

在利用双轴位置转台对加速度计标定时，需考虑的影响标定精度的误差项主要有以下几类。

第1类: 转台台面进行调平后，其与真实水平面之间的误差。该误差由俯仰轴的水平安装误差以及水准仪调平误差引起。

第2类: 转台转动过程中的角度测量误差。

第3类: 转台俯仰轴与主轴的不正交误差。

根据定义，p系相对于当地东北天地理坐标系n静止，且二者之间仅存在非常小的误差，误差之一为俯仰轴相对于真实水平面的安装误差，可视为角秒量级，记为δγp；误差之二为俯仰轴东西向的指向误差，在角分量级，记为δψp，则p系与n系之间的转换矩阵

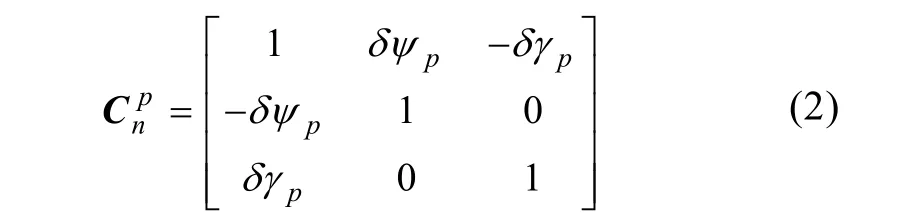
惯组标定名义坐标系b定义以转台主轴为基准，转台主轴定义为轴；，轴位于转台台面内，和zb构成右手正交坐标系。

根据上文定义，惯组标定名义坐标系b在标定初始时刻与转台坐标系 p间存在小的误差角，误差之一为转台俯仰轴与主轴的非正交误差，可视为角秒量级，记为δγb；误差之二为利用水平仪对转台台面进行调平时引入的调平误差，也为角秒量级，记为δθb，则b0系与p系间转换矩阵

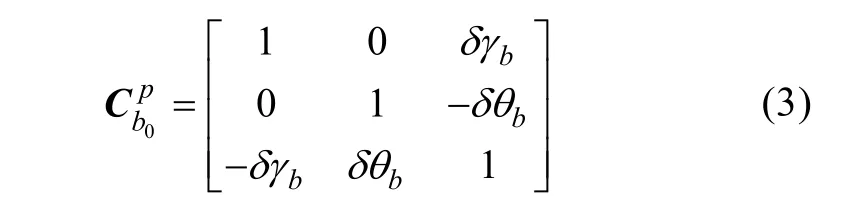
这样就可以得到标定起始位置上，参考输入在名义坐标系 b0上的真实投影。

1.3六位置标定路径的仿真分析

对标定模型（1）进行说明，IMU输出的是等式右端的脉冲数据，包含了IMU的测量噪声，是影响标定精度的因素之一。在计算时用的是名义坐标系上参考输入的名义值，而非真实值。

因为存在转台误差，所以，导致了在进行标定时，参考输入并不是真实输入，由此产生了额外的标定误差。

考虑转台误差时，将涉及标定方案中参考输入真值和名义值，以及SINS测量轴向的输入真值。实际标定算法是利用SINS的测量值和参考输入名义值来进行标定参数求解的；若利用SINS测量值和参考输入的真值来求解标定参数，则该求解结果就不受转台误差的影响。这2种求解方法所得到标定结果的偏差，即反应了转台误差对标定结果的实际影响。

1.4标定路径的编排算法推导

加速度计采用静态六位置标定方案［8-11］，当双轴位置转台的俯仰轴理想安装方向为东西向时，则静态标定六位置分别为: 东北天、西南天；东地北、东天南；地西北、天西南，且误差角可假定为1′～2′。

依据式（1），用六位置上的名义比力值代替等号右端的Na；用真实比力值代替等号左端的fb；此时若无转台误差，则标定参数矩阵Ka应为单位阵，零偏应为零值。但是由于存在转台误差，使得名义比力值和真实比力值不同，则会导致Ka偏离单位阵，而零偏也不会为零。对完成上述替换之后的式（1）两端首先进行转置，可得

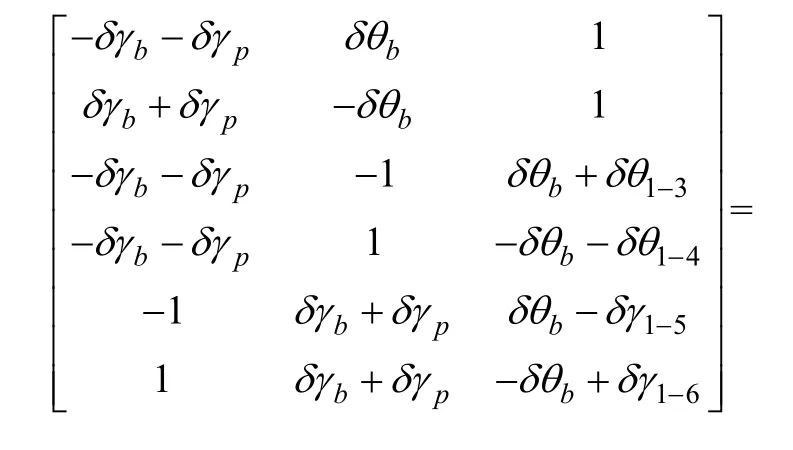
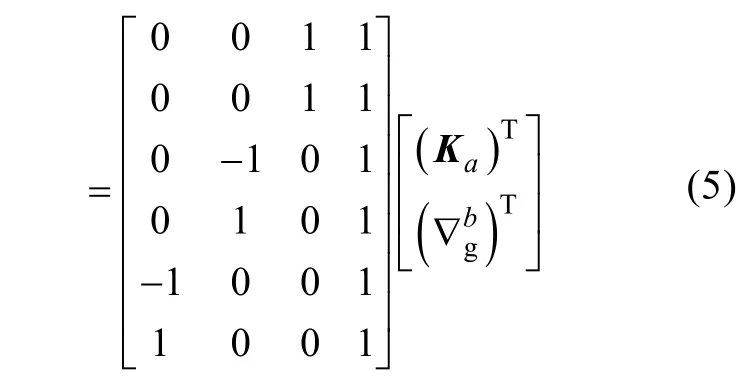
将式（5）中等号左端矩阵记为Fr，右端第1个矩阵记为F，将待求解参数构造的矩阵记为X，则X在标定算法中的最小二乘解为

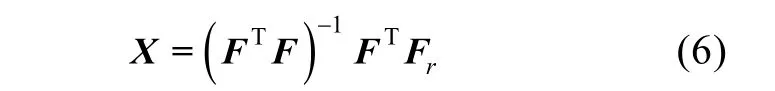
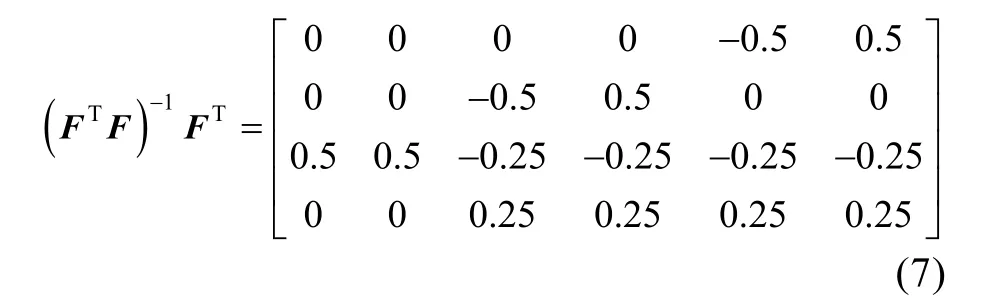
将Fr和（FTF）-1FT代入式（6）中，得

从而有零偏的标定误差为

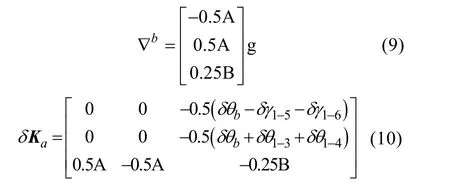
针对上述推导，给定典型的误差值，仿真计算得相关误差项，见式（11）。按照标定轨迹计算真实比力值，在不考虑噪声情况下，可得Ka和∇b。

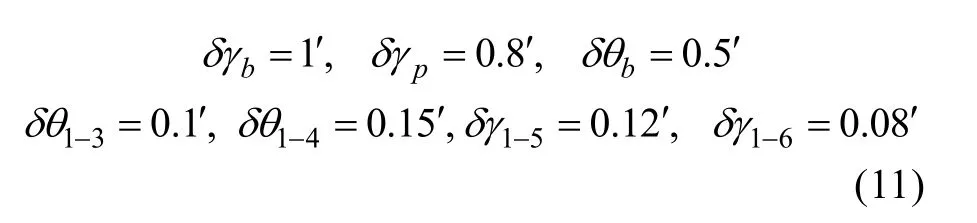
可知，式（9）和式（10）的推导过程与标定过程一致，因此，计算结果与理论分析值吻合。

由于实际系统均含有测量噪声，若进一步考虑IMU噪声的影响，设置加速度计测量噪声标准差为每个位置静止采数3 min，采样频率设为100 Hz。Ka和∇b分别为

对比增加噪声前后的计算结果，可知，通过对每个位置上的输出进行均值可以基本抑制噪声的影响，最终计算结果仍然主要由转台误差决定。

加速度计静态六位置标定，不同位置上标定坐标系上名义比力值、真实比力值的计算公式如下。

位置1（东北天），标定坐标系各轴名义比力值

标定坐标系各轴真实比力值

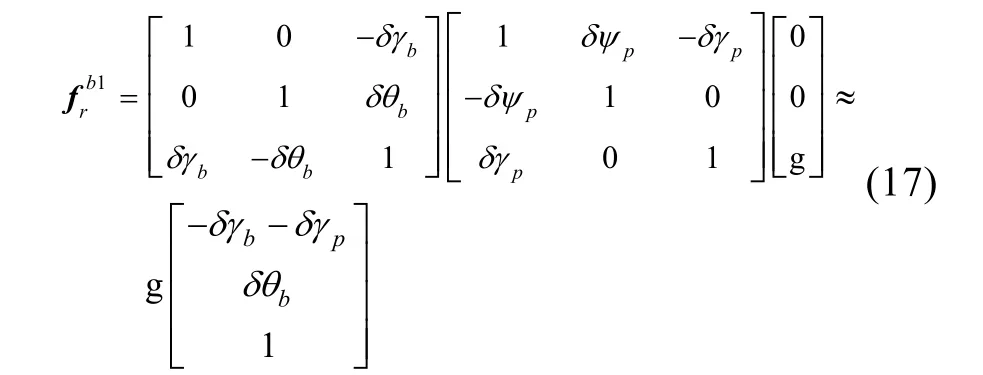
位置2（西南天）在实现上，认为是由位置1绕转台主轴转动180°得，此时需考虑转台的角定位误差。理想转动180°，实际转动角度的偏差记为δψ1- 2。

标定坐标系各轴名义比力值

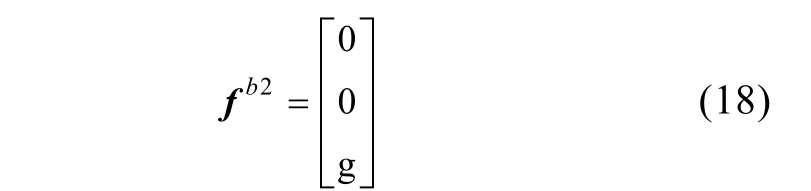
标定坐标系各轴真实比力值

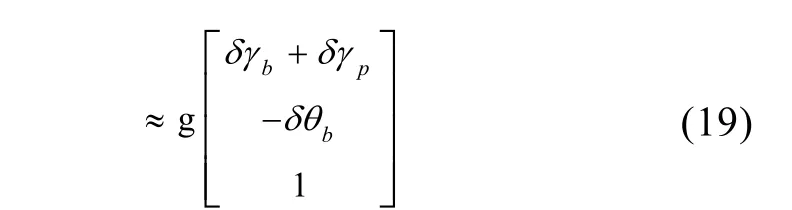
位置3（东地北）在实现上，认为是由位置1绕转台俯仰轴转动-90°得到，转动误差记为δθ1- 3。

标定坐标系各轴名义比力值

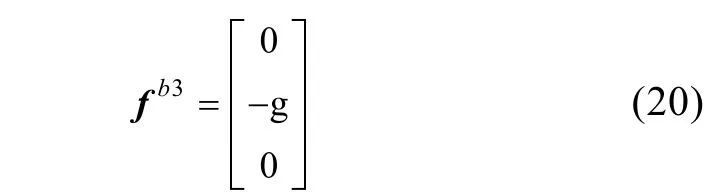
标定坐标系各轴真实比力值

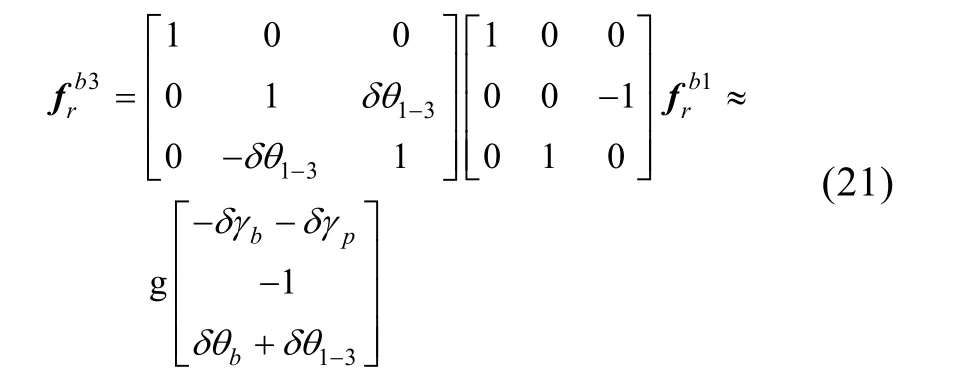
位置4（东天南）在实现上，认为是由位置1绕转台俯仰轴转动90°得到，转动误差记为δθ1- 4。

标定坐标系各轴名义比力值

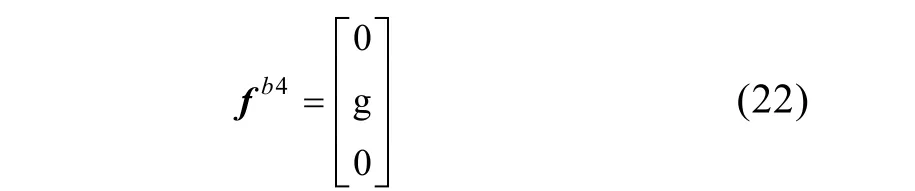
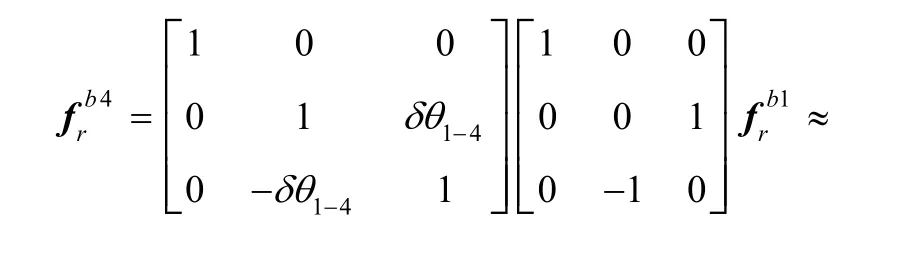
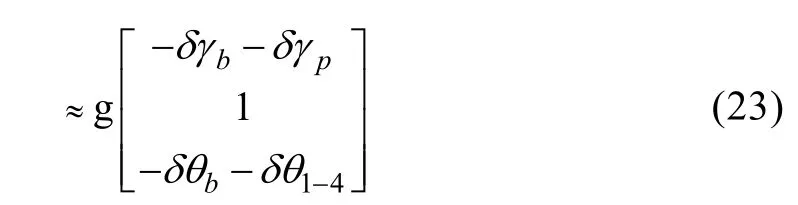
标定坐标系各轴真实比力值δψ-；然后绕着转台俯仰轴转动-90°得到，转动角误差记为δγ1- 5。

标定坐标系各轴名义比力值

位置5（地西北）在实现上，认为是由位置1首先绕着转台主轴转动90°，转动角误差记为1 5

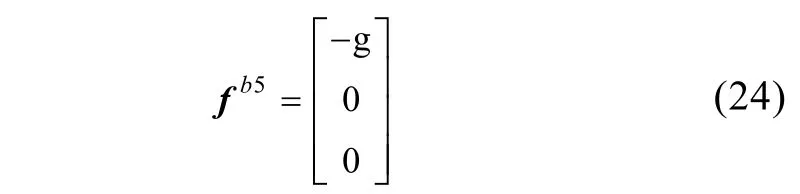
标定坐标系各轴真实比力值

位置6（天西南）在实现上，也需经过2次连续转动，第1次转动过程与位置5实现中第1次转动一致，即右位置1首先绕转台主轴转动90°；然后绕转台俯仰轴转动90°，转动角误差记为δγ1- 6。

标定坐标系各轴名义比力值

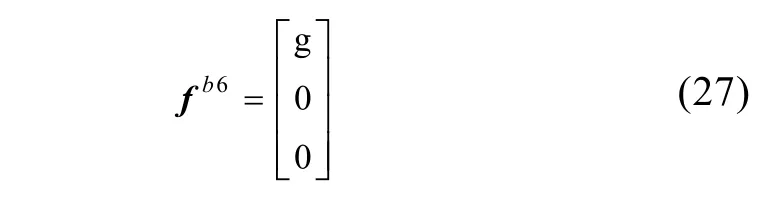
标定坐标系各轴真实比力值

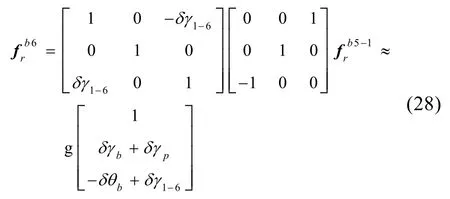
以上公式的推导均考虑了转台误差情况下，加速度计的真实激励解析表达式。

2　仿真结果与分析

根据转台误差标定模型，首先生成加速度计模拟的比力输入，再根据测量模型计算得到加速度计的输出，考虑双轴转台误差（水平安装误差、水平仪调平误差、不正交安装误差等），利用标定算法公式计算出加速度计各标定误差参数，与设置的标定误差参数值进行比较，见表1（表1和表2分别是设定的标定误差参数值和实际得到的标定值）。

表1　标定误差参数值设置Table 1　Setting of calibration error parameters

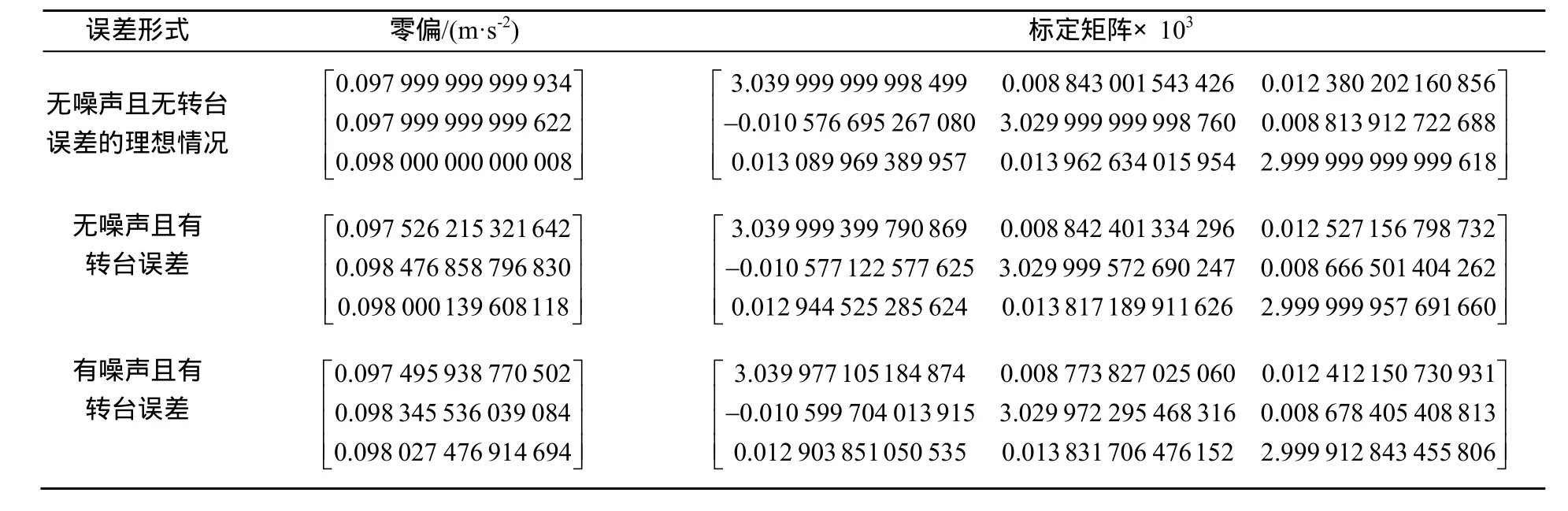
表2　仿真结果Table 2　Simulation results

加速度计转动到多个定角进行标定时，首先考虑计算由误差角所引起重力加速度的投影，然后利用原来的位置匹配计算方法进行参数计算，由于转台误差角真实存在，通过仿真分析其对标定参数值是否有影响，如表2所示［12］。

由仿真结果可得到以下结论:

1） 分析表2可知，转台各项误差对实际得到的标定参数值存在不同程度的影响；

2） 分别就无噪声且无转台误差，无噪声且有转台误差、有噪声且有转台误差这3种情况进行分析可知，设定的标定误差参数值和实际得到的标定值基本相同，转台误差（零偏误差、标定矩阵误差）对加速度计标定结果没有影响，其仿真验证与解析推导一致，计算可得标定误差参数值的绝对误差大小约为

3　结束语

依据标定的测试需要，阐述了含转台误差矩阵的推导方法。对双轴位置转台误差（水平安装误差、水平仪调平误差、不正交安装误差等）进行分析，利用 wat函数来设定加速度计的六位置标定路径。通过设定相对应的仿真参数，对实际的标定路径仿真，从理论上分析双轴转台误差对加速度计标定参数值的影响，仿真结果表明了 1.4节含转台误差的标定路径编排算法分析的正确性。

后续工作中，针对回转误差、相交度误差和各项误差之间相互关系的分析，以及在标定过程中，如何选取最优标定位置数来适当提高标定速度和标定精度等方面都有待进一步的展开。

［1］ 王立文，国琳娜.惯性测量装置标定技术研究［J］.鱼雷技术，2003，11（1）: 17-22.

［2］ 丁枫，冯丽爽，晁代宏，等.转台安装误差对光学捷联惯导标定的影响分析［J］.弹箭与制导学报，2013，33（1）: 19-24.Ding Feng，Feng Li-shuang，Chao Dai-hong，et al.The Influence of Turntable Fixing Errors on Optical Gyro Strapdown Inertial System Calibration［J］.Jounal of Projectiles，Rockets，Missiles and Guidance，2013，33（1）: 19-24.

［3］ 贾明，王振飞，晁代宏.双轴转台误差对 IMU标定精度的影响分析［J］.导航与控制，2012，11（2）: 68-72.Jia Ming，Wang Zhen-fei，Chao Dai-hong.Effects of the Two-axis Turntable′s Errors on the Accuracy of IMU［J］.Navigation and Control，2012，11（2）: 68-72.

［4］ 邓志红，刘亚辰，王清哲，等.转台角位置基准误差对激光捷联惯导标定的影响分析［J］.中国惯性技术学报，2009，17（4）: 489-504.Deng Zhi-hong，Liu Ya-chen，Wang Qing-zhe，et al.Influence of Truntable Angular Position Reference Errors on Laser SINS Calibration［J］.Journal of Chinese Intertial Technology，2009，17（4）: 489-504.

［5］ 张红良.陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究［D］.长沙: 国防科学技术大学，2010.

［6］ 康宇航，周绍磊，匡宇，等.高精度捷联惯导系统的系统级标定方法［J］.兵工自动化，2013，32（1）: 53-57.Kang Yu-hang，Zhou Shao-lei，Kuang Yu，et al.Systematic Calibration Method for High-precision Strapdown Inertial Navigation System［J］.Ordnance Industry Automation，2013，32（1）: 53-57.

［7］ 肖桂平，张红良，吕鸣，等.转台非正交度和不水平度误差对陀螺标定精度的影响分析［J］.系统仿真学报，2009，20（增）: 370-373.Xiao Gui-ping，Zhang Hong-liang，Lü Ming，et al.Effect of Turntable′s Orthogonal Error and Horizontal Error on Gyro Calibration Accacy［J］.Journal of System Simulation，2009，20（z）: 370-373.

［8］ Savage P G.Strapdown Analytics［M］.Maple Plain，Minnesota: Strapdown Associates，Inc，2007.

［9］ 严恭敏，秦永元.激光捷联惯组的双轴位置转台标定仿真［J］.中国惯性技术学报，2007，15（1）: 123-127.Yan Gong-min，Qin Yong-yuan.Calibration Simulation for Laser Strapdown IMU with Two-axis Turntable［J］.Journal of Chinese Intertial Technology，2007，15（1）: 123-127.

［10］ 肖桂平.光学陀螺捷联惯导系统的标定精度分析［D］.长沙: 国防科学技术大学，2008.

［11］ 谢波，秦永元，万彦辉.激光陀螺捷联惯导系统多位置标定方法［J］.中国惯性技术学报，2011，19（2）: 157-162.Xie Bo，Qin Yong-yuan，Wan Yan-hui.Multiposition Calibration Method of Laser Gyro SINS［J］.Journal of Chinese Inertial Technology，2011，19（2）: 157-162.

［12］ 梅春波.基于 MEMS惯性器件的应急地平仪研究［D］.西安: 西北工业大学，2010.

（责任编辑: 杨力军）

Effects of Two-axis Turntable Position Errors on Accelerometer Calibration Accuracy

CAO Ya-li，ZHANG Fu-bin
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

The accuracy of a strapdown inertial navigation system（SINS） directly determines the underwater navigation accuracy of an autonomous underwater vehicle（AUV）.In this paper，the two-axis turntable position errors（including horizontal installation error，gradienter leveling error，non-orthogonal installation error，etc.） were analyzed，and the turntable errors were defined directly in the turntable coordinate system.According to the existing of inertial device error model，six ideal position calibration paths were selected，real projection value of acceleration of gravity in the coordinate system was obtained，the calibration process with turntable error was derived by using analytic method（without considering the relationship between the errors），and calibration error estimation of parameter was accomplished through reasonable design of calibration path and effective mathematical algorithm.Simulation calibration results show that the proposed calibration method is feasible in a short time，and the calibration error parameter value is within the reasonable error range，which proves the correctness of the proposed calibration path scheduling algorithm.

autonomous underwater vehicle（AUV）；two-axis turntable；accelerometer calibration；error

TJ630.33；U666.12

A

1673-1948（2016）03-0194-06

10.11993/j.issn.1673-1948.2016.03.007

2016-03-18；

2016-05-25.

曹雅丽（1989-），女，硕士，主要研究方向为水下航行器导航与控制.