基于温度应力下鱼雷贮存寿命试验模型

张百勇，刘　凯，孙　炯，李宏胜，林　洋

（1.海军工程大学 兵器工程系，湖北 武汉，430033；2.海军工程大学 科研部，湖北 武汉，430033；3.海军东海舰队 装备部，浙江 宁波，315121）

基于温度应力下鱼雷贮存寿命试验模型

张百勇1，刘凯2，孙炯2，李宏胜3，林洋1

（1.海军工程大学 兵器工程系，湖北 武汉，430033；2.海军工程大学 科研部，湖北 武汉，430033；3.海军东海舰队 装备部，浙江 宁波，315121）

针对鱼雷贮存寿命评估问题，分析了影响鱼雷贮存寿命的主要环境因素，提出采用温度应力进行鱼雷加速寿命试验，在此基础上利用Arrhenius模型进行鱼雷贮存寿命评估，给出了加速寿命试验方法及Arrhenius模型参数的确定方法，并通过选取影响鱼雷贮存寿命的典型组件进行加速试验，验证了该模型的合理性。文中所作研究对鱼雷加速寿命试验和常温下贮存寿命的评估有一定的指导意义。

鱼雷；加速寿命试验；温度应力；Arrhenius模型

0　引言

鱼雷是主要的反舰、反潜武器，其性能的稳定与否直接关系着海军潜艇作战能力，在未来战争中发挥着不可替代的作用。鱼雷具有“长期贮存，一次使用”的特点，影响鱼雷贮存寿命的环境因素主要是温度和相对湿度，而鱼雷的贮存主要是库房贮存，一般都采用密封包装，透温不透湿。因此，影响鱼雷贮存寿命的主要环境因素为温度。贮存寿命是鱼雷重要的技术指标之一［1］，鱼雷超过实际寿命时其可靠性无法保证，未达到实际寿命而退役是对资源的一种浪费，那么选取恰当的模型和设计合理的试验来准确评估鱼雷的贮存寿命就显得尤为重要。

自然条件下贮存试验和实验室加速寿命试验这2种方法常被国内外学者用来估计产品的贮存寿命［2］。自然条件下贮存试验是指把影响鱼雷寿命的典型组件放在自然环境下，隔一定时间检测组件参数的变化，并根据检测结果来估计鱼雷寿命的一种方法，这种方法真实性高，但时间长，不易实现。加速寿命试验是在失效机理不变的基础上，通过寻找产品寿命与应力之间的物理化学关系，利用高加速应力水平下的寿命特征外推或评估正常应力水平下的寿命特征的试验技术和方法，所需时间可大大减少。

文中针对影响鱼雷贮存寿命的主要因素，基于Arrhenius加速方程，对鱼雷贮存加速寿命试验模型进行了假设，用图表法和最小二乘法分析鱼雷典型组件加速寿命试验数据，验证了该模型的合理性，推出鱼雷在常温下的贮存寿命，文中所作研究可用于指导鱼雷贮存加速寿命试验实施。

1　常见的加速模型

为了达到利用加速寿命试验中搜集到的产品寿命信息，实现外推产品在正常应力下的寿命特征目的，必须建立产品寿命特征与加速应力水平之间的物理化学关系，即加速模型。

1.1Arrhenius模型

Arrhenius模型常用于描述温度加速应力与产品寿命特征之间的关系［3］，即

其中: η为特征寿命；T为热力学温度，它等于摄氏度加273.15 K；A为与失效模式、加速试验类型及其他因素相关的常数；k为波尔兹曼常数，为8.617×10-5eV/K；Ea为激活能，或称为活化能，单位是电子伏特，以eV表示，他们都是待定参数。

1.2逆幂率模型

当环境因素为电应力（如电压、电流、功率等）作为加速应力时，产品寿命特征与这些应力之间满足下列关系［3］

其中: A为一个正常数；c为一个与激活能有关的正常数；V为应力，常取电压。

1.3Eyring模型

当环境应力一个为温度，另一个为除温度之外的应力时，一般认为产品寿命特征与温度之间的关系满足下式［3］

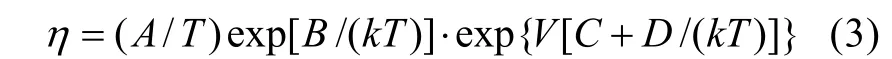
其中: A，B，C，D可通过加速试验数据分析进行估计的待定常数；T，V为2种加速应力水平。

1.4复合应力加速模型

当环境应力有多个时，可认为产品寿命特征与应力之间的关系满足下式［4］

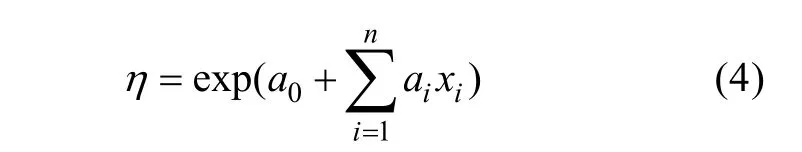
其中: ai为位置参数；xi表示第i个环境应力；a0为常数。

2　试验模型的构建

鱼雷在贮存过程中，表面和内部都会发生缓慢的物理和化学变化，这些变化增大到一定程度时就会使鱼雷各组件发生失效，而鱼雷各组件所受各种应力的大小决定了这些物理、化学变化的速率［5］。根据反应论模型［6］的定义可以看出，鱼雷各组件无论在一般状态下还是在寿命加速试验状态下都和 Arrhenius模型有很多相似之处。因此，在温度应力下，以Arrhenius加速方程为基石，建立鱼雷贮存加速寿命试验模型。

2.1模型初建

假设在正常应力水平T0和k个不同温度应力水平 T1＜T2…＜Tk下，鱼雷贮存寿命服从威布尔（Weibull）分布［7］，即

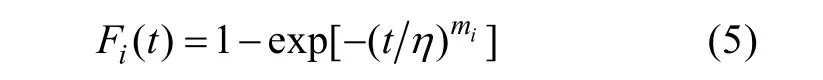
式中: t为时间；mi＞0（i=1， …，k）为形状参数；ηi＞0 （i=1， …，k）为特征寿命。

鱼雷在不同温度应力水平T1＜T2…＜Tk下的失效机理与正常应力水平T0下的失效机理相同。由于威布尔形状参数反映了失效机理的变化，因此意味着，所有应力水平下的威布尔分布中形状参数mi保持不变，即

鱼雷的特征寿命ηi与温度应力水平Ti之间符合Arrhenius加速方程，即

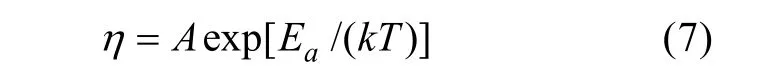
对此模型两边取对数，得到线性化的 Arrhenius模型，即

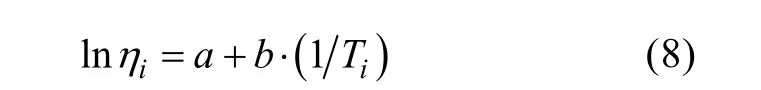
式中: a，b为常数，a=lnA，b=Ea/k。

2.2贮存加速寿命试验模型

声自导和引信在鱼雷贮存寿命［8］中起着关键作用，而声自导和引信主要由机械组件、电子组件、机械电子组件等部件串联而成，由文献［1］可知他们的寿命分布符合假设的威布尔分布。在保证失效机理不发生改变的前提下，适当增加试验温度，可以加快试验进程，试验结束后，对产品的失效数和失效时间进行数据处理，由式（8）可以求出参数a，b，从而得出鱼雷的贮存寿命。因此，将式（8）作为鱼雷贮存加速寿命试验模型是可行的。

3　确定试验参数

根据不同变化形式的应力，加速寿命试验应力施加方式通常分为3种: 恒定应力、步进应力和序进应力［7］。考虑到试验操作的简易性，文中采用恒定应力加速寿命试验法。

1） 应力量值的选取［9］。温度应力量值的选取应综合考虑鱼雷关键组件的设计特点、电路板和元器件的贮存温度范围、原材料和辅料的耐温范围等3个主要因素。试验应力量值的选取不宜过低或过高，试验应力量值过低将导致试验受试产品的加速效应不明显，反之，则会使试验受试产品失效机理发生改变，甚至损伤试验受试产品，这2种情况都达不到加速试验的目的。

根据上述原则，分别选取 4个温度应力为T1=323 K，T2=333 K，T3=343 K，T4=353 K。

2） 检测项目。检测项目的选取要考虑影响鱼雷贮存寿命的典型组件，声自导探测准确性和引信可靠性对鱼雷整体性能有决定性作用，可以作为检测项目。

3） 检测时机。考虑到鱼雷实际贮存中通常定期检测的周期为 0.5年，根据加速因子计算出等效贮存 0.5年所需的试验时间作为检测间隔，试验开始后，每隔一个检测间隔检测一次。在试验中，按规定的检测时间点将受试产品恢复到常温后进行检测。

4） 确定试验结束时间。试验结束时间的确定通常要考虑两方面的因素: 性能参数退化规律和失效数［1］。由于用测试性能参数退化规律试验的方法来确定结束时间没有统一的标准，并且实现难度较大，因此文中采用测试失效数试验的时间作为试验结束时间，当试验样品出现 1/4失效数时，试验结束，此时的时间为试验结束时间。

5） 试验样品必须在各方面检测均合格的产品中随机抽取，样本量的选取既要兼顾试验的成本，又要保证统计分析的正确性。本次试验有 4个不同温度应力，每个温度应力进行 4组试验，每组12个样本量，总共所需样本数量为192个。

4　试验步骤

高低温试验箱是加速寿命试验最常用的仪器设备，试验之前按照相关规定做好安全防护措施。试验步骤: 1） 调制试验箱分别为50℃、60℃、70℃和80℃，温差控制在±2℃；2） 按上述方法分装样本，每组12个，放进试验箱内，1.5 h后开始计时；3） 当到达试验结束时间时，随机抽取试验箱中的样本按照第3章中确定的检测项目进行检验。

试验中开关试验箱门时应在尽可能短的时间内完成，以保证试验箱内的温度不会发生太大的变化，抽取的样本要等恢复到常温再检测。

5　试验数据处理方法

统计、分析试验数据，用图表法和最小二乘法处理试验数据，外推或计算出常温下鱼雷的寿命终止时间。

5.1图表法

1） 平均寿命终止时间。根据不同温度应力水平下鱼雷的失效时间不同，可以得出每个温度下鱼雷的平均寿命终止时间tzi。

2） 温度加速寿命直线。以1/Ti为横坐标，lntzi为纵坐标，根据试验数据依次在单对数坐标纸上描点，合理画出一条直线，即为温度加速寿命直线，如图1所示。

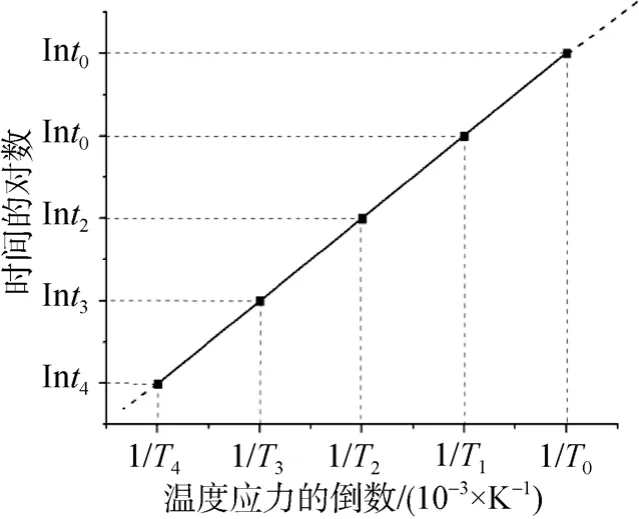
图1　温度加速寿命试验Fig.1　Temperature accelerated life test

5.2最小二乘法拟合曲线方程

根据试验获取的数据（1/T1，lntz1），（1/T2，lntz2），（1/T3，lntz3），（1/T4，lntz4），用最小二乘法拟合曲线，估计出常数 a，b，则温度加速寿命方程［10］为

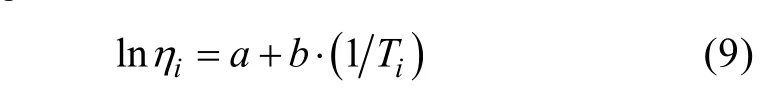
将T0代入，有

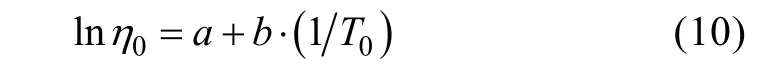
有

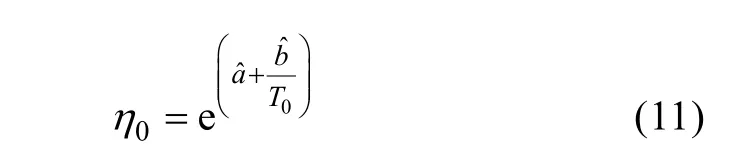
再根据式（5）即可求出常温下鱼雷的贮存寿命tz0。

6　试验结果与分析

根据上述方法，对鱼雷进行加速寿命试验，分析试验数据，在置信度为γ和最低可接受值为RL的条件下，计算出鱼雷常温下的贮存寿命，看是否满足作战使用要求。表1为加速寿命试验数据。

由上述假设的鱼雷寿命服从威布尔分布，则由分布函数得出鱼雷可靠度函数为

式中: mi为形状参数，等式两边取二次对数运算，得

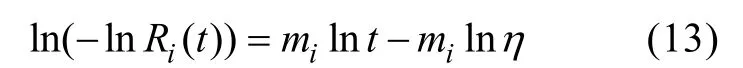
由式（13）可得: 当mi为常数时，与 lnt成线性关系，由试验数据可以画出温度应力T为323 K，333 K，343 K下拟合的可靠度与鱼雷寿命的关系曲线如图2所示。

图2中L1, L2, L3分别为323 K, 333 K, 343 K温度应力下由试验数据拟合得出的直线，直线的斜率为威布尔分布中形状参数m，分别为m1，m2，m3。

根据试验要求，在误差允许的范围内，满足m1=m2=m3，可以验证假设的正确性，即，在本次试验温度应力水平下，鱼雷的失效机理未发生改变。

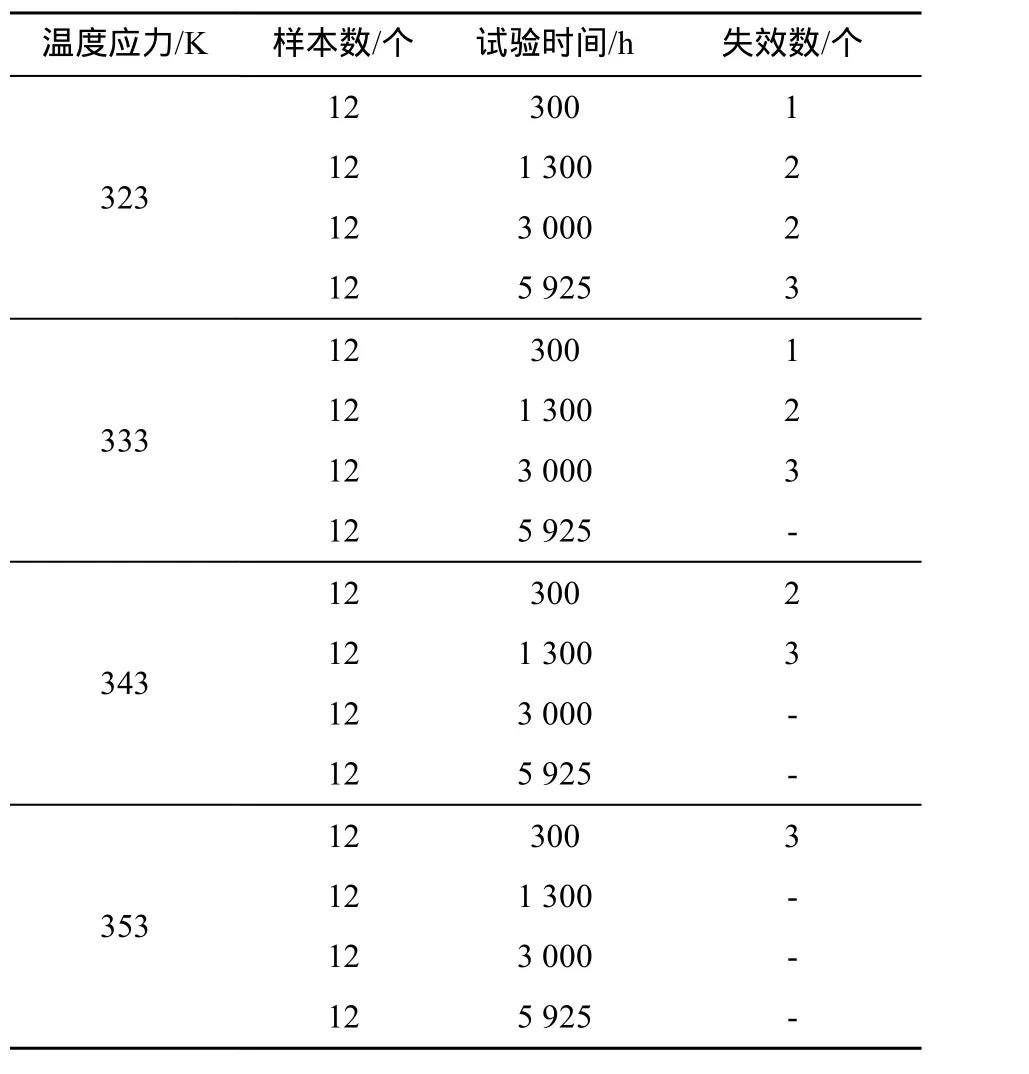
表1　加速寿命试验数据Table 1　Data of accelerated life test

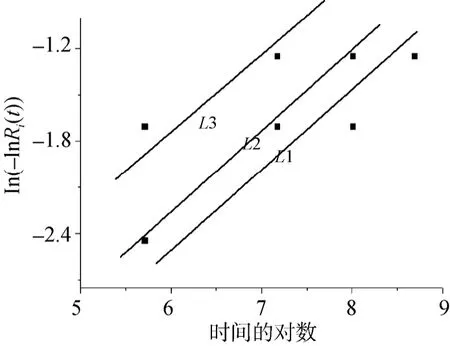
图2　拟合的可靠度与寿命关系曲线Fig.2　Relationship between fitting reliability and life

根据表1数据，当γ=0.75时，由5.2节的方法拟合出的加速寿命方程为是枢轴量V（R）上α分位数。式中:是

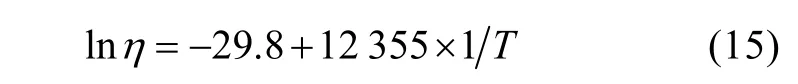
由式（12）、式（14）和式（15）计算，可以求出鱼雷在常温状态下 293 K（20℃ ）的贮存寿命 tz0为26.1a（RL=0.85）。图3为温度和寿命的关系曲线。

图3（a）中横坐标代表温度应力的倒数 1/T，纵坐标表示鱼雷每组试验的寿命终止时间 t，通过曲线可以看出，随着温度应力的不断增大（1/T的减小），鱼雷的寿命终止时间 t也会随之减小，满足威布尔分布模型的特点。图3（b）中横坐标与图 3（a）横坐标相同，纵坐标是对寿命终止时间取自然对数lnt，鱼雷的加速寿命方程就可通过最小二乘法拟合出。根据式（15），即可求出鱼雷在常温下293 K（20℃）时的贮存寿命tz0为26.1a。

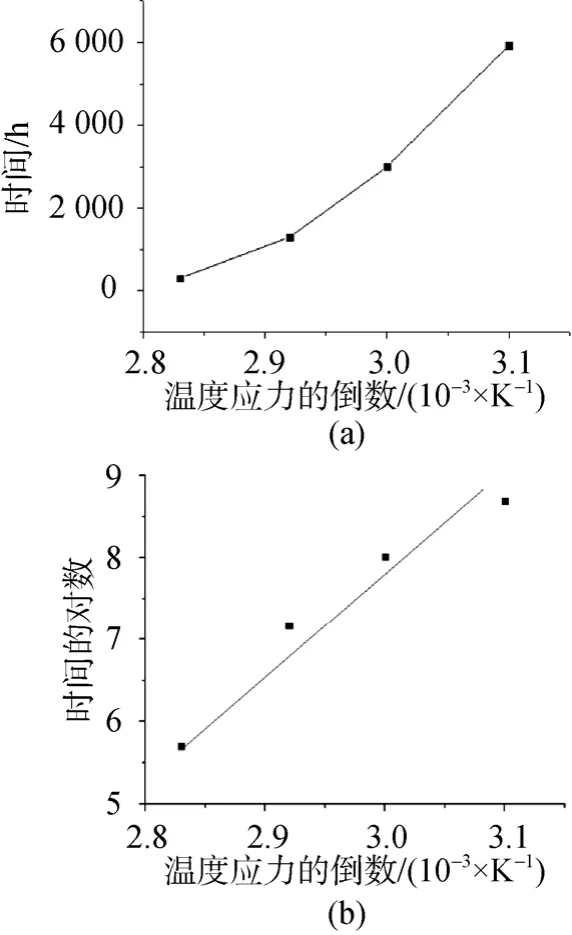
图3　温度和寿命的关系曲线Fig.3　Relationship between temperature and life

7　结束语

文中基于温度应力水平对鱼雷的贮存加速模型进行了假设，通过不同温度应力水平的鱼雷贮存加速寿命试验得出数据，用图表法和最小二乘法对试验数据进行分析、拟合，验证了在本次试验温度应力水平下，鱼雷的失效机理未发生改变，以及鱼雷寿命与温度应力的关系满足假定的威布尔分布，进而外推出常温下鱼雷的贮存寿命。该方法简单易行，对鱼雷贮存寿命试验有一定的借鉴意义。但Arrhenius模型中激活能以及加速方程中加速因子的确定等方面还需要进一步论证。

［1］ 李琛，邵宗战，张姝红，等.基于恒定应力加速寿命试验法评估深弹贮存寿命［J］.科技导报，2009，27（20）: 87-90.Li Chen，Shao Zong-zhan，Zhang Shu-hong，et al.Life Estimation of Deep Bomb Storage Based on Constant Stress Accelerated Life Testing［J］.Science &Technology Review，2009，27（20）: 87-90.

［2］ Mohammed A E，Higgins J J.Non-parametric Analysis of a Proportional Wearout Model for Acceleration Data［J］.Aliped Mathematics&Computation，2006，174（1）: 365-373.

［3］ 姜同敏.可靠性与寿命试验［M］.北京: 国防工业出社，2012.

［4］ 文建国，郭桂友.弹上电子产品加速寿命试验设计与应用［J］.舰船电子工程，2013，33（2）: 99-101.Wen Jian-guo，Guo Gui-you.Design and Application of the Accelerated Life Test on Electronic Products of Missile［J］.Ship Electronic Engineering，2013，33（2）: 99-101.

［5］ 姜仁元，张兴唐，杨亦春.温度应力下功能退化型加速寿命试验问题研究［J］.南京理工大学学报，2000，24 （6）: 523-527.Jiang Ren-yuan，Zhang Xing-tang，Yang Yi-chun.Study on Accelerated Life Test of Function Degenerating Type by Temperature Stress［J］.Journal of Nanjing University of Science and Technology，2000，24（6）: 523-527.

［6］ 刘强，周经伦，金光，等.基于随机阈值的 Gauss Brown失效物理模型的动量轮可靠性评估［J］.宇航学报，2009，30（5）: 2109-2115.

［7］ 张志华.加速寿命试验及其统计分析［M］.北京: 北京工业大学出版社，2002.

［8］ 中国人民解放军总装备部电子信息基础部标准化研究中心.GJB2166-1994鱼雷贮存要求［S］.北京: 中国人民解放军总装备部，1994.

［9］ 申争光，苑景春，董静宇，等.弹上设备加速寿命试验中加速因子估计方法［J］.系统工程与电子技术，2015，37（8）: 1948-1952.Shen Zheng-guang，Yuan Jing-chun，Dong Jing-yu，et al.Research on Acceleration Factor Estimation Method of Accelerated Life Test of Missile-borne Equipment［J］.Systems Engineering Electronic，2015，37（8）: 1948-1952.

［10］ 张志华.可靠性理论及工程应用［M］.北京: 科学出版社，2012.

（责任编辑: 许妍）

A Model of Torpedo Storage Life Test under Temperature Stress

ZHANG Bai-yong1，LIU Kai2，SUN Jiong2，LI Hong-sheng3，LIN Yang1
（1.Department of Weapon Engineering，Naval University of Engineering，Wuhan 430033，China；2.Office of Research and Development，Naval University of Engineering，Wuhan 430033，China；3.Armament Department of the East China Sea Fleet，Ningbo 315121，China）

To estimate torpedo storage life，the main environmental factors influencing torpedo storage life were analyzed and the accelerated life test of a torpedo under temperature stress was conducted.In addition，Arrhenius model was used to estimate the torpedo storage life.Methods for the accelerated life test and for determining parameters of Arrhenius model were presented，and accelerated life tests of the selected main components affecting torpedo storage life were performed to validate these methods.The results show that the research in this paper is efficient for assessing the accelerated life test and estimating the torpedo storage life at room temperature.

torpedo；accelerated life test；temperature stress；Arrhenius model

TJ630；O212

A

1673-1948（2016）03-0222-05

10.11993/j.issn.1673-1948.2016.03.0012

2016-03-22；

2016-04-22.

张百勇（1990-），男，在读硕士，主要研究方向为武器系统运用与保障工程.