航空发动机鲁棒PI控制频域设计

唐钰婷，仇小杰

（中航工业航空动力控制系统研究所，江苏无锡214063）

航空发动机鲁棒PI控制频域设计

唐钰婷，仇小杰

（中航工业航空动力控制系统研究所，江苏无锡214063）

针对航空发动机高、低压转速和压比控制回路，研究中考虑执行机构动态的高阶开环传递函数，根据推广到时滞系统的棱边定理，采用频域方法设计有参数不确定性的非精确模型的鲁棒PI控制器；并利用不确定范围内的发动机非线性模型构成的棱边系统和不确定系统族，验证了鲁棒控制器作用下的系统性能。仿真结果表明，该频域设计方法能使闭环系统的性能指标和鲁棒性均达标。

航空发动机；高阶系统；鲁棒PI控制；频域设计；棱边定理；参数不确定性；时滞系统

1　引言

工程中很难精确描述实际的控制系统，因此所得系统模型常常存在不确定因素。对于航空发动机，建模时的近似、发动机的非线性失真、发动机和执行机构个体间的差异等，都会为系统带来不确定性。此外，发动机性能衰减、元件老化、外部干扰和噪声、环境因素也会为系统带来不确定性。当以上不确定因素对系统造成的影响不可忽略时，就必须将其纳入控制系统设计的考虑范围。而基于有不确定性的非精确模型设计控制器时，鲁棒控制就成为一种重要的解决方法［1-2］。鲁棒控制于1972年首次提出，随后出现了Kharitonov定理［3］、棱边定理、小增益定理、结构奇异值理论、H∞理论［4-5］等理论和方法。

PID控制是国内外现役航空发动机控制系统广泛采用的一种方法［6］，对其结构的研究并未随着时间的推移减弱，而是日益受到重视［7］。PID控制中的一个关键问题是控制参数的整定，控制质量和控制器的鲁棒性都直接受到整定好坏的影响［8］。而通过频域设计整定控制参数，可兼顾对系统响应动态和抑制噪声的要求，具有良好的频域特性，对噪声和干扰的鲁棒性较好。

本文根据推广到时滞系统的棱边定理，研究航空发动机控制系统的鲁棒PI控制频域设计方法，设计有参数不确定性的非精确模型的鲁棒PI控制器。通过PI控制参数的稳定域算法，确定棱边系统的鲁棒PI控制参数集，并利用不确定范围内的发动机非线性模型构成的棱边系统和不确定系统族，验证鲁棒控制器作用下的系统性能。

2　鲁棒PID控制器频域设计

考虑一类时滞系统，可用下述公式描述：

其特征方程可用下述n阶准多项式描述：

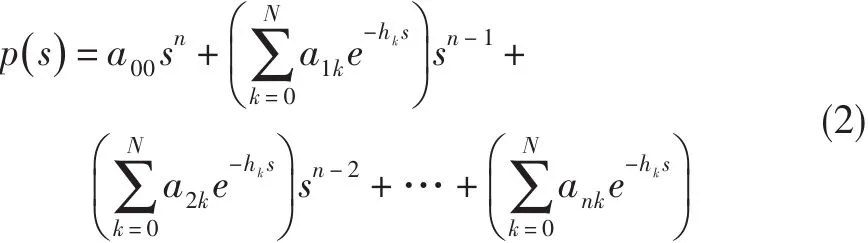
式中：aik=αik+jβik，αik、βik∈R为常数，a00≠0， 0=h0＜h1＜h2＜…＜hN为对应于系统时滞的常量。

定义1［9］假设复平面上有一区域D，当式（2）中的特征准多项式p（ s）的所有零点都在D中时，时滞系统（1）被称为D-稳定的。特别地，如果p（s）为D-稳定的，且D为左半平面，则称p（s）为稳定的。

假设式（2）中p（s）的系数包含不确定因素，则需要关注的就是在考虑了所有可容许的参数摄动的情况下确定D-稳定性。考虑下述一族n阶（实数或复数）准特征多项式：

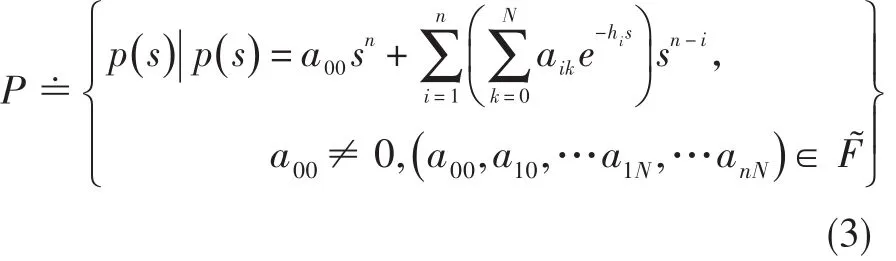
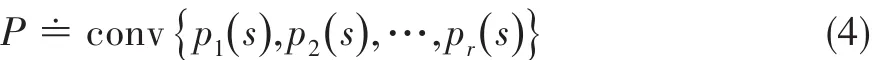
式中：conv表示凸生成。如果P为实数准多项式族，则每个准多项式）的首项系数必须同号［9］。

引理1［9］考虑如式（3）的n阶准多项式多面体P和复平面上的任一区域D满足如下条件：x和y分别为复平面上的两点，存在实数α，对任意一点x∈Dc（Dc为D在复平面的补集）和任意M＞0，若有且 Rey≥α，则可以在Dc内找到一条连续的路径由x通向y。则当且仅当多面体P的所有棱边均是D-稳定时，多面体P才是D-稳定的。

对于式（1）形式的时滞系统，设有有限个数的传递函数

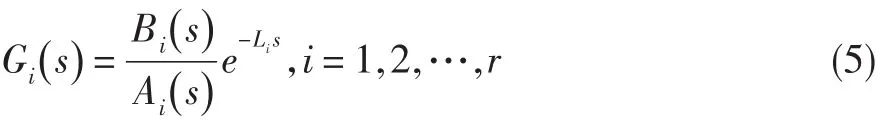
则不确定模型组成的所有凸生成，即不确定时滞系统族为：

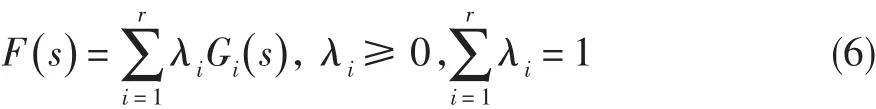
定理1［9］考虑式（6）所示的参数不确定系统族，设计PI控制器进行控制，使该不确定系统族稳定，当且仅当用同一PI控制器使得系统族中每一个）都稳定。

证明［9］考虑有限个数的开环传递函数

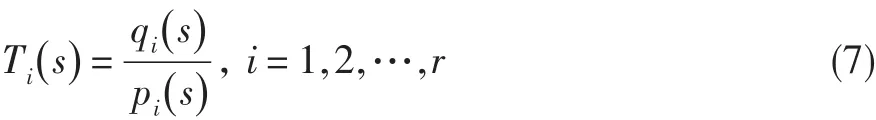
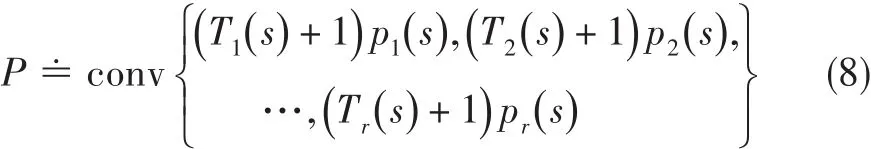
3　发动机转速和压比系统鲁棒控制频域设计

3.1转速系统鲁棒控制频域设计

假设燃油量-转速线性模型的传递函数为包含两个极点一个零点的二阶动态系统，主燃油执行机构的传递函数为带滞后因子的一阶惯性环节，则对于燃油量-转速有：

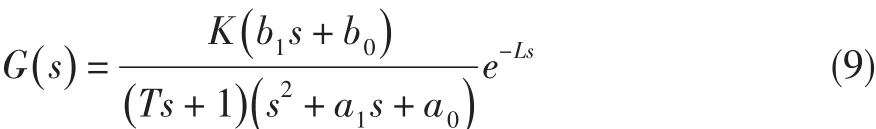
式中：a1、a0、b1、b0为常数，K＞0为执行机构稳态增益，L＞0为执行机构滞后时间，T为执行机构时间常数。为简便快速地验证鲁棒控制频域设计方法的有效性，假设摄动的不确定参数为K和T。根据K和T的摄动范围可得到若干个棱边系统：

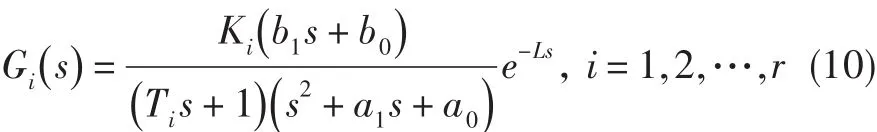
根据文献［10］中PI控制参数的稳定域算法，可得到这若干个棱边系统各自对应的稳定区域。由定理1可知，G（s）稳定的充分必要条件即为这若干个棱边系统同时稳定。换言之所求的PI控制器的稳定区域，即为这若干个棱边系统稳定区域的交集，该交集内的控制器参数均能使系统（9）稳定。在此交集内选择能同时满足系统族各种性能指标的控制参数，即可达到期望的控制要求。

3.2压比系统鲁棒控制频域设计

假设喷口面积-压比线性模型的传递函数为包含两个极点两个零点的二阶动态系统，执行机构的传递函数为带滞后因子的一阶惯性环节，则对于喷口面积-压比有：

式中：b2为常数，其余同式（9）。同样，根据K和T的摄动范围可得到若干个棱边系统：

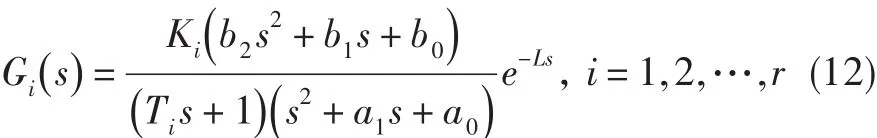
在这若干个棱边系统稳定区域的交集上选择能同时满足系统族各种性能指标的控制参数，即可达到期望的控制要求。

4　仿真算例

以海平面1.0马赫数条件下的转速控制系统为例，发动机中间状态的燃油量-高压转速线性模型为：

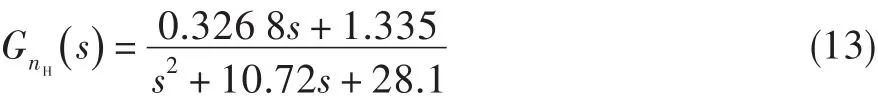
主燃油执行机构的传递函数为：

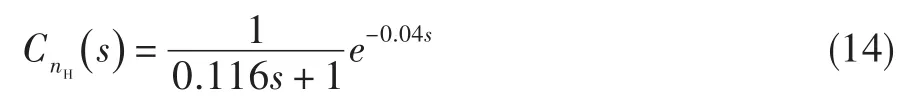
设执行机构的K和T的摄动范围均为±20%，由式（10）可得如下4个棱边系统：

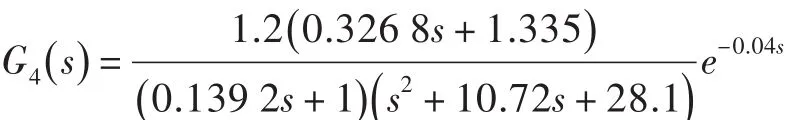
按照文献［10］的方法，分别画出这4个棱边系统所对应的PI控制参数稳定域，见图1。图中阴影部分为稳定域的交集，即目标的参数稳定域。为更快找到合适的控制参数，给棱边系统以一定的幅值裕度和相角裕度要求得到范围更小的目标参数区域，见图2。

图1　棱边系统的控制参数稳定域Fig.1 Control parameter stability region of edge systems

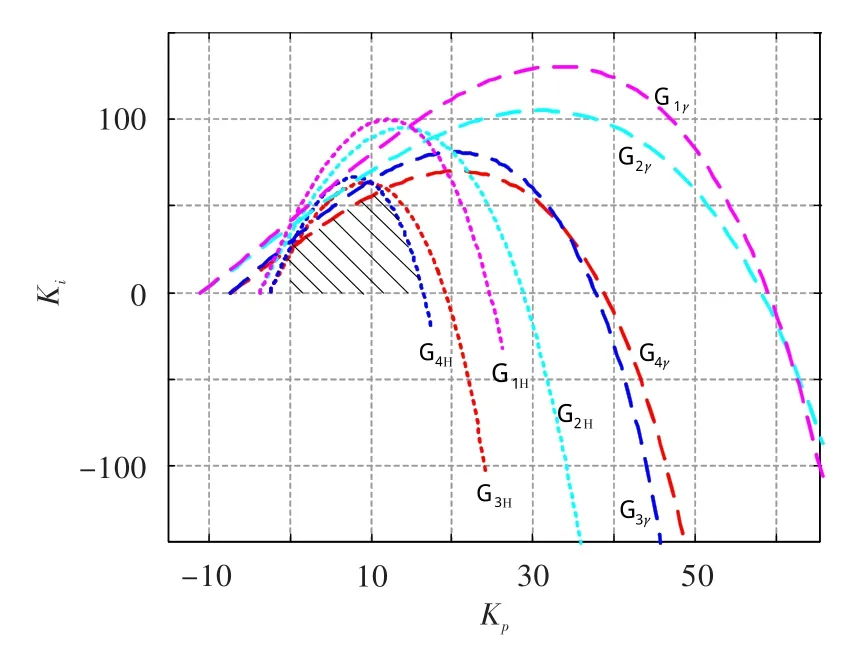
图2　满足幅值裕度和相角裕度的棱边系统稳定域Fig.2 Control parameter stability region satisfied the required stability margin of edge systems

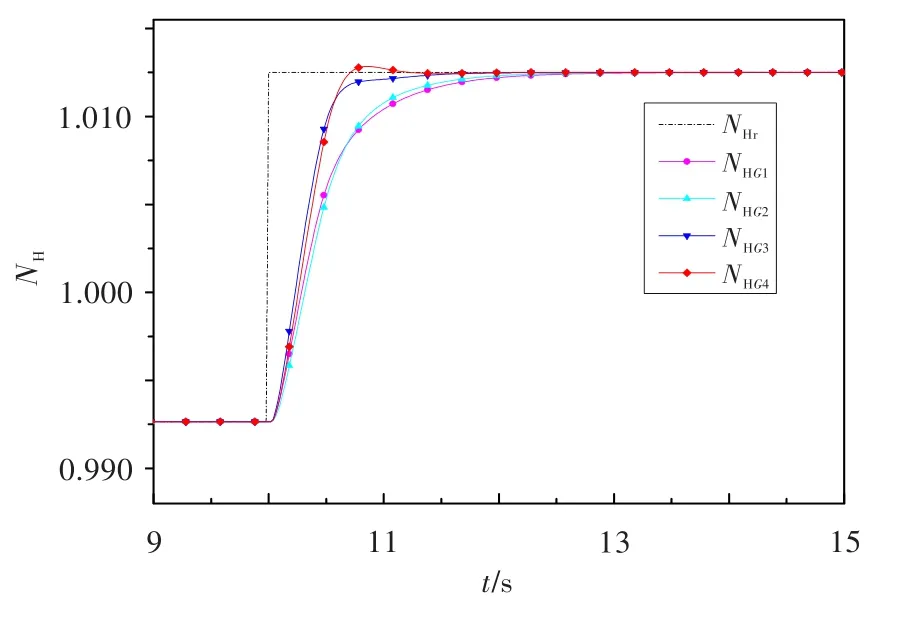
图3　各棱边系统高压转速阶跃响应Fig.3 High pressure rotor speed response of edge systems

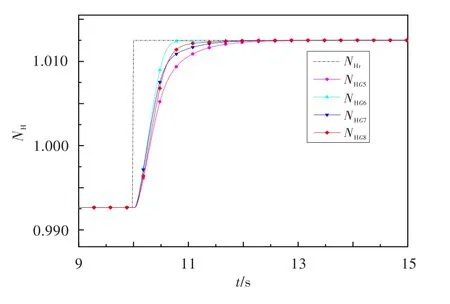
图4　不确定系统族的高压转速阶跃响应Fig.4 High pressure rotor speed response of uncertain system family

同理，可得到该点中间状态燃油量-低压转速的4个棱边系统稳定区域的交集，由此得到鲁棒控制参数，相应的棱边系统和验证系统的仿真结果见图5和图6。图中，NLr为给定低压转速，NLG1～NLG4分别为燃油量-低压转速4个棱边系统的低压转速响应，NLG5～NLG8分别为燃油量-低压转速4个验证系统的低压转速响应。由图5可知，各系统均能达到稳定，响应中超调量最大的是G4（）s，不超过1.975%；调节时间最长的是G1（）s，不超过1.48 s，能满足期望的性能要求。由图6可看出，4个验证系统均达到了稳定的超调量最大为0.400%，的调节时间最长为1.40 s，控制效果较好。

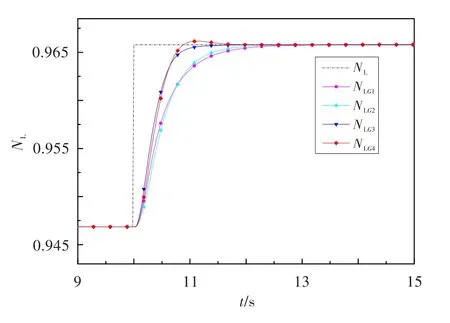
图5　各棱边系统低压转速阶跃响应Fig.5 Low pressure rotor speed response of edge systems

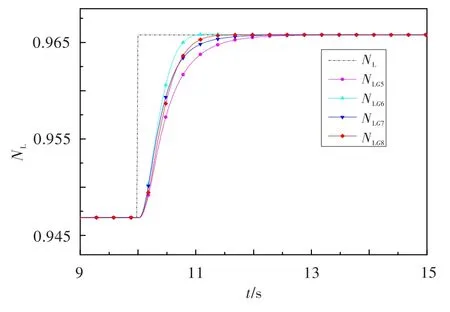
图6　不确定系统族的低压转速阶跃响应Fig.6 Low pressure rotor speed response of uncertain system family

以海平面1.0马赫数条件下的压比控制系统为例，发动机中间状态的喷口面积-压比线性模型为：

执行机构的传递函数采用以下形式：

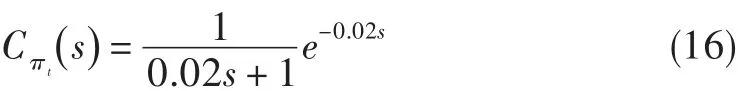
设执行机构的K和T的摄动范围均为±20%，采用类似于上述的方法，分别画出4个棱边系统所对应的PI控制参数稳定区域，并给以一定的幅值裕度和相角裕度要求，得到稳定区域的交集。选择鲁棒控制参数相应的棱边系统和验证系统的仿真结果见图7和图8。图中，πtr为给定压比，πtG1～πtG4分别为喷口面积-压比4个棱边系统的压比响应，πtG5～πtG8分别为喷口面积-压比4个验证系统的压比响应。由图7可知，各系统均能达到稳定，响应均无超调；调节时间最长的是G1（）s，不超过0.400 s，能满足期望的性能要求。从图8可看出，4个验证系统均达到了稳定，响应均无超调，G5（）s的调节时间最长为0.400 s，控制效果良好。

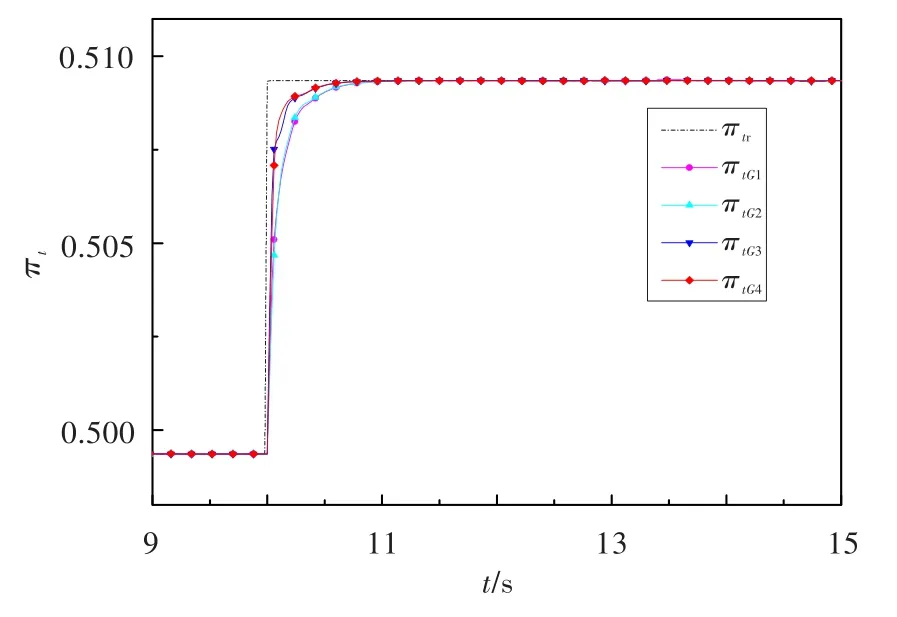
图7　各棱边系统压比阶跃响应Fig.7 Pressure ratio response of edge systems

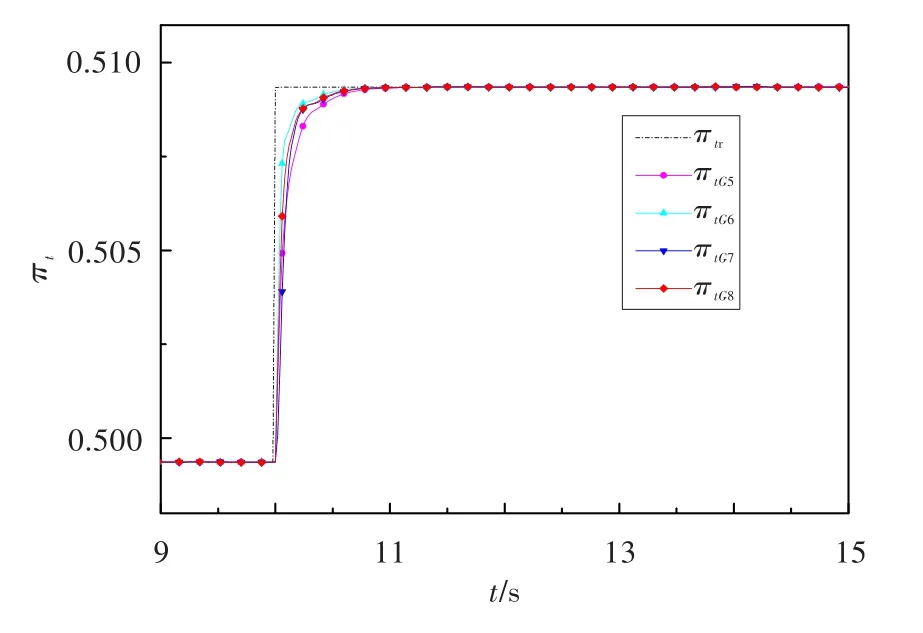
图8　不确定系统族的压比阶跃响应Fig.8 Pressure ratio response of uncertain system family

5　结束语

本文将实际的航空发动机控制中将出现不确定因素的问题纳入考虑，针对发动机转速控制系统和压比控制系统，利用频域方法设计基于有不确定性的非精确模型的鲁棒控制器。根据推广到时滞系统的棱边定理，一个高维准多项式多面体的稳定性问题可转化成若干个多面体棱边系统的稳定性问题，求得这些棱边系统的稳定域交集即可得到不确定系统族的控制参数取值范围。并以具体工作点的转速和压比作为被控对象，给系统参数以一定的变化，在稳定域的交集上选择能使控制系统达到性能指标的鲁棒控制参数，利用在不确定范围里的系统验证了鲁棒控制器作用下的系统性能。非线性模型仿真结果表明，该频域设计方法得到的鲁棒控制参数的控制效果较好，扩大了航空发动机控制系统频域设计的适用范围，具有较好的应用前景。

［1］ Silva G J，Datta A，Bhattacharyya S P.On the stability and controller robustness of some popular PID tuning rules［J］. IEEE Trans.on Automatic Control，2003，48（9）：1638—1641.

［2］ Silva G J，Datta A，Bhattacharyya S P.Robust control de⁃sign using the PID controller［C］//.Proc.of the 41st IEEE Conf.on Decision and Control.2002.

［3］ Kharitonov V L.Asymptotic stability of an equilibrium po⁃sition of a family of systems of linear differential equations ［J］.Differential Uravnen.，1978，14：2086—2088.

［4］ Kimura H.Robust stability for a class of transfer functions ［J］.IEEE Trans.on Automatic Control，1984，29（9）：788—793.

［5］ Doyle J，Glover K，Khargonekar P，et al.State space solu⁃tion to standardH2andH∞control problem［J］.IEEE Trans.on Automatic Control，1989，34（8）：831—847.

［6］ 孙健国.面向21世纪航空动力控制展望［J］.航空动力学报，2001，16（2）：97—102.

［7］ Isaksson A，Hagglund T.Editorial PID control［J］.IEE. Proc.Control Theory Appl.，2002，149（1）：1—2.

［8］ Wang Q G，Lee T H，Fung H W，et al.PID tuning for im⁃proved performance［J］.IEEE Transactions on Control Sys⁃tem Technology，1999，7（4）：457—465.

［9］ Minyue F，Andrzej W O，Michael P P.Robust stability for time-delay systems：the edge theorem and graphical tests ［J］.IEEE Trans.on Automatic Control，1989，34（8）：813—820.

［10］唐钰婷，黄金泉，潘慕绚.基于幅相裕度频域法PI参数最优整定方法［C］//.中国航空学会第十六届航空发动机自动控制专业学术会议论文集.2012.

Frequency domain design of robust PI control for aero-engine

TANG Yu-ting，QIU Xiao-jie

（AVIC Aviation Motor Control System Institute，Wuxi 214063，China）

For the aero-engine high and low pressure rotor speed control loops and pressure ratio control loop，considering dynamic high order open loop transfer function of execute mechanism，the frequency do⁃main method of designing the robust PI controller for the non-exact models with parameter uncertainties was researched，which based on the edge theorem extended to time-delay systems；then the edge systems and the uncertain system family contained the engine nonlinear model that in the range of uncertainty were used to validate the system performance under the robust controller.Simulation results demonstrate that the design method satisfies performance indices and robustness of closed loop system.

aero-engine；high order system；robust PI control；frequency domain design；edge theorem；parametric uncertainty；time-delay system

V233.7+3

A

1672-2620（2016）04-0038-05

2016-05-30；

2016-08-13

唐钰婷（1988-），女，河南滑县人，助理工程师，硕士，从事航空发动机控制研究。