偏心比对S形流道雷达散射特性的影响

李岳锋，廖华琳，卿太木，杨青真，母鸿瑞，邓雪娇

（1.中国涡轮燃气研究院，成都610500；2.西北工业大学动力与能源学院，西安710072）

偏心比对S形流道雷达散射特性的影响

李岳锋1，廖华琳1，卿太木1，杨青真2，母鸿瑞1，邓雪娇1

（1.中国涡轮燃气研究院，成都610500；2.西北工业大学动力与能源学院，西安710072）

在进/出口形状、进/出口面积、中心线变化规律、面积变化规律等设计参数不变的条件下，采用超椭圆方法设计了11种不同偏心比的S形流道。同时，借助迭代物理光学法与等效边缘电磁流绕射方法，对不同偏心比的S形流道进行了雷达散射特性的数值仿真分析。结果表明：若将不同偏心比S形流道的雷达散射截面变化曲线看作是波的传播轨迹，相对于偏心比为0的流道，偏心比改变了波的相位、振幅；偏心比越大，其相位越滞后、振幅越小。

偏心比；迭代物理光学法；等效边缘电磁流法；单端开口腔体；散射；绕射；雷达散射截面；隐身技术

1　引言

单端开口腔体结构是雷达目标的一类特殊结构，通常会在一个较宽的频段内对目标的雷达散射截面（RCS）产生很大贡献。入射雷达波进入单端开口腔体后，经过腔体表面的直接反射、多次反射和口径边缘绕射，反射波沿入射方向返回被雷达直接接收，形成单站雷达主要的发现/锁定信号。进气道和喷管是飞机上的典型单端开口腔体结构，是飞机前向和后向主要的雷达散射源。其腔体结构的特征尺寸与入射电磁波波长相差较大，在电磁学上属于电大尺寸结构。同时，腔体结构内部存在电磁波的多次反射，使得其电磁散射求解成为电磁学上的难点与热点。国内外学者针对电大尺寸腔体结构的数值仿真算法进行了充分的研究，以高频算法和高低频耦合算法为主，包括弹跳射线法［1］、导波模式法［2］、迭代物理光学法［3］及高低频耦合算法［4-6］等。其中，迭代物理光学法因其精度高、占用内存小等优点，在电大尺寸腔体结构的数值仿真中应用较多。

目前，针对军用飞机腔体强散射的抑制措施主要有如下几种：①将进排气系统设计成背负式，利用机身对腔体结构进行遮挡，如美国的“全球鹰”隐身无人侦察机；②在进排气系统进出口截面处采用网状格栅，对入射和反射雷达波进行过滤，如美国的F-117及RQ-170无人机；③将进排气系统流道设计成S形，以增加电磁波在流道内部的反射次数，改变反射波方向，减弱反射波能量，如美国的F-117、B-2、F-22、F-35、X-47B等。现役隐身飞机有时也将①和③或②和③措施组合使用，如“全球鹰”采用的是①和③组合，而F-117、RQ-170采用②和③组合。由上述典型隐身飞机的组合隐身措施可知，将腔体结构设计成S形是减小其雷达散射截面最有效的办法之一。国内外针对S形流道电磁散射特性的研究较多，但详细分析不同偏心比对S形流道电磁散射特性的研究较少［7-8］。

通过对F-117、F-22、F-35及J-20等隐身飞机布局的分析可知，其进气道均采用平行四边形或类菱形进口，由此可推断平行四边形或类菱形进出口流道是隐身飞机的较好选择。基于上述分析，本文采用超椭圆方法设计了11种上下弯折、偏心比不同的菱形S形流道，并对这11种S形流道的电磁散射特性进行了数值仿真研究，研究结果可为此类S形流道的雷达隐身设计提供参考。

2　物理模型

在进口/出口形状、进口/出口面积、面积变化规律、中心线变化规律等设计参数不变的条件下，采用超椭圆方法［9］设计了11种不同偏心比的菱形S形流道，其中S形流道中心线选择前急后缓、面积变化选择缓急相当的变化规律［10］。偏心比D/L的变化范围为0～10/24，变化因子为1/24。图1示出了偏心比为5/24的菱形S形流道，图中D为S形流道进出口截面中心点在垂直方向的距离，L为S形流道在水平方向的长度，其菱形对角线比A/B为1.75。

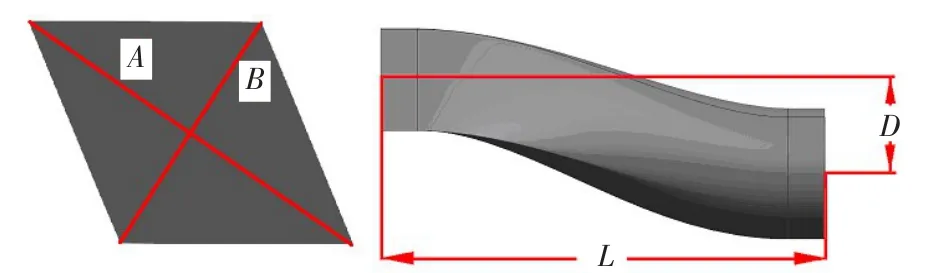
图1　偏心比为5/24的菱形S形流道Fig.1 Diamond S-shaped inlet/nozzle with eccentricity ratio 5/24

3　数值方法

主要采用等效边缘电磁流方法（EEC）［11］模拟S形流道口径边缘绕射场的RCS，采用迭代物理光学法（IPO）［12］模拟S形流道腔体内部散射场的RCS。由于迭代物理光学法基于物理光学近似，只有能相互照射的面元之间才能产生等效电磁流，因此在采用IPO方法计算等效电磁流之前，需要对腔体内部壁面面元进行遮挡关系判断。本文采用文献［13］提出的射线追踪方法提高遮挡关系的判断效率，进而提高迭代物理光学法的计算效率。

因迭代物理光学法是高频算法，在目标特征尺寸远大于入射波波长时目标散射场的计算才有效。鉴于此，本文将研究的S流道终端处的旋转部件假设为平面，以保证S形流道内部散射场计算的准确性。其求解S形流道RCS的步骤如下：①根据入射场与电磁场等效原理，求得S形流道口径面的等效电磁场；②根据S形流道口径面上的等效电磁场，由Kirchhoff公式求得S形流道壁面上的初始磁场；③判断S形喷管壁面各个面元之间的遮挡/照射关系；④根据遮挡/照射关系与磁场积分方程，迭代求得壁面各个面元的真实电磁流分布；⑤根据壁面的真实电磁流分布与Kirchhoff公式，求得S形流道口径面上的电磁场分布；⑥根据等效原理，求得S形流道的反射电磁场；⑦根据入射电场与反射电场，求得S形喷管的RCS。

4　结果与分析

本文计算的入射波频率 f=6 GHz，S形流道壁面采用三角形网格进行划分，网格总数约为4万。

4.1水平极化方式

图2是水平极化方式下不同偏心比S形流道边缘绕射场的RCS随探测角的变化规律。因边缘绕射场只与流道的进出口形状有关，而本文分析的11 种S形流道均为菱形过渡到圆的流道，所以不同偏心比S形流道边缘绕射场的RCS变化规律保持一致。由图2可知，在0°探测角时，S形流道边缘绕射场的RCS最大。这主要是因为0°探测角时的入射电磁波与流道边缘切向垂直，此时在边缘任意点处产生的绕射场是以平面传播的形式向四周散射，而本文计算的是单站雷达时的电磁特性，因此绕射场定有一条绕射波沿入射方向返回被雷达直接接收，导致0°探测角处的绕射场RCS最大。在0°～7°探测角范围内，边缘绕射场的RCS呈快速下降趋势。这主要是因为随着探测角度的偏大，在0°探测角形成的平面绕射场转换成锥面绕射波，此时形成的绕射波与入射反向形成一定夹角，使得沿入射方向返回的绕射波急剧减少。在7°～40°探测角范围内，边缘绕射场的RCS呈波状变化，其波峰值呈缓慢增长趋势，这与入射电场的极化方式密切相关。水平极化方式下边缘绕射场的RCS在小探测角时会大幅度降低，在大探测角时呈缓慢升高趋势。

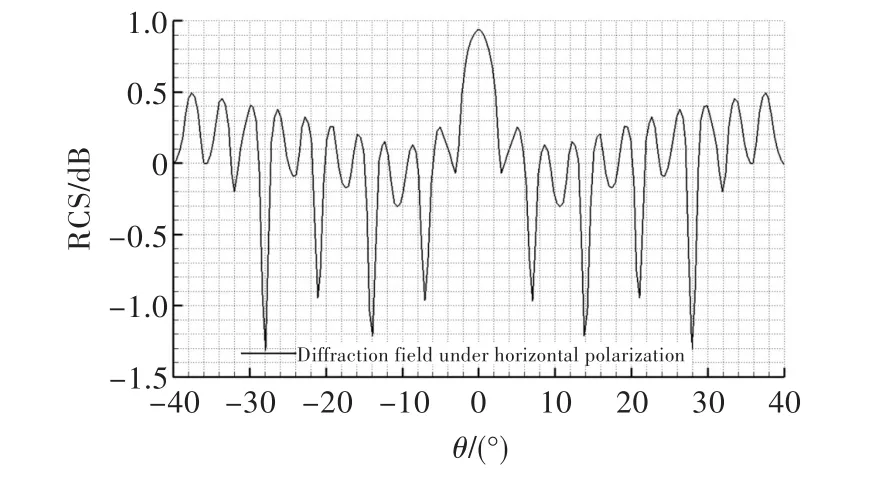
图2水平极化方式下边缘绕射场的RCSFig.2 The RCS of diffraction under horizontal polarization

图3是水平极化方式下11种不同偏心比S形流道腔体内部散射场的RCS随探测角的变化规律。可见，模型A处于0°探测角时其散射场的RCS最大，这主要是因为在0°探测角时入射电磁波直射在假设的流道终端面上形成强反射导致。因为模型A的偏心比为0，因此其散射场的RCS关于0°探测角对称。随着探测角的增大，模型A散射场的RCS呈有波动的降低趋势。这主要是因为随着探测角的增大，入射波对流道假设终端面的直接照射变为对流道下侧壁面的斜照射，而呈波动变化主要是与入射电磁波在空间呈波状传播有直接关系。

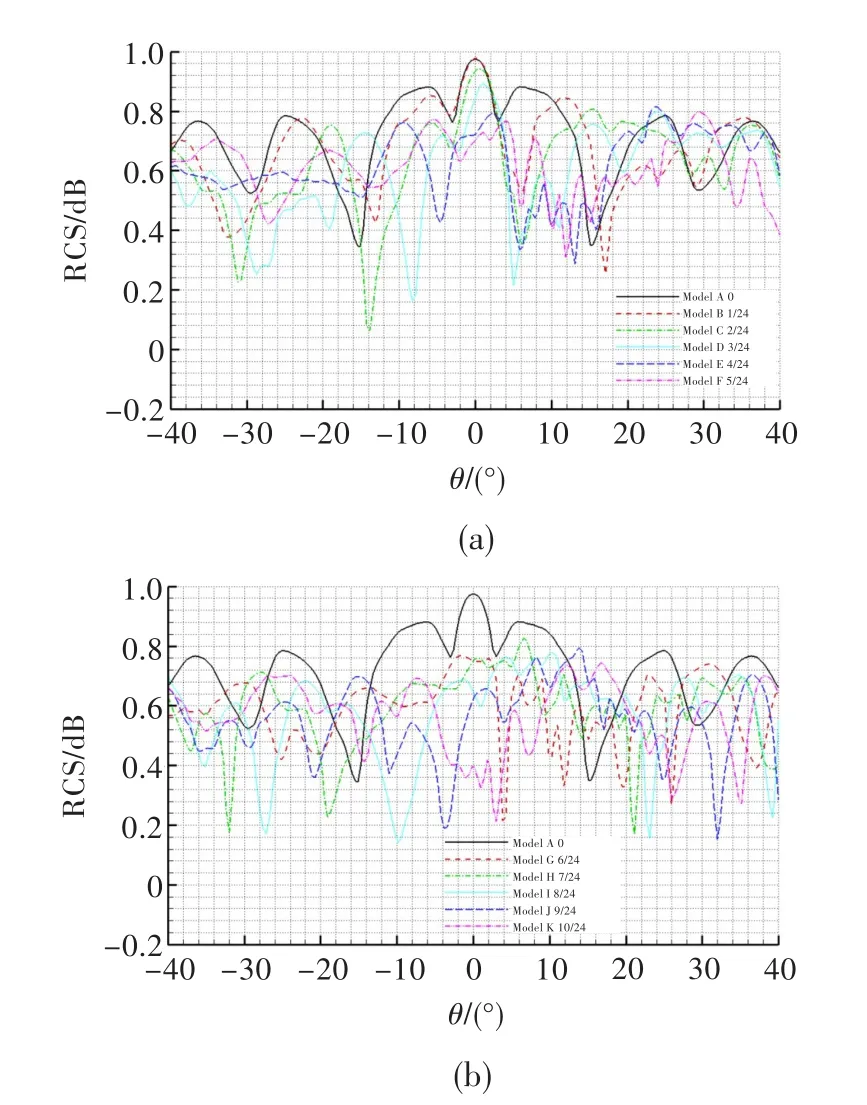
图3　水平极化方式下内腔散射场的RCSFig.3 The RCS of scattering under horizontal polarization

对比这11种模型发现，随着偏心比的增大，S形流道散射场的RCS最大值偏离0°移向正探测角，且偏心比越大偏离的角度越大；带有偏心比的10种S形流道散射场的RCS值不再关于0°探测角对称，且偏心比越大正探测角与负探测角范围内的RCS值差异越大。造成最大值偏离的主要原因，是偏心比增大使得0°探测角时S形流道第一个拐弯处对其终端面的遮挡增大，此时入射电磁波只能部分或完全不能照射在S形流道终端的假设面上。上述分析既可说明S形流道最大值偏离0°探测角的原因，又可说明其最大值降低的原因。

值得注意的是，当偏心比增大至6/24（模型G）与7/24（模型H）时，0°附近的RCS不再随偏心比的增大而降低，而是略有升高，但其散射场的RCS还是远低于偏心比为0的流道。偏心比为7/24时偏离0°探测角的最大值也较其他S形流道有所提高。

分析模型A和模型B的RCS变化规律可知，若将模型A的变化规律视为波的传播路径，模型B相比模型A来说则是相位滞后、振幅降低的波的传播路径。推及到其余几种S形流道中可以发现，偏心比越大，波的相位越滞后，其振幅越小。

综合上述分析可知，S形流道相对直流道来说，其散射场的RCS有所降低，特别是偏心比越大，RCS降幅越大。其在-10°～10°探测角范围内散射场的RCS远小于直流道，这表明S形流道是降低腔体结构RCS有效的手段之一。

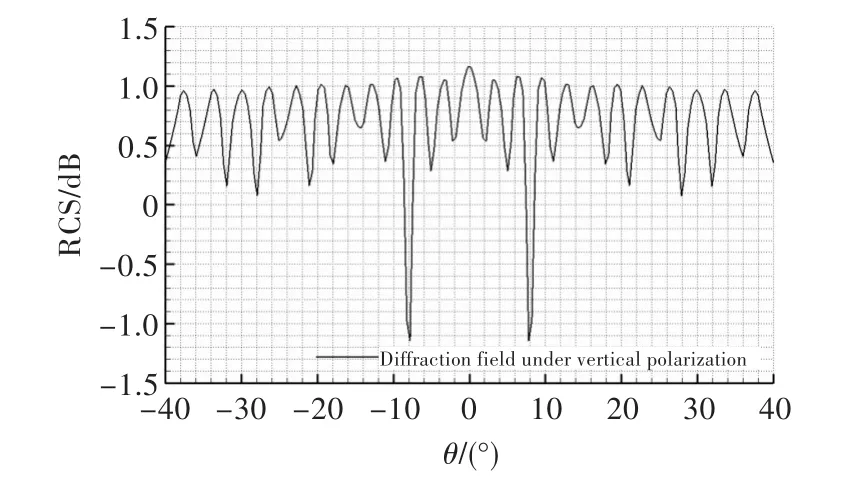
图4　垂直极化方式下边缘绕射场的RCSFig.4 The RCS of diffraction under vertical polarization

4.2垂直极化方式

图4是垂直极化方式下不同偏心比S形流道边缘绕射场的RCS随探测角的变化规律。与水平极化方式类似，在0°探测角处，S形流道边缘绕射场的RCS最大。全局探测范围内，垂直极化方式下绕射场的RCS均高于水平极化。0°～40°探测角范围内，随着探测角的增大，绕射场的RCS呈波状变化，且波峰值缓慢降低、降幅较小，与水平极化方式下绕射场RCS先急速下降后缓慢升高的变化趋势不同。

图5是垂直极化方式下11种不同偏心比S形流道腔体内部散射场的RCS随探测角的变化规律。垂直极化与水平极化方式下散射场的RCS变化趋势较为类似，但也有不同之处。相同之处在于模型G和模型H在0°探测角处的RCS有所回升，都可将11种流道散射场的RCS变化规律认为是不同相位与振幅的波传播路径。不同之处在于模型A散射场的RCS变化趋势有所不同，模型B～模型F在0°～10°探测角区间内散射场的RCS降低幅度较大。

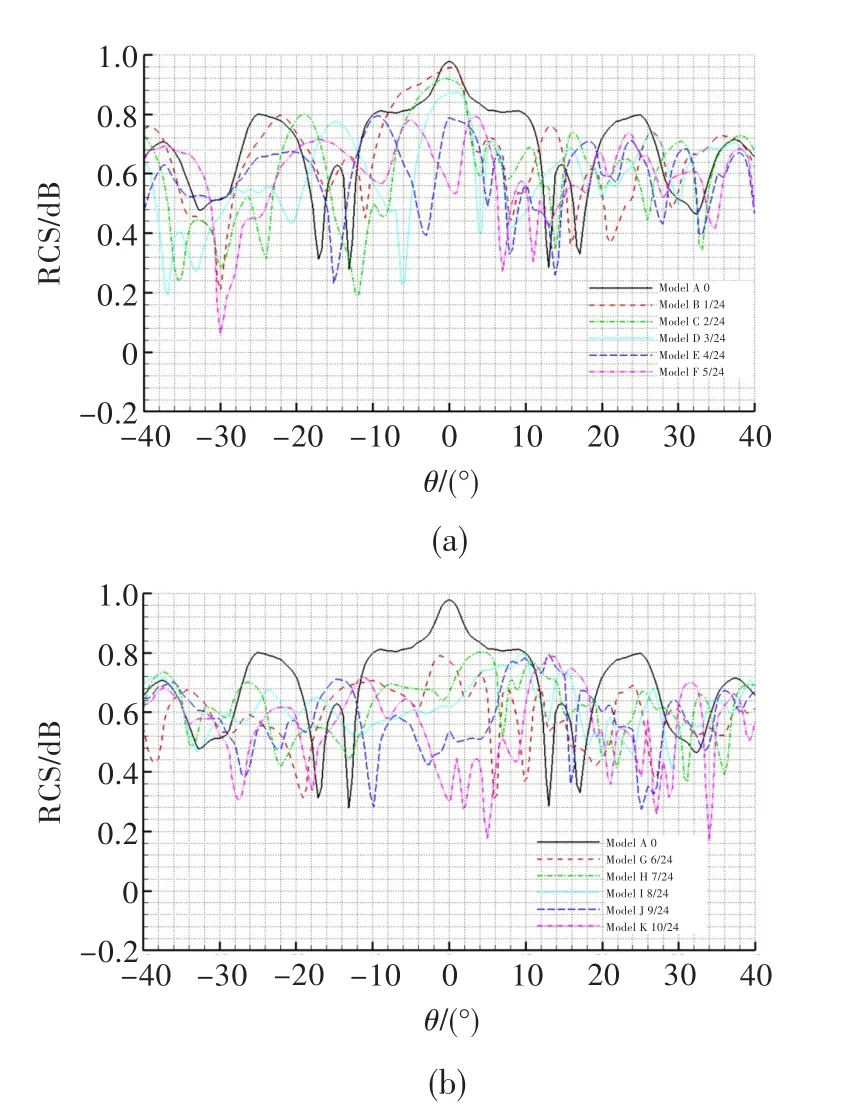
图5　垂直极化方式下内腔散射场的RCSFig.5 The RCS of scattering under vertical polarization

5　结论

（1）偏心比对S形流道边缘绕射场的RCS无任何影响。

（2）在-10°～10°探测角范围内，偏心比可有效减小流道散射场的RCS，且随着偏心比的增大其效果越明显；在-20°～20°探测范围内，偏心比为5/24的S形流道较其他流道有更低的RCS。

（3）若将不同偏心比的RCS变化曲线看作是波的传播路径，相对于直流道，偏心比改变了波的相位、振幅，且偏心比越大，其相位越滞后、振幅越小。

［1］ Pathak P H，Burkholder R J.Model，ray and beam tech⁃niques for analyzing the EM scattering by open-ended waveguide cavities［J］.IEEE Transactions on Antennas and Propagation，1989，37（5）：101—109.

［2］ Johason T W，Moffat D L.Electromagnetic scattering by open circular wave guides［J］.Radio Science，1982，17：1547—1556.

［3］ Robert J B，Tomas L.Forward-backward iterative physical optics algorithm for computing the RCS of open ended cav⁃ities［J］.IEEE Transactions on Antennas and Propagation，2005，53（2）：793—799.

［4］ Lee R，Chia T T.Analysis of electromagnetic scattering from a cavity with a complex termination by means of a hy⁃brid ray-FDTD method［J］.IEEE Transactions on Anten⁃nas and Propagation，1993，41（11）：1560—1569.

［5］ 何小祥，徐金平.改进的IPO与FEM混合法分析复杂电大腔体电磁散射［J］.电波科学学报，2004，19（5）：607—612.

［6］ 罗威.三维电大复杂腔体电磁散射问题的混合快速算法研究［D］.西安：西安电子科技大学，2007.

［7］ 郭文彦，朱颜镇，李海涛.飞机进气道的高频电磁散射特性及RCS计算［J］.哈尔滨工业大学学报，1999，31（1）：123—129.

［8］ 姬金祖，武哲，刘战合.S弯进气道隐身设计中弯度参数研究［J］.西安电子科技大学学报，2009，36（4）：746—750.

［9］ 李岳锋，杨青真，孙志强.超椭圆S形进气道的设计及气动性能研究［J］.计算机仿真，2011，28（3）：82—85.

［10］Lee C C，Boekicker C.Subsonic diffuser design and perfor⁃mance for advance fighter aircraft［R］.AIAA 85-3073，1985.

［11］聂在平，方大纲.目标与环境电磁散射特性建模-理论，方法与实现（基础篇）［M］.北京：国防工业出版社，2009：210—211.

［12］Basteriro F，Rodriguez J L，Burkholder R J.An iterative physical optics approach for analyzing the electromagnetic scattering by large open-ended cavities［J］.IEEE Transac⁃tions on Antennas and Propagation，1995，43（4）：356—361.

［13］陈立海，杨青真，陈玲玲，等.不同喷口修型的二元收敛喷管RCS数值模拟［J］.航空动力学报，2012，27（3）：513—520.

Investigation on radar cross-section of S-shaped channel with different eccentric ratio

LI Yue-feng1，LIAO Hua-lin1，QING Tai-mu1，YANG Qing-zhen2，MU Hong-rui1，DENG Xue-jiao1

（1.China Gas Turbine Establishment，Chengdu 610500，China；2.School of Power and Energy，Northwestern Polytechnical University，Xi'an 710072，China）

Under the conditions where the shape and area of intake and outlet，the area variation and the center-line variation are constant，11 S-shaped diamond inlets/nozzles with different eccentricity-ratio were designed by the super-ellipse method.The radar cross-section（RCS）of the scattering filed were analyzed with iterative physical optic approach and equivalent edge currents method.The results show that if the change curve of the RCS of channel with different eccentricity is considered as the wave trajectory，com⁃pared with the channel with the eccentricity-ratio 0，the eccentricity-ratio changes the phase and amplitude of the wave.And the larger the eccentricity-ratio is，the phase lags more and the amplitude gets smaller.

eccentricityratio；iterativephysicalopticapproach（IPO）；equivalentedgecurrentsmethod（EEC）；open-ended cavity；scattering；diffraction；radar cross-section（RCS）；stealthtechnology

V228.7；V211

A

1672-2620（2016）04-0013-04

2016-06-27；

2016-08-11

李岳锋（1984-），男，陕西富平人，博士，工程师，主要从事进排气系统气动、红外及雷达隐身研究工作。