紧凑喷射下钝体回流区内当量比影响因素数值研究

曹宗华，谢建光，李　锋，林建府

（中国燃气涡轮研究院，成都610500）

紧凑喷射下钝体回流区内当量比影响因素数值研究

曹宗华，谢建光，李锋，林建府

（中国燃气涡轮研究院，成都610500）

针对先进加力燃烧室火焰稳定器采用的紧凑喷射模式，以包含一个钝体稳定器的矩形模型件为研究对象，数值研究了加力条件下来流温度和速度以及喷口直径、喷射距离、钝体宽度对钝体稳定器后回流区局部当量比的影响。结果表明：提高来流温度、速度，扩大喷口直径，增加喷射距离或槽宽，都会增大钝体回流区内的当量比。最后，利用获得的数据建立了简单拟合函数，以预估紧凑喷射模式下回流区内的局部当量比。

航空发动机；加力燃烧室；火焰稳定器；紧凑喷射；局部当量比；数值计算

1　引言

新一代高推重比航空发动机加力燃烧室的进口温度极高，且有继续增高的趋势，这将导致加力燃烧室中燃油自燃时间缩短。研究表明，当温度高于1 300 K时，燃油自燃时间将小于1 ms［1］。如采用现有燃油喷射方式，燃油在达到稳定器前就会发生自燃，导致稳定器烧毁。通过减小燃油喷射点到火焰稳定器的距离，可以有效避免燃油在稳定器前发生自燃。为此，先进加力燃烧室采用了火焰稳定器与喷油杆的一体化设计［2］，该设计下燃油的喷射模式称为紧凑喷射（CCI）。

国外就紧凑喷射模式开展了深入研究。Lovett等［3］的研究表明，基于传统加力预混喷射的经典火焰稳定理论［4］不完全适用于紧凑喷射模式。紧凑喷射模式导致火焰区的燃油分布具有不均匀性，其火焰稳定性除预混模式下的影响因素——钝体尾缘气流速度、钝体直径、压力和温度外，还取决于回流区内局部当量比。Klusmeyer［5］采用光谱照相技术，研究了紧凑喷射模式下，喷口直径、全局当量比对钝体回流区内局部当量比的影响，给出了回流区内当量比随全局当量比、喷口直径和动量比变化的拟合方程。

国内在此领域的研究还处于起步阶段，未见相关文献发表。本文以先进加力燃烧室采用的火焰稳定器与喷油杆一体化设计为背景，以影响钝体火焰稳定关键要素——回流区内当量比为对象，数值研究燃油紧凑喷射下火焰稳定器后方的燃油分布，以及横向气流速度、温度、喷口直径、喷射位置、钝体宽度等对回流区内当量比的影响。

2　模型简介及计算方法

2.1模型简介

以文献［5］的实验装置为基础构建了计算模型，见图1。模型结构尺寸为宽度（W）76.2 mm，高度（H）152.4 mm。流路中，设置了一个前部流线外形，后端截面的钝体稳定器横跨在矩形流道内，高度为76.2 mm，宽度为W1。在距离钝体稳定器尾缘距离为L的上游，稳定器的上下两侧各设置3个燃油喷口，喷口直径为d。

假定模型的来流为污染空气，且速度和温度可变，使钝体稳定器尾缘的气流速度和温度与加力环境下相当。研究的速度范围180～250 m/s，温度范围1 050～1 300 K。

上述模型的边界设置，涵盖了新一代加力燃烧室的工作范围，可满足加力条件下横向气流速度、温度、喷口直径、喷射位置、钝体宽度等对钝体回流区内当量比影响趋势的研究。

图1　钝体火焰稳定器简图Fig.1 Sketch of the bluff body flame holder

2.2计算方法

利用ICEM软件对模型进行六面体网格划分，钝体区域采用较细的网格，见图2。

运用FLUENT 14.5，采用有限体积法求解三维流场。湍流模型采用Realizablek-ε模型，近壁采用标准壁面函数，空间离散采用二阶迎风格式，压力与速度间采用耦合运算法则。

图2　钝体火焰稳定器计算网格Fig.2 Computational grid domain of the bluff body flame holder

本模型中，燃油经过直射喷嘴被雾化成燃油液珠，在气体中经历随动和蒸发等复杂过程。燃油的雾化过程采用FLUENT自带的plain-orifice-atomizer喷嘴模型，其雾化锥角、液滴直径分别由式（1）、式（2）计算。

式中：s为分布指数，取3.5；d32为索太尔平均直径；λ=d/8；We≡ρlu2λ/σ，σ为液滴表面张力，u为喷射速度。

油滴离开喷嘴后的运动轨迹受气相影响，运动方程见公式（4）：

式中：up为燃油粒子速度，ug为气流速度，μg为气体粘性系数，CD为作用力系数，dp为燃油粒子直径，t为时间。

边界条件给定为：气流进口为速度进口，出口为环境压力出口，固体壁面无滑移边界。由于气流速度较高，故流体采用理想气体模型。

为验证数值计算方法的有效性，依据文献［5］，环境设定为：来流温度1 173 K，钝体稳定器后端面尾缘速度219 m/s，喷口直径0.61 mm。数值模拟不同燃油流量下钝体回流区内的局部当量比，模拟结果与测量值的对比如图3所示。图中，Φa为总当量比，Φl为回流区的局部当量比。可见：回流区内的局部当量比的数值模拟结果与试验结果趋势一致，与文献［5］的试验结果吻合较好。局部当量比随总当量比的增加先增加，在总当量比0.4时达到最大，然后随总当量比的增加逐渐降低。

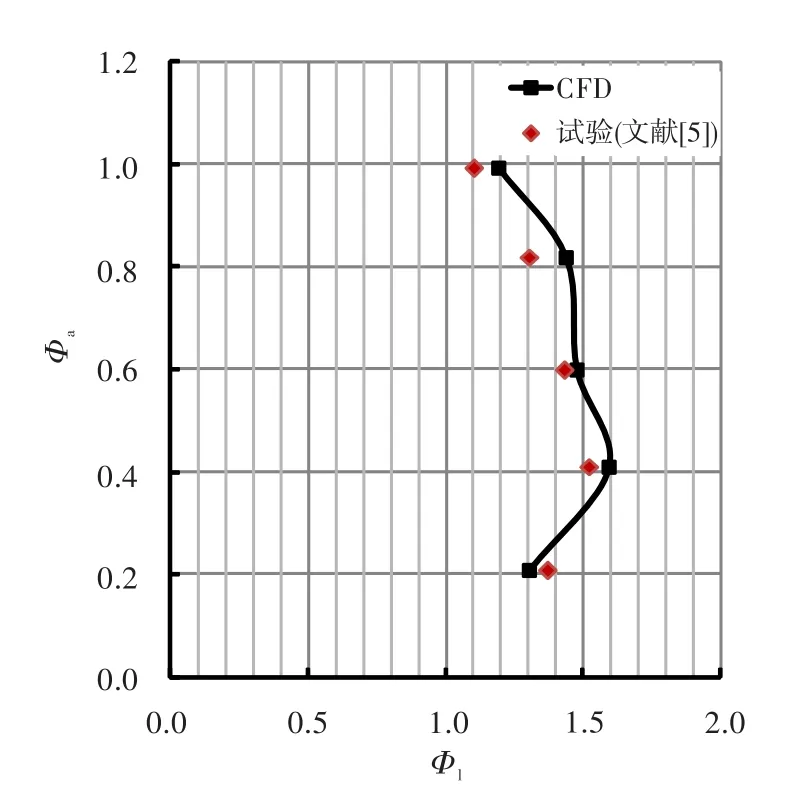
图3　CFD结果和试验数据比较Fig.3 Comparison between the CFD computation and experimental data

3　回流区内当量比影响因素分析

依据加力燃烧室工作环境，并考虑紧凑喷射钝体的关键几何特征，制定了表1的模拟分析范围。

表1　计算工况Table 1 Computed parameters

（1）喷口直径

图4示出了喷射距离、来流温度和速度一定时，喷口直径改变对钝体回流区内当量比的影响。可见：总当量比一定的情况下，回流区内局部当量比随喷口直径的增加而增加。这是因为燃油流量一定时，随着喷口直径的增大，燃油喷射速度变小，油气动量比减小，穿透深度降低，导致靠近稳定器壁面附近的燃油浓度高（图5，图中阴影部分表示钝体稳定器尾缘轮廓），进入钝体回流区内的燃油量增多，提高了回流区内的局部当量比。

图4　不同喷口直径下的回流区当量比Fig.4 Comparison ofΦlwith various injectors

图5　钝体尾缘近壁面附近燃油分布曲线Fig.5 Kerosene distributions with various injectors near the bluff body wall

（2）喷射距离

图6示出了喷口直径为0.61 mm、来流温度和速度保持不变时，距离钝体稳定器尾缘距离为L的上游供油对钝体回流区内当量比的影响。由图可知：当总当量比较大、L为50.0 mm和65.0 mm时，两者回流区内的当量比较为接近，且明显比L为25.4 mm的高。原因在于：在本文的研究范围内，随着L的增加，燃油的蒸发度也随之增加；但当距离大于一定值时，燃油已接近完全蒸发（图7）。燃油的蒸发量直接影响了进入钝体回流区内的燃油量，所以回流区内的局部当量先随喷射距离的增加而增加，当L大于一定值时钝体回流区内的局部当量比很接近。

图6　燃油喷射离钝体稳定器尾缘不同距离下的回流区当量比（d=0.61 mm）Fig.6 Comparison ofΦlwith different distance from the trailing edge（d=0.61 mm）

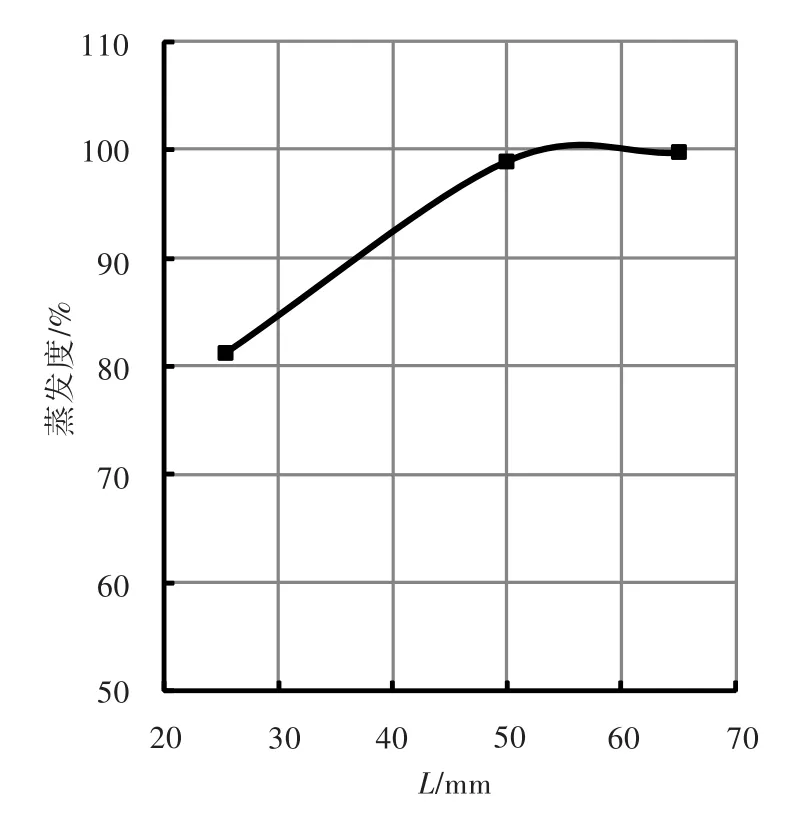
图7　燃油蒸发度随燃油喷射离钝体稳定器尾缘距离的变化（d=0.61 mm）Fig.7 Fraction evaporated of kerosene with different distance from the trailing edge（d=0.61 mm）

（3）堵塞比

保持钝体尾缘速度和气流温度不变，喷口直径固定为0.61 mm，喷射距离和燃油供给量一定。通过将钝体槽宽由31.8 mm逐渐增加到44.0 mm，使得钝体的堵塞比在0.21～0.29范围内，研究堵塞比对钝体回流区局部当量比的影响，结果见图8。由图可知：局部当量比随堵塞比呈现单峰形态。堵塞比由0.21增加到0.25时，回流区内局部当量比由1.71增加到1.84，增幅达7.6%；随着堵塞比进一步增加到0.29，回流区局部当量比略有下降。

（4）来流温度

图8　回流区当量比随钝体堵塞比的变化Fig.8 Comparison ofΦlwith various blockage ratios

保持钝体尾缘速度、喷口直径，喷射距离和燃油供给量一定，来流温度改变对钝体回流区内局部当量比的影响如图9所示。可见，回流区内当量比随气流温度的提高而增加。原因是随着温度的提高，燃油液滴的蒸发增强，使得进入回流区内的气态燃油量增加。从图中还可看到：总当量比越大，回流区内当量比随来流温度的变化越剧烈。这是因为在喷口直径一定的情况下，总当量比大意味着燃油喷射速度大，燃油的初始雾化液滴直径小，温度对燃油液滴的蒸发作用更明显。

图9　回流区当量比随来流温度的变化Fig.9 Comparison ofΦlwith different incoming flow temperature

（5）来流速度

保持来流温度、喷口直径，喷射距离和燃油供给量一定，来流速度改变对钝体回流区内局部当量比的影响如图10所示。由图可知：回流区内当量比随气流速度的增加而变大。这是因为：一方面，随着来流速度的提高，液滴与气流的动量比减小，使得液滴的穿透减弱，燃油更多地分布在钝体稳定器壁面附近；另一方面，速度的增加使得液滴初始阶段的二次雾化更强，燃油蒸发加速，使得气态燃油浓度增加。正是这两方面的原因增加了进入钝体回流区内的燃油流量，所以回流区内当量比随气流速度增加而变大的趋势很明显。

图10　回流区当量比随来流速度的变化Fig.10 Comparison ofΦlwith different incoming flow velocity

上述数值模拟结果表明，紧凑喷射模式下的气动参数和特征结构参数，主要从燃油雾化、蒸发、分布等方面影响钝体回流区内的局部当量比。文献［5］依据试验结果提出用综合参数EP来预估回流区内的局部当量比，见式（5）。该综合参数EP基于液气动量比J、喷口直径和钝体尾缘速度，见式（6）。

本文进一步考虑温度和喷射距离的影响，对综合参数EP进行完善，见式（7）。完善后的EP和Φl的关系及其拟合曲线如图11所示。

4　结论

通过数值模拟，研究了加力环境中紧凑喷射模式下钝体回流区内局部当量比的影响因素，并完善了影响钝体回流区内局部当量比的综合参数EP，建立了回流区局部当量比和综合参数值的简易拟合关系。各气动参数和特征结构参数对局部当量比的定性影响规律如下：

图11　回流区内局部当量比随综合参数EP的变化Fig.11 The changes ofΦlwith the parameter EP

（1）回流区内局部当量比随喷口直径的增加而增加；

（2）回流区内局部当量比先随喷射距离的增加而增加，但当距离大于一定值时，钝体回流区内局部当量比很接近；

（3）回流区内局部当量比随堵塞比呈现单峰形态；

（4）回流区内局部当量比随气流温度的提高而增大；

（5）回流区内局部当量比随气流速度的增加而增大。

［1］ Colket M B III，Spadaccini L J.Scramjet fuels autoignition study［R］.ISABE 99-7069，1999.

［2］ Wadia A R，James F D.F110-GE-129 EFE：enhanced power through low risk derivative technology［R］.ASME 2000-GT-0578，2000.

［3］ Lovett J，Cross C，Lubarsky E，et al.A review mechanisms controlling bluff-body stabilized flames with closely-cou⁃pled fuel injection［R］.ASME GT2011-46676，2011.

［4］ DeZubay E A.Characteristics of disk-controlled flames［J］. Aero Digest，61（1）：54—56.

［5］ Klusmeyer A，Cross C，Lubarsky E，et al.Prediction of blow-offsofbluff-bodystabilizedflamesutilizing close-coupled injection of liquid fuels［R］.ASME GT 2012-69025，2012.

Numerical simulation of local equivalence ratio in the bluff body recirculation zone utilizing close-coupled injection of liquid fuels

CAO Zong-hua，XIE Jian-guang，LI Feng，LIN Jian-fu
（China Gas Turbine Establishment，Chengdu 610500，China）

Aiming at the close-couple injection utilized by flame holders in advanced augmenters，a rectan⁃gle model including the bluff body was researched.The effects of incoming flow temperature，velocity，injec⁃tor diameter，injection orifices of the trailing edge and bluff body width on the local equivalence ratio in RZ （recirculation zone）were investigated.Numerical simulation indicates that the value of local equivalence ra⁃tio in RZ gets larger by increasing incoming flow temperature，velocity，injector diameter or bluff body width.The obtained data was used to develop a transfer function to predict the local equivalence ratio in the RZ based on the parameters.

aero-engine；afterburner；flame holder；close-couple injection；local equivalence ratio；numerical simulation

V231.2

A

1672-2620（2016）04-0022-05

2015-10-29；

2016-06-17

曹宗华（1983-），男，四川广安人，工程师，硕士，主要从事加力燃烧室设计。