几何因素对涡轮过渡段性能的影响
李同日,刘火星
(北京航空航天大学能源与动力工程学院,北京100191)
几何因素对涡轮过渡段性能的影响
李同日,刘火星
(北京航空航天大学能源与动力工程学院,北京100191)
为研究涡轮过渡段几何因素对其性能的影响,采用参数化方法进行过渡段子午流面造型,利用数值模拟方法对过渡段性能进行计算分析,同时借助试验结果予以对比验证。结果表明:长高比、扩张角会影响过渡段壁面曲率变化,大长高比、小扩张角过渡段扩压效果较好;相对于长高比、面积比,扩张角对过渡段总压恢复系数影响最大;进出口面积比直接影响过渡段扩压程度,但对过渡段总压损失影响较小;面积比增大18%,静压升系数最大可增加90%。
航空发动机;涡轮过渡段;几何因素;长高比;面积比;扩张角;数值模拟;试验测量
slope angle;numerical simulation;experimental measurement
1 引言
现代高性能航空发动机通常采用高转速和小轮毂比设计,以使核心机尺寸更小、质量更轻。对于连接高、低压涡轮的过渡段,涵道比增大必然导致其扩张角增加,同时其壁面曲率与面积比分布也必然随之改变。长高比、面积比和扩张角是过渡段设计中最重要的三个几何参数,决定着过渡段内部流动的基本特征,对涡轮过渡段性能起主导作用。
为深入研究几何因素对过渡段性能的影响,研究人员对简单扩压管道进行了详细的研究。Kline等[1]将扩压型管道分成无分离、小分离、大分离和超大分离4个体系,分析了几何因素对扩压管道内部流动的影响,表明小扩压率与小轴向压力梯度的扩压管道损失较小。在其基础上,Carlson等[2]试验和理论研究了扩压管道结构对扩压管道设计的影响,通过对比钟形、喇叭形及S形锥形扩压管道性能,得出端壁型线对优化设计扩压管道意义重大,从而衍生出现今常用的S形结构。
针对几何因素对S形过渡段性能的影响,国内外学者开展了大量研究。Kuchana等[3]对S形过渡段曲率分布变化的影响进行了数值模拟,得出将机匣壁面在第一个弯处的反弯点向下游移动,可减小或消除分离。Hu等[4]通过一系列系统的试验与数值模拟,探究了扩张角和面积比对四种不同几何参数涡轮过渡段的影响。结果表明,扩张角决定第一个弯处的逆压力梯度,面积比主要决定第二个弯处的静压升,压力损失随着中位角和面积比的增大显著增加。安柏涛等[5]采用数值方法对大扩张角中介机匣子午流道型线进行了改型设计,结果表明改变子午扩张形流道外壁型线对其出口能量损失影响较为显著。阙晓斌等[6]建立了S形过渡段流道几何的参数化描述方式,探讨了面积比分配对过渡段性能的影响,表明控制点面积比将显著改变壁面压力分布。
目前,国内外的研究趋势是,在设计上越来越趋向于大扩张角超紧凑结构,在试验方面越来越趋近于发动机实际工作条件。但这两方面的工作都开展得较少,并且对于几何因素对大扩张角过渡段性能影响的研究也不够深入。为此,本文通过构造涡轮过渡段子午流道型线,利用数值模拟方法,研究长高比、面积比、扩张角等几何参数对过渡段性能的影响,并借助试验进行对比验证。研究中,由于涡轮过渡段内流动具有轴对称的二维特征,故数值与试验方法均采用二维过渡段。
2 子午流道设计
涡轮过渡段子午流道设计是一个反复迭代的过程,具体包括总体几何参数选取、气动边界条件分析、支板叶型设计、流道型线设计和三维气动性能校核五个步骤。由于本文重点在于几何因素对涡轮过渡段性能影响的原理性探究,对设计初始几何参数选取较为自由,并忽略支板对过渡段性能的影响,加之收敛曲线具有光滑连续等特点,所以本文涡轮过渡段壁面型线采用常用的收敛曲线即可满足要求。
根据文献[7]中研究结果可知,过渡段前半段进口附面层厚度薄时大幅度增加面积比,随后在过渡段易分离区域减少面积比,可使流体加速抵制附面层分离。根据这一设计特点及计算验证,选取双三次样条曲线[8]作为轮毂面曲线、五次曲线作为机匣面曲线所设计的过渡段性能较好。涡轮过渡段设计参数和设计流程分别见图1、图2。图2中,公式(1)、公式(2)分别为:


式中:D11为入口轮毂面径向高度,D12为入口机匣面径向高度,D21为出口轮毂面径向高度,D22为出口机匣面径向高度,X为轴向距离,L为过渡段长度,y1为轮毂面径向坐标,y2为机匣面径向坐标。
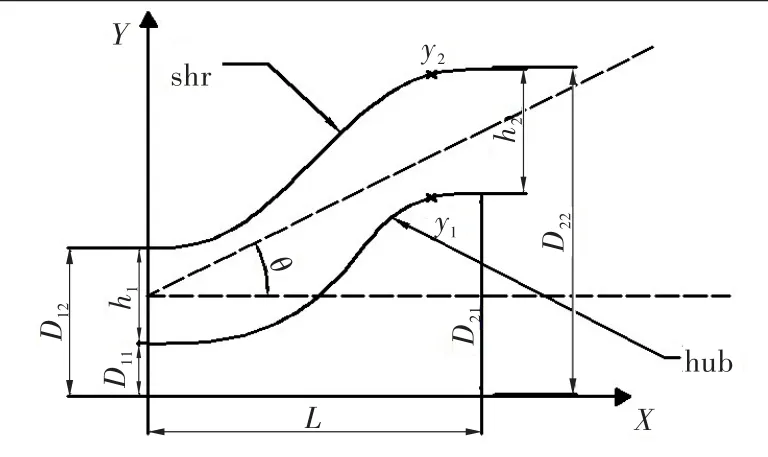
图1 过渡段设计参数Fig.1 ITD geometry parameters

图2 过渡段设计流程Fig.2 ITD design process
根据Sovran等[9]给出的环形扩张段性能参数及现有发动机过渡段几何参数可知,过渡段一般选取长高比(L/h1)1.5~3.5,面积比(AERO)1.1~1.5。Couey等[10]对扩张角(θ)27°~36°的过渡段做了较为详尽的研究,表明扩张角增大是过渡段未来的发展趋势,故本文将大扩张角过渡段作为研究对象。表1给出了过渡段初始设计几何参数。

表1 过渡段初始设计几何参数Table 1 ITD initial design parameters
3 数值方法
计算工具采用CFX12.1,计算模型为SST湍流模型,二阶差分格式。进口边界给定总压、静温及气流方向,出口边界给定静压,计算域进出口处均向两侧延伸。计算网格采用ICEM CFD生成,网格沿流向划分为六块(图3),保证网格与主流方向垂直,网格近壁处加密,边界条件为连续性周期边界。计算网格总数46万,径向网格节点61个,周向网格节点41个,沿流向网格节点145个。所有固壁附近无量纲化网格高度y+<2。数值计算网格拓扑结构见图4。
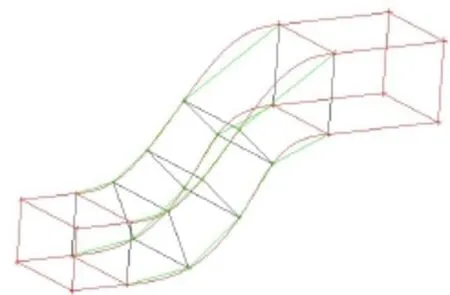
图3 网格分块结构Fig.3 Grid block structure
4 数值模拟结果
描述流体流经过渡段参数变化和过渡段性能的参数包括:
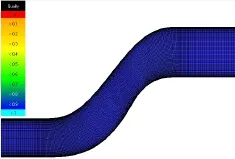
图4 数值计算网格拓扑Fig.4 Numerical mesh topology
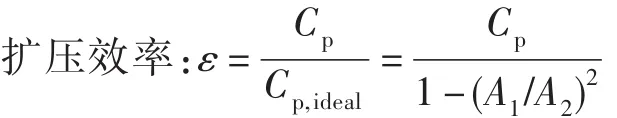
式中:p1为入口静压,p2为出口静压,pt1为入口总压,pt2为出口总压,A1为入口面积,A2为出口面积。

图5不同长高比对过渡段静压升系数及总压恢复系数的影响(AERO=1.3,θ=36°)Fig.5AERO=1.3,θ=36°,L/h1=2.5,3.0,3.5 different length height ratio impact on the extent of static pressure and total pressure recovery
图5给出了相同面积比和扩张角、不同长高比的三组过渡段的静压升系数和总压恢复系数子午面云图。图中,σL/h1=2.5表示长高比为2.5时的过渡段出口总压恢复系数,其余类似。从静压升系数云图中可看出,长高比增大,过渡段机匣面第一个弯处、轮毂面第二个弯处静压升系数变大,使机匣面沿程逆压力梯度及轮毂面近出口处逆压力梯度均变小。从总压恢复系数云图中可看出,流体在第一个弯处并没有发生分离,之后轮毂面经历一个较长顺压梯度,有利于抑制附面层发展;但在第二个弯处轮毂面经历一个强逆压力梯度,而机匣面经历逆压力梯度直到出口位置,轮毂、机匣面出口处有不同程度的总压损失。长高比增大,出口总压损失变大。
图6为相同长高比和扩张角、不同面积比三组过渡段的数值模拟结果。从静压升系数云图中可看出,对于小面积比过渡段,面积比增大会降低机匣面第一个弯折处的静压升系数,使机匣面逆压力梯度增大;但在第二个弯折处,机匣面静压升系数会随面积比的增大而减小,但减小程度随面积比的增大有降低的趋势。轮毂面第二个弯折处静压升系数随面积比的增大而变小,这将导致机匣面近出口处逆压较大,分离变大。面积比1.2、1.3的两组过渡段流动结构相似,与面积比1.1的过渡段有所不同。从总压恢复系数云图中可看出,面积比增大会造成过渡段机匣、轮毂面分离变大,使过渡段出口总压损失增大。
图7为相同长高比和面积比、不同扩张角的三组过渡段数值模拟结果。从静压升系数云图中可看出,对于大扩张角过渡段,增大扩张角将造成过渡段第一个弯折处曲率增大,使流体在轮毂面加速更加剧烈;机匣面处静压升系数较低,逆压力梯度增大,过渡段机匣面分离风险增大。对于轮毂面,在第二个弯折处,扩张角的增大也使过渡段静压升系数降低,使近轮毂面分离加剧。从总压恢复系数云图中可看出,扩张角增大将导致过渡段总压损失区域扩大,使过渡段总压损失增大。
为表征几何参数对过渡段性能参数的影响趋势,图8示出了27组不同几何参数过渡段的静压升系数和总压恢复系数模拟结果平均值。可见,相对于扩张角、长高比,面积比对过渡段静压升系数的影响更大。减小扩张角有利于降低机匣面进口处凸曲率值,增大长高比能减缓过渡段曲率沿程变化,而曲率对过渡段壁面静压升系数的影响特别大,所以小扩张角、大长高比过渡段扩压效果较好。而根据流量守恒和动量守恒,进出口面积比直接影响过渡段扩压效率,所以面积比增大将较大幅度提升过渡段扩压效果。针对本文所设计的过渡段,面积比增大18%,静压升系数最大可增加90%。对于总压恢复系数,长高比、面积比变化对其的影响类似,但扩张角对总压损失影响较大。因此,对于大扩张角过渡段,扩张角对于总压损失影响至关重要。而对于面积比,较大的面积比使过渡段后半段流体加速较小,抑制附面层分离较弱,所以总压损失较大。

图6 不同面积比对过渡段静压升系数及总压恢复系数的影响(L/h1=3.0,θ=36°)Fig.6L/h1=3,θ=36°,AERO=1.1,1.2,1.3 different area ratio impact on the extent of static pressure and total pressure recovery
5 试验方法
为验证数值方法的准确性,对试验件A(长宽比3.5、面积比1.3,扩张角36°)和试验件B(长宽比3.5、面积比1.3,扩张角40°)两个过渡段进行试验研究。测量内容包括垂直流向截面处静压、总压、速度分布以及过渡段上下端壁静压分布。试验进口马赫数0.5,进口径向高度50 mm,周向长度80 mm。出口截面测点143个,近上下壁面处加密。沿流向设5个测量截面,出口截面与s5界面重合。前4个截面测点各16个,各截面位置如图9所示。上下端壁静压孔沿过渡段流向中央垂直壁面打孔,各21个。

图7 不同扩张角对过渡段静压升系数及总压损失系数的影响(L/h1=3.5,AERO=1.3)Fig.7L/h1=3.5,AERO=1.3,θ=36°,40°,44°different slope angle impact on the extent of static pressure and total pressure recovery

图8 几何因素对静压升系数和总压恢复系数影响平均趋势Fig.8 The effects of geometrical factors on the extent of static pressure and total pressure recovery average
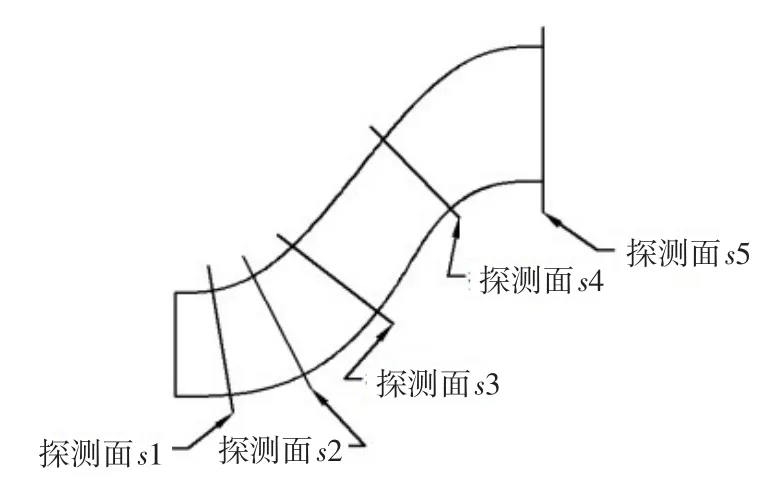
图9 沿流向各截面位置Fig.9 Cross-section position along the flow
6 试验测量结果
图10展示了不同扩张角过渡段上下端壁静压升系数模拟与试验结果的对比。可见,机匣面静压力梯度首先为顺压梯度,到15%位置后为一强逆压力梯度,极易引起附面层分离;轮毂面压力梯度首先为一逆压力梯度,然后是一较强顺压力梯度,最后在近出口处经历一强逆压力梯度。轮毂面的数值模拟结果与试验结果符合较好;机匣面前半部分数值模拟结果与试验结果拟合较好,但后半部分有所偏差。这是因为机匣面在整个过渡段流动区域中大部分是逆压力梯度,有分离产生,而数值模拟不能很好地预测分离。总体而言,机匣面分离导致的偏差较小。
表2为试验件A、B总压恢复系数(出口总压与进口总压之比)试验与数值结果对比。可见,试验件A、B数值计算与试验得出的总压恢复系数符合性较好,本文所采用的数值计算能较为准确地模拟涡轮过渡段真实工作情况;扩张角增大,总压恢复系数有所降低。
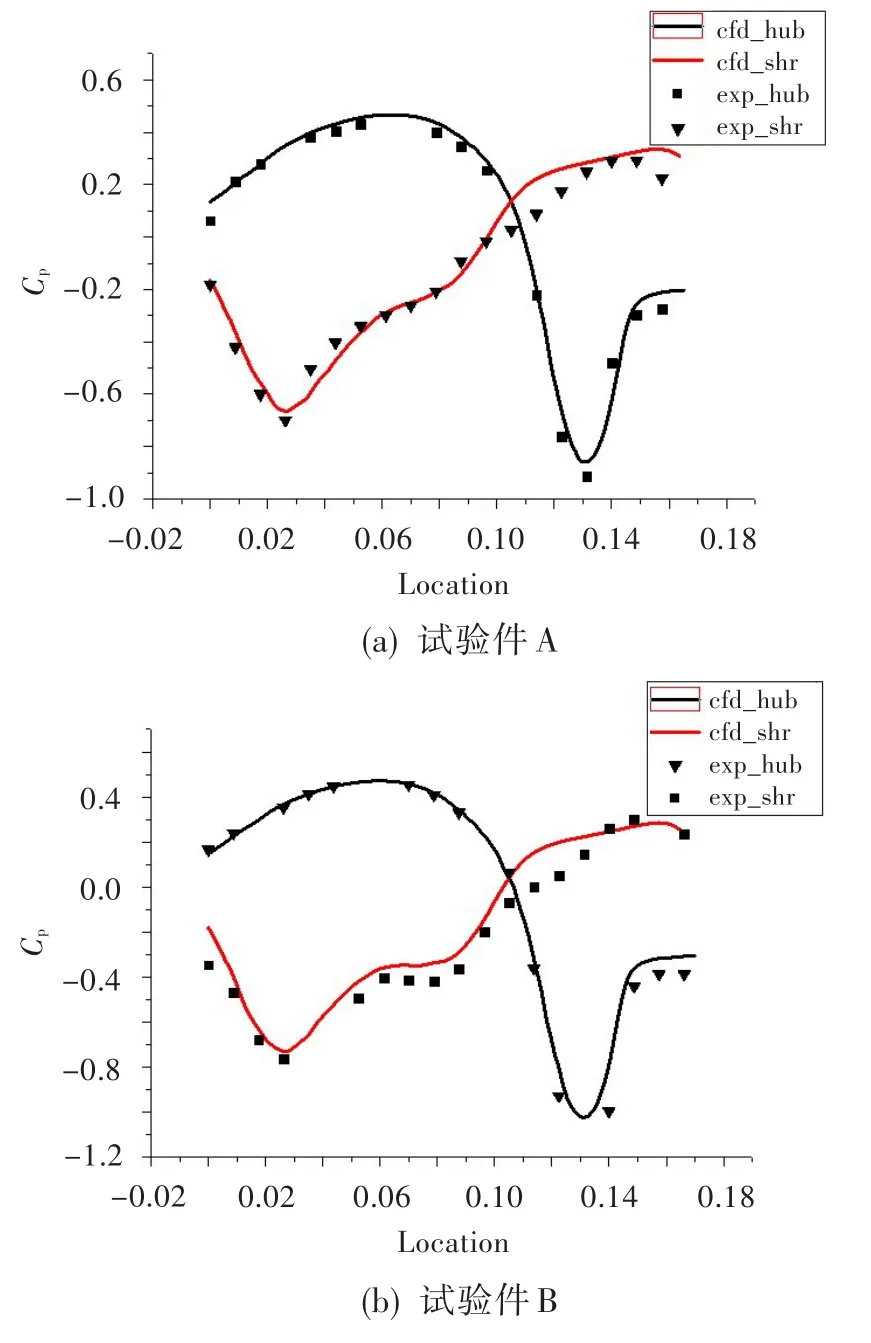
图10 试验件上下壁面静压升系数数值模拟与试验结果对比Fig.10 Comparison between shroud wall static pressure recovery coefficient numerical simulation and test results

表2 试验件A、B总压恢复系数计算值与试验值的对比Table 2 Total pressure recovery coefficient comparison between calculation and test results of testing pieces A,B
图11为试验件A、B沿流向各截面的马赫数分布图。根据流线曲率法,凸曲率使流体加速,凹曲率使流体减速。由图可看出,在过渡段第一个弯折处机匣面是凸曲率,轮毂面为凹曲率,在s1截面处,马赫数沿径向分布呈轮毂低机匣高的形态。s2截面的分布方式和s1类似。s3截面近机匣面10%高度范围内存在低速区,且马赫数沿径向差值有所减小。s4截面为过渡段第二个弯折处,此时轮毂面为凸曲率,机匣面为凹曲率,使马赫数沿径向分布呈轮毂高机匣低的趋势,同时近机匣面低速区域范围变大。到s5截面,低速区出现在近轮毂面20%高度范围内。

图11试验件沿流向各截面的马赫数分布Fig.11 Mach number distribution on cross sections along the flow direction
图12为试验件A、Bs2截面和s5截面处马赫数分布。可看出扩张角变大,过渡段在第一个弯折处曲率增大,流体从轮毂面到机匣面加速剧烈。对比试验件s5截面马赫数分布,由于轮毂面出口处强逆压梯度,近轮毂面有分离的趋势。且随着扩张角的增大,过渡段第二个弯折处曲率变大,逆压程度更强,近轮毂面分离也更加剧烈。
图13为试验件A、B沿流向各截面总压恢复系数分布。可见,过渡段前半段总压恢复系数变化不大,但从s4截面开始,由于附面层的发展导致流体有分离的趋势,使近出口处总压损失增大,总压恢复系数沿截面减小。扩张角增大,逆压程度增大,出口近轮毂面分离程度更加剧烈,导致出口截面处总压恢复系数变化较大。

图12 试验件s2和s5截面的马赫数分布Fig.12 Mach number distribution ons2ands5cross sections
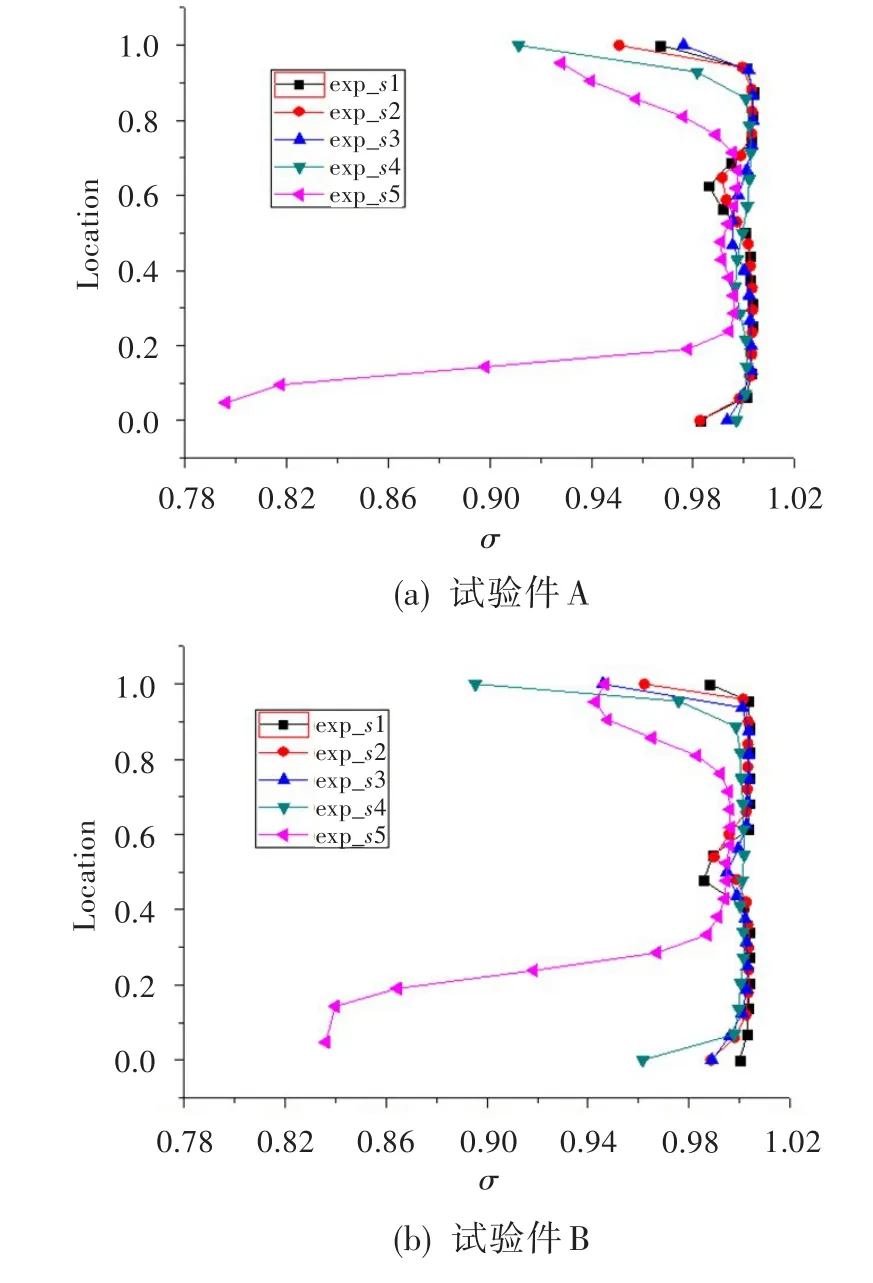
图13 试验件沿流向各截面总压恢复系数分布Fig.13 Total pressure recovery coefficient distribution on cross sections along the flow direction
7 结论
(1)长高比、扩张角影响过渡段壁面曲率变化,大长高比、小扩张角过渡段扩压效果较好。
(2)进出口面积比直接影响过渡段扩压程度。针对本文所研究的过渡段,面积比增大18%,静压升系数最大可增加90%。
(3)相比于长高比、面积比,扩张角对过渡段总压损失的影响更大。扩张角变大,将造成过渡段机匣面第一个弯折处、轮毂面第二个弯折处曲率增大,导致逆压梯度变大,附面层发展剧烈,分离程度加剧,总压损失增大。
[1] Kline S J,Abbott D E,Fox R W.Optimum design of straight walled diffusers[J].Journal of Basic Engineering,1959,81:321—330.
[2] Carlson J J,Johnston J P,Sagi C J.Effects of wall shape on flow regimes and performance in straight two-dimen⁃sional diffusers[J].Journal of Basic Engineering,1967,89:151—160.
[3] Kuchana V,Guntu S,Srinivasan B,et al.Numerical study on inter-turbine ducts with variable curvature distribution [R].AIAA 2013-3686,2013.
[4] Hu S Z,Zhang X F,Benner M,et al.Geometric optimiza⁃tionofaggressiveinter-turbineducts[R].ASME IMECE2010-37323,2010.
[5] 安柏涛,韩万金,王松涛,等.大扩张角子午流道型线对损失的影响[J].推进技术,2001,22(3):211—214.
[6] 阙晓斌,侯安平,周盛.基于壁面压力梯度控制的压气机S形过渡段设计[J].航空学报,2010,31(3):460—465.
[7] Zhang X F,Hu S Z,Benner M G,et al.Experimental and numerical studyonaninter-turbineduct[R].ASME IMECE2010-37322,2010.
[8] 潘锦珊,单鹏.气体动力学基础[M].北京:国防工业出版社,2011.
[9] Sovran G,Klomp E D,Experimentally determined opti⁃mum geometries for rectilinear diffusers with rectangular,conical or annular cross-section[M].USA:General Motors Corporation Research Publication,1965.
[10]Couey P T,McKeever C W,Malak M F,et al.Computa⁃tional study of geometric parameter influence on aggres⁃siveinter-turbineductperformance[R].ASME GT2010-23604,2010.
Study of geometric factor influence on inter-turbine duct performance
LI Tong-ri,LIU Huo-xing
(School of Energy and Power Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
To study the influence of geometric factors on the inter-turbine duct(ITD)performance,a para⁃metric method for inter-turbine duct meridional flow surface modeling was adopted,and numerical method was used to calculate and analyze the performance,and then compared with experimental results.The re⁃sults show that length height ratio and the area ratio will influence the changes of wall curvature in the in⁃ter-turbine duct.Large length height ratio and small slope angle have better diffuser effect.Compared with length height ratio and area ratio,slope angle has more effects on the total pressure recovery coefficient of ITD.Area ratio directly influences the extent of the pressure in the inter-turbine duct,but the total pressure loss is less affected.Static pressure recoverywill increase 90 percent when area ratio increases 18 percent. Key words:aero-engine;inter-turbine duct;geometric factors;length height ratio;area ratio;
V231.3
A
1672-2620(2016)04-0006-07
2015-09-17;
2015-11-10
李同日(1990-),男,黑龙江伊春人,硕士研究生,从事涡轮过渡段性能计算与试验研究。

