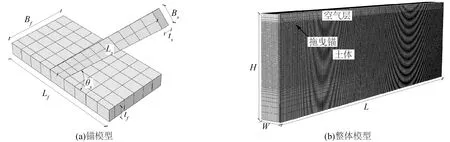
拖曳锚在海床中运动特性的大变形有限元分析
李培冬,刘海笑,赵燕兵
(天津大学 建筑工程学院,天津 300072)
拖曳锚在海床中运动特性的大变形有限元分析
李培冬,刘海笑,赵燕兵
(天津大学 建筑工程学院,天津 300072)
拖曳锚由于其承载性能和深水中便于安装被广泛应用于海洋工程系泊系统中,如:适用于悬链式系泊系统的传统拖曳锚和适用于绷紧式系泊系统的法向承力锚。拖曳锚安装过程中涉及诸多运动特性:锚板运动方向、系缆点处拖曳力和拖曳角及运动轨迹。基于大变形有限元分析技术耦合的欧拉-拉格朗日法,并引入缆绳方程,建立起锚-缆绳-海床土耦合作用的有限元分析模型;模拟了拖曳锚在均质和线性强度黏土中的嵌入安装过程,研究了锚板运动方向、系缆点处拖曳力和拖曳角及运动轨迹等运动特性;通过与已有的有限元分析方法及理论方法进行对比,验证了该分析模型的有效性;与已有的有限元分析方法相比,提出的分析模型有效地提高了计算效率。
拖曳锚;运动特性;耦合的欧拉-拉格朗日法;缆绳方程;大变形有限元
Abstract:Because of better performance both in pullout capacity and deepwater installation,drag anchors are widely utilized in mooring systems for offshore applications,such as the conventional drag anchor in the catenary mooring system and the vertically loaded plate anchor in the taut-wire mooring system.The penetration behaviors,such as the movement direction of the fluke,the drag force and drag angle at the shackle and the trajectory,are involved during the anchor installation.A large deformation finite element analysis using a coupled Eulerian-Lagrangian approach is performed to simulate the installation process of drag anchors in the clay with uniform and linear strengths,in which a chain equation is introduced to reflect the interaction between the installation line and the anchor.By comparing the results of the published FE method and theoretical method,including the movement direction of the fluke,the drag force and drag angle at the shackle and the trajectory,the efficiency of present work is well verified.Compared with the published FE method,the FE model of present work has a better performance in computational efficiency.
Keywords:drag anchor; kinematic behavior; coupled Eulerian-Lagrangian; chain equation; large deformation FE method
随着海洋油气开发不断向深水及超深水发展,大型浮式海洋平台及适用于深水油气开发的绷紧式系泊方式得到了日趋广泛的应用,同时也对深水系泊系统提出了更高的要求。法向承力锚具有承载性能优异和便于深水安装的特点,因而被广泛应用在深水系泊系统中[1]。
法向承力锚与传统拖曳锚的安装方式基本相同,拖曳锚与拖船通过缆绳连接,拖曳锚被抛锚至海床面后,拖船沿一定方向移动,拖曳锚逐渐嵌入海床土直至目标深度,同时锚板方位角逐渐减小[1]。在拖曳锚的整个安装过程中,缆绳形态及通过缆绳传递的拖曳力也在不断发生变化。拖曳锚安装完成后,其承载性能高度依赖于最终嵌入深度和锚板方位角。嵌入深度和锚板方位角由拖曳锚的运动轨迹决定,而运动轨迹在安装过程中是不可见的,因此研究锚的嵌入运动轨迹具有重要意义。
拖曳锚嵌入过程中,除运动轨迹[2-5]外,还涉及诸如锚板运动方向[6-8]、系缆点处拖曳力[9-11]和拖曳角[2,7,11]等运动特性,这些运动特性直接影响锚的嵌入运动轨迹。目前,针对拖曳锚运动特性的研究主要包括数值增量求解法、理论解析法和试验研究,Zhang[1]对此作了详细的总结。随着有限元技术的发展,越来越多的研究者将有限元技术应用于锚的数值分析中,但对于拖曳锚运动特性的研究较少。有限元分析拖曳锚运动特性有两个难点:其一,锚与土体的耦合作用会使土体产生极大变形,传统的有限元方法在模拟大变形问题时会产生网格畸变,甚至出现计算不收敛的情况;其二,在安装过程中根据缆绳形态可以把缆绳分成悬链缆、卧底缆及嵌入缆三部分[4],嵌入缆形成的反悬链形态对拖曳锚的嵌入性能影响显著,在有限元分析中必须采用恰当的方法来模拟嵌入缆的反悬链特性。
Zhao和Liu[12]基于大变形有限元分析技术耦合的欧拉-拉格朗日法(coupled Eulerian-Lagrangian,CEL),建立了能够模拟拖曳锚在海床土中嵌入安装过程的有限元分析模型。CEL法克服了传统有限元方法在模拟大变形问题时常见的接触问题和网格畸变问题。通过与已有理论预测结果对比,验证了CEL法分析拖曳锚运动特性的有效性。为模拟嵌入缆的反悬链特性,Zhao和Liu通过LINK连接单元连接柱形块体来构建安装缆绳,安装缆绳与锚之间同样通过LINK连接单元连接。对比结果验证了这种方法在模拟嵌入缆反悬链特性时的有效性[12,13],但缺点在于:缆绳的存在使得模型的网格规模扩大,由此导致模型的计算效率较低。因此,提出一种能够有效提高计算效率的分析模型势在必行。
本文基于大变形有限元分析技术耦合的欧拉-拉格朗日法,引入缆绳方程,建立锚-缆绳-海床土耦合作用的有限元分析模型。其中,系缆点处缆绳与锚的相互作用由缆绳方程来描述,并通过ABAQUS用户子程序VUAMP来实现。分析模型模拟了拖曳锚在均质和线性强度黏土中的嵌入安装过程,研究了锚板运动方向、系缆点处拖曳力和拖曳角及运动轨迹等运动特性。通过与已有的有限元分析方法进行对比,来验证该分析模型的有效性和在计算效率方面的优势。
1 数值方法
1.1耦合的欧拉-拉格朗日法(CEL)
有限元分析中,描述物体运动和变形的方法有两种:拉格朗日法和欧拉法。拉格朗日法(Lagrangian)是一种网格依附于材料的计算方法,网格随材料变形而变形。网格内充满单一材料,能够很好地追踪材料边界的变化。但对于大变形问题,网格会发生严重变形,将导致计算不收敛。欧拉法(Eulerian)采用网格固定而材料可在网格中自由流动的方式,网格不随材料变形而变形,克服了拉格朗日法网格畸变所带来的数值奇异,但欧拉法不能很好地追踪材料边界的变化。
为了克服传统有限元法的缺陷,大变形有限元法CEL被提出。该方法最先由Noh[14]提出,Benson和Okazawa[15,16]又进一步将其完善。CEL法集合了欧拉算法和拉格朗日算法的优点。在分析土和结构物耦合作用时,土体采用欧拉算法,即网格固定,土体在网格中流动,不存在网格畸变问题。通过计算每个单元的欧拉材料体积分数(EVF)来追踪土体在网格中的流动变形,EVF=1表示网格被土体填满,EVF=0表示网格中没有土体。结构采用拉格朗日算法,通过结构的边界来追踪土与结构接触面的变化。目前,CEL法已经被广泛应用于模拟结构物与土体耦合作用的大变形问题[12,17-20]。
1.2子程序VUAMP
有限元软件ABAQUS提供了FORTRAN语言编写的子程序接口,供用户根据需求进行二次开发。为了克服直接构造安装缆绳造成的计算耗时,本文通过缆绳方程来描述系缆点处缆绳与锚的相互作用,即在拖曳锚系缆点处施加不断变化的拖曳力。VUAMP子程序接口使得用户可以定义相关变量的幅值曲线,如载荷条件、边界条件和预定义场等,描述这些变量随时间或位移等参数的变化情况[21]。
为了实现在拖曳锚系缆点处施加不断变化的拖曳力,需要定义集中载荷随时间变化的幅值曲线。现以本文所研究问题为例,介绍VUAMP使用过程中的关键技术:
1)定义与集中载荷(拖曳力)相关的历史输出变量,并通过传感器(Sensor)将相应的输出变量传递给子程序VUAMP,用于计算下一增量步的载荷值。拖曳锚系缆点处拖曳力与系缆点的水平和竖向位移相关,因此,需将系缆点的水平和竖向位移作为输出变量;
2)创建集中载荷(拖曳力),并定义相应的用户幅值(User amplitude),在定义用户幅值时指定所需状态变量(Svars)的数目,状态变量用于在两次调用子程序间传递变量;
3)ABAQUS在每个增量步(Increment)计算开始时,读取子程序VUAMP设置的幅值,进而更新系缆点处的集中载荷(拖曳力)。
2 数值方法流程
2.1缆绳方程
如图1所示,缆绳嵌入海床土中的部分,即嵌入缆,由于土抗力和摩擦力的共同作用形成反悬链形态。嵌入缆与锚在系缆点处发生相互作用,通过缆绳传递的拖曳力Ta以及拖曳力与水平方向的夹角θah直接影响锚在海床土中的运动特性。拖曳锚安装过程中,θah和Ta逐渐增大,使得作用在锚上的竖向力逐渐增大,促使锚板逐渐抬平。本文通过引入缆绳方程来模拟缆绳与土、缆绳与锚的耦合作用。
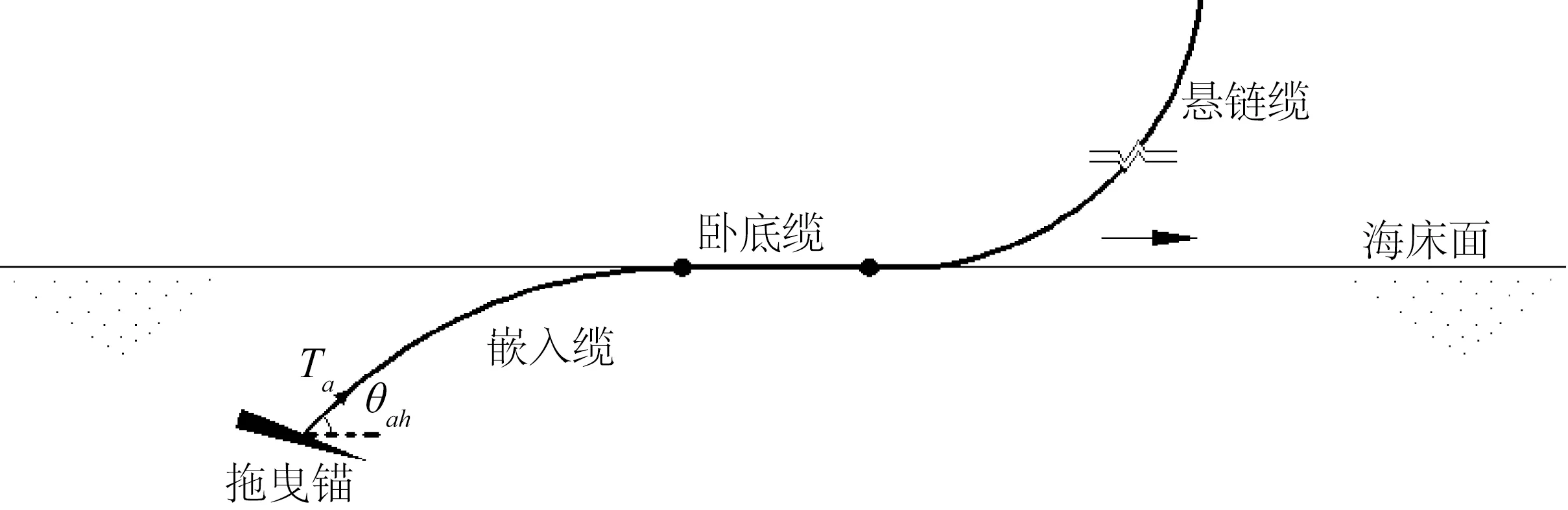
图1 安装缆绳示意Fig.1 Definition of installation line
Neubecker和Randolph[10]、Zhang等[11]提出了系缆点处拖曳力Ta与θah的关系式:
式中:μ为缆绳-土摩擦系数,在饱和黏土中,Neubecker和Randolph[10]、Zhang等[11]分别建议μ取0.4~0.6和0.1~0.6,DNV[22]建议钢缆取0.1~0.3,铁链取0.6~0.8;θ为某一深度z处缆绳与水平面的夹角;za为系缆点深度;En为有效承载系数,对于拖缆,Degenkamp等[23]基于模型试验,建议钢缆取1,铁链取2.5;d为缆绳直径;Nc为缆绳端阻力系数,取值范围为7.6~14[22-25];su为土体不排水抗剪强度,表示为:
式中:su0为海床面土体强度;k为土体强度梯度,对于均匀土,k=0。
对式(1)由海床面到系缆点深度za积分得:
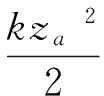
式中:θe为海床面处缆绳与水平面的夹角,本文假设拖曳锚安装过程中海床面处始终存在卧底缆,即θe=0°。随着拖曳锚的不断嵌入,系缆点处拖曳力Ta逐渐增大,通过式(3)求解相应的θah,然后在分析模型中将Ta以与水平面成一定角度θah的方式施加在系缆点处,从而直接影响拖曳锚的运动行为。
2.2实施流程
由于ABAQUS中只能加载水平和竖向载荷,因此,将作用在系缆点的拖曳力Ta沿水平方向和竖直方向分解(如图2),载荷值由式(4)决定。Tx和Tz在嵌入过程中不断变化,需要通过子程序VUAMP定义Tx和Tz随嵌入过程变化的幅值曲线。式(4)中的θah为拖曳力与水平方向的夹角,在子程序中通过式(3)更新。
有限元模型的分析流程如下:
1)给定初始时刻拖曳锚系缆点处的拖曳力Ta0和拖曳角θah0;
2)由式(4)计算作用在系缆点处的水平和竖向集中载荷及载荷幅值;
3)执行一个增量步计算,在下一个增量步计算开始之前调用子程序VUAMP,提取系缆点深度z,并利用式(3)计算新的θahi;
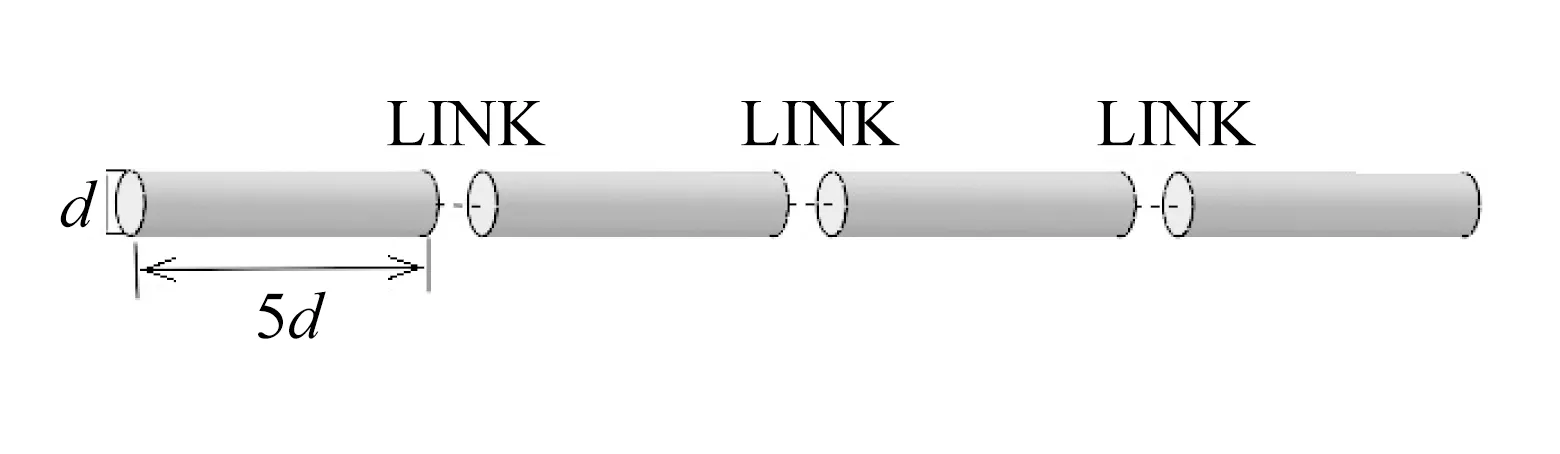
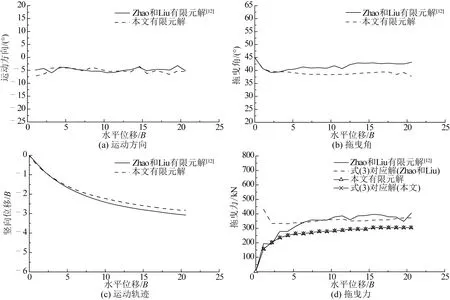
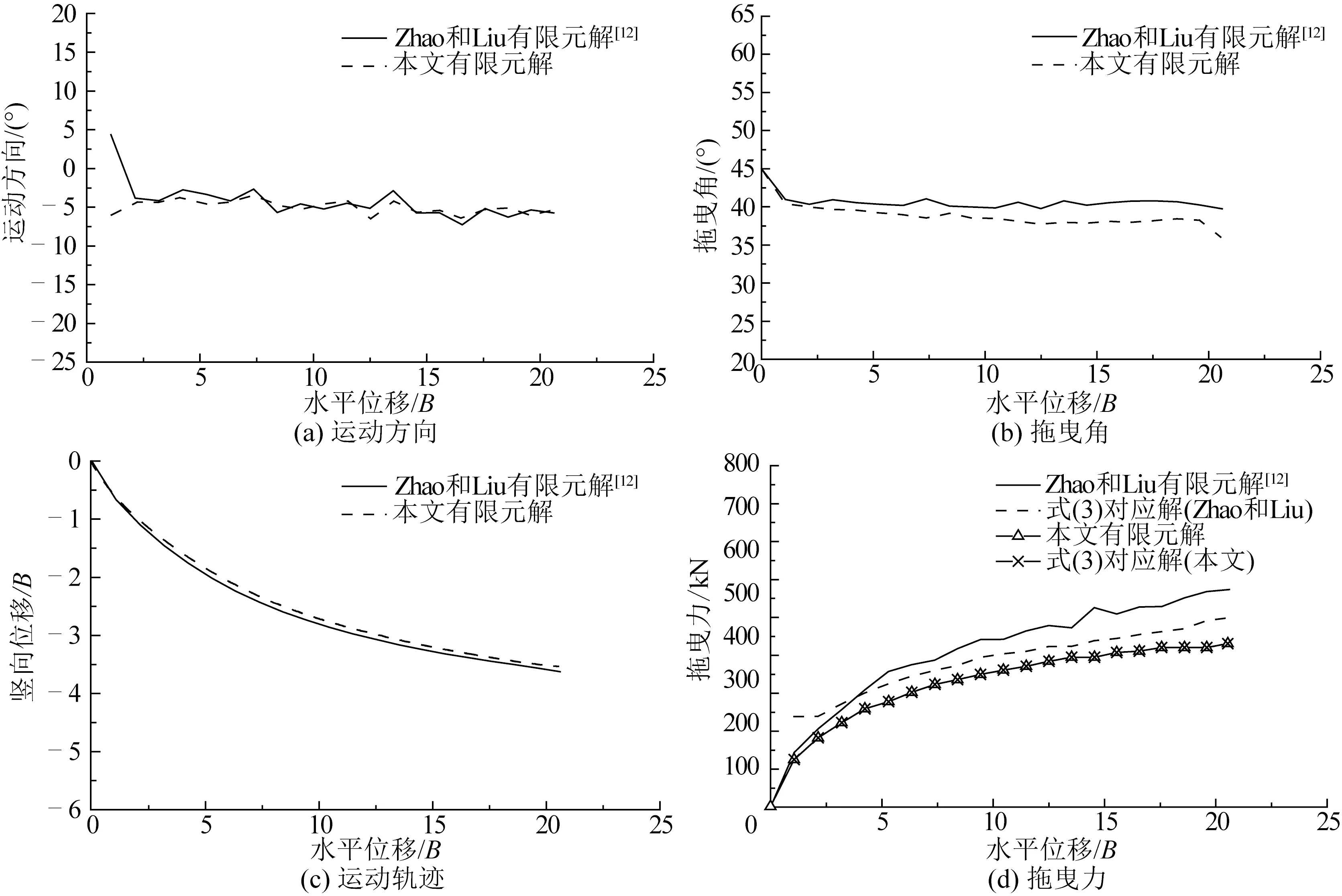
4)每隔一定时间tc,计算该段时间内系缆点水平运动的平均速度vd,比较控制速度vc和vd的相对大小,用于判断是否更新系缆力。若vd≥vc,保持系缆力不变;若vd 5)判断锚是否达到极限嵌入条件,是则停止计算,否则重复执行2)~5)。 整个分析流程在ABAQUS中通过调用子程序实现,不需要人为干预。在下文分析模型的验证中,tc取0.01 s,vc取0.5 m/s,初始时刻系缆力Ta0取1kN,θah0取0°,每次更新系缆力时ΔT取0.1kN。 图2 系缆点处拖曳力Fig.2 Drag force at the shackle 图3 安装缆绳模型[12]Fig.3 The installation line in the model[12] 为检验本文提出的有限元分析模型,将其应用于模拟拖曳锚在均质和线性强度黏土中的嵌入安装过程,分析嵌入过程中锚板运动方向、系缆点处拖曳力和拖曳角及运动轨迹等运动特性,并与Zhao和Liu[12]的有限元分析结果对比。Zhao和Liu通过LINK连接单元连接柱形块体来构建安装缆绳,如图3所示,由此来模拟嵌入缆在海床土中的反悬链特性,缆绳的存在严重降低了模型计算效率。本文通过引入式(3)来模拟缆绳与土、缆绳与锚的耦合作用,从而提高模型计算效率。 3.1数值模型 图4 有限元模型Fig.4 FE model 本文通过缆绳方程来模拟缆绳与土、缆绳与锚的耦合作用,见式(3)。式(3)中参数的取值均与Zhao和Liu一致,具体取值见表3。由于不对缆绳建模,本文分析模型的网格规模较Zhao和Liu的小,有效提高了模型的计算效率。 表1 拖曳锚模型参数Tab.1 Parameters for anchor in the model 表2 土体模型参数Tab.2 Parameters for soil in the model 表3 方程(3)所涉及参数Tab.3 Parameters in Eq.3 3.2均质土工况对比 图5 均质土工况对比Fig.5 Comparison of results in uniform clay 系缆点处拖曳力在工程上同样值得关注。图5(d)表明,本文求得的拖曳力与Zhao和Liu的计算结果在整体趋势上一致,但本文计算结果较Zhao和Liu的小。为了说明两者的差异,将采用理论解(即式(3))与两种有限元解进行对比,Neubecker和Randolph[10]及Zhang等[11]已分别通过试验验证了式(3)的有效性。式(3)中参数(θah,za)分别取自Zhao和Liu及本文的有限元解,得到两种有限元解对应的理论解,如图5(d)所示。由于本文求得的za小于Zhao和Liu的(见图5(c)),使得本文对应式(3)的解小于Zhao和Liu的;本文求得的拖曳力与式(3)完全吻合,Zhao和Liu的有限元解较式(3)大,增大了两种有限元解的差距。 Zhao和Liu有限元模型中引入的缆绳长37.8 m,土体网格单元数为875 420,本文模型通过引入缆绳方程减小了土体尺寸,土体网格单元数为575 276,较前者减少了34.3%。所使用的计算机配有2颗Intel E5-2690 v2处理器,32G内存。前者的CPU计算时间为50.2 h,本文模型计算时间较前者减少36.7%,有效提高了模型的计算效率。对于前者,如果引入更长的缆绳,土体网格单元数会相应增加,使得模型计算时间更长,此时本文有限元模型在计算效率方面的优势将更明显。 3.3线性土工况对比 本文线性土土体强度su=5+1.5zkPa,其余条件和均质土工况保持一致,计算结果如图6所示。 图6 线性土工况对比Fig.6 Comparison of results in the clay with linear strength 图6(d)表明,本文求得的拖曳力与Zhao和Liu的计算结果在整体趋势上一致,本文有限元解较小,造成两者差异的原因与均质土中的一致。对比图5(d)和图6(d)可以发现,线性土中拖曳力随着嵌入深度增加而线性增加,而均质土中拖曳力却逐渐趋于稳定,这是因为作用在锚上的土抗力和土体强度密切相关。 本文有限元模型的计算时间比Zhao和Liu的减少了41.6%,计算效率较均质土工况提高更多。 1)本文基于大变形有限元分析技术耦合的欧拉-拉格朗日法,引入缆绳方程,建立了锚-缆绳-海床土耦合作用的有限元分析模型,其中,系缆点处缆绳与锚的相互作用由缆绳方程来描述,并通过ABAQUS用户子程序VUAMP来实现。 2)分析模型模拟了拖曳锚在均质和线性强度黏土中的嵌入安装过程,研究了锚板运动方向、系缆点处拖曳力和拖曳角及运动轨迹等运动特性。通过与Zhao和Liu的有限元分析方法对比表明:本文分析模型求得的锚板运动方向与Zhao和Liu的相同;拖曳角稍小于Zhao和Liu的计算结果,均匀土和线性土中分别相差2.4°和1.7°;拖曳角越小锚的嵌入深度越浅,因此导致锚的嵌入深度也稍浅于Zhao和Liu的计算结果,均匀土和线性土中分别相差6.5%和3.4%;由于嵌入深度较小,使得本文求得的拖曳力小于Zhao和Liu的,而Zhao和Liu的有限元解大于式(3)的理论解,增大了两种有限元解的差距。 3)由于不对缆绳建模,本文有限元模型的网格规模比Zhao和Liu建立的模型要小,使得均质土中本文有限元模型的计算时间比Zhao和Liu的减少36.7%,线性土中减少41.6%,有效提高了计算效率,且拖曳缆绳越长本文有限元模型在计算效率方面的优势将更明显。 通过引入缆绳方程来描述系缆点处缆绳与锚的相互作用,模型的简化在提高计算效率的同时使得本文有限元解与Zhao和Liu存在一定差异,通过合理分析产生差异的原因,证明了本文所提分析模型的可行性。 [1] ZHANG W.Penetration mechanism and kinematic behavior of drag anchors[D].Tianjin:Tianjin University,2011. [2] AUBENY C P,MURFF J D,KIM B M.Prediction of anchor trajectory during drag embedment in soft clay[J].International Journal of Offshore Polar Engineering,2008,18(4):314-319. [3] MURFF J D,RANDOLPH M F,ELKHATIB S,et al.Vertically loaded plate anchors for deepwater applications[C]//Proceedings of International Symposium on Frontiers in Offshore Geotechnics.2005:31-48. [4] LIU H X,LIU C L,YANG H T,et al.A novel kinematic model for drag anchors in seabed soils[J].Ocean Engineering,2012,49:33-42. [5] LIU H X,LIU C L,ZHAO Y B,et al.Reverse catenary equation of the embedded installation line and application to the kinematic model for drag anchors[J].Applied Ocean Research,2013,43:80-87. [6] DUNNAVANT T W,KWAN C T T.Centrifuge modeling and parametric analyses of drag anchor behavior[C]//Proceedings of the 25th Offshore Technology Conference.1993:OTC7202. [7] O’NEILL M P,BRANSBY M F,RANDOLPH M F.Drag anchor fluke-soil interaction in clays[J].Canadian Geotechnical Journal,2003,40(1):78-94. [8] LIU H X,ZHANG W,LIU C L,et al.Movement direction of drag anchors in seabed soils[J].Applied Ocean Research,2012,34:78-95. [9] REESE L C.A design method for an anchor pile in a mooring system[C]//Proceedings of the 5th Annual Offshore Technology Conference.1973:OTC1745. [10] NEUBECKER S R,RANDOLPH M F.Profile and frictional capacity of embedded anchor chains[J].Journal of Geotechnical Engineering,1995,121:797-803. [11] ZHANG W,LIU H X,ZHAO Y B,et al.Interactional properties between drag anchor and installation line[J].Journal of Geotechnical and Geoenvironmental Engineering,2014,140(2):04013018. [12] ZHAO Y B,LIU H X.Numerical simulation of drag anchor installation by a large deformation finite element technique[C]//Proceedings of the 33rd International Conference on Ocean,Offshore and Arctic Engineering.2014:OMAE2014-23476. [13] ZHAO Y B,LIU H X.Large deformation finite element analysis of the anchor line embedded in seabed soils[C]//Proceedings of the 32nd International Conference on Ocean,Offshore and Arctic Engineering.2013:OMAE2013-10586. [14] NOH W F.A time-dependent two-space-dimensional coupled Eulerian-Lagrangian code[J].Methods in Computational Physics,1964,3:117-179. [15] BENSON D J.Computational methods in Lagrangian and Eulerian hydrocodes[J].Computer Methods in Applied Mechanics and Engineering,1992,99(2-3):235-394. [16] BENSON D J,OKAZAVA S.Contact in a multi-material Eulerian finite element formulation[J].Computer Methods in Applied Mechanics and Engineering,2004,193(39-41):4277-4298. [17] LIU H X,ZHAO Y B.Numerical study of the penetration mechanism and kinematic behavior of drag anchors using a coupled Eulerian-Lagrangian approach[J].Geotechnical Engineering,2014,45(4):29-39. [18] QIU G,HENKE S.Controlled installation of spudcan foundation on loose sand overlying weak clay[J].Marine Structures,2011,24(4):528-550. [19] QIU G,HENKE S,GRABE J.Application of a coupled Eulerian-Lagrangian approach on geomechanical problems involving large deformations[J].Computers and Geotechnics,2011,38(1):30-39. [20] PUCKER T,GRABE J.Numerical simulation of the installation process of full displacement piles[J].Computers and Geotechnics,2012,45:93-106. [21] Dassault Systemes.ABAQUS,Version 6.10 documentation[S].2010. [22] DNV.Design and installation of fluke anchors in clay[S].2000. [23] DEGENKAMP G,DUTTA A.Soil resistances to embedded anchor chain in soft clay[J].Journal of Geotechnical Engineering,1989,115(10):1420-1438. [24] VIVATRAT V,VALENT P J,PONTERIO A A.The influence of chain friction on anchor pile design[C]//Proceedings of the 14th Offshore Technology Conference.1982:OTC4178. [25] YEN B C,TOFANI G D.Soil resistence to stud link chain[C]//Proceedings of the 16th Offshore Technology Conference.1984:OTC4769. Large deformation finite element analysis on the kinematic behavior of drag anchors in the seabed LI Peidong,LIU Haixiao,ZHAO Yanbing (School of Civil Engineering,Tianjin University,Tianjin 300072,China) P751 A 10.16483/j.issn.1005-9865.2016.02.008 1005-9865(2016)02-0056-08 2015-01-19 天津市应用基础与前沿技术研究计划重点资助项目(14JCZDJC39900);国家自然科学基金资助项目(51179124) 李培冬(1990-),男,福建漳平人,硕士研究生,从事海洋工程系泊基础数值研究。E-mail:zplpd@163.com 刘海笑。E-mail:liuhx@tju.edu.cn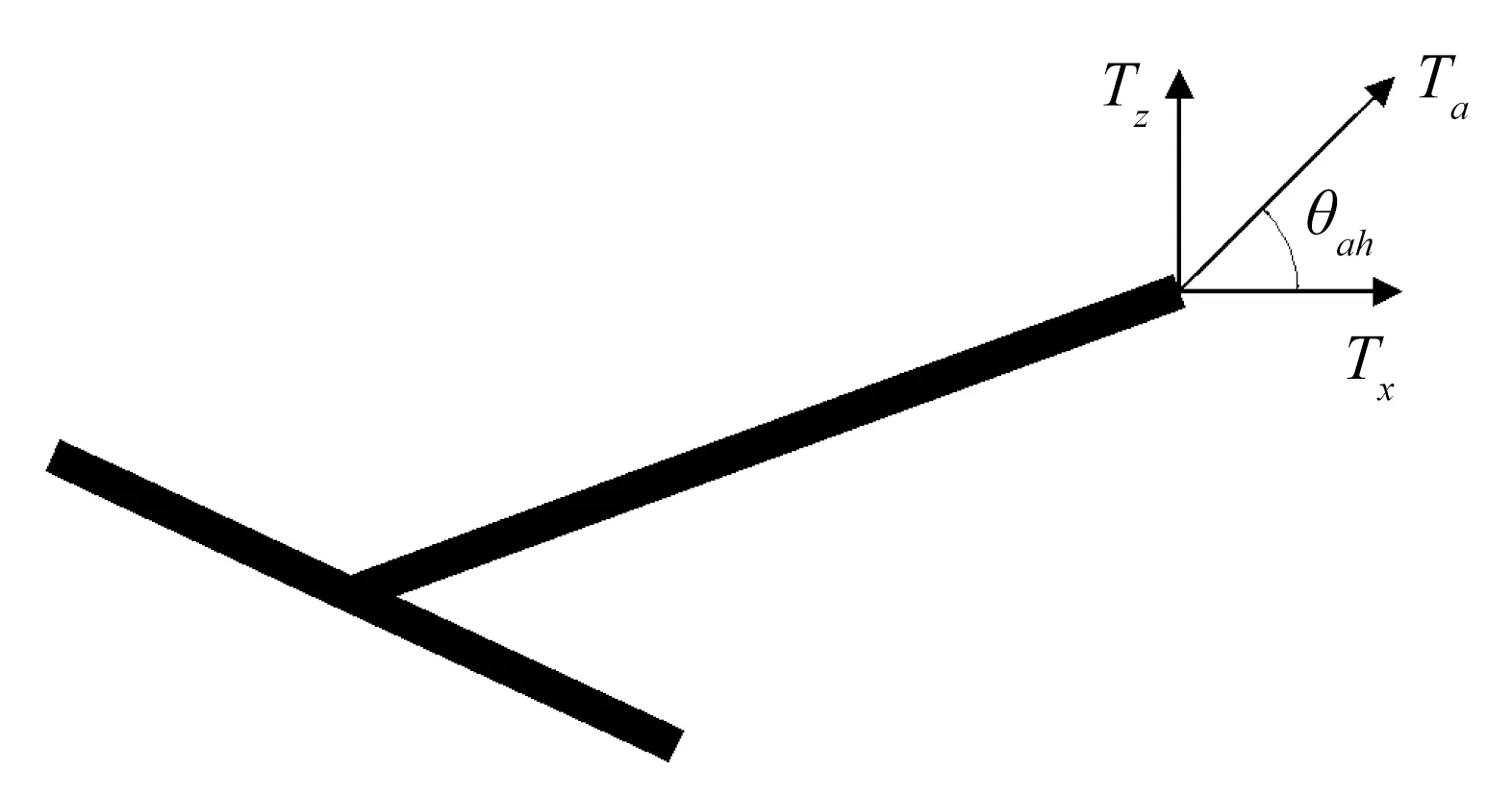
3 数值方法验证




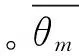
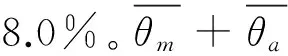
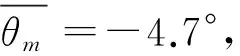

4 结 语

