多桩锥体海洋平台结构冰荷载遮蔽效应离散元分析
王帅霖,狄少丞,季顺迎
(大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023)
多桩锥体海洋平台结构冰荷载遮蔽效应离散元分析
王帅霖,狄少丞,季顺迎
(大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116023)
在海冰与多桩锥体海洋平台结构的相互作用中,平台结构总冰力在海冰流向和桩腿方位的影响下呈现出显著的遮蔽效应。采用具有粘结-破碎效应的离散元方法,基于GPU并行的高性能计算,对不同冰向下锥体海洋平台结构的冰荷载进行了数值分析,确定了不同冰向下平台结构各桩腿的冰力衰减系数并分析了总冰力的遮蔽效应。最后,对自由边界影响下多桩平台结构冰荷载遮蔽效应的产生机理进行了讨论。本文工作可为多桩腿平台结构的冰荷载特性、冰激结构振动以及冰区结构设计提供参考。
多桩锥体海洋平台;离散元方法;GPU并行计算;冰荷载;遮蔽效应
Abstract:During the interaction between sea ice and multi-leg conical offshore platform structure,the global ice load has obvious shadowing effect under the influence of ice drifting direction and pile orientation.In this study,the discrete element method (DEM) with bonding-breaking effect is developed to simulate the ice load on multi-leg conical structure with GPU-based parallel computational technique.The attenuation coefficient of ice load on each pile is determined to analyze the shadowing effect of global ice load in various ice drifting directions.Finally,the mechanism of shadowing effect of global ice load on multi-leg platform is discussed considering the effect of free boundary.This work can be of benefit to the analysis of ice load on multi-leg platform,ice-induced vibration of offshore structure and the design of structure in ice field.
Keywords:multi-legged conical offshore platform; discrete element method; GPU-based parallel computation; ice load,shadowing effect
多桩锥体海洋平台结构广泛地应用于寒区海域的油气开发中,可有效降低冰荷载、改变冰力周期进而避免直立腿平台结构的稳态振动现象[1-3]。在海冰与多桩海洋平台的相互作用过程中,海冰在不同流向下对各个桩腿上的冰荷载作用有很大的差异,呈现显著的多桩结构的冰力遮蔽效应[4-6]。虽然对多桩结构的冰力遮蔽效应开展了一系列的试验研究,但建立通用的冰力遮蔽效应计算方法还需要进一步揭示冰荷载遮蔽效应的产生机理,仍是目前寒区海洋工程结构冰荷载研究的难点[7-9]。
对于多桩腿平台结构的遮蔽效应,Kato和Kato,et al最早通过模型试验分别确定了直立腿和锥体平台在不同冰向下的遮蔽系数[10-11]。Timco,et al在对渤海JZ20-2油气作业区的四桩腿结构设计中开展了相应的模型试验以分析冰荷载的遮蔽效应[12]。最近,黄焱等通过模型试验确定了冰向分别为0°和45°时四桩锥体结构的总冰力和冰激振动,发现冰向在45°时结构存在明显的扭转变形[8-9]。采用有限差分等数值方法也可对多桩结构的冰荷载特性及扭转作用进行分析,并初步得到了与ISO规范较一致的计算结果[7,13-14]。此外,在渤海海冰的现场监测和模型试验中也一直尝试对多桩平台结构的冰力特性和遮蔽效应进行确定[15-17]。以上研究为分析多桩结构的总冰力的遮蔽效应提供了有益的借鉴作用。
在海冰与海洋结构的相互作用研究中,离散单元法可有效模拟海冰由连续体向散体转化的破坏过程,合理反映不同类型海洋结构的冰荷载特性[18-21]。在海冰材料的离散元构造中,可采用球体[19-21]、多面体[18,22-23]或扩展圆盘单元[24]。对于平整冰可采用具有粘接-破碎性能球体单元进行构造,其具有物理意义明确、接触计算简单、接触判断快速等优点,在海冰与结构物相互作用的计算中有很大的优势。由于海冰强度与温度、盐度、加载速率、冰晶结构等诸多因素密切相关,因此在海冰离散元模型中应考虑以上因素影响下的破碎准则[19]。此外,为提高离散元方法的计算规模和效率,可发展基于GPU并行的计算技术,其已有效应用于海洋平台结构的冰荷载数值模拟中[20]。
为此,针对海冰与多桩锥体海洋平台结构的相互作用过程,采用具有粘接-破碎准则的离散元模型,对不同冰向下各桩的冰力遮蔽效应进行数值分析,并对其内在机理进行了讨论。
1 多桩锥体结构冰荷载的离散元模型
1.1海冰离散单元模型
在海冰与海洋结构相互作用的离散元计算中,采用粘接颗粒模型进行海冰材料的离散元构造。每个粘接颗粒单元间具有一定的粘结强度以传递单元间的作用力和力矩。粘接单元间的最大拉应力和剪应力可依据梁的拉伸、扭转和弯曲理论按下式计算[19,25]:

图1 海冰的离散元构造Fig.1 Construction of discrete element of sea ice
粘接颗粒之间的破坏模式采用线性软化模型以有效避免颗粒破坏时将能量全部转化为动能。该线性软化失效准则如图2所示,其可表述为[20,26]
式中:Knf为法向弹性损伤模量;ω为损伤量,当ω=0时,粘接颗粒单元间无破损;当ω=1时,粘接颗粒单元完全断开;当0<ω<1时,粘接颗粒单元间有一定的损伤度,其写作
式中:φ(un)为法向相对位移un的函数,即
式中:nb为法向拉伸强度。

图2 粘结颗粒单元破坏的线性软化损伤模型Fig.2 Linear softening damage model of bonded spherical elements
1.2四桩锥体海洋平台结构离散元计算
渤海JZ20-2平台群由3个四桩腿平台结构组成,如图3(a)所示。依据该平台结构特性,这里构造一个4桩锥体平台结构,其锥体结构如图3(b)所示,各桩腿的间距为20 m。在海冰与平台结构的相互作用模拟中,构造一个60 m×40 m的平整冰,其两侧在竖直方向采用弹性约束以模拟远场冰的作用,如图4所示。考虑海洋平台结构在整体上具有良好刚性,将其设为具有一定质量和阻尼特性的质量单元,由此可对其在海冰作用下的冰振响应进行计算。

图3 渤海JZ20-2 MUQ四桩腿锥体平台及锥体结构参数Fig.3 Four-leg conical platform JZ20-2 in the Bohai Sea and parameters of conical structure
为分析海冰在不同流动方向下与该四桩锥体结构相互作用,分别设定冰向θ=0°、5°、10°、15°、20°、25°、30°、35°、40°和45°,共计10组工况,主要计算参数列于表1。由于海冰的力学性能十分复杂,考虑海冰温度和盐度的影响,并参考海冰单轴压缩和弯曲强度的宏观力学性质试验对海冰单元间的细观参数进行了确定[19-21]。各桩的编号如图4所示,在冰向θ=0°、15°、30°和45°时,计算得到的海冰与平台结构作用情况如图5所示。由于海冰受前侧桩腿的切割破碎作用会形成明显的水道,并会对后侧桩腿的冰力产生遮蔽影响,在不同流向下海冰与桩腿作用后形成的水道结构有很大的差异。当冰向θ=0°时(图5(a)),后侧两个桩腿正好处于前侧桩腿形成的水道内,只会有碎冰块对桩腿作用,其冰力较小;当冰向θ=15°时(图5(b)),后侧桩腿的一部分处于水道内,并受自由边界的影响,其冰荷载也要明显降低;当冰向θ=30°时(图5(c)),3#桩腿受1#桩腿的影响较大;当冰向θ=45°时(图5(d)),3#桩腿则完全处于1#桩腿的水道内。海冰与窄锥结构作用时可发生环向或径向断裂。图6为离散元模拟的海冰径向破坏模式,其与海冰的现场监测现象相一致。

图4 海冰与四桩腿锥体结构相互作用示意Fig.4 Sketch of interaction between sea ice and four-leg conical platform structure
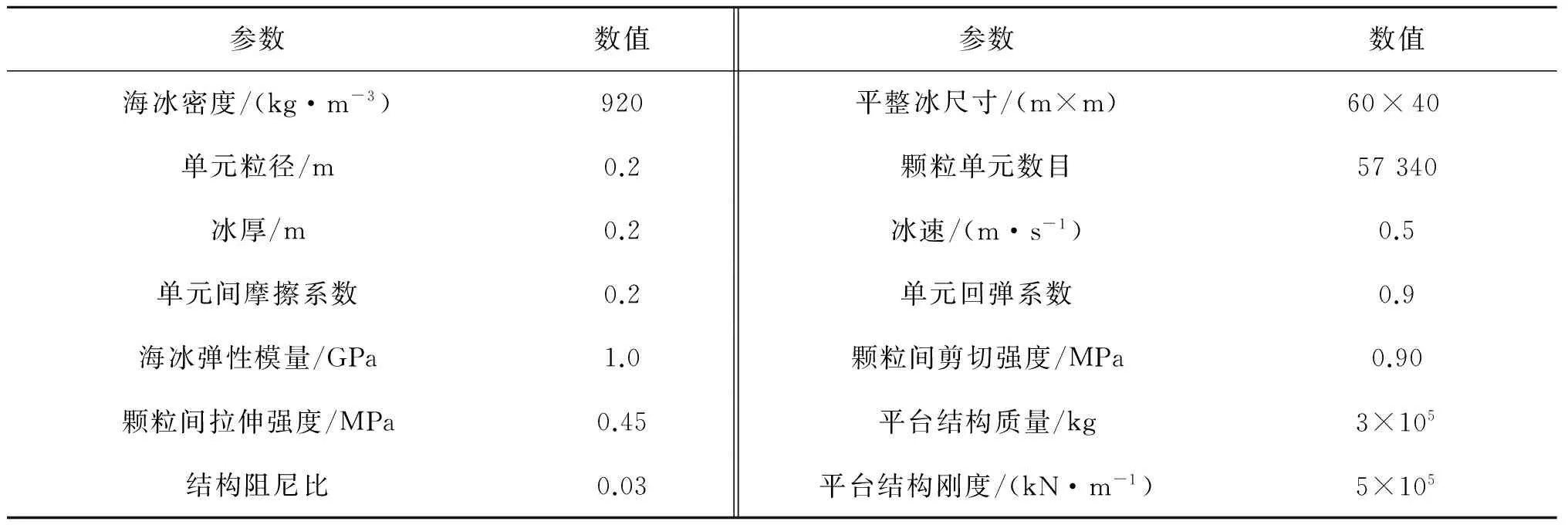
表1 冰荷载离散元模拟的主要计算参数Tab.1 Major computational parameters in DEM simulation of ice load

图5 离散元模拟的不同海冰流向下海冰与四桩腿锥体结构相互作用Fig.5 The interaction between sea ice and four-leg conical structure simulated with DEM in different ice flows

图6 海冰与结构相互作用模拟与现场实测对比Fig.6 Comparison of simulation and field measurement of the interaction between sea ice and structure
为分析平台各桩腿在遮蔽效应下的受力情况,这里以θ=15°为例,各桩腿的冰力时程如图7所示。可以发现各桩腿冰力均呈现出具有很强随机性的脉冲荷载,这与海冰现场监测和室内模型试验结果相一致[2,27-28]。为减小桩腿冰力对比的随机性,这里将各冰力时程中各脉冲荷载的幅值进行提取,并对其平均值进行对比分析[1]。在θ=15°时,该四桩锥体结构上各桩冰力峰值的均值依次为18.9、11.4、11.1和17.3 kN。由此对不同冰向下各桩腿上的冰力时程进行计算,并进一步得到相应的峰值均值如图8所示。可以发现,1#和4#桩一直最先接触到海冰,其不受遮蔽效应的影响,其冰力在不同冰向下相对稳定;2#桩在由θ=0°时的完全遮蔽向θ=45°时的无遮蔽转变,其冰力随冰向的增加而不断增加;3#桩在θ=0°和θ=45°左右时分别由1#和4#桩完全遮蔽,其冰力基本为0,而在θ=25°时受到的遮蔽影响最小,因此其冰力随冰向的增加呈现先增加再减小的趋势,并在冰向为θ=25°时有最大值。
由此可见,各桩上的冰力变化趋势基本由各桩的遮蔽效应所决定。当平台结构的桩腿数目和空间排布发生变化时,各桩腿的遮蔽特性也将随冰向的变化而改变,并可进一步影响到各桩乃至平台结构总冰力的分布特性。
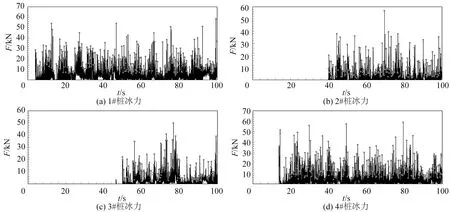
图7 冰向θ=15°时各桩冰力时程Fig.7 Time series of ice loads on each pile at the ice drifting direction θ=15°
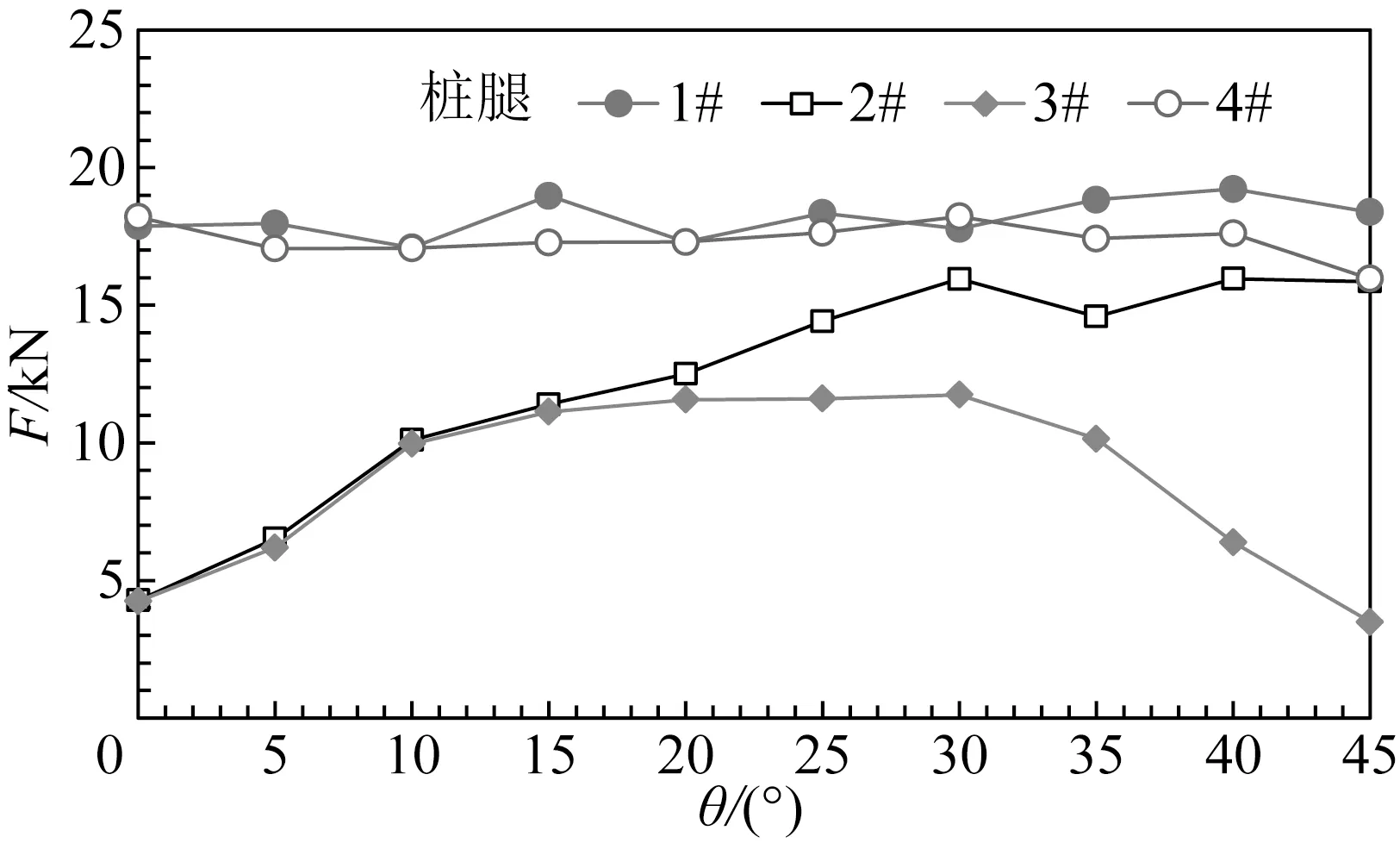
图8 不同冰向下各桩腿冰力峰值Fig.8 The averaged force peak of each pile in various ice drifting directions
1.3多桩锥体结构中单桩冰力的衰减
借鉴Kato建立的多桩结构中单桩冰力的衰减表述方式[10-11],即
式中:F为多桩结构中的单桩冰力,F0为独立桩上的冰力,ks为多桩结构中单桩的衰减系数。
为确定F0值,这里采用表1中的计算参数,并在图4所示计算域内设置一个独立桩腿以消除多桩结构对冰力的遮蔽效应,计算得到F0=22.5 kN。由此,对该平台结构各桩在不同冰向下的衰减系数进行计算,结果如图9所示,其变化规律与各桩冰力是一致的。这主要由不同冰向下各桩腿间的遮蔽影响所决定。由于海冰与平台结构作用过程受各桩间的相互影响,1#和4#桩的冰力也有一定的衰减,为独立桩冰力的80%左右。黄焱等通过室内实验测得冰向为0°和45°时多桩腿结构各腿的冰载荷,其中0°时两迎冰腿的荷载大小相近且小于独立桩腿上的荷载,45°时三个迎冰腿的荷载,经过比较发现两侧桩腿的荷载大小相近且小于前方桩腿[8-9]。这与本文采用离散元方法计算的冰荷载遮蔽效应的变化规律是一致的。
图9 海冰漂移方向影响下各桩腿冰力遮蔽衰减系数Fig.9 The ice force attenuation coefficient of each leg under the influence of ice drifting direction
2 多桩锥体结构冰荷载遮蔽效应
2.1自由边界对单桩冰力的影响

图10 自由边界影响下单桩的冰荷载分析Fig.10 Analysis of ice load on a single pile under the influence of free boundary
多桩平台结构的冰荷载遮蔽效应主要与桩腿所处的海冰条件及其与自由边界的距离密切相关。为分析自由边界对单桩冰荷载的影响,这里对不同边界条件下的单桩锥体冰荷载进行离散元分析。如图10所示,在一个B=30 m,L=50 m的冰区中,自由边界上的颗粒单元在各方向均无约束;冰区约束边界上的颗粒单元在竖直方向有一定约束,在冰流动x方向有速度Vi=0.5 m/s,在y方向为刚性约束。水线处锥体直径D=3.9 m,其结构如图4(b)所示;桩柱内侧至自由边界的距离设为s。这里取用表1中的计算参数,并改变桩柱位置对单桩的冰力时程进行了离散元分析。由此得到的冰力峰值平均值如图11(a)所示。可以发现,冰力随桩柱到自由边界距离s的增加而增加,并趋于稳定,且有F0=24.58 kN。
定义无量纲距离s*=s/D,由式(5)可得不同自由边界距离处桩柱的衰减系数,如图11(b)所示。由此可以发现,该衰减系数可以分为两段,即

图11 自由边界对结构冰载荷及其衰减系数的影响Fig.11 Free boundary impact on the structure of ice loads
2.2多桩锥体结构冰力遮蔽效应
在多桩平台结构的总冰力计算中,需同时考虑海冰的非同时破坏、遮蔽效应、海冰堆积等因素,其总冰力为[29]
式中:FT为多桩结构的总冰力,FA为多个独立桩受到的总冰力,Ks为遮蔽系数,Kn是考虑非同时破坏的因素,一般选为0.9,Kj考虑冰堆积的因素,对于平整冰Kj=1.0。遮蔽系数Ks是每个桩腿遮蔽影响的共同效应,其与桩腿排布结构、冰向、桩径等因素有关,需针对所研究海洋平台的结构特性进行确定。
针对本文的四桩锥体平台结构,对各个桩腿的遮蔽效应进行分析。图12为不同冰向下,1#桩和4#桩对海冰切割后形成水道的示意图。该水道形成了对2#桩和3#桩的自由边界。图中各几何参数有以下关系:
桩腿间距离L=B=20 m。桩腿对海冰切割后形成的水道宽度由离散元计算获得。由图5计算结果,取w=D/4。由此,2#桩和3#桩距离自由边界的无量纲距离分别为
式中:s21为2#桩腿到1#桩所形成水道边界的距离,s31、s43为3#桩分别到1#桩和4#桩所形成水道边界的距离。
采用式(6)、(8)和(9)对图12中2#和3#桩的冰力衰减系数进行计算,由此得到的两桩腿的冰力衰减系数如图13所示,图中给出了离散元结果与式(6)计算结果的对比情况。可以看出它们得到的冰力衰减系数在趋势上具有很好的一致性。但在数值上,由式(6)得到的理论解要高于离散元结果。这主要是由于采用式(6)计算冰力衰减时没有考虑冰盖与前部桩腿作用时产生的前期损伤。

图12 桩腿与水道自由边界距离计算Fig.12 Distance calculation of pile to free boundary of water channel
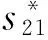
将不同冰向下的参数代入上式,并依据基于ISO标准的式(7)可得到该四桩锥体平台结构的总冰力遮蔽系数,如图14所示。该图也给出了离散元计算的总冰力遮蔽系数。可以发现ISO计算结果与离散元模拟结果具有很好的一致性。但在ISO计算中未考虑海冰与前侧桩腿作用时产生的前期损伤,其总冰力遮蔽系数要略高于离散元的计算结果。
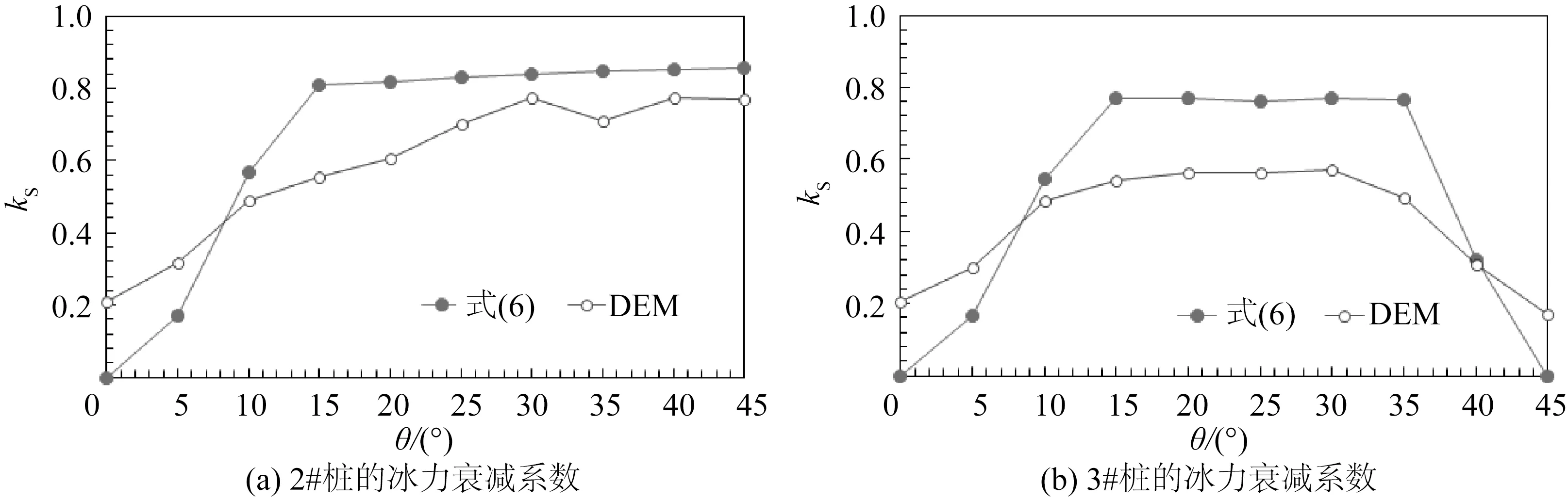
图13 多桩腿结构中遮蔽影响下2#、3#桩的冰力衰减系数Fig.13 Attenuation coefficient of ice load on leg 2 and leg 3 under the shielding effect of multi-leg structure
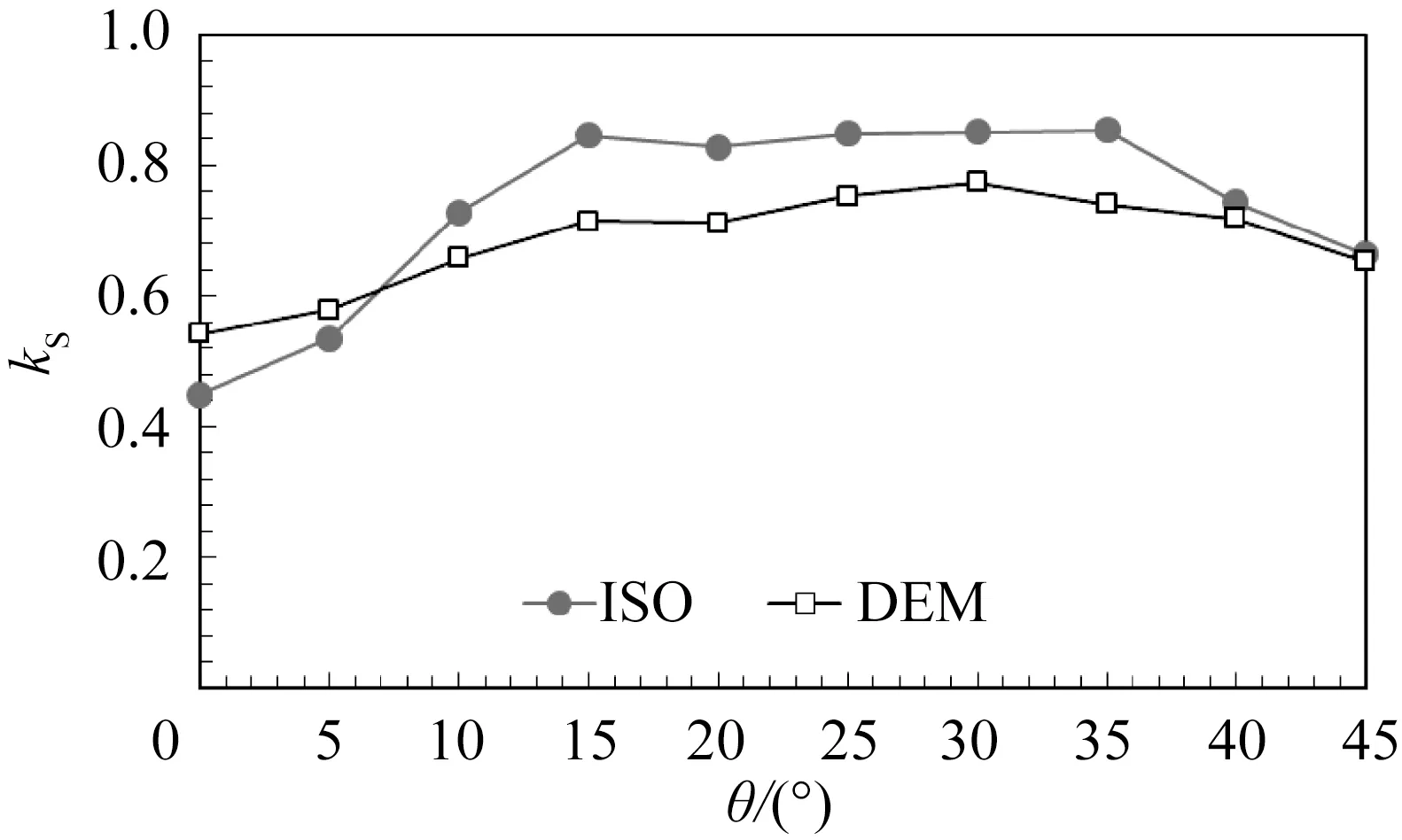
图14 四桩锥体平台结构总冰力遮蔽系数Fig.14 Yielding coefficient of global ice load on four leg conical platform structure
3 结 语
在多桩海洋平台结构总冰力计算中,总冰力的遮蔽效应是影响平台结构设计和抗冰性能分析的重要因素。为分析多桩锥体海洋平台的冰力遮蔽系数,采用离散元方法对不同冰向下各桩腿的动冰力时程进行了数值计算,确定了各桩冰力峰值随冰向的变化规律。为解释冰力遮蔽效应的产生机理,分析了自由边界对单桩冰力的影响,由此确定了无量纲距离与单桩冰力衰减系数的对应关系。依此确定了四桩锥体平台结构总冰力的遮蔽系数,其变化规律与ISO标准相一致。在冰力遮蔽系数确定中还应进一步考虑冰内前期损伤的影响,同时进一步考虑海冰材料性质与温度、盐度、加载速率等因素的关系,发展适于用合理描述海冰宏观力学行为的离散元方法,以更合理地确定多桩平台结构的总冰力。通过对四桩锥体平台结构总冰力遮蔽效应的数值分析,为不同桩腿数量和排布形式下多桩海洋平台结构的总冰力分析提供了有益的思路。
[1] QU Y,YUE Q,BI X,et al.A random ice force model for narrow conical structures[J].Cold Regions Science and Technology,2006,45:148-157.
[2] TIAN Y,HUANG Y.The dynamic ice loads on conical structures[J].Ocean Engineering,2013,59:37-46.
[3] PAAVILAINEN J,TUHKURI J.Pressure distributions and force chains during simulated ice rubbling against sloped structures[J].Cold Regions Science and Technology,2013,85:157-174.
[4] SHI Q,HUANG Y,SONG A,et al.Non-simultaneous failure of ice in front of multi-leg structures[J].China Ocean Engineering,2002,16 (2):183-192.
[5] 季顺迎,王安良,车啸飞,等.锥体导管架海洋平台冰激结构振动响应分析[J].海洋工程,2011,29(2):33-39.(JI Shunying,WANG Anliang,CHE Xiaofei,et al.Analysis of ice induced structure vibration of offshore jacket platform with ice breaking cone[J].The Ocean Engineering,2011,29(2):33-39.(in Chinese))
[6] KARULIN E,KARULINA M.Peculiarities of multi-legged platform operation in ice condition[C]//Proceeding of the ASME 33rd International Conference on Ocean,Offshore and Arctic Engineering.San Francisco,California,USA.2014:OMAE2014-23203.
[7] KARULINA M M,SHKHINEK K N,THOMAS G A N.Theoretical and experimental investigations of level ice interaction with four-legged structures[C]//Proceedings of the 21st International Conference on Port and Ocean Engineering under Arctic Conditions.Montréal,Canada.2011:POAC11-032.
[8] HUANG Y,MA J,TIAN Y.Model tests of four-legged jacket platforms in ice:Part 1.Model tests and results[J].Cold Regions Science and Technology,2013,95:74-85.
[9] HUANG Y,YU M,TIAN Y.Model tests of four-legged jacket platforms in ice:Part 2.analyses and discussions[J].Cold Regions Science and Technology,2013,95:86-101.
[10] KATO K.Total ice force on multi legged structures[C]//Proceedings of 10th International Symposium on Ice.Espoo,Finland.1990,2:974-983.
[11] KATO K,ADACHI M,KISHIMOTO H,et al.Model experiments for ice forces on multi conical legged structures[C]//Proceedings of the 4th ISOPE Conference.Osaka,Japan.1994,2:526-534.
[12] TIMCO G W,IRANI M B,TSENG J,et al.Model tests of dynamic ice loading on the Chinese JZ-20-2 jacket platform[J].Canadian Journal of Civil Engineering,1992,19:819-832.
[13] YAZAROV S M,SHARAPOV D.Ice torsion moments on four leg structure[C]//Proceedings of the 20th International Conference on Port and Ocean Engineering under Arctic Conditions.Lulea,Sweden.2009:POAC09-132.
[14] SHKHINEK K N,JILENKOV A G,BLANCHET D,et al.Ice loads on a four leg structure[C]//Proceedings of the 20th International Conference on Port and Ocean Engineering under Arctic Conditions.Lulea,Sweden.2009:POAC09-43.
[15] YUE Q,QU Y,BI X,et al.Ice force spectrum on narrow conical structures[J].Cold Regions Science and Technology,2007,49:161-169.
[16] 张树德,孙振平.基于模型冰试验的多腿柱导管架平台结构最大冰载荷计算新方法——以渤海绥中36-1油田A II井口平台为例[J].中国海上油气,2014,26(S1):17-20.(ZHANG Shude,SUN Zhenping.New calculation method for the maximum ice load on multi-leg jacket based on ice model test result:case of SZ36-1 oil field WHP-A II in Bohai Sea[J].China Offshore Oil and Gas,2014,26(S1):17-19.(in Chinese))
[17] 许宁,岳前进,王延林.基于水下光纤应变监测的导管架结构总冰力测量方法[J].海洋工程,2014,32(5):9-14.(XU Ning,YUE Qianjin,WANG Yanlin.Ice load measurement based on underwater fiber strain monitoring of jacket structure[J].The Ocean Engineering,2014,32(5):9-14.(in Chinese))
[18] POLOJäRVI A,TUHKURI J.On modeling cohesive ridge keel punch through tests with a combined finite-discrete element method[J].Cold Regions Science and Technology,2013,85:191-205.
[19] 季顺迎,狄少丞,李正,等.海冰与直立结构相互作用的离散单元数值模拟[J].工程力学,2013,30(1):463-469.(JI Shunying,DI Shaocheng,LI Zheng,et al.Discrete element modelling of interaction between sea ice and vertical offshore structures[J].Engineering Mechanics,2013,30(1):463-469.(in Chinese))
[20] 狄少丞,季顺迎.海冰与自升式海洋平台相互作用GPU离散元模拟[J].力学学报,2014,46(4):562-571.( DI Shaocheng,JI Shunying.Gpu-based discrete element modeling of interaction between sea ice and jack-up platform structure[J].Chinese Journal of Theoretical and Applied Mechanics,2014,46(4):562-571.(in Chinese))
[21] JI Shunying,LI Zheng,LIU Shewen.Discrete element simulation of sea ice flexural strength[C]//Proceedings of 21st IAHR International Symposium on Ice.Dalian,China.2012.
[22] LAU M,LAWRENCE K P,ROTHENBURG L.Discrete element analysis of ice loads on ships and structures[J].Ships and Offshore Structures,2011,6(3):211-221.
[23] SELVADURAI A P S,SEPEHR K.Two-dimensional discrete element simulations of ice-structure interaction[J].International Journal of Solids and Structures,1999,36:4919-4940.
[24] SUN S,SHEN H H.Simulation of pancake ice load on a circular cylinder in a wave and current field[J].Cold Regions Science and Technology,2012,78:31-39.
[25] POTYONDY D O,CUNDALL P A.A bonded-particle model for rock[J].International Journal of Rock Mechanics & Mining Sciences,2004,41:1329-1364.
[26] PAAVILAINEN J,TUHKURI J,POLOJARVI A.2D numerical simulations of ice rubble formation process against an inclined structure[J].Cold Regions Science and Technology,2011,68:20-34.
[27] 岳前进,毕祥军,于晓,等.锥体结构的冰激振动与冰力函数[J].土木工程学报,2003,36(2):17-19.(YUE Qianjin,BI Xiangjun,YU Xiao,et al.Ice-induced vibration and ice force function of conical structure[J].China Civil Engineering Journal,2003,36(2):17-19.(in Chinese))
[28] 曲月霞,李广伟,李志军,等.正倒锥体结构上冰力谱分析实验研究[J].海洋工程,2001,19(3):38-42.(QU Yuexia,LI Guangwei,LI Zhijun,et al.Analysis of ice force spectrum in physical experiments[J].The Ocean Engineering,2001,19(3):38-42.(in Chinese))
[29] ISO 19906:2010 Petroleum and natural gas industries-Arctic offshore structures[S].International Organization for Standardization,2010.
Discrete element analysis of shadowing effect of ice load on multi-leg conical offshore platform structure
WANG Shuailin,DI Shaocheng,JI Shunying
(State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China)
P731.15
A
10.16483/j.issn.1005-9865.2016.02.001
1005-9865(2016)02-0001-09
2015-01-29
国家自然科学基金资助项目(41176012);国家海洋公益性行业科研专项经费资助项目(201105016,201205007);高等学校博士学科点专项科研基金资助项目(20130041110010)
王帅霖(1990-),男,辽宁鞍山人,博士研究生,主要从事寒区海洋工程研究。E-mail:wangshuailin@mail.dlut.edu.cn
季顺迎。E-mail:jisy@dlut.edu.cn

