海岸破碎带植物消浪数值模拟研究

刘 达，黄本胜，邱 静，谭 超

(1.广东省水利水电科学研究院 广东省水动力学应用研究重点实验室，广东 广州 510610; 2.河口水利技术国家地方联合工程实验室，广东 广州 510610)

海岸破碎带植物消浪数值模拟研究

刘 达1，2，黄本胜1，2，邱 静1，2，谭 超1，2

(1.广东省水利水电科学研究院 广东省水动力学应用研究重点实验室，广东 广州 510610; 2.河口水利技术国家地方联合工程实验室，广东 广州 510610)

沿海防浪林能形成柔性的植物消浪体系，可以有效降低风暴潮灾害。由于防浪林消浪效果受波浪、近岸水深及植物等多重因素的影响，消浪机理较为复杂，以往的系统研究成果较少。本文以立面二维自由面紊流模型为工具，建立了基于植物冠层特征的多孔介质模型，精细地模拟了破碎波对植物带的冲击，并与物理模型试验结果进行了对比验证，计算分析了植物带宽度、植物密度、滩地水深等因素对消浪效果的影响。

植物消浪；消浪系数；植物带宽度；植物密度；波浪条件；数学模型

Abstract:Wave-proof plants along sea walls can effectively counteract the damage caused by ocean disasters like storm surges and typhoon waves.However,most current researches merely focus on the wave dissipation rate,and concern little about vegetation natures such as plant width,density and height,or hydrodynamic characteristics like wave conditions and water depth.Therefore,this work was conducted to make up for this scarcity.Based on two-dimensional swirl models,a porous media model was established to simulate wave propagation into the vegetated area under circumstances of different vegetation parameters and water depths.Meanwhile,the principle of wave breaking in the eco-hydraulic system was also investigated.

Keywords:biological wave counteracting; counter-wave coefficient; width of counter-wave system; density of counter-wave system; depth of water; numerical simulation

华南沿海地区是我国经济高度发达地区，特殊的地理位置使得该地区频繁遭遇台风暴潮的袭击，每年沿海台风暴潮的袭击给该地区带来巨大的损失。在长期的生产实践中，人们逐步认识到在海堤外滩种植生物防浪林，能够形成柔性的植物消浪体系，使波浪在到达堤前得到最大程度的消减，降低波浪的冲击力及爬高，减轻对海堤的危害。

鉴于防浪林对于海岸防护的重要作用，国内外均开展了植物消浪的相关研究，主要研究手段是物理模型和数学模型。在物理模型研究上，黄本胜、吉红香等[1-2]通过概化模型试验，研究了珠江三角洲内河堤的植物消浪问题。白玉川等[3]用裁减的桧柏枝模拟防浪树，研究了非破碎波条件下的防浪林消浪效果。Knutson,et al[4]和Möller and Spencer[5]研究发现波高在植物区内是呈指数级衰减的。Muslesh and Cruise[6]采用刚性杆模拟刚性未淹没植物，研究了植物杆径与横纵排列对水深及流速的影响。在数模研究上，林鹏智、Chen等[7-9]将植物区作刚性圆柱群假设，开发了紊流三维植物模型及刚性植物区紊流浅水模型。Righetti and Armanini[10]研究了完全淹没的浓密灌木中的水流阻力，建立了基于时间和空间平均的数学模型。Harada和Imamura[11]数值模拟了非破碎波条件下不同树林宽度、密度等条件下防浪林对波浪消减的作用。

与物理模型试验方法相比，数值模拟方法在植物消浪的研究上具有其自身的优势，可以显示各时刻的精细流场及波浪破碎冲击过程，且植物带的宽度、密度及波浪条件等计算组合可以更加丰富，可以支撑植物消浪这种复杂水动力学问题的研究。本文以立面二维自由面紊流模型为工具，建立了基于植物冠层特征的多孔介质模型，精细地模拟了破碎波对植物带的冲击，并与物理模型试验成果进行了对比验证，应用该模型计算分析了植物带宽度、植物密度、滩地水深、波长等因素对消浪效果的影响。

1 植物波浪数学模型简介

目前国内外植物消浪数模的研究对植物区的概化普遍以刚性圆柱群为基本假设，该假设作为研究波浪在树杆区的传播过程模拟较为精细，但是根据本文物模试验的最新成果，树冠消浪贡献可以占到防浪林整个消浪效果的约70%，然而植物区的圆柱群假设对于树冠的模拟概化却是较为失真的，主要原因是树冠的结构复杂，简单概化为柱状体有所欠缺。此外现有的研究考虑到植物与波浪作用的复杂性，普遍选取非破碎波条件作为研究工况，这与风暴潮时波浪在近岸破碎后冲击防浪林带的实际过程偏离也较大。因此，本研究对植物区概化上抓住树冠消浪的主要矛盾，以立面二维自由面紊流模型为工具，建立了基于植物冠层特征的多孔介质模型。

1.1控制方程

1.1.1 波浪控制方程

1)不可压缩液体的雷诺方程

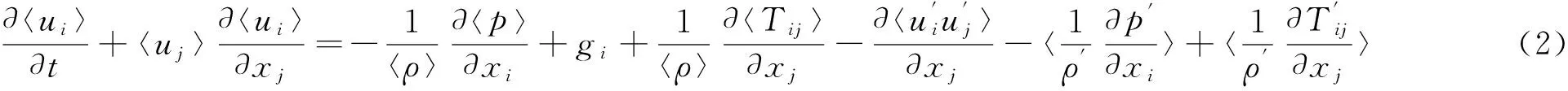
式中：i，j=1，2；ui为i方向的速度分量；gi为i方向的重力加速度；Tij为粘性应力张量；ρ为密度。式中〈〉表示平均量，上标为“’”的量表示紊动量。

2)紊流模型

采用k-ε模型，其中k为紊动动能，ε为紊动耗散率，方程如下：

紊动动能k的传输方程：

式中：σk为斯密特常数，与扩散(而非耗散)有关；vt为涡粘系数。

紊动耗散率ε的输移方程：

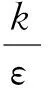
1.1.2 孔隙介质中的流体运动控制方程

式中：n为孔介质中的孔隙率，cA为附加质量系数。

1.2控制方程的离散格式、求解方法及自由面处理方法

本模型采用有限差分法离散求解。将整个计算域离散成m×n的矩形网格，用二步映射法对雷诺方程进行求解。采用VOF法(流体体积法)跟踪自由水面的运动，VOF法对自由水面的具体位置采用几何重建方法来确定，它采用分段线性近似的方法来表示自由水面[12]。

1.3植物区的概化模拟方法

以往的研究一般以圆柱组来假设构建数学模型，主要考虑植物区对水流产生的x方向的拖曳力，这主要是由于在近岸浅水波条件下，x方向的速度远大于y方向的速度，而衰减作用于速度矢之间为二次幂关系，因而y向的阻力效果是忽略的。但在研究实际海堤外防浪林消浪过程时发现，对于近岸破碎波来说，完全忽略y向的阻力效果可能是不够准确的，而且树冠层所发挥的消波消浪作用要比树干层显著。

根据物理模型试验研究成果，在破碎波条件下以红树林为原型的模型树的树冠消浪贡献占到防浪林整个消浪效果约70%。树冠层起到较大消波作用的原因是由于波浪中水质点的运动速率在垂直方向从水面向下递减从而造成上层阻力效果比较明显，对于居于同样垂向位置的树冠层和树干层而言，由于前者具有的细密枝叶可以在不同方向对破碎波的冲击形成有效阻力，且同时会造成很多小尺度的紊动从而导致波能的消耗。

由于连成片的防浪林，其树冠也连为一体，树冠枝叶互相刺入相邻的树冠中，郁闭度接近100%。其树叶多为椭圆形小叶片，十分茂密，防浪林树冠在空间分布上与多孔介质假设的球形体更为相近。同时，在物理模型试验中也观察到，破碎波在滩地上的传播特性与非变形正弦波的传播差异很大。非变形正弦波传播中流体质点做椭圆运动，波浪在水平方向的速度较大；而波浪爬高的破碎过程为陡波峰向前下方以接近45°角冲击入防浪林内(见图1)，因此球形物的各向同性假设也较为适用，因为球形物的阻力能够同时产生x方向和y方向的阻力。

因此，在本次生物消浪的数学模型中，提出一种分区多孔介质的概化模型。即将树冠区和树干区分成两个多孔介质区(见图2)，分别赋予不同的孔隙率等参数(采用量筒排水法测定)。

图1 物理模型破浪破碎后冲击流向示意Fig.1 Schematic diagram of the wave impact process in the physical model test

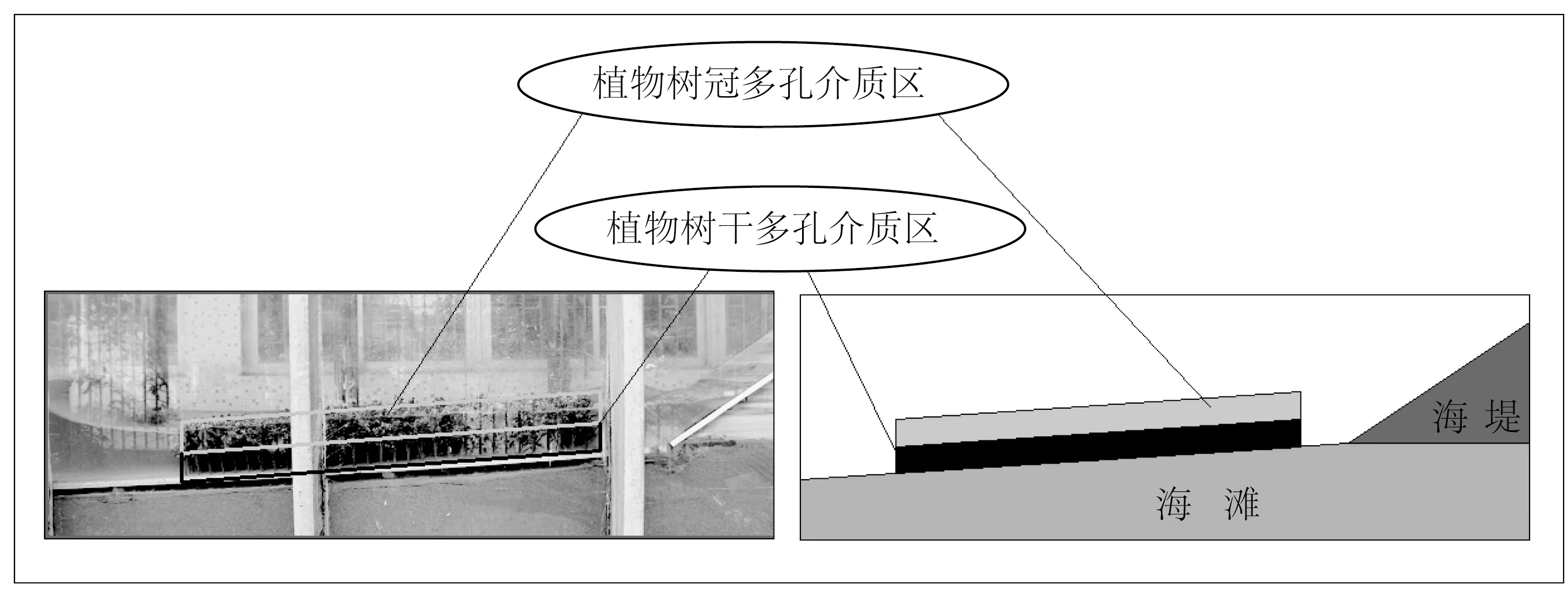
图2 树冠区和树干区多孔介质概化模型示意Fig.2 Schematic diagram of the model of porous media

1.4计算区域及网格划分

在二维波浪数值水槽中建立了基于多孔介质的防浪林数学模型，见图3。计算区域的网格划分在x方向上为四个区(四个分区：x=-20～-10 m、x=-10～-5 m、x=-5～5 m、x=5～10.1 m)、y方向上为三个区(三个分区：y=0～0.1 m、y=0.1～0.7 m、y=0.7～1.3 m)，边界设置为均匀网格，中间是渐变网格。

图3 数学模型计算区域示意Fig.3 Schematic diagram of numerical model calculation area

2 物理模型试验简介

植物消浪的物理模型试验在波浪水槽中进行，模型上安装有波高仪、爬高仪及压力传感器等量测设备。物模的试验布置与数模相同，见图3。依据华南沿海红树林的外型参数及波浪要素的特征值，结合实验室波浪水槽的实际情况，按照重力相似原则确定模型的比尺lr=20。选择了外形特征与原体红树林基本相似的模型树，模型树的外形特征为树高20 cm、胸径0.5 cm、树干高10 cm、冠高10 cm、冠幅5 cm。

3 植物消浪数学模型验证

根据量筒排水法测得的模型树树干和树冠的孔隙率分别为0.84和0.94，多孔介质模型参数d在树干层和树冠层分别给0.2 cm和1 cm。在造波板前水深0.70 m、正弦波波高0.15 m、波周期1.79 s的组次下比较海堤堤脚的最大波压力和瞬间波面线的数学模型计算结果与物理模型试验结果。

海堤堤脚的最大波压力是整个堤身上压力分布最大的位置，该指标也是衡量消浪效果的一个重要参数，两者的比较见图4。由图4可见，总体上与数模计算的时均压力过程线较为接近。

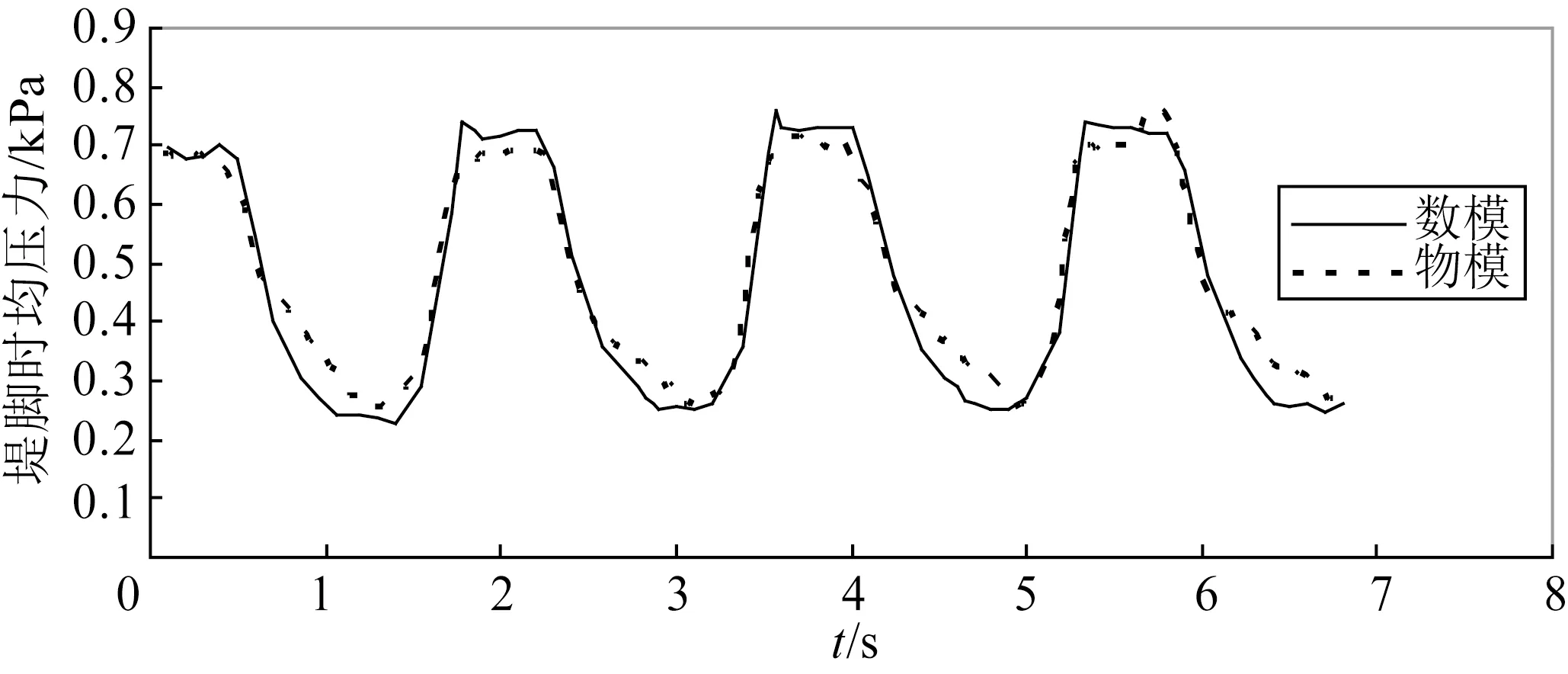
图4 海堤堤脚时均压力过程线比较(防浪林宽度1.0 m)Fig.4 Comparison of the pressure process line at the foot of seawall(forest width:1.0 m)

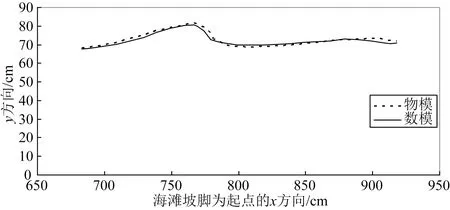
图5 t=0.6 s时瞬时形态及波面线比较Fig.5 Comparison of the wave line and the flow regimes at t=0.6 s moments

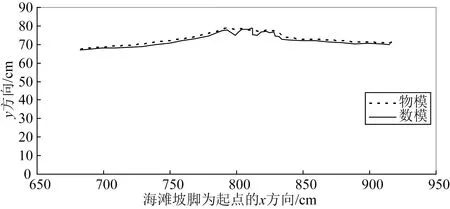
图6 t=0.9 s时瞬时形态及波面线比较Fig.6 Comparison of the wave line and the flow regimes at t=0.9 s moments

图5和图6为破碎波冲击植物带瞬间的波面线物模和数模对比，可见两者吻合较好。

综上，数学模型可以较好地模拟破碎波对植物带的冲击，计算精度满足要求，可以用于后续的模拟计算。

4 数值模拟计算结果分析

破碎波条件下的植物带消浪系数采用波浪爬高值作为指标。消浪系数K的值越大表示消浪效果越好，K表达式如下：

式中：Ha0为无防浪林时的波浪爬高，Ha为有防浪林时的波浪爬高。

4.1无植物区波浪场模拟结果

当造波板前水深0.70 m、正弦波波高0.15 m、波周期1.79 s时，t=0.3、0.6、0.9、1.2 s时刻的无植物区工况各典型时刻的瞬时波面线及速度矢量场见图7。从图中可以看出，波浪传播到近岸以后开始变形，波峰逐渐陡峭，在堤前发生剧烈破碎后冲击了海堤，最大爬高值达0.48 m。

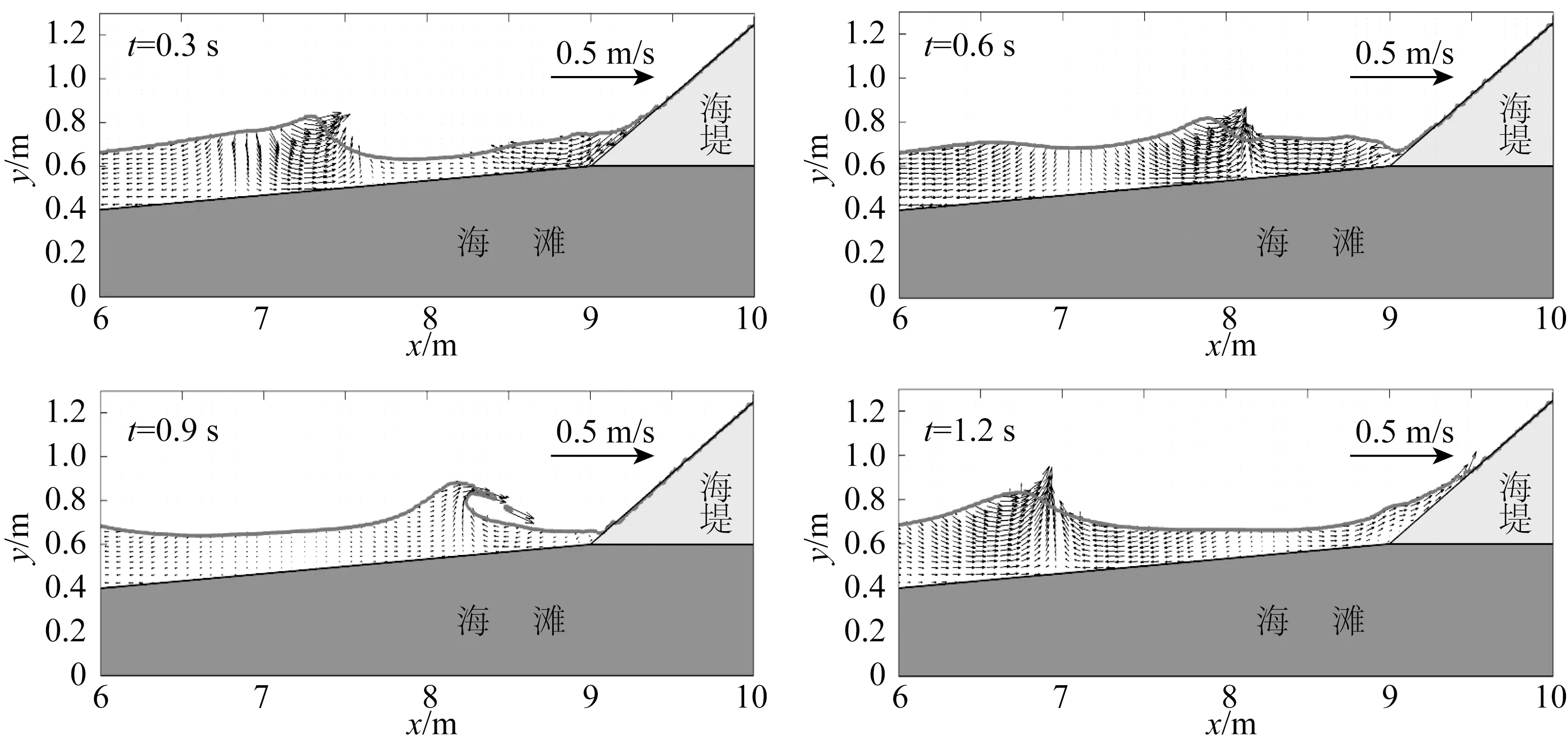
图7 无植物区时，t=0.3、0.6、0.9、1.2 s的速度矢量场Fig.7 Velocity vector field at t=0.3、0.6、0.9、1.2 s without counter-wave plants

4.2植物区宽度对消浪效果的影响

主要的计算工况为防浪林带宽度0.5 m(原体10 m，由于红树林的外形尺寸都是按照原体1∶20的比例进行数模建体，因此数模计算也存在比尺)、1.0 m(原体20 m)、2.0 m(原体40 m)、3.0 m(原体60 m)、4.0 m(原体80 m)、5.0 m(原体100 m)，计算结果见图8、图9。计算结果显示，防浪林带宽度0.5 m(原体10 m) ～1.5 m(原体30 m)区间的消浪系数增长较快，由0.507增加到0.723，当防浪林宽度超过1.5 m(原体30 m)后，消浪系数的增幅明显趋缓。

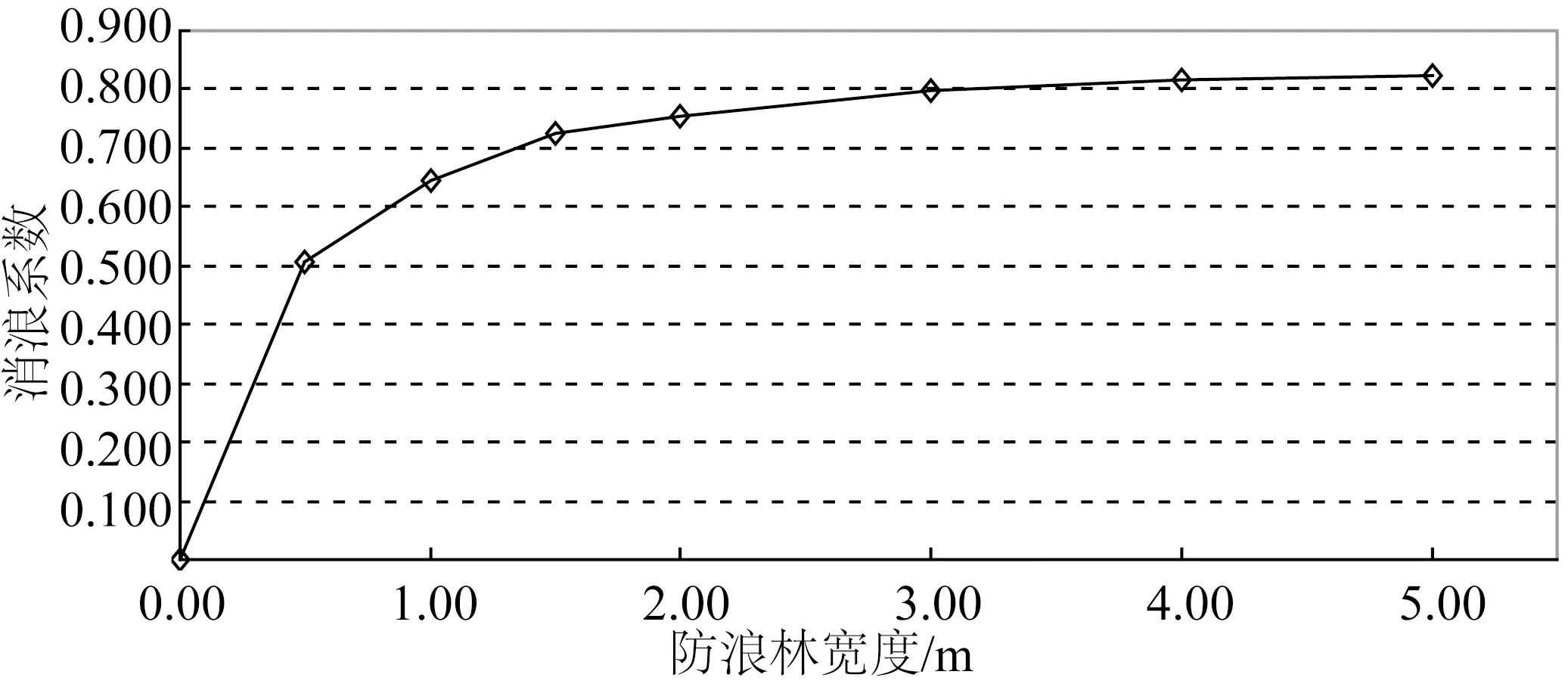
图8 消浪系数随防浪林宽度变化情况Fig.8 Variation of counter-wave coefficient with the width of counter-wave plants

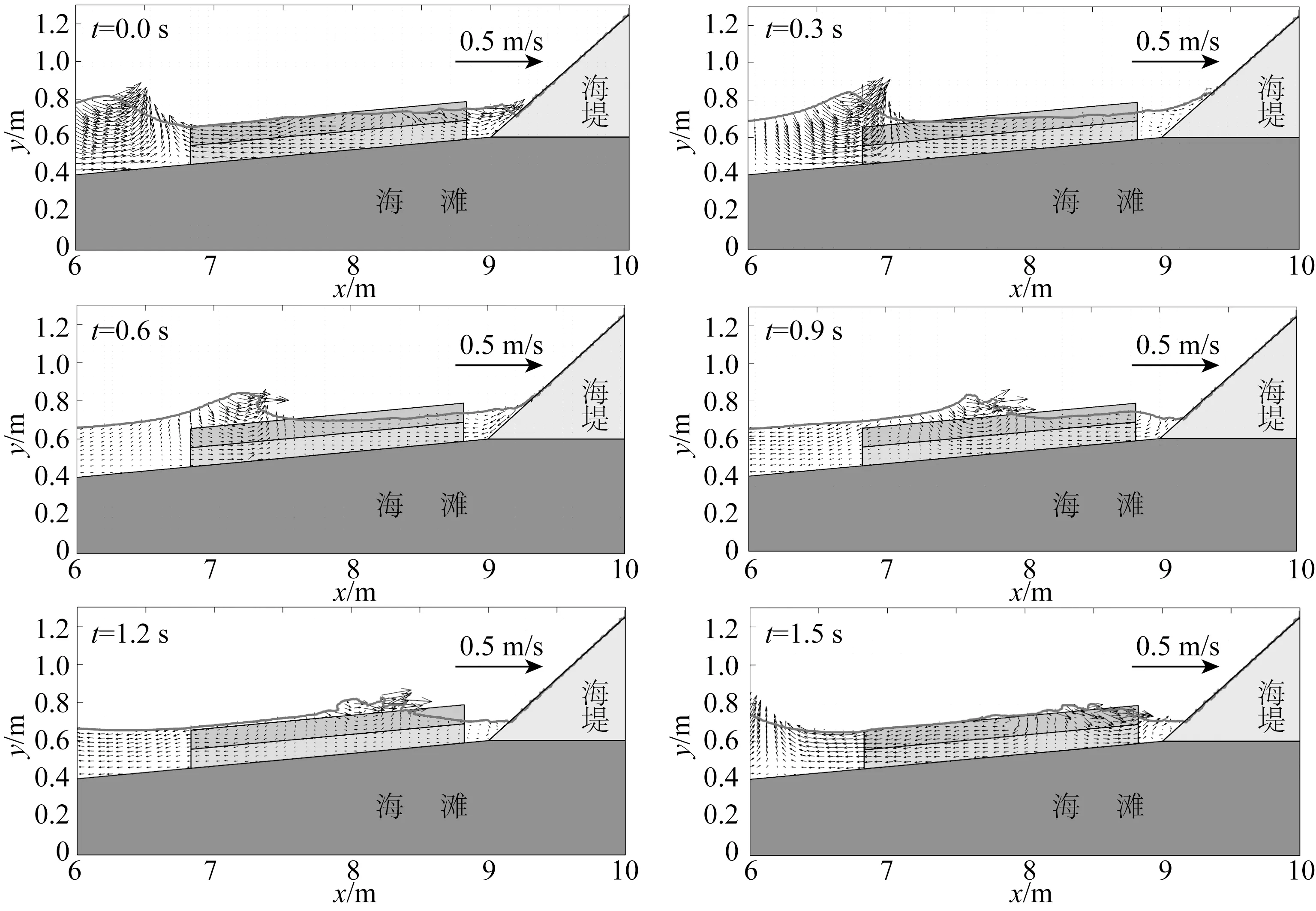
图9 防浪林宽度为2.0 m时，t=0.0、0.3、0.6、0.9、1.2、1.5 s的速度矢量场Fig.9 Velocity vector field at t=0.0、0.3、0.6、0.9、1.2 and t=1.5 s when the width is 2.0 m

4.3植物区生物量对消浪效果的影响

植物区的种植密度对消浪效果产生的影响是显著的。在同样宽度的海滩上种植的防浪林密度不同会产生不同的消浪效果。从营林的角度而言，树林种植的过于密集造成生态营养失调从而会影响防浪林的成活；而如果种植的过于稀疏，则会使其经常遭受风浪乃至台风暴潮的袭击而变得相对脆弱，这样也会大大的降低生态防浪林的成活。计算了防浪林宽度为1.5 m时，树冠孔隙率分别为0.96、0.92、0.84、0.76、0.68、0.60、0.62，相应的树干孔隙率为0.99、0.97、0.94、0.91、0.88、0.85、0.82的各组次工况。由于孔隙率为孔隙介质在整体空间中所占的比例，不能直接反映区内的植物量，故换算成空间内的植物比例，以树冠为例，其植物比例分别为0.04、0.08、0.16、0.24、0.32、0.40、0.48，植物比例的选取系列基本能够覆盖自然界中防浪林可能出现的值，计算结果见图10。

计算结果显示，当滩地1.5 m范围内的植物比例(以树冠区计算)由0增长至0.16时，消浪效果呈快速增长趋势，消浪系数由0迅速增长至0.727，从增加的趋势线可以看出，植物比例0～0.08范围内，消浪系数的增长基本处于线性关系，当植物比例大于0.08时，非线性变化较为明显。当植物比例大于0.16时，消浪系数的增幅明显趋缓，植物比例由0.16增加到0.48，增大了2倍，而消浪系数仅增加了15.7%。由此说明防浪林的种植密度存在一个重要拐点，树冠区植物比例大于0.16(相应孔隙率0.84)以后，消浪效果的增长趋缓。

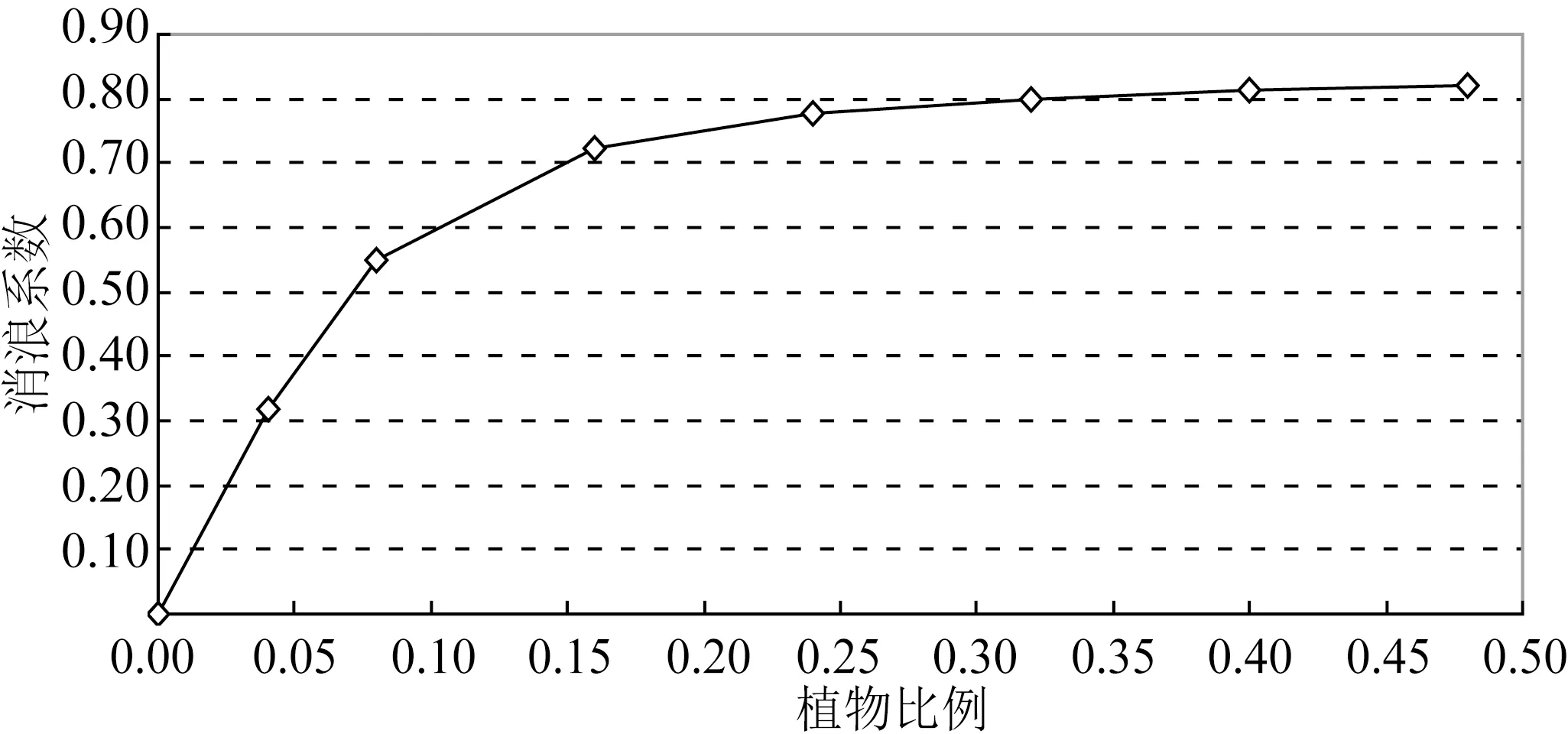
图10 消浪系数随生物量变化情况Fig.10 Variation of counter-wave coefficient with plant biomass

4.4滩地水深对消浪效果的影响

在保持防浪林的树种高度、林带宽度(1.5 m)和种植密度(孔隙率)不变的情况下，波周期和波高分别为1.79 s、15 cm时，计算了造波板前水深分别为0.60、0.65、0.70、0.75、0.80、0.85、0.90 m各组次(见图11)，计算结果见图12。

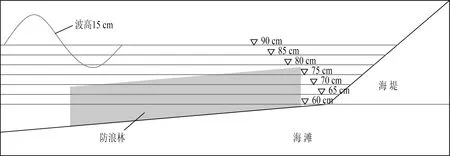
图11 不同滩地水深计算工况示意Fig.11 Schematic diagram of different water depths

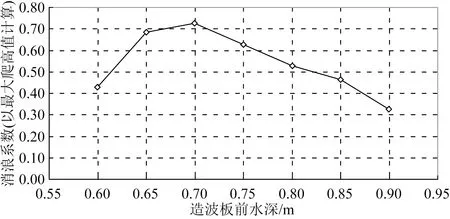
图12 消浪系数随水深的变化规律Fig.12 Variation of counter-wave coefficient with water depth

由图12可见，消浪系数随水深的变化规律是非线性的，造波板前水深由0.6 m逐步增加到0.9 m的过程中，消浪系数先由小变大即由0.43增加至0.73、再由大变小即由0.73降低至0.33，中间的转折点在水深0.7 m。主要原因在于，当水深为0.6 m时，由于水深相对较浅，入射波在防浪林带前约1.0 m位置就发生了较为强烈的破碎，自身的强紊动掺气消耗了大量的波能，剩余波能主要冲击在树干区和约20%的树冠区，因此消浪效果不是十分理想。当水深增加至0.65 m时，入射波在防浪林带前约0.6 m位置发生明显破碎，破碎后的水流冲击了整个树干区及约60%的树冠区，波能在树干区及树冠区明显衰减，消浪效果较好；当水深为0.7 m时，入射波在防浪林带的前部发生破碎，破碎波冲击了整个树干区及树冠区，且基本没有发生淹没，使得防浪林带的消波效果发挥到最大，破碎波的冲击区与树冠层基本重合；当水深大于0.7 m以后，整个防浪林带均处于淹没状态，水深0.75、0.80、0.85和0.90 m的淹没度分别约为10%、40%、65%、75%，消浪系数则分别为0.63、0.53、0.47、0.33，可见随着淹没度的增加消浪系数逐渐降低。

综上所述，水深对消浪效果的影响较大，当水深较浅时，波浪在滩地破碎而产生能量损耗，随后仅以较小的流速及较浅的水深冲击防浪林带，且此时主要是冲击树干区，因此消波效果不佳；随着水深的增加，防浪林的树干区及树冠区与破碎波冲击水流的重合度越来越高，当两者几乎完全重合时，此时的消浪效果最好，当水深继续增大，防浪林带发生一定程度的淹没，此时消浪效果将随淹没度的不断增加而降低。

5 结 语

本文以立面二维自由面紊流模型为工具，建立了基于植物冠层特征的多孔介质模型，精细地模拟了破碎波对植物带的冲击，并与物理模型试验结果进行了对比验证，应用该模型计算分析了植物带宽度、植物密度、滩地水深等因素对消浪效果的影响，具体结论如下：

1)植物区宽度的计算结果显示，防浪林带宽度0.5 m(原体10 m)～1.5 m(原体30 m)区间的消浪系数增长较快，由0.507宽度增加到0.723，防浪林宽度增加1 m(原体20 m)，消浪系数增加了0.216，当防浪林宽度超过1.5 m(原体30 m)后，消浪系数的增幅明显趋缓，每增加1 m(原体20 m)宽防浪林的平均消浪系数仅增大0.029，至防浪林宽度5.0 m(原体100 m)时，消浪系数增大到0.826。

2)植物区种植密度的计算结果显示，当滩地1.5 m(原体30 m)范围内的植物比例(以树冠区计算)由0增长至0.16时，消浪效果呈快速增长趋势，消浪系数由0迅速增长至0.727，从增加的趋势线可以看出，植物比例0～0.08范围内，消浪系数的增长基本处于线性关系，当植物比例大于0.08时，非线性变化较为明显。当植物比例大于0.16时，消浪系数的增幅明显趋缓，植物比例由0.16增加到0.48，增大了2倍，而消浪系数仅增加了15.7%。由此说明防浪林的种植密度存在一个重要拐点，树冠区植物比例大于0.16(相应孔隙率0.84)以后，消浪效果的增长趋缓。

3)滩地水深对消浪效果的影响研究结果表明，水深对消浪效果的影响较大，当水深较浅时，波浪在滩地就发生破碎而自身大量消能，随后仅以较小的流速及较浅的水深冲击防浪林带，且此时主要是冲击树干区，因此消波效果不佳；随着水深的增加，防浪林的树干区及树冠区与破碎波冲击水流的重合度越来越高，当两者几乎完全重合时，此时的消浪效果最好，当水深继续增大，防浪林带发生一定程度的淹没，此时消浪效果将随淹没度的不断增加而降低，直至无限趋近于零。

植物消浪的研究是一个较为复杂的课题，也属于国际上比较前沿的研究领域，数值模拟方法在植物消浪的研究上有重要的作用。植物消浪的模拟精度取决于植物区的概化，而植物区的概化精度则取决于孔隙率的选取是否贴近实际，今后需要更加深入地开展沿海红树林植物特征参数的基础测量工作，包括不同科属、不同树龄的防浪林树干的高度、直径、力学特性，树冠的外形尺寸、体积、孔隙率、枝叶大小、枝叶力学特性，以便支撑物理试验和数模计算。

为使数模研究更贴近实际，在数模建体上，今后应突破将植物区作刚性群杆假设或多孔介质假设取其一的研究方法，应将二者优点结合，即分区建体时在树杆层应用刚性群杆假设的阻力模型、在树冠层应用多孔介质假设的阻力模型，进一步提高数模研究精度。

本文采用的多孔介质模型将植被区考虑为刚性的透孔介质，在用于研究波浪条件、水深条件、滩地条件等对植物消浪的综合影响时具有一定的优势，但是由于无法考虑植物受波浪作用的柔性、晃动等效果，对于植物区内部的消能过程及紊动耗散机理的精细研究上有一定的局限性。

[1] 黄本胜,吉红香.植物护岸对大堤波浪爬高影响试验初探[J].水利技术监督,2005,3:43-46.(HUANG Bensheng,JI Hongxiang.Experimental study on impact of vegetation protection of wave run-up[J].Water Conservancy Supervision,2005,3:43-46.(in Chinese))

[2] 吉红香,黄本胜,邱秀云,等.滩地植物对波浪变形及消浪效果影响试验研究[J].广东水利水电,2008(8):14-18.(JI Hongxiang,HUANG Bensheng,QIU Xiuyun,et al.Experimental study on the wave dissipation effect of the counter-wave plants[J].Guangdong Hydropower,2008(8):14-18.(in Chinese))[3] 白玉川，杨建民，胡嵋，等.植物消浪护岸模型实验研究[J].海洋工程，2005,23(3):65-68.(BAI Yuchuan,YANG Jianmin,HU Mei,et al.Model test of vegetation on the bank to attenuate waves and protect embankments [J].The Ocean Engineering,2005,23(3):65-68.(in Chinese))

[4] KNUTSON P L,R A Brochu,W N Seelig,et al.Wave damping in Spartinaalterniflora marshes[J].Wetlands,1982,2(1):87-104.

[5] MöLLER I T Spencer.Wave dissipation over macro-tidal saltmarshes:Effects of marsh edge typology and vegetation change[J].Journal of Coastal Research,2002(S136):506-521.

[6] MUSLESH F A,CRUISE J F.Functional relationshipsof resistance in wide flood plains with rigid unsubmergedvegetation[J].Journal of Hydraulic Engineering,2006,132(2):163-171.

[7] CHEN H.Numerical study of solitary wave propagating through vegetation[D].National University of Singapore,2010.

[8] 解学超，林鹏智.浅水方程模型模拟刚性非淹没植物阻流特性[J].西南民族大学学报(自然科学版)，2010,5(3)：446-449.(XIE Xuechao,LIN Pengzhi.Numerical simulation of the effects of rigid emergent vegetation on flows using a shallow water equation model [J].Journal of Southwest University for Nationalities(Natural Science Edition),2010,5(3)：446-449.(in Chinese))

[9] LIN Pengzhi,PHILIP L-F Liu.A numerical study of breaking waves in the surf zone[J].J.Fluid Mech.,1998,359:239-264.

[10] RIGHETTI M,ARMANINI A.Flow resistance in openchannel flows with sparsely distributed bushes[J].Journal of Hydrology,2002,269(1-2):55-64.

[11] HARADA K,IMAMURA F.Effects of coastal forest on tsunami hazard mitigation-a preliminary investigation[M].Tsunamis:Case Studies and Recent Developments.2005:279-292.

[12] LIN Pengzhi ,PHILIP L-F Liu.A numerical study of breaking waves in the surf zone[J].J.Fluid Mech.,1998,359:239-264.

Numerical simulation of vegetation-induced wave dissipation in the surf zone

LIU Da1，2,HUANG Bensheng1，2,QIU Jing1，2,TAN Chao1，2

(1.Guangdong Key Laboratory of Hydrodynamic Research,Guangdong Research Institute of Water Resources and Hydropower,Guangzhou 510610,China; 2.State Joint Engineering Laboratory of Estuary Hydraulics,Guangzhou 510610,China)

TV139.2

A

10.16483/j.issn.1005-9865.2016.02.003

1005-9865(2016)02-0016-08

2015-07-11

国家自然科学基金面上资助项目(51279120)；广东水利科技创新重大专题资助项目(2009-29)

刘 达(1981-)，男，博士，高级工程师，E-mail:gdsky_liuda@foxmail.com

黄本胜。E-mail：bensheng@21cn.com