明基床上开孔沉箱稳定性试验研究

董 浩，孙大鹏，吴 浩，冯延奇，行天强，夏志盛

(大连理工大学 海岸和近海工程国家重点试验室，辽宁 大连 116024)

明基床上开孔沉箱稳定性试验研究

董 浩，孙大鹏，吴 浩，冯延奇，行天强，夏志盛

(大连理工大学 海岸和近海工程国家重点试验室，辽宁 大连 116024)

通过水槽内规则波以及不规则波作用下明基床上开孔沉箱的稳定性试验，分析研究了三种基床高度上开孔沉箱的稳定性与相对基床高度、消浪室相对宽度、相对水深、波陡以及开孔率等因素间的相关关系，并利用最小二乘法给出开孔沉箱最小自重与其影响因素间的拟合公式，同时将计算值与试验值进行比较，二者吻合较好，试验结果可供工程设计参考应用。

开孔沉箱；规则波；不规则波；稳定性

Abstract：Through 2-D experiments in the wave-current flume under the condition of regular waves and irregular waves,an experimental investigation has been carried out on the stability of a perforated caisson sitting on the rubble mound foundation.This paper discusses the relationships between three heights of the foundation and main influence factors,such as the relative foundation height,the relative chamber width,the relative depth,the wave steepness,and the porosity of perforated caisson,have been analyzed.A formula is given of the relationship between the minimum weight of perforated caisson and the main influence factors using the least square method(LSM).In addition,comparison of the calculated value with the experimental value shows the consistence of the two values.So the formula can be applied in practical engineering design and application.

Keywords：perforated caisson; irregular waves; regular waves; stability

随着海洋资源的不断开发利用，深海处建造海工建筑物越来越普遍，传统的海工建筑物型式已不能满足实际工程的需要。开孔沉箱作为一种新型的结构型式，越来越受到人们的关注。它具有减少建筑物前波浪反射以及降低工程造价等优点。自20世纪60年代Jarlan[1]提出开孔沉箱防波堤这一新型结构以来，迄今已经进行过许多理论和试验研究。Terrett等[2]以长波理论论证了开孔板的消浪效果并与试验结果相比较；Suh等[3-4]以不同波高和周期的不规则波作为入射波，计算了开孔沉箱的反射率，同时分析了物理模型试验与实际工程相比忽略的一些因素；李玉成等[5]分别研究了规则波和不规则波作用下无顶盖开孔沉箱所受浮托力以及总垂直力之比与消浪室相对宽度、相对水深、开孔率等影响因素的关系并拟合经验公式；2012年张玉彬等[6]进行开孔沉箱后趾总力矩与其影响因素之间的研究，拟合出了明基床上开孔沉箱总垂直力比值与各影响因素之间的经验关系式；2014年夏志胜等[7]分析了开孔沉箱总水平力峰(谷) 值时刻对应的总垂直力与基床相对高度、开孔率、波陡、相对水深、消浪室相对宽度等影响因素之间的关系，并与暗基床的研究成果作了对比讨论。但关于明基床上开孔沉箱稳定性方面的研究成果还鲜有报道，而开展明基床上开孔沉箱稳定性试验研究，涉及工程的结构安全，将对开孔沉箱结构优化设计具有重要的工程应用意义。

1 试验介绍

1.1试验设备及仪器

试验在二维波浪水槽内进行，水槽长56 m、宽0.7 m、最大水深0.7 m，水槽一端安装有液压式造波机，可产生规则波和不规则波，如图1所示。

开孔沉箱试验模型放置在距离造波机35 m位置处，试验基床高度hm分别为0.1、0.15和0.2 m，试验过程中未出现波浪破碎情况；试验水深d保持为0.4 m；开孔率μ为20%和40%；消浪室宽度bc分别为0.15、0.2和0.3 m。试验断面如图1所示，模型如图2所示。

图1 试验模型布置Fig.1 Sketch of experimental model

图3 点压力位置Fig.3 Sketch of distribution of the pressure transducers

在沉箱开孔板迎浪面、背浪面、后实体板和开孔沉箱底板的上面和下面布置多个点压力仪位置如图3所示，图中⊙表示前墙迎浪面和底板测量渗流力点压力布置情况；⨁表示前墙背浪面和底板测量浮托力点压力布置情况。通过采集各个点压力仪的同步时间序列，积分得到结构受到的总水平力和总垂直力。

1.2试验条件

试验条件及波要素如表1所示。

表1 试验条件及无量纲参数范围Tab.1 The condition of experiment and the limits of dimensionless parameters

2 抗滑稳定性试验结果分析

2.1原理

《重力式码头设计与施工规范》[8]中，沿基床底面的抗滑稳定性可按下式计算：

γ0γpP≤(γGVK-γUPU)f

(1)

式中：P为总水平力；PU为总垂直力；VK为沉箱自重；f为摩擦系数，通常取0.6；γ0为结构重要性系数，安全等级二级取1.0；γp为波浪水平力分项系数，取1.2；γG为自重力分项系数，取1.0；γU为波浪垂直力分项系数，取1.2。

由式(1)可得，沉箱结构满足滑移稳定情况下的沉箱自重应满足VK≥(γ0γpP+γUPUf)/(γGf)。

目前计算开孔沉箱满足滑移稳定情况下的沉箱自重，应用规范方法主要是根据《防波堤设计与施工规范》中附录H的有关方法，需要先计算开孔沉箱所受到的最大水平波浪力、最大垂直波浪力以及最大水平波浪力与最大垂直波浪力的相位差，进而通过式(1)计算开孔沉箱满足滑移稳定情况下的沉箱自重，计算流程如图4、图5所示。

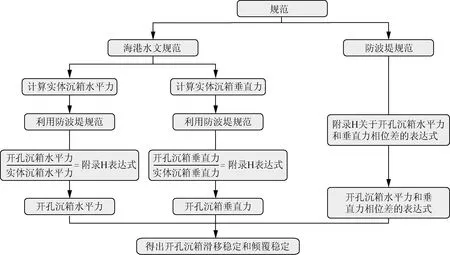
图4 规范方法计算流程Fig.4 Calculation flow chart of the method of the existing standard

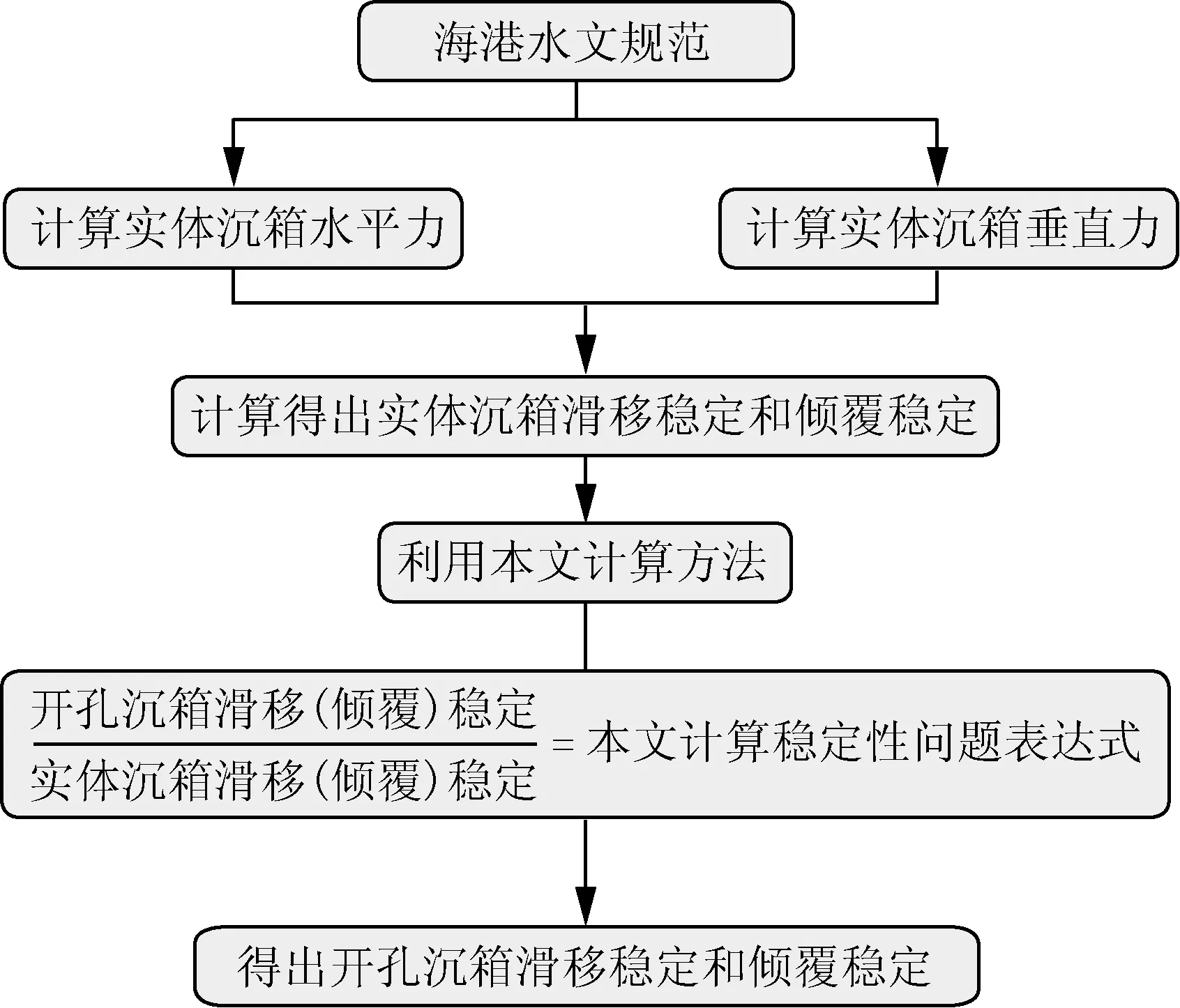
图5 本文方法计算流程Fig.5 Calculation flow chart using the method of paper

由于上述所需计算因素的计算表达式均是通过试验得到的公式，具有一定的误差性。因此，规范计算得出的结果与实际试验测量的结果可能会有一定的误差。

本文采用一种新的计算方式，考虑开孔沉箱稳定性时无需计算开孔沉箱所受到的最大水平波浪力、最大垂直波浪力以及最大水平波浪力与最大垂直波浪力的相位差，而是直接通过于实体沉箱与开孔沉箱的对比得到满足滑移稳定情况下的沉箱自重结果。因此，本文方法相对于规范方法更加便捷。

2.2满足抗滑稳定性条件下，开孔沉箱最小自重的影响因素

用Gmin表示开孔沉箱满足滑移稳定情况下的最小自重、G表示实体沉箱满足滑移稳定情况下的最小自重，以Gmin/G为指标进行分析，由Li等[9]的研究可知，其比值Gmin/G与各因素的关系可由下述表达式表示：

(2)

式中：hm为基床高度，d为试验水深，bc为消浪室宽度，H为试验波高，L为试验波长，μ为开孔率。

本试验通过单因次分析法分析讨论最小自重比Gmin/G与相对基床高度hm/L、相对水深d/L、消浪室相对宽度bc/L、波陡H/L以及开孔率μ等因素的相关关系，并通过最小二乘法拟合得到比值Gmin/G的计算表达式。

2.3规则波作用下的结果分析

规则波作用下，只改变基床高度而保持水深、消浪室宽度、波高、开孔率等因素不变，由图6可见，Gmin/G与hm/L为非线性关系。

图6 只改变相对基床高度得到的Gmin/G与hm/L的关系Fig.6 Relational graph of hm/L versus Gmin/G

规则波作用下，只改变水深而保持基床高度、消浪室宽度、波高、开孔率等因素不变，由图7可见，Gmin/G与d/L为非线性关系。

图7 只改变相对水深得到的Gmin/G与d/L关系Fig.7 Relational graph of d/L versus Gmin/G

规则波作用下，只改变消浪室宽度而保持基床高度、水深、波高、开孔率等因素不变，由图8可见，Gmin/G与bc/L为非线性关系。

图8 只改变相对消浪室宽度得到的Gmin/G与bc/L的关系Fig.8 Relational graph of bc/L versus Gmin/G

规则波作用下，只改变波高度而保持基床高度、水深、消浪室宽度、开孔率等因素不变，由图9可见，Gmin/G与H/L大部分为线性关系。

图9 只改变波陡得到的Gmin/G与H/L的关系Fig.9 Relational graph of H/L versus Gmin/G

由于本次试验中仅有两种开孔率，因此，假设Gmin/G与开孔率μ之间呈线性关系，如图10所示，由图可见，在一定程度上增大开孔率可减小开孔沉箱满足滑移稳定的最小自重。

图10 只改变开孔率得到的Gmin/G与μ的关系Fig.10 Relational graph of μ versus Gmin/G

由以上分析可知Gmin/G与各影响因素的关系，采用最小二乘法拟合Gmin/G与各因素的关系，可得到下述经验关系式：

(3)

上述关系式的相关系数R=0.829 96，为了探讨式(3)的精确性，将式(3)得到的Gmin/G计算值与试验值进行比较，如图11所示，其中实线y=x表示Gmin/G的计算值与试验值相等的直线，由图可见，计算值与试验吻合性较好。

基于海港水文规范关于波浪力的分析计算，可得到不同工况条件下实体沉箱、开孔沉箱满足抗滑稳定最小自重的G值和Gmin值，通过式(3)可得到开孔沉箱Gmin的计算值，进而将规范推荐方法与本文方法计算得出的最小自重进行比较，如图12所示，其中，在进行规范推荐方法计算时，采用《防波堤设计与施工规范》中附录H的有关方法，通过公式附录H的公式计算时，公式中的实体沉箱波浪力采用试验测量值直接代入。由图可见，式(3)给出的开孔沉箱Gmin计算值和规范方法给出的开孔沉箱最小自重计算值与试验值相比，本文方法计算出的结果吻合性更好。

图11 Gmin/G计算值与试验值比较 图12 两种计算方法得到的最小自重比较 Fig.11 Comparison of calculated value with experimental value Fig.12 Comparison of the two methods for calculation

2.4不规则波作用下的结果分析

不规则波作用下，只改变基床高度而保持水深、消浪室宽度、波高、开孔率等因素不变，由图13可见，Gmin/G与hm/L1/3为非线性关系。

图13 只改变相对基床高度得到的Gmin/G与hm/L1/3的关系Fig.13 Relational graph of hm/L1/3 versus Gmin/G

不规则波作用下，只改变水深而保持基床高度、消浪室宽度、波高、开孔率等因素不变，由图14可见，Gmin/G与d/L1/3为非线性关系。

图14 只改变相对水深得到的Gmin/G与d/L1/3的关系Fig.14 Relational graph of d/L1/3 versus Gmin/G

不规则波作用下，只改变消浪室宽度而保持基床高度、水深、波高、开孔率等因素不变，见图15，可见Gmin/G与bc/L1/3为非线性关系。

不规则波作用下，只改变波高度而保持基床高度、水深、消浪室宽度、开孔率等因素不变，见图16，可见Gmin/G与H1/3/L1/3为线性关系。

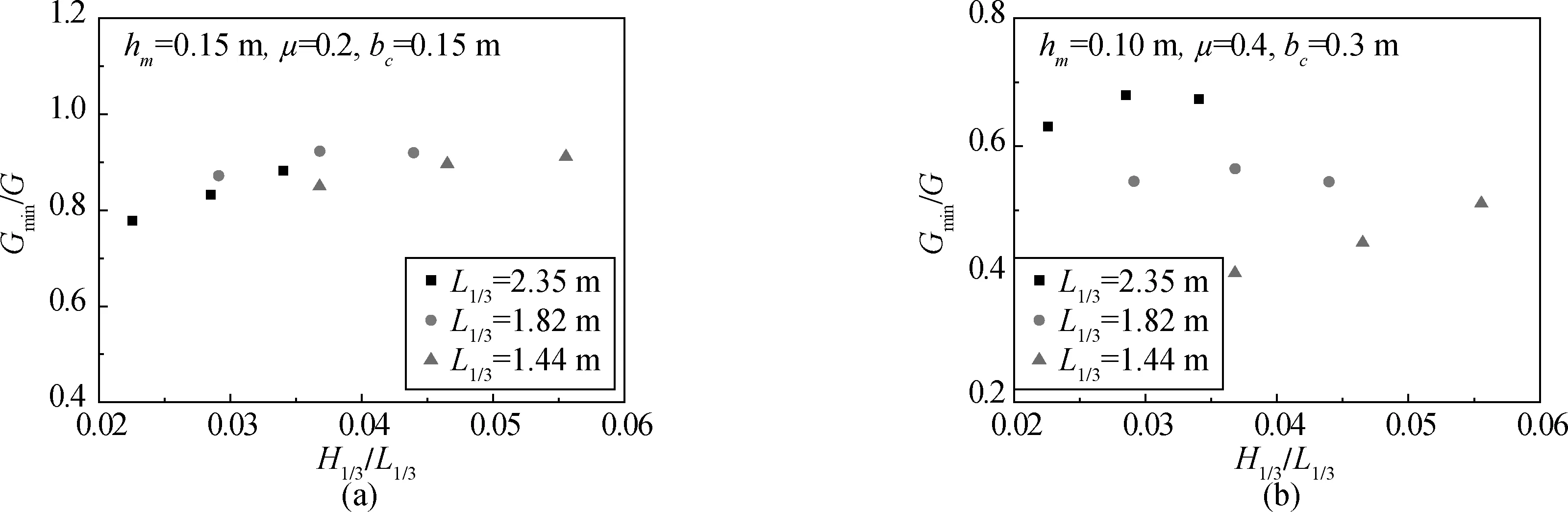
图16 只改变波陡得到的Gmin/G与H1/3/L1/3的关系Fig.16 Relational graph of H1/3/L1/3 versus Gmin/G

由于本次试验中仅有两种开孔率，因此，假设Gmin/G与开孔率μ之间呈线性关系，如图17所示，由图可见，在一定程度上增大开孔率可减小开孔沉箱满足滑移稳定的最小自重。

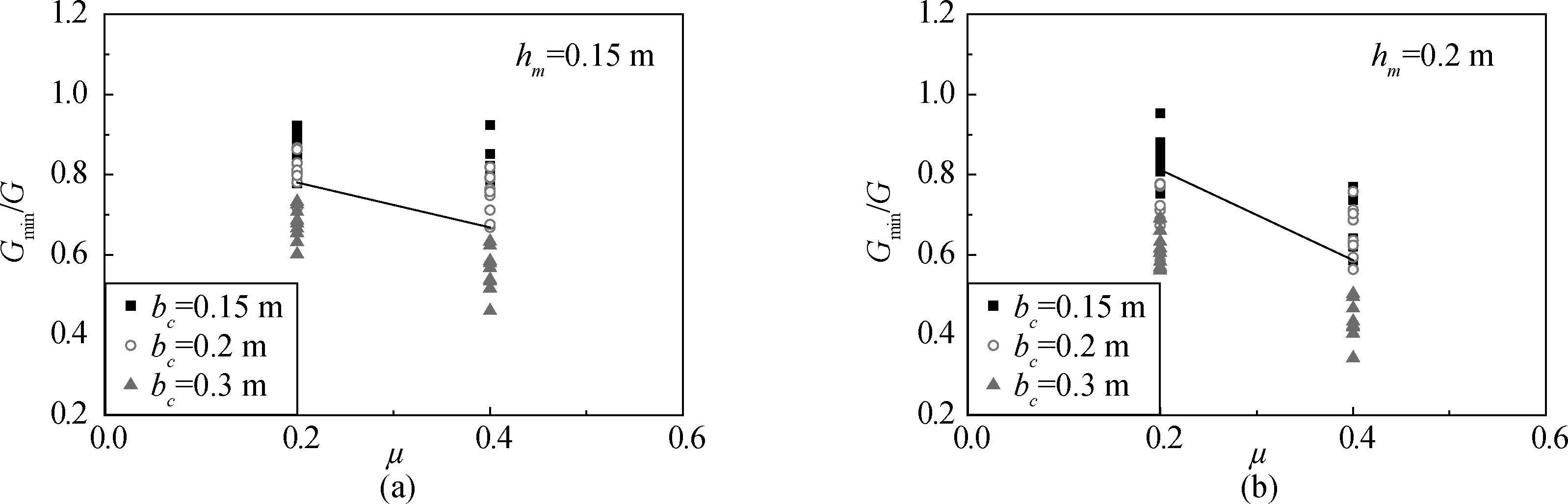
图17 只改变开孔率得到的Gmin/G与μ的关系Fig.17 Relational graph of μ versus Gmin/G

采用最小二乘法拟合Gmin/G与各因素的关系，可得到下述经验关系式：

(4)

上式的相关系数R=0.910 6，为了探讨式(4)的精确性，将式(4)计算得到的Gmin/G值与试验值进行比较，如图18、图19所示，其中实线为y=x，由图可见，计算值与试验值吻合性较好。

采用与计算规则波作用下开孔沉箱满足抗滑稳定性所需最小自重相同的方法，基于海港水文规范关于波浪力的分析计算，可得到不同工况条件下实体沉箱、开孔沉箱满足抗滑稳定最小自重的G值和Gmin值，并通过式(4)可得到开孔沉箱Gmin的计算值，进而将规范推荐方法与本文方法计算得出的最小自重进行比较，如图19所示，由图可见，本文计算方法给出的开孔沉箱Gmin计算值和规范方法给出的开孔沉箱Gmin计算值与试验值相比，本文方法计算出的结果吻合性更好。

2.5小结

1)由上述关于最小自重比Gmin/G与相对基床高度hm/L、相对水深d/L、消浪室相对宽度bc/L、波陡H/L以及开孔率μ等因素的相关关系图可见，最小自重比Gmin/G基本均小于1。因此可知，开孔沉箱对减小沉箱结构满足滑移稳定情况下最小自重具有积极作用。

2)由图12与图19可见，规范计算方法的计算结果离散性较大，主要是由于目前规范进行滑移稳定性分析时，需要先进行开孔沉箱所受最大水平力、最大垂直力以及最大水平力和最大垂直力相位差的计算，而开孔沉箱所受最大水平力与最大垂直力不能直接得出，规范采用南科院试验得出的经验公式进行计算[10]，可能具有一定的误差；因此，在进行稳定性分析时，是在一定的误差基础上进行的，故由规范计算得到的开孔沉箱稳定性分析结果离散性较大。虽然规范方法计算得出的开孔沉箱稳定性分析结果偏于安全，满足工程应用要求，但会造成很大的成本浪费，不符合当前绿色环保的要求，因此有必要进行进一步的研究分析。

3 抗倾稳定性结果分析

3.1研究方法及开孔沉箱重心位置确定

考虑沉箱抗倾稳定性时，应分别考虑波浪力对沉箱前趾以及后趾的力矩，综合比较各种试验工况下波浪力(包括水平力、垂直力)对沉箱前趾和后趾的力矩M前趾、M后趾，如图20所示，可知，开孔沉箱的后趾波浪力矩明显大于前趾波浪力矩。因此，本文考虑后趾的抗倾稳定性。

由于实体沉箱重心位置位于沉箱中部，稳定力臂即重心位置与后趾间的距离y=0.5倍沉箱宽度，因此在确定实体沉箱满足倾覆稳定所需的最小自重时，仅需计算沉箱后趾总力矩与y之比，即为最小自重，但对于开孔沉箱前墙开孔，重心位置未知，故进行最小自重计算时，需先确定重心位置，进而确定稳定力臂y值。

按照《重力式码头设计与施工规范》[6]，对于沉箱细部尺寸：外壁厚≮0.25 m，一般可取0.3、0.35及0.4 m；底板厚度一般比壁厚大0.05～0.1 m；隔墙厚度≮0.2 m；加强角宽度0.15～0.2 m。本文取如下三种情况进行计算分析：1)壁厚0.3 m、底板厚度0.45 m、隔墙厚度0.2 m，加强角0.2 m；2)壁厚0.35 m、底板厚度0.45 m、隔墙厚度0.2 m，加强角0.2 m以及3)壁厚0.4 m、底板厚度0.5 m、隔墙厚度0.2 m，加强角0.2 m。沉箱结构形式如图21所示。

图20 波浪力对开孔沉箱前趾、后趾力矩的比较Fig.20 Comparison of torque of fore-toe with torque of hind-toe on perforated caisson

图21 沉箱结构断面(单位：cm)Fig.21 Profile of caisson structure(unit: cm)

若用y表示沉箱自重对后趾的稳定力臂，则第一种情况下，实体沉箱稳定力臂y=4.5 m，20%开孔率的开孔沉箱稳定力臂y=4.38 m，40%开孔率的开孔沉箱稳定力臂y=4.25 m；第二种情况下，实体沉箱稳定力臂y=4.5 m，20%开孔率的开孔沉箱稳定力臂y=4.37 m，40%开孔率的开孔沉箱稳定力臂y=4.23 m；第三种情况下，实体沉箱稳定力臂y=4.5 m，20%开孔率的开孔沉箱稳定力臂y=4.36 m，40%开孔率的开孔沉箱稳定力臂y=4.22 m。综上，第三种情况下开孔沉箱稳定力臂y最小，应视为最不利情况。故本文以第三种情况下的沉箱结构进行倾覆稳定计算分析。

3.2开孔沉箱稳定性结果分析

由前节对开孔沉箱稳定力臂y的分析，开孔沉箱满足滑移稳定情况的最小自重对后趾的稳定总力矩为M1=y*Gmin。比较M1与开孔沉箱后趾所受波浪力的总力矩M后趾，如图22所示。M1大于M后趾，可知开孔沉箱满足滑移稳定所需最小自重大于满足倾覆稳定所需最小自重，即综合考虑沉箱的抗滑和抗倾稳定性，以满足滑移稳定情况的最小自重为控制自重。

图22 满足滑移稳定的稳定力矩M1与波浪力总力矩M后趾的对比Fig.22 Comparison of torque of wave with steady torque meeting the requirements of anti-sliding

4 结 语

本次试验采用三种基床高度，分析探讨了消浪室相对宽度、相对水深、相对波高、相对基床高度以及开孔率对开孔沉箱稳定性的影响规律，结论如下：

1) 通过滑移稳定与倾覆稳定的分析、比较，在开孔沉箱结构设计时，以满足滑移稳定情况的最小自重为控制自重。

2) 给出了满足开孔沉箱稳定性所需最小自重与相对消浪室宽度、相对水深、相对波高、相对基床高度以及开孔率的关系式。

3) 通过对本文开孔沉箱最小自重Gmin计算值、规范方法计算值与试验值的比较，可知，本文计算方法得到的Gmin计算值与试验值吻合更好，建议工程设计参考应用。

本文采用的计算方法，不需计算开孔沉箱所受的水平力与垂直力，而是直接通过开孔沉箱稳定性与实体沉箱稳定性的试验公式，直接得出开孔沉箱稳定性分析结果，计算结果简单，离散性较小，且满足工程应用要求，因此具有一定的参考价值。

[1] JARLAN G E.A perforated vertical wall breakwater[J].The Dock and Harbour Authority,1961,41(486)：394-398.

[2] TERRETT F L,OSORIO J,LEAN G H.Model studies of a perforated breakwater[C]// ASCE.1968.

[3] SUH K D,CHOI J C,KIM B H,et al.Reflection of irregular waves from perforated-wall caisson breakwaters[J].Coastal Engineering,2001,44(2)：141-151.

[4] SUH K,PARK J K,PARK W S.Wave reflection from partially perforated-wall caisson breakwater[J].Ocean Engineering,2006,33(2)：264-280.

[5] 李玉成,姜俊杰,孙大鹏,等.规则波作用下无顶盖开孔沉箱所受垂直力的实验研究[J].中国海洋平台，2004,19(2)：14-21.(LI Yucheng,JIAN Junjie,SUN Dapeng,et al.Experimental study of vertical forces acting on perforated caisson under irregular waves[J].China Offshore Platform，2004,19(2)：14-21.(in Chinese))

[6] 张玉彬,孙大鹏,夏志盛.明基床上开孔沉箱总力矩试验研究[J].海洋工程，2012,30(3)：51-58.(ZHANG Yubin,SUN Dapeng,XIA Zhisheng.Experimental study of the total moments acting on perforated caisson on rubble mound foundation[J].The Ocean Engineering,2012,30(3)：51-58.(in Chinese))

[7] 夏志盛,孙大鹏,张玉彬,等.不规则波作用下明基床上开孔沉箱垂直力分析[J].海洋工程，2014,32(5)：15-24.(XIA Zhisheng,SUN Dapeng,ZHANG Yubin,et al.Analysis on total vertical forces of perforated caisson mounted on rubble mound foundation under irregular waves[J].The Ocean Engineering,2014,32(5)：15-24.(in Chinese))

[8] JTS 167-2-2009.重力式码头设计与施工规范[S].中华人民共和国交通部，2009.(JTS 167-2-2009.Code for design and construction of gravity wharf[S].2009.(in Chinese))

[9] LI Y C.Wave action on maritime structures[M].Dalian：the Press of Dalian University of Technology,1989.

[10] 防波堤设计与施工规范[S].中华人民共和国交通部，2011.

Experimental study of stability of perforated caisson with rubble foundation

DONG Hao，SUN Dapeng，WU Hao，FENG Yanqi，XING Tianqiang，XIA Zhisheng

(State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116024，China)

TV139.2

A

10.16483/j.issn.1005-9865.2016.05.004

1005-9865(2016)05-0030-10

2016-01-04

国家自然科学基金资助项目(51279027；51221961)

董浩(1990-)，男，天津人，硕士研究生，主要从事海岸和近海工程研究。E-mail：lanmangyi@mail.dlut.edu.cn