半潜平台锚泊辅助动力定位时域模拟研究
贺华成,王 磊,金 鑫,徐胜文
(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.高新船舶和深海开发协同创新中心,上海 200240)
半潜平台锚泊辅助动力定位时域模拟研究
贺华成1,2,王 磊1,2,金 鑫1,2,徐胜文1,2
(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.高新船舶和深海开发协同创新中心,上海 200240)
随着海洋油气资源开发逐渐走向深海,浮式结构物的定位能力越来越受到人们的重视。锚的泊辅助动力定位系统是将锚泊定位和动力定位相结合的一种新型海上定位系统。它具有安全性高、定位能力强、消耗功率小的特点。本文以某深水半潜式钻井平台为例,通过建立锚泊辅助动力定位时域模拟程序,分析平台在工作海况下的定位精度和功率消耗,并与相应海况下的动力定位进行比较。分析结果表明,该时域模拟程序能较为准确的地反映实际平台的定位情况。与动力定位相比,锚泊辅助动力定位能够取得更好的定位精度和较小的功率消耗,是更理想的定位方式。
锚泊辅助动力定位;定位精度;功率消耗
Abstract:The higher demand of oil and gas has led to their exploitation and exploration in harsher and deeper waters.The capability to keep position with high accuracy of floating structures has been more and more concerned.Mooring assisted dynamic positioning system is a new positioning system combining mooring system with dynamic positioning system.It has the advantages of high safety,high positioning accuracy and low power consumption.With a certain deep water semi-submersible drilling platform as an example,this paper is dedicated to analyzing the positioning accuracy and power consumption by establishing a time-domain simulation program of positioning mooring system.Comparisons are made between dynamic positioning system and positioning mooring system.The comparisons show that the time-domain simulation can accurately reflect the practical positioning conditions of the platform.Compared with dynamic positioning,positioning mooring is a reasonable positioning method with better positioning accuracy and less power consumption.
Keywords:positioning mooring system; positioning accuracy; power consumption
随着世界石油需求的激增,海洋工程迫切需要向深水领域发展。对于海洋浮式钻井系统来说,经常需要定位于某一精度范围内进行钻井、铺管、输油等各种作业,定位系统是保证其海上正常生产作业的重要设备[1]。浮式结构物传统的定位方式有锚泊定位和动力定位。对于深水作业,锚泊系统的抓地力减小,锚链长度和重量急剧增加,造价提高的同时,定位效果却并不理想。动力定位系统不仅能在深水中实现精确定位,且成本不随水深的增加而增加,但该系统功率较大,需要消耗较多的能源[2]。
锚泊辅助动力定位系统是锚泊定位和动力定位相结合的一种新型海上定位系统。它既能满足平台在较恶劣海况下的定位能力需求,防止锚泊系统的断裂失效,又能降低动力定位时的燃油消耗,在深水作业中非常实用[3,4]。自20世纪80年代以来,锚泊辅助动力定位在商业上得到广泛应用,且在海洋石油开采工程的固定式平台中显示出不同寻常的经济效益[5]。但关于锚泊辅助动力定位系统的研究都是基于20世纪70年代以来的经验[6],国际上只有少数海洋工程研究机构开展了锚泊辅助动力定位的理论研究,并进行了相关的模型试验。
Strand[7]首次在动力定位系统的设计中考虑锚泊系统的回复力,建立了锚泊辅助动力定位系统的数学模型。Aamo[5]提出了一种张力反馈系统,通过实时测量系泊缆上的应力,将其作为反馈信号进入动力定位控制器,从而缓解锚链的负载,降低锚泊系统失效的概率。Berntsen[8]则将锚链线上的张力直接作为动力定位控制器的一部分,在设计阶段就考虑锚泊系统的失效,进一步提高了系统的安全性。孙攀[9]针对一艘半潜式钻井平台,对比分析了其在动力定位和锚泊辅助动力定位下的定位精度和功率消耗,验证了锚泊辅助动力定位系统的优越性。
本文以一艘深水半潜式钻井平台为例,通过建立锚泊辅助动力定位时域模拟程序,分析其在给定工作海况下的定位精度和功率消耗,为以后工程实际应用提供重要的理论依据。
1 动力定位系统的数学模型
1.1坐标系定义
在动力定位系统中,通常采用如图1所示的三组坐标系表示。

图1 坐标系的定义Fig.1 Definition of coordinate frames
1)大地坐标系(XEYEZE-frame)
该坐标系用于测量船舶相对于定义原点的位置和艏向角,每个位置参考系统(例如全球定位系统(GPS)、水声参考系统等)的局部坐标系都是通过一个共同的地球固定坐标系平移得到的。
2)动坐标系(XYZ-frame)
该坐标系固定于船上并且随船一起运动,坐标原点通常选取在船舶的重心位置。船舶的运动和受力在动坐标系中表达。
3)参考平行坐标系(XRYRZR-frame)
该坐标系也可称为水动力坐标系,通常是沿着船舶航行轨迹进行平面运动,不随船舶摇荡。在动力定位系统中,该坐标系固定于定位的目标点,XR轴正向即为动力定位的目标艏向角。
大地坐标系中船舶的位置和欧拉角(η∈6)与动坐标系中船舶的速度(ν∈6)可以通过转换矩阵J(η)∈6×6求得,其关系式为[10]:
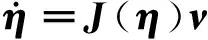
(1)
如果只考虑水平面内的三自由度运动,则速度关系式可简化为:

(2)

(3)
1.2非线性低频运动
在动力定位系统的研究中,通常将船舶的运动分为非线性的低频运动,和线性的波频运动[11]。动力定位主要考虑船舶的低频运动模型,其运动方程可以表示为:
(4)
式中:M∈6×6为船舶质量矩阵,包括附加质量;CRB(ν)∈6×6和CA(ν)∈6×6分别为船舶刚体和附加质量的科氏力和向心力作用矩阵;D(νr)∈6为船舶受到的阻尼力,是关于船舶与流的相对速度νr∈6的函数;G(η)∈6为广义回复力,由浮力和重力产生;τenv∈6为风力和二阶波浪力,流力已包含在相对速度νr中;τmoor∈6为锚泊系统的回复力,后文会详细介绍;τc∈6为动力定位系统的控制向量,包括推进系统产生的推力和力矩。
1.3线性波频运动
线性波频运动方程可以表示为:

(5)

(6)
式中:ηRw∈6为参考平行坐标系中的波频运动向量,ηw∈6为大地坐标系中的波频运动向量,6为一阶波浪激励力,它受波浪频率和船舶与波浪间的夹角的影响,M(w)∈6×6为系统的惯性矩阵,包括船舶刚体的质量和附加质量,DP(w)∈6×6为波浪辐射阻尼矩阵,G∈6×6为线性回复力矩阵,是由重力和浮力引起,只影响船舶的垂荡、横摇和纵摇。对于系泊船舶,可以认为锚泊系统对于波频运动没有影响[12]。
1.4波浪载荷
在平台的低频运动模型中,风力和流力采用定常力,由模型试验测得,唯一随时间变化的是二阶波浪力。二阶波浪力包括平均漂移力、低频(差频)力和高频(和频)力三个部分,其大小与入射波的平方成正比。假定入射的不规则波用谐波的叠加来表示,则二阶波浪力(忽略高频部分)可以通过二次传递函数(QTF)来表示[13]:
(7)
式中:ωi是波浪频率,ζi是波幅,εi是随机相位角。二次传递函数Pij和Qij的计算非常耗时,一般通过商业软件来计算,本文的QTF由频域计算软件HydroStar计算得到。
1.5锚泊系统模型
锚泊系统由一组通过转塔连接或者直接连接到船舶上的锚链线组成。在锚泊辅助动力定位系统的设计中,通常将锚泊系统的影响在船舶低频运动模型中进行考虑。水平分布的锚泊模型可以用以下公式表示:
τmoor=-J-1(η2)gmo(η)-dmo(νr)
(8)
式中:dmo为由于锚泊系统存在而产生的附加阻尼力向量,gmo∈3大地坐标系下的回复力向量:
(9)
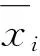
(10)
水平回复力Hi也可以通过每根锚链线的静态特性(力/位移的关系)来表达:
(11)
即水平回复力Hi可以直接表示为导缆孔与抛锚点之间水平距离hi的函数,fHi(hi)可以通过对锚链线进行静态分析得到。由于在锚泊辅助动力定位系统中,锚泊系统仅起辅助作用,因此采用锚泊系统的准静态模型对锚泊辅助动力定位进行时域模拟,分析其定位能力是合理的。在本文中,锚泊系统在水平面内的静态刚度由商业软件OrcaFlex计算得到。
1.6控制系统与推力分配
时域模拟程序的控制系统模型采用经典的PID控制。在水平方向上三个自由度的PID控制方法如下式所示:
(12)
PID控制中的三个系数比弹簧-阻尼模型具有明显的物理意义。实际上,采用PID控制策略的动力定位系统即为海洋结构物在水平面内提供了回复刚度和一部分运动阻尼。积分系数用于消除稳态误差,通常情况下取为零。
推力分配策略将控制系统输出的推力分配到各个推进器上,通过求解如下最优化问题的最小值的解来获得推力分配的结果[14]:
(13)
式中:Ti是第i个推力器的推力,n是推力器的数目,C是权重系数,αi是推力器的方向,xi和yi是推力器相对于船舶重心的位置。可以通过设置禁止角即对αi的取值范围加以限制来减小推力器之间的水动力干扰。一旦求得各个推力器的推力,对应的功率可以通过下式计算:
(14)
式中:D为螺旋桨直径,KT为推力系数,KQ为转矩系数,KT、KQ可根据轴向进速在螺旋桨敞水性能曲线上查取。
2 数值模拟实例
2.1半潜平台参数
研究对象为装备有锚泊辅助动力定位系统的深水半潜平台,平台工作水深为1 500 m。平台的主要组成部件包括:下浮体2个、柱形横撑杆2个、立柱4根、主甲板、箱型甲板、居住舱楼、井架台、井架、起重机、直升机平台等。平台主要参数见表1。

表1 半潜平台主要参数Tab.1 Main parameters of the platform
动力定位系统中推力器采用8个全回转推进器并配备导管,推进器参数见表2。推力器布置为“内八”形式,T1~T8代表1号到8号推力器。1、4、5、8号推力器到横纵中心线距离分别为15.70 m 和35.50 m,2、3、6、7号推力器到横纵中心线距离分别为47.02 m和24.58 m,如图2所示。这种布置的优势在于拉大了推力器之间的距离,能够有效降低桨-桨干扰。

表2 推力器参数Tab.2 Parameters of thrusters
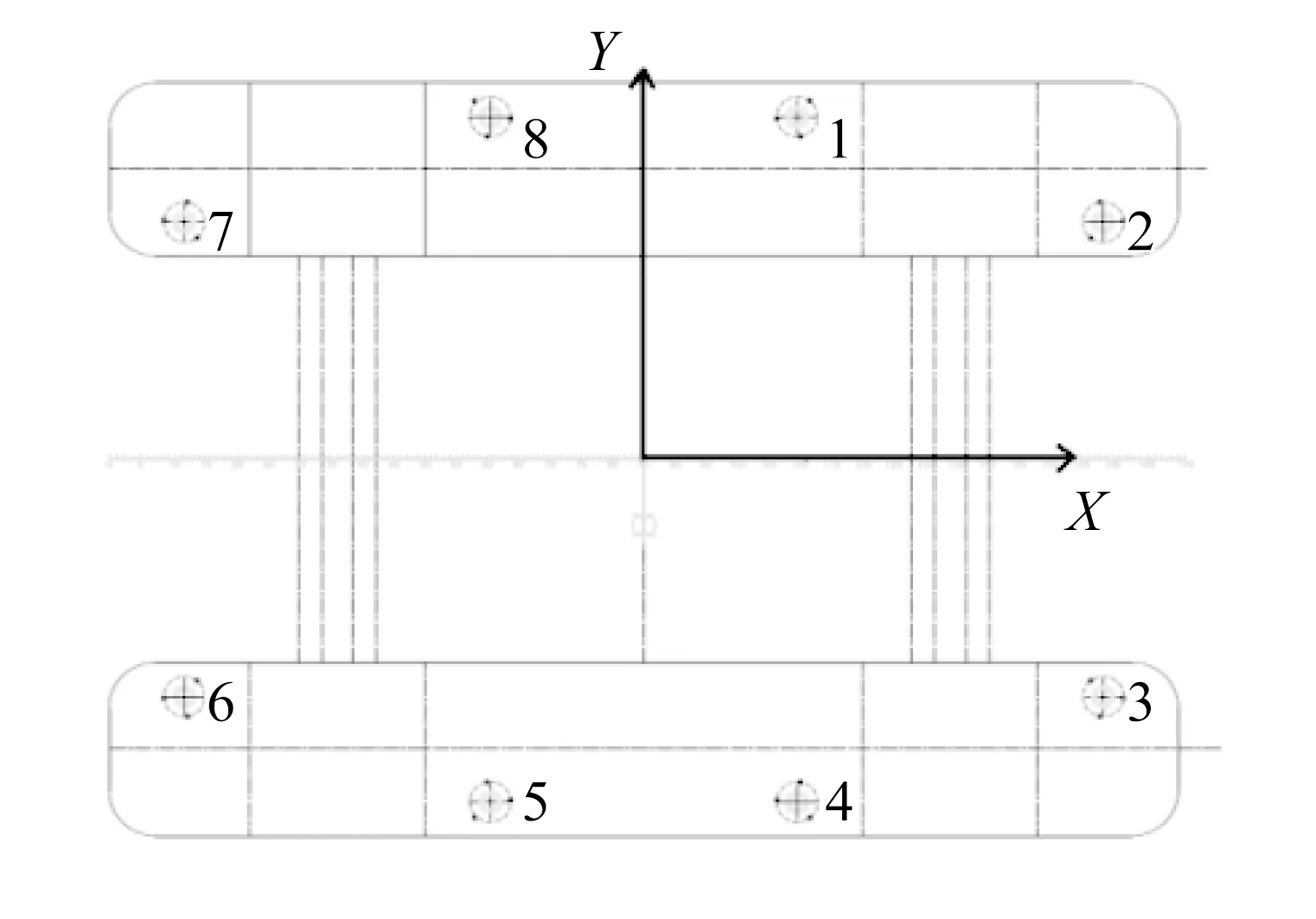
图2 推力器布置示意Fig.2 Layout of the thrusters

图3 锚泊系统布置示意Fig.3 Layout of the mooring system
2.2锚泊系统
锚泊系统由4组、每组2根共8根相同的组合系泊链组成。从海底到海面各部分材料的长度分别为:底部锚链长度1 850 m,中部尼龙绳(Polyester)长度2 650 m,顶部锚链长度150 m,布置形式如图3所示。由OrcaFlex软件计算得到的锚泊系统的水平刚度曲线如图4所示。

图4 锚泊系统的水平刚度Fig.4 Static stiffness of the mooring system in X(Y) direction and around Z axis
2.3海洋环境载荷
由于风、浪、流同向作用时为最恶劣的环境条件,故取风、浪、流同向联合作用作为计算的环境条件,其具体参数如表3所示。
3 时域模拟和分析
通过自主编写的锚泊辅助动力定位时域模拟程序,对半潜平台在180°,90°和135°环境载荷下的锚泊辅助动力定位(PM)分别进行时域模拟,并与相应工况下的动力定位(DP)进行比较,结果分析如表4所示。
由于在180°环境力的作用下,Y方向上的位移和艏摇都是小值,不具有比较意义,因此表4中仅列出了平台在X方向上的偏移和功率统计。由表4可知,无论是锚泊辅助动力定位还是动力定位,平台在180°环境载荷的作用下均能保持良好的平均位置,X方向上的平均偏移分别为-0.131 2 和-0.137 8 m。然而,平台在平均位置附近的往复运动非常剧烈,标准差较大,其偏移的最大距离分别为-20.467 8 和-23.981 5 m。图5为平台在X方向上偏移的时历曲线,从图中可以清楚地看到,定位情况并不稳定。

表3 环境条件Tab.3 Environmental condition

表4 180°时域模拟结果Tab.4 Simulation results in 180°direction

图5 180°偏移Fig.5 Offset in 180° direction

图6 180°方向上的二阶波浪力Fig.6 Second-order wave loads in 180° direction
产生这种剧烈往复运动的原因主要有二个方面。首先,平台的形状导致了其在180°方向上对水流阻力较小,进而在纵荡方向上的附加质量也较小,即平台更容易在环境载荷的作用下产生大范围运动。另外,180°方向上的环境载荷变化较为剧烈,由于计算中风速和流速都为定常值,二阶波浪力是唯一随时间变化的外载荷。180°方向上的二阶波浪力如图6所示。
由上图可知,二阶波浪力与平台的偏移有着直接的关系。在1 500 s左右时,二阶波浪力出现峰值,同时平台在X方向上的偏移也出现峰值。当环境力剧烈变化时,平台的定位情况也就很难稳定。如果在动力定位系统中采用环境力前馈控制策略,则能有效地改善这种由环境力剧烈变化引起的大范围往复运动。
就定位精度而言,二种定位方式的差别不大,总体上,锚泊辅助动力定位要稍好于动力定位。但大范围的往复运动会对系统的功率消耗产生显著的影响。由表4可知,两种定位方式的平均总功率分别为7 123和8 742 kW。与动力定位相比,锚泊辅助动力定位下推进器的功率消耗有了显著的改善,平均值减小了18.5%。这是因为在平台大范围的往复运动中,锚泊系统提供了大量的回复力,从而减轻了动力定位系统推进器的负载,大大降低了系统的功率消耗。

表5 90°时域模拟结果Tab.5 Simulation results in 90° direction

图7 90°偏移Fig.7 Offset in 90°direction
表5所示为平台在90°环境载荷作用下的时域模拟结果,与180°类似,表中仅列出了平台在Y方向上的偏移和功率统计。由表5可知,在90°环境载荷的作用下,平台不仅能保持良好的平均位置,而且在平均位置附近的往复运动也较小,最大偏移分别为-6.324 1和-7.300 4 m,定位十分精确。一方面这是因为平台在横荡方向上的附加质量较大,不易受到环境力的扰动;另一方面则是因为90°方向上的二阶波浪力变化较为缓和,峰值较小,无法引起平台的大范围偏移。平台在Y方向上偏移的时历曲线如图7所示。
从功率消耗上看,两种定位方式的平均总功率非常接近,分别为8 948和9 207 kW,动力定位的功率消耗稍大。这是因为平台的定位精度很高,在平衡点附近的往复运动较小,锚泊系统只提供了很小的回复力,不能显著地降低系统的功率消耗,主要的定位工作仍由动力定位系统的推进器来完成。

表6 135°时域模拟结果Tab.6 Simulation results in 135° direction

就定位精度而言,锚泊辅助动力定位要明显优于动力定位。平台在锚泊辅助动力定位下,平均偏移半径1.968 7 m,仅为动力定位的35.98%,最大偏移半径9.920 5 m,也仅为动力定位的42.94%;而且艏摇角的标准差远小于动力定位,即锚泊辅助动力定位对于艏向的控制更加稳定,这一点时历曲线可以清楚的看到。同时,锚泊辅助动力定位下,平台的功率消耗相比动力定位也有了很大的改善,其平均功率9 817kW,较动力定位减少了13.65%。

图8 135°偏移半径Fig.8 Offset radius in 135° direction
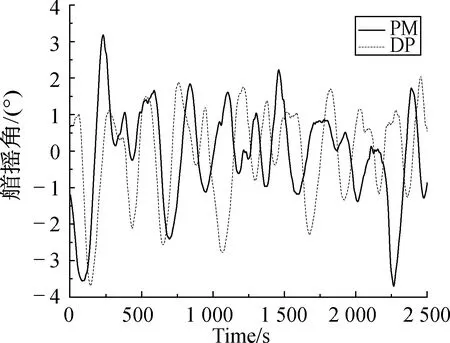
图9 135°艏摇Fig.9 Yaw in 135° direction
4 结 语
以某深水半潜式钻井平台为例,通过建立锚泊辅助动力定位时域模拟程序,分析平台在工作海况下的定位精度和功率消耗,并与相应海况下的动力定位进行比较。
由分析结果可知,该时域模拟程序能较为准确地反映实际平台的定位情况。当外界环境力剧烈变化时,平台将产生大范围的往复运动,与动力定位相比,锚泊辅助动力定位不仅能实现更高精度的定位,而且能大大降低推进器的功率消耗,降低动力定位系统的燃油消耗。然而,锚泊系统的安装布置与拆卸所花费的时间长,平台工作地点变动的成本相对较高。而且,当水深增加时,布置锚泊系统的成本亦随之大幅增加。因此,在作业地点相对固定,工作水深在合理范围内时,锚泊辅助动力定位是一种更为理想的定位方式。
[1] 金秋,张国忠.世界海洋油气开发现状及前景展望[J].国际石油经济,2005.(JIN Qiu,ZHANG Guozhong.Present situation and prospect of world marine oil and gas development[J].International Petroleum Economics,2005.(in Chinese))
[2] 赵志高,杨建民,王磊,等.动力定位系统发展状况及研究方法[J].海洋工程,2002,20(1):91-97.(ZHAO Zhigao,YANG Jianmin,WANG Lei,et al.The development and research method of dynamic positioning system [J].The Ocean Engineering,2002,20(1):91-97.(in Chinese))
[3] 孙攀.深海半潜式钻井平台锚泊辅助动力定位系统研究[D].上海交通大学,2011.(SUN Pan.Research on position mooring system of a deep water semi-submersible drilling platform[D].Shanghai Jiao Tong University,2011.(in Chinese))
[4] WICHERS J,Van DIJK R.Benefits of using assisted DP for deepwater mooring systems[C]//Offshore Technology Conference.1999.
[5] AAMO O M,FOSSEN T I.Controlling line tension in thruster assisted mooring systems[C]// Proceedings of IEEE International Conference on Control Applications.1999,2:1 104-1 109.
[6] SøRENSEN A J,SAGATUN S I,FOSSEN T I.Design of a dynamic positioning system using model-based control[J].Control Engineering Practice,1996,4(3):359-368.
[7] STRAND J P,SøRENSEN A J,FOSSEN T I.Modelling and control of thruster assisted position mooring systems for ships [J].Modeling Identification and Control,1998,19(2): 61-76.
[8] BERNTSEN P I B,AAMO O M,LEIRA B J.Ensuring mooring line integrity by dynamic positioning:Controller design and experimental tests[J].Automatica,2009,45(5):1 285-1 290.
[9] 孙攀,王磊,王亮.深水半潜平台锚泊辅助动力定位系统功率消耗研究[J].海洋工程,2010,28(3):24-30.(SUN Pan,WANG Lei,WANG Liang.Research on power consumption of position mooring system for a deep sea semi-submersible platform[J].The Ocean Engineering,2010,28(3):24-30.(in Chinese))
[10] WOOLSEY C A.Review of marine control systems:Guidance,navigation,and control of ships,rigs and underwater vehicles[J].Journal of Guidance,Control,and Dynamics,2005,28(3): 574-575.
[11] FOSSEN T I.Handbook of marine craft hydrodynamics and motion control[M].John Wiley & Sons,2011.
[12] Triantafyllou M S.Cable mechanics for moored floating systems[J].Floating Structure,1994.
[13] Faltinsen O M.Sea loads on ships and offshore structures [M].New York,Cambridge University Press,1990,10(1).
Research on time-domain simulations of mooring-assisted dynamic positioning system for a semi-submersible platform
HE Huacheng1,2,WANG Lei1,2,JIN Xin1,2,XU Shengwen1,2
(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China; 2.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China)
P751
A
10.16483/j.issn.1005-9865.2016.05.014
2015-09-22
国家自然基金资助项目(51179103);中国国家重点基础研究发展计划资助项目(2013CB036103)
贺华成(1991-),男,湖北洪湖人,硕士研究生,主要研究方向为船舶动力定位。E-mail:hhc_sjtu@163.com
王磊。E-mail:wanglei@sjtu.edu.cn

