应用两次展开法求解系泊柱体慢漂运动方程

金瑞佳，滕 斌，吕 林

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

应用两次展开法求解系泊柱体慢漂运动方程

金瑞佳，滕 斌，吕 林

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

在深海中系泊的海洋平台，如Spar平台，水下部分为带有系泊的圆柱结构，其水平方向运动响应往往具有较低的自振频率，容易在低频波浪力(源于非线性的差频效应)作用下发生共振响应，使结构发生大幅水平慢漂。当浮体的瞬时位置大幅偏离初始位置时，基于初始平衡位置的摄动展开法会存在较大误差。针对这一问题，采用两次展开方法，对大幅慢漂运动开展时域模拟研究。对双色波作用下自由漂浮圆柱的大幅运动响应问题进行数值分析，并与采用基于初始平衡位置的摄动展开法的计算结果进行了对比。结果表明，采用新的两次展开法可以计算出波浪遭遇频率的变化和波浪漂移阻尼，而这无法从基于初始平衡位置的常规摄动展开法中得到，体现了两次展开法在分析大幅慢漂问题上的优势。

两次展开；二阶时域方法；小波变换；大幅慢漂；波浪漂移阻尼

Abstract：Large drift phenomenon of Spar platform is often observed in deep sea,whose natural frequency in horizontal direction is very low because the difference frequency of the nonlinear wave is close to the natural frequency of the structure.There is a large error if the perturbation expansion based on the initial equilibrium location is adopted when the floater is far away from the initial equilibrium position.For this reason,a twice-expansion time domain method is employed in this paper to study the problem.Using this method,the motion response of a free cylinder is evaluated,and the results are compared with those by perturbation expansion method based on initial equilibrium location.The comparisons show that the twice-expansion method demonstrates the performance on calculating the change of encountering frequency between waves and structures as well as the wave drift damping,while the original method does not.This shows the advantages of the twice-expansion method in solving the large drift problem.

Keywords：twice expansion; second-order time domain method; wavelet transform; large drift motion; wave drift damping

深海中的大型海洋平台，如Spar平台，通过锚泊系统定位于海中，水下部分为圆柱结构。Spar平台系统在水平运动方向通常具有很低的固有频率，特别容易在非线性波浪差频的作用下发生大幅度的水平往复慢漂运动。当平台发生大幅慢漂现象时，若将参考系设置在结构物上，则可以简化为水流与结构物的相对运动问题。关于这类问题，Nossen等人[1]在频域内计算了三维固定在波流环境中受到的一阶波浪力，而没有涉及运动物体的求解计算。Kinoshita和Bao[2,3]通过理论推导获得了单个圆柱和一列圆柱在波浪和水流中的波浪力和波浪漂移阻尼，但理论推导具有一定的局限性，不能计算任意形状的物体。Kim[4]和Liu[5]随后在时域内求解了波流与结构物的耦合作用产生的一阶运动响应，但未计算高阶次的问题。上述学者研究的都是水流流速不变情况下的波浪与结构物耦合问题，而对于浮体结构物的大幅慢漂问题，漂移速度一直在变化，因此相当于变速水流与波浪中结构物的相对运动问题，至今相关研究较少。

同时，针对海洋平台系泊系统以及波浪的非线性，大量学者开展了相关的研究工作。Sarkar和Eatock Taylor[6,7]提出了对波陡和系泊缆索非线性的双参数展开方法，并采用半解析的方法计算了有限水深中带有系泊缆索的截断圆柱问题。Ormberg和Larsen[8]、Kim[9,10]、Garrett[11]计算了船体与系泊缆索的耦合作用，这些工作主要关注了系泊缆索的计算方法，而水动力荷载部分则采用比较简单的线性模型。Low[12-14]同样认为，深水结构物和浮体的耦合作用中存在大量的非线性影响，并提出一种时域和频域混合的方法，求解结构物的运动响应和系泊系统的张力。Kim等人[15]采用基于频域摄动展开的Cummins方法计算了波浪荷载下漂浮结构物的水动力荷载。Yang等人[16,17]采用时域的摄动展开法计算水动力荷载。上述的摄动展开均是直接基于初始平衡位置进行，没有考虑结构物发生大幅慢漂现象对分析结果的影响。

深海结构物的大幅度慢漂运动，其幅度甚至会大于波长尺度。在此种情况下，若仍采用基于初始平衡位置的摄动展开法，无法准确满足摄动展开的小振幅假设，计算会存在较大误差，而且也无法考虑由于物体运动导致波浪力相位的变化和入射波浪与结构物遭遇频率的变化。此外，基于初始平衡位置的摄动展开法无法计算结构物发生大幅慢漂运动时产生的波浪漂移阻尼，这部分阻尼会影响结构物的自振频率和运动响应幅值。基于上述原因，本文采用了一种在时域内求解波浪与结构物相互作用的两次展开的方法。其中，结构物的运动被分解为两部分：一是低频运动；另一个是在低频运动基础上的波频振荡运动。低频运动位置称为瞬时平均位置，而在此平均位置进行波频振荡的运动需要通过摄动展开计算得到。此时，这个摄动展开的参数可以满足小振幅的基本假设。由于此瞬时平均位置需要通过对总体运动响应进行再次展开获得，故此方法称之为两次展开法。

1 数学模型

1.1坐标系的定义和运动响应的分解

图 1 坐标系及计算域定义Fig.1 Definition sketch of coordinate systems and computation domain

(1)

(2)

H中的元素涉及一阶转动分量的乘积，是二阶量。

对物体由波频引起的运动响应在平均位置进行摄动展开如下，

ξ(t)=εξ(1)(t)+ε2ξ(2)(t)+…

(3)

α(t)=εα(1)(t)+ε2α(2)(t)+…

(4)

式中：上标(1)和(2)分别表示关于波陡ε=kA的一阶和二阶分量。

1.2控制方程和边界条件

由于非线性波浪差频的影响，浮体会发生低频漫漂运动，在大地坐标系下的速度势可以写为

(5)

式中：φc为物体低频运动而使周围流场产生定常扰动速度势，与入射波浪无关，为零阶势；φw为大地坐标系下的波浪速度势，可以按照波陡ε展开为一阶和二阶分量。φc和φw均满足拉普拉斯方程和海底不可渗透边界条件。

(6)

式中：φc为单位速度势。将式(5)代入伯努利方程，

(7)

物体慢漂运动的角频率相对波频运动的角频率是小量，而低频运动速度对时间变化率和速度平方的计算均会出现角频率的平方项，可以忽略。因此，伯努利方程可以近似化简为

(8)

速度势Φ满足瞬时物面边界条件，不可渗透海底条件和动力学及运动学瞬时自由水面条件。将物面边界条件和水面边界条件分别在低频平均位置和静水面做泰勒级数展开，得到一阶和二阶的物面和水面边界条件

(9)

(10)

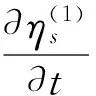
(11)

(12)

(13)

(14)

为了书写简单，式中用Ξ(k)=ξ(k)+α(k)×(x-x0) 表示k阶平移和转动的联合运动。

上述部分为两次展开方法中的第一次展开，即基于低频平均位置做关于未知量的摄动展开和关于边界条件的泰勒级数展开，不同于以往在初始平衡位置展开。本文推导过程考虑了物体做低频大幅慢漂运动的影响，因此和基于初始平衡位置的摄动展开方法相比有根本的不同。

1.3积分方程和波浪力

波浪的散射势和低频运动产生的定常扰动单位速度势均需要通过求解积分方程得到，对于波浪散射势φs，选取Rankine源和它关于海底的镜像作为格林函数：

(15)

式中：R=[(x-x0)2+(y-y0)2+(z-z0)2]1/2,R1=[(x-x0)2+(y-y0)2+(z+z0+2d)2]1/2,x0(x0,y0,z0) 和x(x,y,z)分别表示源点坐标和场点坐标。

利用格林第二定理，可以得到关于计算域边界上速度势的边界积分方程：

(16)

边界S包括淹没于水中的物体表面SB和从物体到阻尼层外边界的有限静水面SF。

而对于定常扰动的单位速度势φc，同样可以利用格林第二定理建立物体表面的积分方程来计算其物面上的速度势。

(17)

自由水面各点的速度势φc同样通过式(17)求得，固角系数选取为1.0。在式(17)中，格林函数为

(18)

其中:

(19)

通过积分方程求出速度势函数以后，作用在瞬时物体湿表面上的压力可以通过Taylor级数展开变换到低频平均物体表面上来表示。按照ε进行分离，力的分量可以按照不同的阶数分解为：

(20)

一阶项波浪力的具体表达式为:

(21)

(22)

二阶项可以表达为

(23)

(24)

(25)

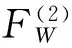
(26)

(27)

1.4低频平均位置计算

根据动量守恒定理，可以分别得到浮体一阶和二阶运动方程

(28)

(29)

式中：[M]为质量矩阵,[B]为粘性阻尼矩阵,[C]为恢复力矩阵,xc=(xc,yc,zc)是物体的质心。E的表达式为:

(30)

为了得到更准确的描述浮体大幅慢漂运动的结果，本文提出的两次展开方法中的第一次展开需要在每一时刻的平均位置进行。为此，平均位置的获得在本方法中显得至关重要。根据模拟得到的运动响应的时间序列，使用小波变换方法找到其平均位置[18]。

结构物在大地坐标系下运动响应的时间序列为χ(nΔt)=(χ1,χ2)，小波函数为Ψ0(η)。计算在纵荡和横荡两个方向分别进行，取任意一个方向为例，对于离散序列的连续小波变换可以定义为具有某一尺度的χ(nΔt)和Ψ0(η)转换形式的卷积

(31)

(32)

为了和连续小波变换近似，式(31)需要对任意一个尺度做N次卷积，其中N为时间序列点的个数。通过卷积定理，上式可转换为χ(t)和ψ*傅里叶变换乘积的逆傅里叶变换：

(33)

(34)

再对连续小波变换进行逆变换，即可得到原始的时间序列

(35)

式中:Cδ为重构系数，为0.776;ψ0(0)为π-1/4。上述部分为两次展开方法中的第二次展开，通过这次数值展开求得低频平均位置，以此作为下一步计算的摄动展开和泰勒级数展开的平均位置。

由于物体表面网格和自由水面网格跟随物体一起做水平慢漂运动，当物体和水面网格移动到新位置时，当前位置的自由水面的速度势和波面高度需要依据前一时刻的结果进行计算。同时，因为网格整体平移，不存在网格变形和拓扑结构的改变，本文采用泰勒展开的方法对当前网格上的速度势和波面高度进行插值计算。

(36)

式中：f表示自由水面各节点的散射势φs和波面高度ηs。当波浪非线性较强的时候，水线上的点由于波面变化较大而不利于数值稳定，本文利用五点光滑法对节点的波面和速度势进行光滑。

2 算例分析与讨论

应用两次展开方法，本文计算了截断圆柱在双色波作用下的大幅慢漂运动。计算结果与基于初始平衡位置的摄动展开方法进行比较，后文称之为直接展开法。文章中选取双色波的差频与系统的自振频率较为接近，以激发圆柱大幅慢漂运动。

圆柱半径a=1.0 m，吃水T=2.5 m，计算水深H=10.0 m。结构只在水平方向施加k11=1 300 N/m的线刚度，此时结构在水平方向的自振频率ω0约为0.3 rad/s。而对于这一系列双色波，波幅均为0.2 m，角频率的和频为6.0 rad/s，沿着x轴正向传播，不同之处是每组波浪的差频不同，具体参数如表 1所示。

表 1 双色波参数Tab.1 Parameters of bichromatic waves

对不同Δω下的二阶运动响应进行傅里叶变换得到不同波浪差频下的二阶运动响应幅值谱，如图 2所示，选取其中几个工况下的二阶运动响应对比分别展示结果，图 3为Δω=0.20 和0.25 rad/s时二阶运动响应的对比，图 4为Δω=0.35 和0.40 rad/s时二阶运动响应的对比。

图 2 不同Δω下二阶纵荡响应傅里叶变换的幅值Fig.2 Fourier transform amplitude of second order surge motion under different Δω

从图 2的结果可以看出，直接展开方法得到二阶运动响应幅值在结构自振频率附近达到最大值，而两次展开方法计算出的二阶运动响应幅值在小于ω0处达到最大。同时，两次展开方法计算出的峰值也小于直接展开方法的峰值。发生这种情况的原因是在两次展开法计算中考虑了物体大幅慢漂运动，结果中包含了波浪漂移阻尼这一项，而这一阻尼项十分重要，无法从直接展开中计算得到。因为波浪漂移阻尼的存在不仅影响了结构的自振频率，同时影响了运动响应的幅值，因此在两次展开法中，结构双色波差频在小于ω0的情况下发生最显著的共振现象。

相应地，系统自振频率的变化影响了不同双色波差频情况下结构物的二阶运动响应。当双色波差频较小时，如图 3所示，即Δω为0.20和0.25 rad/s，比较接近两次展开法得到的系统自振频率，故两次展开法可以计算出更大的二阶运动响应；同理，当双色波差频较大时，如图 4所示，即Δω为0.35和0.40 rad/s，与直接展开法的系统自振频率接近，故二次展开法计算得到的运动响应结果偏小。因此，当结构物发生大幅慢漂运动时，若仍采用直接展开方法计算结构物的运动响应和收到的波浪力，会产生较大的误差。

图 3 二阶纵荡运动响应对比的时间历程线Fig.3 Time histories of second-order surge displacement

图 4 二阶运动响应对比的时间历程线Fig.4 Time histories of second-order surge displacement

3 结 语

本文采用两次展开的方法来求解非线性波浪作用下结构物慢漂运动。在两次展开方法中，物体运动由低频慢漂运动和波频振荡运动组成。速度势分解成波浪引起的一阶、二阶速度势和物体低频运动产生的零阶速度势。波浪引起的各分量根据波陡进行摄动展开，而物面边界条件和水面边界条件在低频运动的平均物面和静水面上采用泰勒级数展开求得，分别建立积分方程来求解波浪的散射势和物体低频运动产生的速度势。初始条件采用二阶Stokes波浪场，自由水面条件的时间积分采用四阶预报校正的方法，浮体的运动方程求解采用Newmark-β法。求得运动响应结果后使用小波变换的数值方法再次展开得到下一时刻摄动展开计算需要的平均位置。

采用本文提出的两次展开方法计算结构物在波浪中发生大幅运动时的波浪力和运动响应，计算结果与基于初始平衡平均位置的摄动展开方法相比有较大区别。文章计算了双色波与截断圆柱的耦合作用，比较了两种方法计算产生的二阶运动响应，从结果可以发现两次展开方法考虑了摄动展开位置随着低频运动的变化，计算结果中包括了波浪慢漂阻尼的部分，使得结构的自振频率向低频偏移，结构的最大响应峰值也低于基于初始平衡位置的直接展开方法的结果。通过波浪与结构物的耦合作用计算，发现两次展开方法不仅可以计算出波浪的结构物遭遇频率的变化，还可以计算出物体大幅慢漂运动时产生的波浪漂移阻尼部分。因此，本位提出的两次展开方法，可以用于深海中平台在大幅慢漂问题的时域计算。

[1] NOSSEN J,GRUE J,PALM E.Wave-forces on 3-dimensional floating bodies with small forward speed [J].Journal of Fluid Mechanics，1991,227：135-160.

[2] KINOSHITA T,BAO W.Hydrodynamic forces acting on a circular cylinder oscillating in waves and small current [J].Journal of Marine Science and Technology,1996,1：155-173.

[3] KINOSHITA T,BAO W,SUNAHARA S.The hydrodynamic forces acting on a cylinder array oscillating in waves and current[J].Journal of Marine Science and Technology,1997,2：135-147.

[4] KIM Y,KIM K H,KIM Y.Springing analysis of a seagoing vessel using fully coupled BEM-FEM in the time domain [J].Ocean Engineering,2009,36(11)：785-796.

[5] LIU Z,TENG B,NING D Z,et al.Wave-current interactions with three-dimensional floating bodies [J].Journal of Hydrodynamics,2010,22(2)：229-240.

[6] SARKAR A,EATOCK TAYLOR R.Low-frequency responses of non-linearly moored vessels in random waves：development of a two-scale perturbation method [J].Applied Ocean Research,1998,20(4)：225-236.

[7] SARKER A,EATOCK TAYLOR R.Low-frequency responses of non-linearly moord vessels in random waves：coupled surge,pitch and heave motions [J].Jounal of Fluids and Structures,2001,15：133-150.

[8] ORMBERG H,LARSEN K.Coupled analysis of floater motion and mooring dynamics for a turret-moored ship [J].Applied Ocean Research，1998,20(1-2)：55-67.

[9] KIM M H,KOO B,MERCIER RM,et al.Vessel/mooring/riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment [J].Ocean Engineering,2005,32(14-15)：1 780-1 802.

[10] TAHAR A,KIM M H.Coupled-dynamic analysis of floating structures with polyester mooring lines [J].Ocean Engineering,2008,35(17-18)：1 676-1 685.

[11] GARRETT D L.Coupled analysis of floating production systems [J].Ocean Engineering,2005,32(7)：802-816.

[12] LOW Y M,LANGLEY R S.A hybrid time/frequency domain approach for efficient coupled analysis of vessel/ mooring/ riser dynamics [J].Ocean Engineering,2008,35(5-6)：433-446.

[13] LOW Y M.Prediction of extreme response of floating structures using a hybrid time/frequency domain coupled analysis approach [J].Ocean Engineering,2008,36：1 416-1 428.

[14] LOW Y M.Extending a time/frequency domain hybrid method for riser fatigue anaylsis [J].Applied Ocean Research,2011,33：79-87.

[15] KIM B W,HONG G S,JIN H K,et al.Comparison of linear spring and nonlinear FEM methods in dynamic coupled analysis of floating structure and mooring system [J].Journal of Fluids and Structures,2013,42：205-227.

[16] YANG M D,TENG B,NING D Z,et al.Coupled dynamic analysis for wave interaction with a truss spar and its mooring line/riser system in time domain [J].Ocean Engineering,2012,39：72-87.

[17] YANG M D,TENG B,XIAO L F,et al.Full time-domain nonlinear coupled dynamic analysis of a truss spar and its mooring/riser system in irregular wave [J].Science China-Physics Mechanics & Astronomy,2014,57(1)：152-165.

[18] CHRITOPHER T,GILBERT C P.A practical guide to wavelet analysis [J].Bulletin of American Meteorological Society,1998,79(1)：64-78.

Large drift motion of mooring cylinder by applying twice expansion method

JIN Ruijia,TENG Bin,LYU Lin

(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)

P751

A

10.16483/j.issn.1005-9865.2016.05.002

1005-9865(2016)05-0011-09

2015-09-28

国家自然科学基金资助项目(51379032,51490672)；国家973资助项目(2011CB013703)

金瑞佳(1987-)，男，江苏武进人，博士研究生，主要从事波浪对海上建筑物作用研究。E-mail ：492472669@qq.com