防城港某码头工程椭圆形沉箱浮游稳定性研究及应用
◎梁剑红 中交四航局第三工程有限公司
1.工程概况
防城港某10 万吨级码头工程中,椭圆沉箱尺寸为26.0m×13.0m(含趾)×22.7m(长*宽*高),脚趾宽1.5m,纵向设5个舱格,横向设2个舱格,共有4 个弧形舱格和6个矩形舱格,其中弧形舱格尺寸近似为半径5m的1/4圆,矩形舱格尺寸为4.43m×4.45m,沉箱底板厚800mm,外壁厚400mm,隔墙厚300mm,共有10个隔舱。
沉箱在预制场上驳至半潜驳,拖轮拖带半潜驳航行至码头现场,半潜驳在下潜区抛锚定位下潜,沉箱浮游出驳,方驳绞锚拖带沉箱定位安装。施工现场为开阔海域,海上风浪大、潮水急,沉箱安装浮游出驳,故需对该沉箱的浮游稳定性进行计算,以验证其是否需要进行压载才能达到浮游稳定,确保沉箱安全、顺利安装到位。
2.椭圆形沉箱浮游稳定计算
结合图1计算简图中信息来看,椭圆沉箱由矩形段与半圆段共同构成。所以这种结构类型的沉箱的浮游稳定性可以分段进行计算:将半圆段的浮游稳定值与矩形段的浮游稳定值进行叠加即为整个椭圆形沉箱的浮游稳定值。
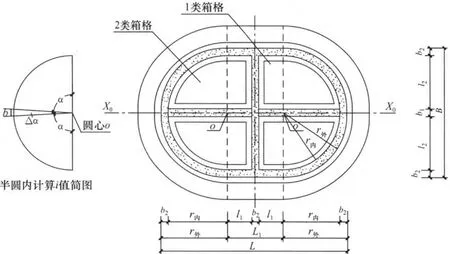
图1 椭圆形沉箱及“i”值计算简图
注:
(1)图1尺寸关系:
b—沉箱内隔墙厚度;b—沉箱外壁厚度;
l—矩形段箱格纵向净长;l—矩形段箱格横向净宽。
(2)计算简图尺寸关系:b—半圆段内侧简化弦长;r—半圆段的边长;
△α—小扇形圆心角。
矩形沉箱浮游稳定计算中定倾半径的计算式可适用于椭圆沉箱:
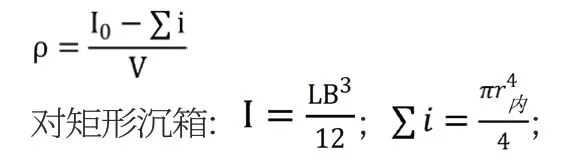
以上表达式中:ρ—沉箱定倾半径(单位:m);I—沉箱断面在水面处对纵向形心轴的惯性矩(单位:m);i—第i箱格内压载水的水面对该水面纵向中心轴的惯性矩(单位:m);Σi—各箱格内压载水的水面对该水面纵向中心轴的惯性矩之和(单位:m);V——沉箱的排水量(单位:m);L—矩形沉箱长度(单位:m);B—矩形沉箱在水面部位的宽度(单位:m);l——矩形沉箱第i箱格纵向墙之间的距离(单位:m);L—第i箱格横向墙之间的间距(单位:m);r—圆形沉箱的外侧半径(单位:m);r—圆形沉箱的内侧半径(单位:m)。
在计算椭圆形沉箱的浮游稳定数值时,其关键是如何计算出Σi值,本文中将对该关键点进行详细的介绍。
2.1 椭圆沉箱定倾半径通式中I0的计算
结合图1可以发现,沉箱断面部位对纵向方向的形心轴的惯性矩总数值为I,为矩形段惯性矩和半圆段惯性矩的叠加,计算表达式为:

2.2 椭圆沉箱定倾半径通式中Σi的计算
结合上文可以知,椭圆形沉箱细分为两个具体的部分:矩形段与半圆段,分别计算其压载水的水面对该水面纵向中心轴的惯性矩之和。
矩形段的Σi:
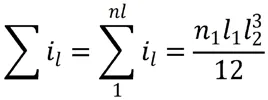
以上表达式中:n——是指矩形段沉箱箱格数,取值为:n=6。
半圆形沉箱可以按照整圆的方式来计算惯性矩,具体的计算以“扇形箱格之圆形沉箱浮游稳定的计算法”作为依据,本文不对其作过多的介绍。
圆形沉箱的2类箱格的内壁视为弦长为b,圆心角为△α的小扇形;扇形箱格自身边长为r,圆心角均为α。
小扇形内壁圆心角:

大扇形箱格圆心角:

以上表达式中:n——是指扇形箱格数,取值为:n=4。
大扇形将y-y轴视为形心轴的惯性矩(单位为:m),x-x、y-y轴分别对应:
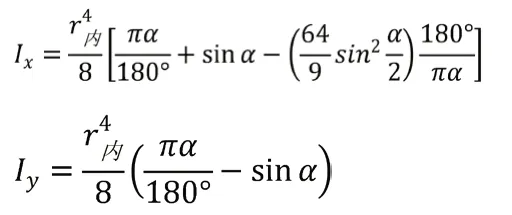
半圆段箱格的水面形心轴(x-x)平行的形心轴惯性矩总和为Σi(m)
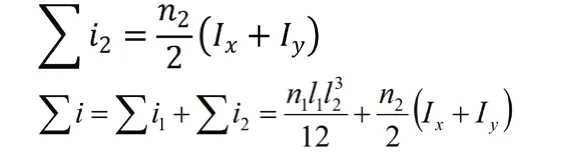
2.3 椭圆沉箱体积和体积矩计算
椭圆形沉箱设计为对称结构,沉箱体积及体积矩计算见表1。

表1 椭圆形沉箱体积及体积矩计算
2.4 椭圆沉箱平衡压载时浮游稳定计算
(1)空载时浮游稳定计算。
空载时椭圆沉箱的重心高度:

空载椭圆沉箱总重
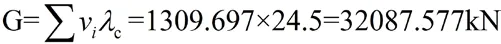
椭圆沉箱总排水体积:

以上表达式中:G—沉箱自重(单位:KN);λ—海水重度,取值为:10.25KN/m;y—椭圆沉箱重心高度(单位:m);λ—混凝土重度,取值为:24.5KN/m;vy—体积矩(单位:m);
沉箱重心在y 轴上,平衡压载时,浮心也在y轴上。因本沉箱前后壁厚度、加强角尺寸相同,均对称布置,故沉箱的重心在沉箱宽度中心线上。
沉箱吃水:
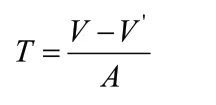
浮心高度:

其中:T为沉箱吃水深度(单位:m);V为沉箱总排水体积(m),V'为沉箱脚趾排水体积(m);A为椭圆沉箱在水面处断面体积(m);y为浮心高度(m)。
沉箱脚趾排水体积V'=V+V=49.350+28.350=77.7m
沉箱吃水:
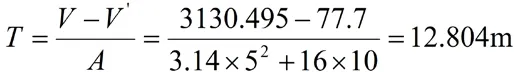
浮心高度:

定倾半径

沉箱重心到浮心的距离:

定倾高度:
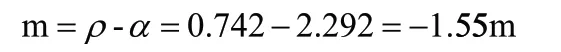
定倾高度m=-1.55m<0.2m,沉箱浮游时不稳定,所以需要加水压载。
(2)根据沿海码头沉箱安装施工经验,假定沉箱压载水为4.5m,计算其浮游稳定性。详见表2。

表2 沉箱压载水为4.5m时重力及重力矩计算表
沉箱总排水体积:

沉箱脚趾排水体积V'=V+V=28.350+49.35=77.7m
沉箱吃水:
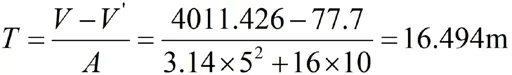
浮心高度:

沉箱重心到浮心的距离α=7.341-8.099-=-0.758m
定倾高度m=ρ -α=0.775-(-0.758)=1.533m
所有沉箱舱格加载4.5m水后,定倾高度m=1.5323m>0.2m,沉箱浮游稳定。
(3)沉箱干弦高度计算
为保证沉箱浮游、拖运及沉放不没顶,应有足够的干舷高度,满足下列公式:
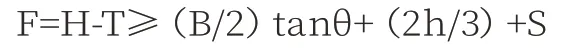
式中:
F——沉箱干舷高度(m);
H——沉箱高度(m),22.7m;
θ——沉箱的倾斜角度,浮运时取6°~8°,取8°;
B——沉箱宽度;
h——为波高,取1m;
S——沉箱干舷富裕高度,一般取0.5~1m。
(B/2 )tan θ+(2 h/3)+S=(26/2)tan 8°+(2×1/3)+1=5.320m
沉箱最小干舷高度为5.320m,
沉箱浮游稳定时吃水T=16.494m,
沉箱浮游稳定时干舷高度F=HT=22.7-16.494=6.206m>5.320m,满足最小干舷高度要求。
2.5 沉箱安装施工方案的选定
经过以上计算,通过椭圆沉箱经过矩形仓格和扇形仓格的叠加计算沉箱的浮游稳定性,通过压载水可使椭圆沉箱达到浮游稳定,选用可满足沉箱安装时的下潜深度等参数要求的半潜驳进行沉箱安装,该安装方案可行。
3.结语
重力式沉箱码头沉箱重力墩式码头是外海开敞式码头的主要结构型式之一,在基岩面较高的地区,几乎是唯一的结构型式。根据沉箱平面形式可分为矩形和圆形两种:矩形沉箱优势是制作简单,浮游稳定性好,但多用于岸壁式码头;圆形沉箱结构对水流阻力小,多用于墩式码头。重力式码头结构以往多数采用圆沉箱结构,2个圆沉箱之间往往造成不均匀沉降。而独立墩式椭圆形沉箱结构码头集矩形和圆形沉箱两大优点:就独立墩而言,椭圆形沉箱较圆形沉箱数量少,可有效节约成本造价;椭圆形沉箱较圆形沉箱与基床接触面积大,可有效扩散码头上部结构应力及外力,以减少地基应力和码头沉降量,同时减少两个圆形沉箱的不均匀沉降;椭圆形沉箱比矩形沉箱受波浪力小,利于重力式码头整体结构稳定。但椭圆形沉箱结构基础码头极为少见,施工经验相对匮乏,施工难度高,特别是安装方面风险高。
综上所述,由于椭圆形的沉箱结构设计比较复杂,加之现有的参考文献对沉箱的浮游稳定计算标准介绍比较模糊,促使沉箱浮游稳定计算趋向于复杂化。但是若将椭圆形沉箱细分为多个部分,则可以有效的解决椭圆形沉箱浮游稳定计算难度比较大的问题。本文通过对椭圆沉箱进行分解、叠加计算其浮游稳定性并成功应用在防城港某码头工程中,为推广大型椭圆沉箱的应用提供切实可行的依据,为同行从业者提供一定的参考价值。

