基于尾缘分离模型的风力机独立变桨性能优化

张蕴宁，　叶　舟, 2，　李　春, 2

(1. 上海理工大学 能源与动力工程学院, 上海 200093；2. 上海市动力工程多相流动与传热重点实验室, 上海 200093)



基于尾缘分离模型的风力机独立变桨性能优化

张蕴宁1，叶舟1, 2，李春1, 2

(1. 上海理工大学 能源与动力工程学院, 上海 200093；2. 上海市动力工程多相流动与传热重点实验室, 上海 200093)

为准确研究风力机高风速非定常气动特性，以NREL Phase VI实验叶片为算例，考虑三维旋转效应和尾缘流动分离现象，建立了Du-Selig三维失速延迟模型与Kirchhoff-Helmholz尾缘分离预估模型耦合的三维尾缘分离预估模型，并与升力面自由涡尾迹法结合,分析了叶片升力面弦向不同涡格数对模拟准确性的影响；基于尾缘分离因子的周向分布规律，通过独立变桨引入风轮旋转半周期的正弦波桨距角增量，抵消相对来流速度变化引起的攻角增大，以优化风力机气动性能.结果表明：升力面弦向采用2涡格的三维尾缘分离预估模型来模拟叶片法向力系数和弦向力系数最为精确；在每个旋转周期内，叶片尾缘分离因子在180°～360°方位角内较大，且在270°达到最大；经独立变桨后，尾缘分离因子得到减小，减小幅度与变桨幅值成正比，且变桨幅值为5°时，叶片主轴扭矩和挥舞力矩达到最佳优化效果.

水平轴风力机； 自由涡尾迹； 尾缘分离； 失速延迟； 独立变桨

近年来，风力机呈现大型化、深海化和智能化的发展趋势[1].风力机工作在非常复杂的三维非定常状态，旋转过程中受到周期性载荷，产生气弹不稳定性，造成风力机的疲劳载荷以及风场中尾流的相互干扰效应，对风力机的性能预测和优化设计提出了更高的要求[2-4]，建立准确的气动模型是其根本前提.在风力机的气动计算模型中，涡尾迹法[5-6]计算精度高于动量叶素理论[7]，效率优于基于各类湍流模型的CFD方法，可准确用于计算低速不可压缩流动[8].笔者采用的自由涡尾迹法可模拟风力机尾迹的相互干扰和畸变等现象[9].

笔者采用时间步进的自由涡尾迹法，为考虑三维旋转特性下叶片尾缘流动分离，模拟并优化高风速偏航工况下的非定常气动特性，建立了Du-Selig三维失速延迟模型[10]与Kirchhoff-Helmholz尾缘分离预估模型[11]耦合的三维尾缘分离预估模型.由于涡尾迹法基于不可压势流理论，物面边界方程认为叶片表面流动不发生分离，适用于低风速工况.而对于高风速工况，叶片尾缘流动已发生分离，因此需对原物面边界方程进行相应修改，引入分离角偏转矩阵以满足尾缘流动分离，在此基础上分别计算升力面不同涡格数对气动性能的影响，并与试验对比得到最佳涡格数布置.

基于尾缘分离因子沿周向分布规律，采用独立变桨技术对风力机叶片在高风速偏航工况下的气动性能进行优化.通过引入风轮旋转半周期的正弦波桨距角增量，抵消相对来流速度变化引起的攻角增大，以减小尾缘分离因子.分析不同的变桨幅值对尾缘分离因子、平均主轴扭矩和挥舞力矩的影响，以得到最优变桨幅值.

1　Du-Selig三维失速延迟模型

许波峰等[12]通过对比6种三维失速延迟模型，得出Du-Selig模型的结果与实验值吻合最好.Du-Selig模型为Du和Selig通过在二维翼型升、阻力系数上添加一个增量提出的升、阻力系数的三维失速延迟模型：

(1)

(2)

式中：Cl,3D、Cd,3D分别为三维升、阻力系数；Cl,2D、Cd,2D分别为二维升、阻力系数；α0为零升力攻角；α为实际攻角；Cd,0为二维零攻角阻力系数；f1、fd为经验修正系数.

经验修正系数fl、fd通过下式求出：

(3)

(4)

式中：c、r和λ分别为当地弦长、当地半径和尖速比；R为叶片半径.

经验修正因子的a、b和d的计算式为

(5)

以美国国家能源部可再生能源实验室(NREL)的 Phase VI实验叶片[13]为算例，以俄亥俄州立大学(OSU)在雷诺数Re=106下所测S809翼型的二维升、阻力系数实验数据为基础，在风速V=10 m/s，风轮转速Ω=1.2 r/s工况下，通过式(1)和式(2)计算经过Du-Selig三维失速延迟模型修正后，叶片各径向位置处升、阻力系数与攻角的对应关系，如图1所示.图中选取了3个径向位置，叶片无量纲半径分别为0.3、0.47和0.8.

由图1可知，Du-Selig三维失速延迟模型对小攻角线性增长区几乎无影响，而对于大攻角失速区，从叶根到叶尖，三维失速延迟模型的修正效果依次减弱.对于r/R=0.3，在大攻角失速区，升力系数几乎随攻角的增大一直保持增长趋势，但阻力系数相对原二维翼型阻力系数减小很多，说明叶片尾缘分离得到很大程度的推移；在r/R=0.8接近叶尖处，经三维失速延迟模型修正后的升、阻力系数与二维实验数据几乎一致，说明叶尖处径向流动效果明显减弱，几乎不造成尾缘分离点的推移.

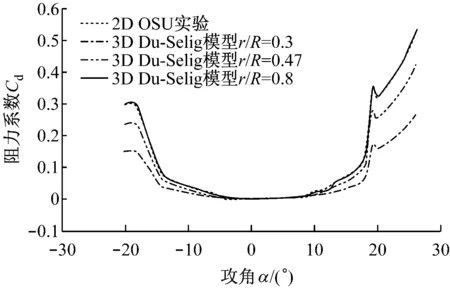
(b) 修正后的阻力系数图1　经Du-Selig三维失速延迟模型修正后的升、阻力系数Fig.1　Lift and drag coefficient corrected by 3D Du-Selig model

2　三维尾缘分离预估模型

笔者将Kirchhoff-Helmholz尾缘分离预估模型[11]与Du-Selig三维失速延迟模型耦合，分析三维旋转情况下叶片径向流动对尾缘分离点位置的影响.图2描述了翼型尾缘流动发生分离时流场结构图，假设分离点距尾缘的距离为x，则定义尾缘分离因子f为x与弦长c的比值，即f=x/c.

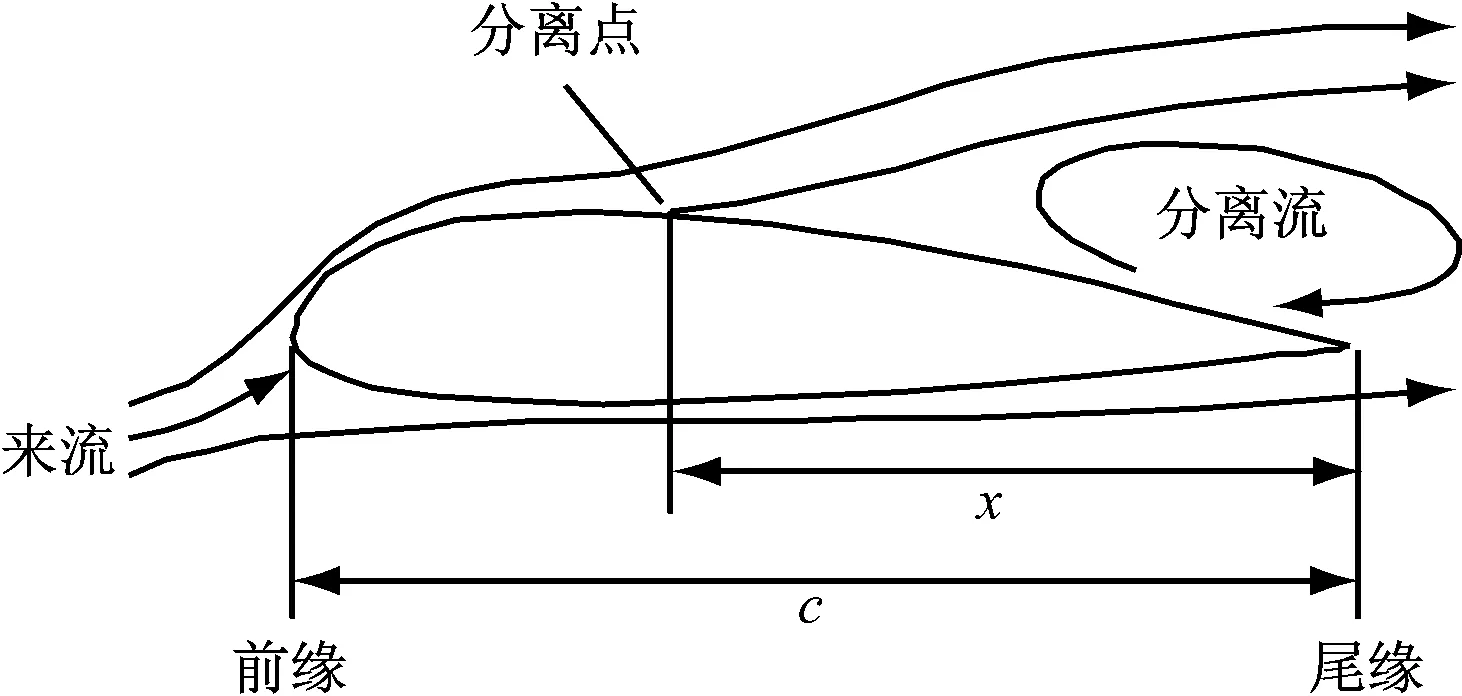
图2　翼型尾缘流动分离示意图Fig.2　Trailing edge flow separation of airfoil

原始的Kirchhoff-Helmholz模型基于二维翼型气动力系数，尾缘分离因子表示为二维法向力系数Cn,2d的函数：

(6)

式中：Cn,0为对应法向力系数为零处的梯度.

根据Du-Selig模型得到三维法向力系数Cn,3d，将其代替式(6)中的翼型二维法向力系数Cn,2d，得到耦合后考虑三维失速延迟特性的尾缘分离预估模型，称其为三维尾缘分离预估模型.

通过式(6)计算二维Kirchhoff-Helmholz模型及耦合后的三维尾缘分离预估模型尾缘分离因子随攻角的变化规律，并与二维翼型风洞实验数据[14]进行对比，结果如图3所示.

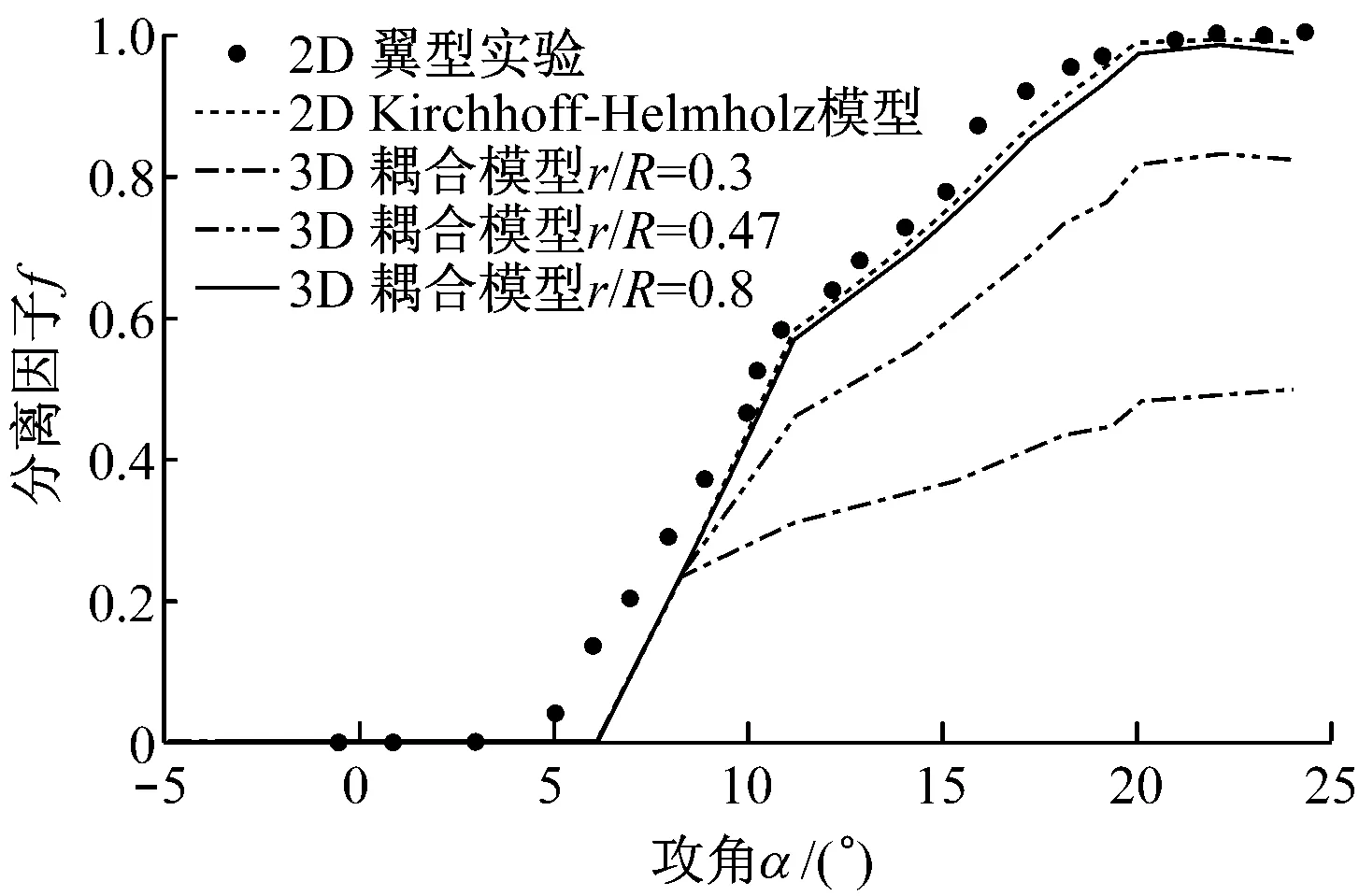
图3　尾缘分离因子随攻角的变化Fig.3　Separation factor vs. attack angle by different prediction models

由图3可知，二维Kirchhoff-Helmholz模型尾缘分离因子与实验值非常接近，说明该模型可准确模拟二维翼型尾缘分离点位置.而耦合后的三维尾缘分离预估模型在不同径向处的尾缘分离因子与二维Kirchhoff-Helmhdz模型各不相同，表明实际三维旋转效应使叶片各径向位置的尾缘分离有不同程度的推移.在r/R=0.3处，尾缘分离因子增大幅度很小，因为叶片径向流动引起失速延迟，分离点推移较明显.在r/R=0.8处，分离点预测几乎与原始二维Kirchhoff-Helmhdz模型一样，说明在靠近叶尖处没有发生明显的失速延迟现象.且攻角在-5°～8°时，三维尾缘分离预估模型和二维Kirchhoff-Helmhdz模型的尾缘分离因子相同，因为攻角小于8°时，升、阻力系数处于线性增长区，Du-Selig三维失速延迟模型对升、阻力系数无影响，如图1所示.

3　升力面自由涡尾迹法

自由涡尾迹法通过求解二维Laplace方程得到二维流场中叶片的升力分布：

(7)

式中：φ为速度势函数，且满足▽φ=Vk+Vind；Vk为相对来流合速度；Vind为附着涡和尾迹自由涡对控制点的诱导速度.

为考虑黏性对诱导速度的影响，且避免计算诱导速度时出现奇值，采用Lamb-Ossen涡核模型，并引入时间补偿参数改变涡核起始半径，涡核半径随时间增大的公式如下：

(8)

式中：α为经验系数，取常数1.256 43；v为空气运动黏度；t为时间；Sc为时间补偿参数；δv为扰动黏性系数；根据文献[15]，Sc取值0.1，δv取100.

叶片采用具有环量的升力面模型，经典的Weissinger-L升力面模型用一排涡格代替叶片，在距叶片前缘1/4弦向处布置附着涡，位于气动中心.在距叶片前缘3/4弦向处布置控制点，即涡格中心.笔者采用多涡格升力面模型，从叶片前缘至尾缘，弦向等距划分M个网格，径向划分N个网格，如图4所示.每个网格布置一个涡格，涡格距网格前缘1/4弦向距离，每个涡格的4条涡线具有相同环量值，涡格环量方向根据右手定则与涡格法向量同向.

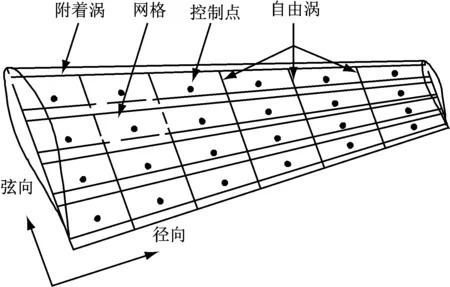
图4　叶片升力面涡格划分Fig.4　Vortex lattice distribution on blade lifting surface

通过满足物面边界方程求解附着涡格环量，笔者在物面边界方程中引入一分离角η，偏转矩阵满足尾缘流动分离，如下式所示：

(9)

式中：n为涡格法向向量.

数值模拟时，计算各径向位置有效攻角，求出图3中各自对应的尾缘分离因子，得到各径向位置尾缘开始分离的涡格，在相应涡格上运用式(9)，在10 m/s风速下取分离角为5°，对未出现分离的涡格，取分离角为0°.

4　计算结果

4.1高风速非定常气动性能模拟

以NREL Phase VI的实验算例为研究对象，叶片长度为5.03 m，桨距角为3°，风轮转速为1.2 r/s，叶片弦长及扭角数据参考文献[13].

模拟高风速10 m/s下，偏航角θyaw为10°和30°的工况，分别用经典的单涡格Weissinger-L升力面模型与基于三维尾缘分离预估模型的多涡格升力面模型预估气动性能，并与实验结果进行对比.图5和图6分别表示各模型计算所得叶片径向法向力系数和弦向力系数.

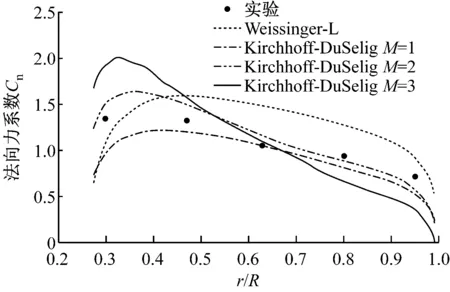
(a) V=10 m/s， θyaw=10°

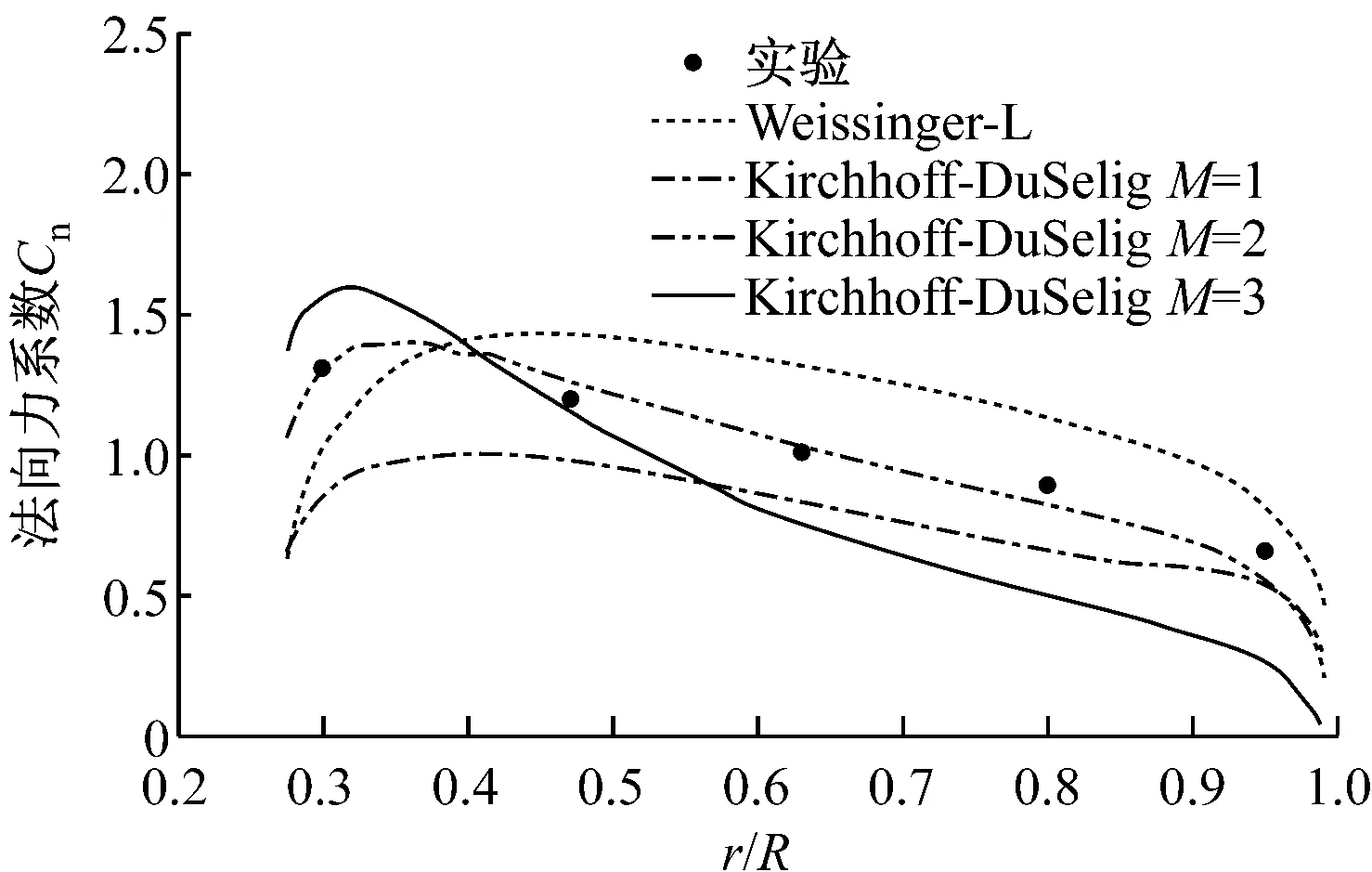
(b) V=10 m/s， θyaw=30°图5　风速10 m/s时不同偏航角下叶片径向法向力系数分布Fig.5　Normal force coefficient of blade at 10 m/s wind speed and different yaw angles

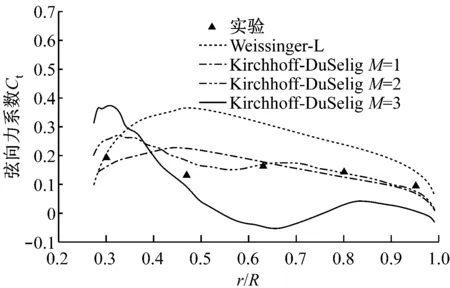
(a) V=10 m/s， θyaw=10°

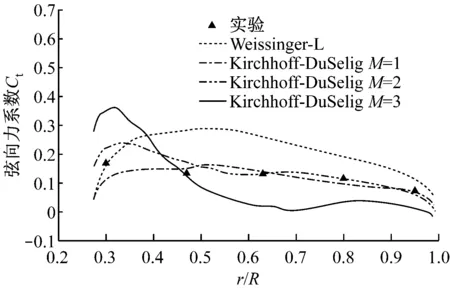
(b) V=10 m/s， θyaw=30°图6　风速10 m/s时不同偏航角下叶片径向弦向力系数分布Fig.6　Tangential force coefficient of blade at 10 m/s wind speed and different yaw angles

图5和图6所示的2种偏航角下，Kirchhoff-DuSelig模型M=2时计算所得气动力系数均与实验值非常吻合.由于Weissinger-L升力面模型仍求解未分离的物面边界方程，导致模拟值明显偏大.对于Kirchhoff-DuSelig模型，M=1时，引入尾缘分离因子后，气动力系数得到有效减小，但是弦向单涡格导致叶片表面分离过早.而Kirchhoff-DuSelig模型M=2时既考虑了由于尾缘分离所引起的气动力系数减小，又适当地增加了涡格数，可以更准确地描述尾缘分离点位置.Kirchhoff-DuSelig模型M=3时，虽然能更准确地描述尾缘分离点位置，但是涡格数增多会引起叶片附着涡诱导速度增大，尤其是轴向诱导速度，导致误差增大.

图7给出了风速10 m/s时，偏航角为10°和30°工况下，4个旋转周期内叶片表面各径向位置尾缘分离因子的周向分布云图.

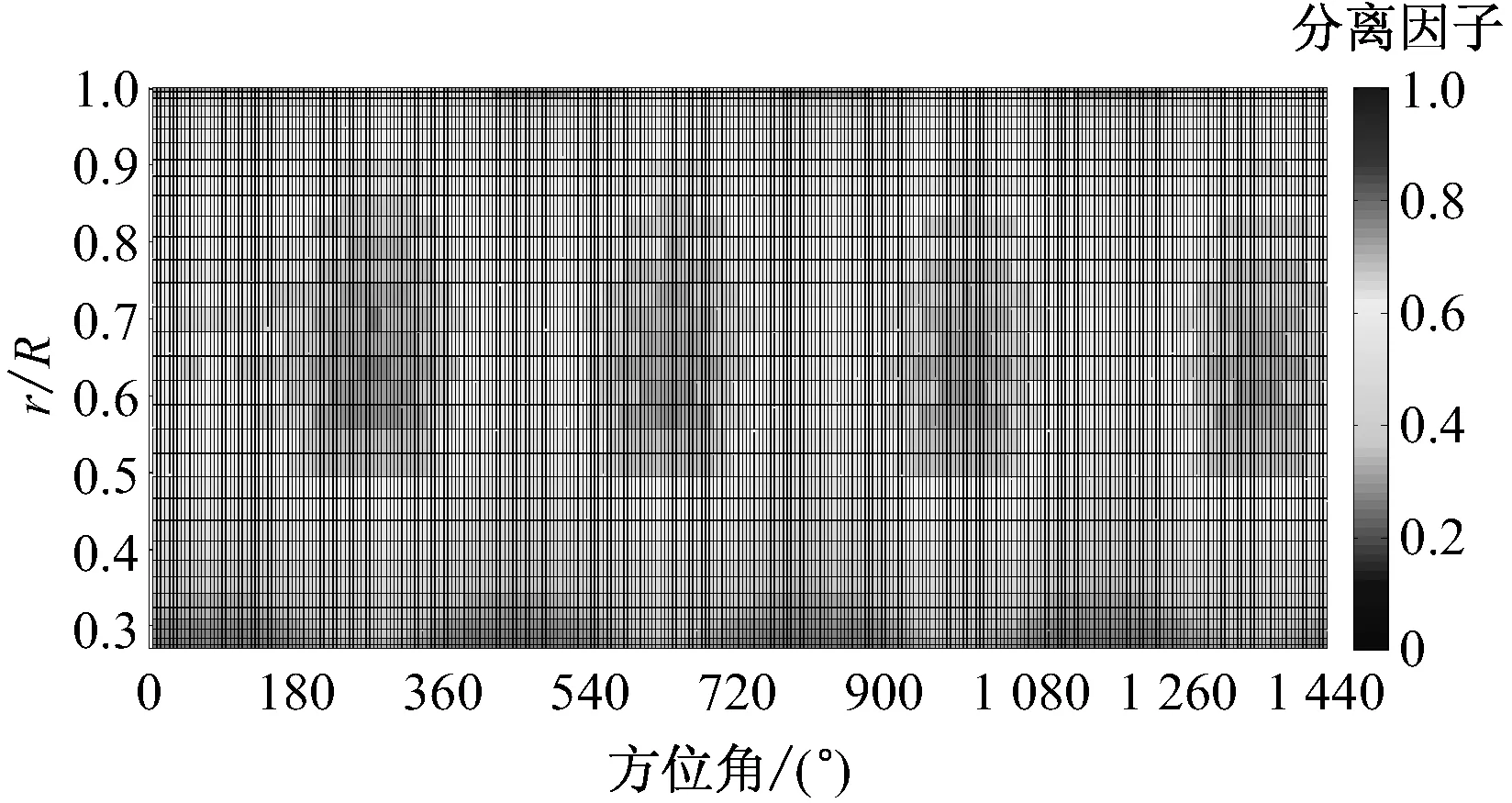
(a) V=10 m/s， θyaw=10°

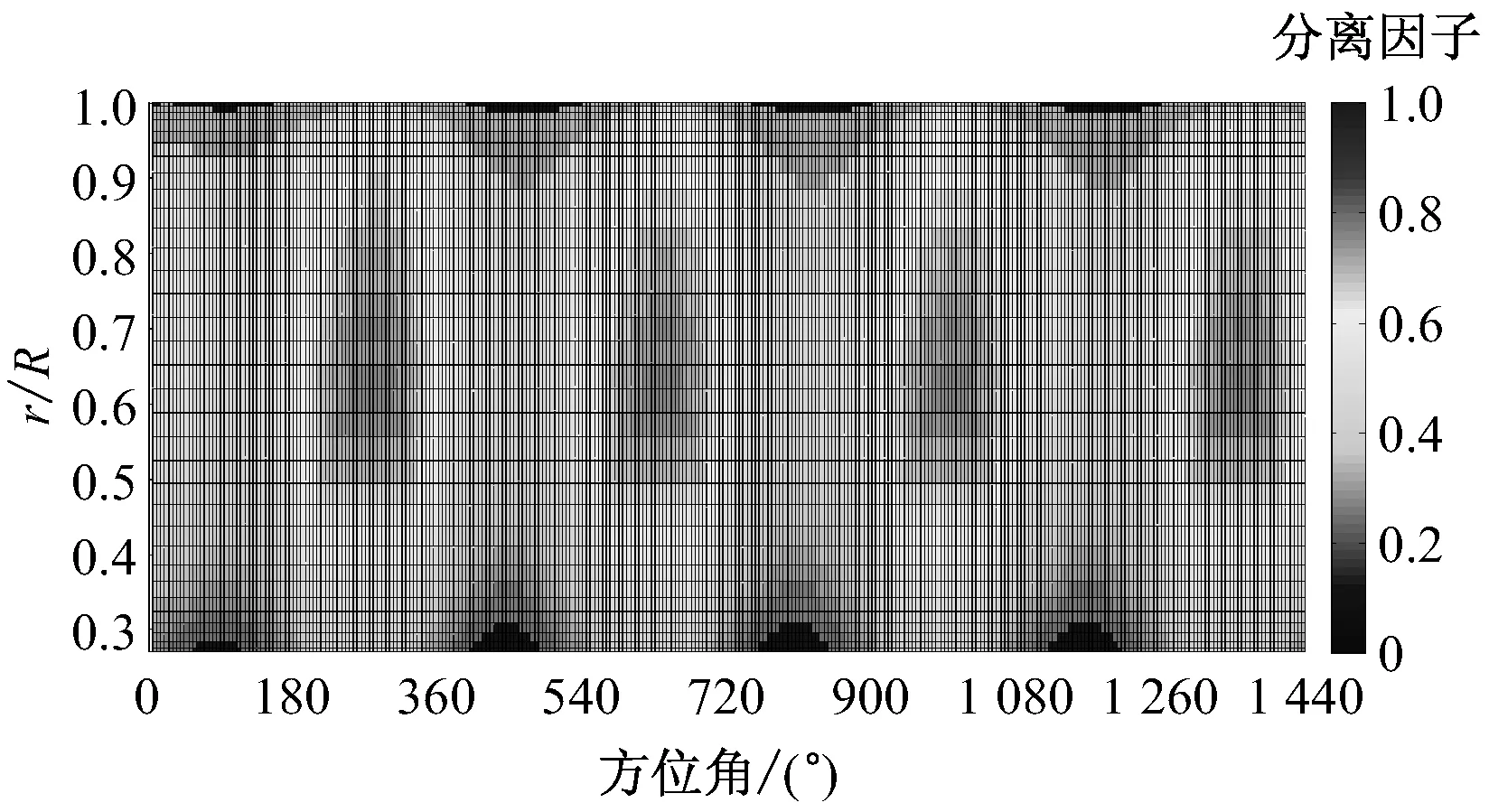
(b) V=10 m/s， θyaw=30°图7　风速10 m/s时不同偏航角下各径向位置尾缘 分离因子的周向分布Fig.7　Circumferential distribution of trailing edge separation factor at 10 m/s wind speed and different yaw angles

由图7可知，各径向位置尾缘分离因子随当地攻角呈周期性变化，在靠近叶根处，由于三维旋转效应引起的失速延迟现象，尾缘分离点后移，分离因子较小；在靠近叶尖处，由于攻角很小，分离因子也较小；在中间叶高处，图3表明失速延迟效应没有近叶根处明显，且攻角较大，因此尾缘分离因子最大.在每个旋转周期内，尾缘分离因子总在90°方位角最小，在270°方位角达到最大，因为在90°方位角，来流速度在x轴的偏航分速度与相对旋转速度同向，造成攻角大幅减小，尾缘分离减弱；而在270°方位角，来流速度在x轴的偏航分速度与相对旋转速度反向，造成攻角大幅增大，尾缘分离加强.

4.2变桨优化

由于尾缘分离因子在旋转周期180°～360°范围内较大，因此通过独立变桨方法，在该区间加入一正弦波动桨距角增量，以抵消相对来流速度变化引起的攻角增大，从而减弱尾缘分离，达到优化气动力矩的目标.桨距角增量θpitch用下式表示：

(10)

式中：ψ为风力机方位角；A为桨距角变桨幅值，直接影响变桨后叶片气动性能.

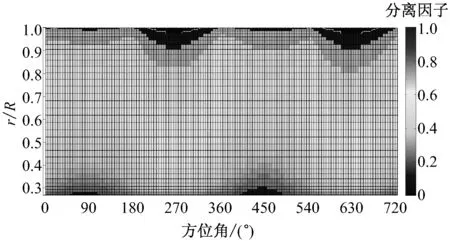
以风速10 m/s、偏航角30°为研究工况.图8给出了原始无变桨和加入变桨后叶片尾缘分离因子在2个旋转周期内的分布情况.由图8可知，随着桨距角变桨幅值增大，180°～360°区间内尾缘分离因子减小更加明显.

变桨幅值A=0°为不加入变桨的原始偏航工况.A=3°时，叶片尾缘分离因子有比较明显的减小，但是中间叶高处的尾缘分离因子依然很大；A=5°时进一步减小了中间叶高处的尾缘分离因子，中间叶高处至叶尖，尾缘分离因子基本减小至0.5以下，而中间叶高处至叶尖提供了绝大部分的叶片扭矩，因此A=5°时叶片扭矩有大幅度提高；A=8°时，虽然叶片径向尾缘分离因子都有大幅度减小，但靠近叶尖部分出现大区域尾缘分离因子为0，说明此时靠近叶尖部分攻角已降为负攻角.由于近叶尖部分提供了叶片大部分扭矩，变桨幅值为8°对气动性能的优化效果不大，甚至可能会减小叶片扭矩.

为分析尾缘分离因子的减小对叶片气动性能的影响，计算变桨后叶片的气动力矩.图9为2个旋转周期内不同桨距角变桨幅值A对应叶片主轴扭矩及挥舞力矩随方位角的变化，将变桨幅值A分别为3°、5°和8°的结果与原始无变桨工况A=0°的数据进行对比.如图9所示，采用独立变桨方法，对于不同的桨距角变桨幅值，在180°～360°方位角变桨区，主轴扭矩均有增大，挥舞力矩均有减小.在非变桨区，气动力矩相对原始无变桨工况几乎不变.

图10给出了每个旋转周期内，变桨区平均主轴扭矩和平均挥舞力矩随变桨幅值的变化.由图10可知，随着变桨幅值的增大，变桨区平均主轴扭矩先增大后减小，在A=5°时达到最大，且关于5°呈左右对称分布.当变桨幅值增至10°左右时，平均主轴扭矩减小至低于原始无变桨工况，说明此时的攻角减小量过大，已超过了原始无变桨工况的失速修正区攻角，叶尖上出现的负攻角对叶片气动性能的降低有主要影响，对应图8(d)中叶尖尾缘分离因子出现大区域的零值.随着变桨幅值的增大，变桨区平均挥舞力矩持续减小.由于笔者采用的是半周期的变桨控制方法，在变桨区，平均挥舞力矩不宜减小太大，否则会造成偏航力矩和俯仰力矩过大.因此，无论从增大主轴扭矩还是减小挥舞力矩的角度，采用半周期变桨幅值为5°的桨距角控制方法可得到最佳的叶片气动性能.

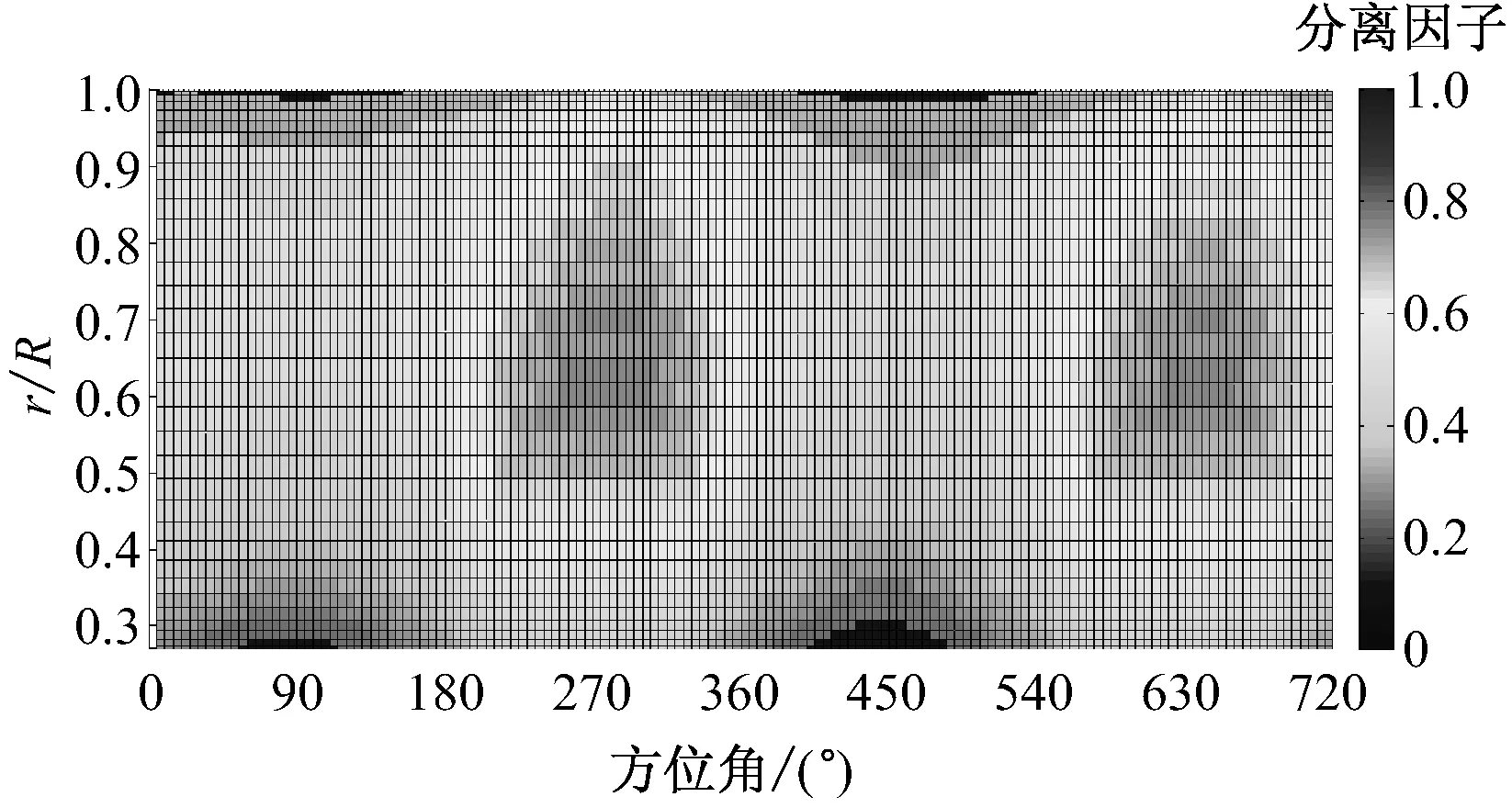
(a) 无变桨工况，变桨幅值A=0°

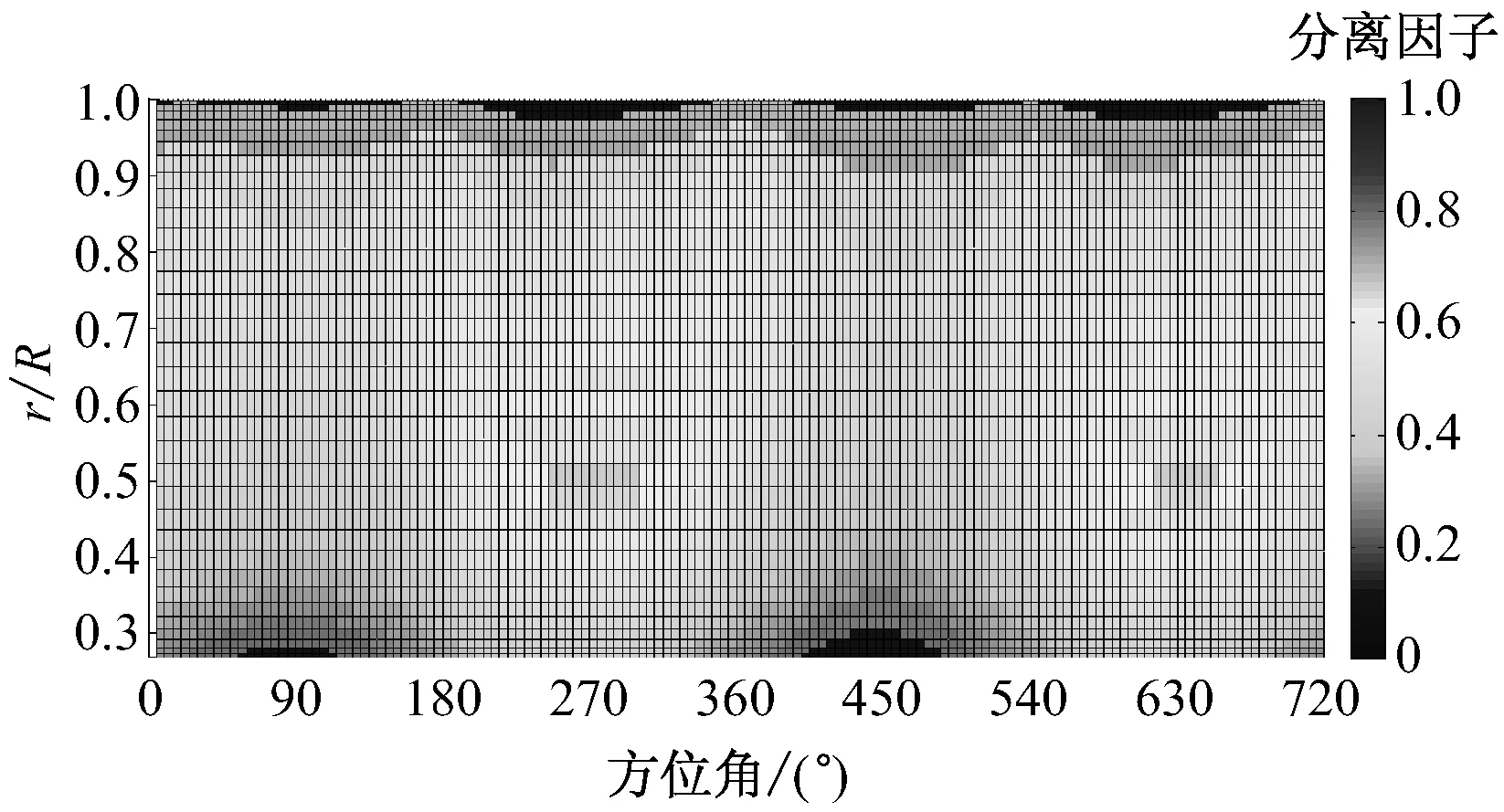
(b) 变桨工况，变桨幅值A=3°

(c) 变桨工况，变桨幅值A=5°

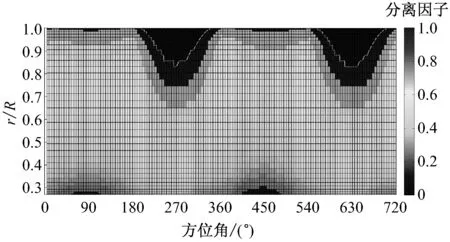
(d) 变桨工况，变桨幅值A=8°图8　不同变桨幅值对尾缘分离因子的影响Fig.8　Trailing edge separation factor vs. pitch amplitude

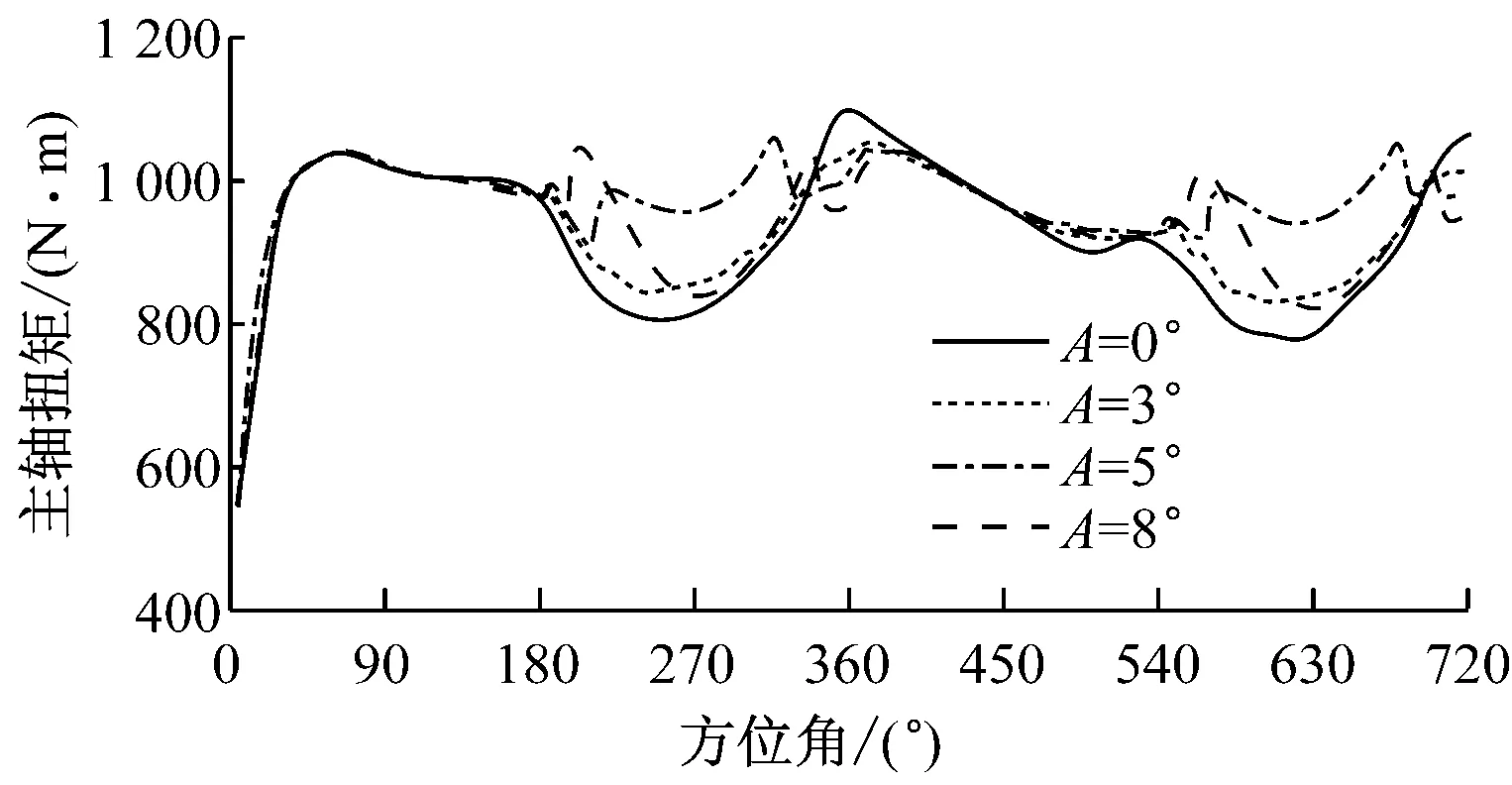
(a) 主轴扭矩

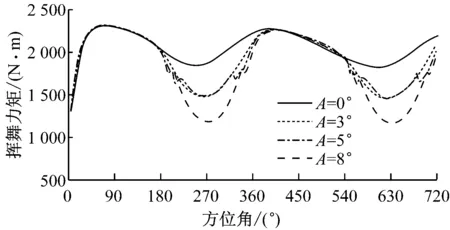
(b) 挥舞力矩图9　不同变桨幅值对主轴扭矩和挥舞力矩的影响Fig.9　Distribution of shaft and flap wise torque at different pitch amplitudes

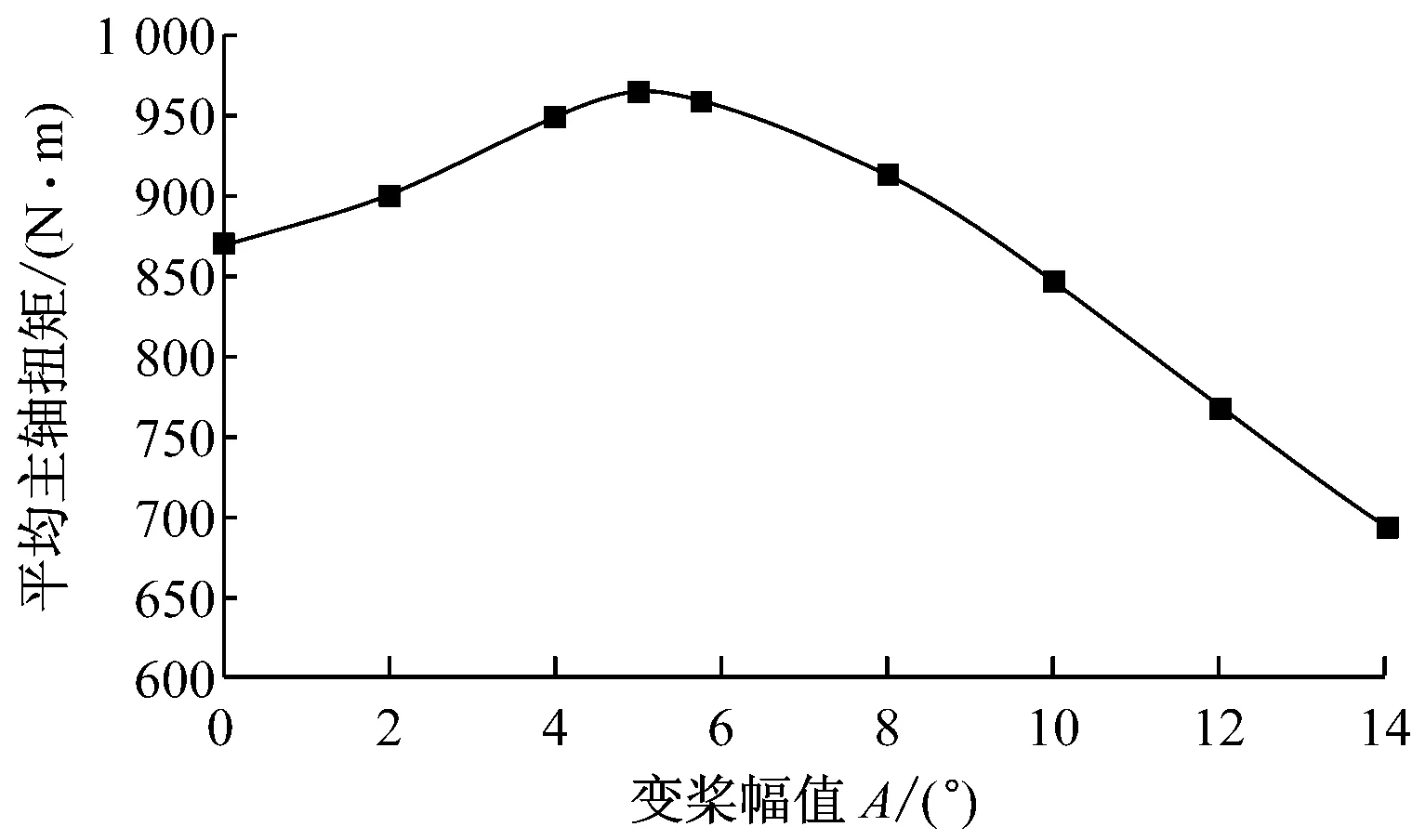
(a) 变桨区平均主轴扭矩

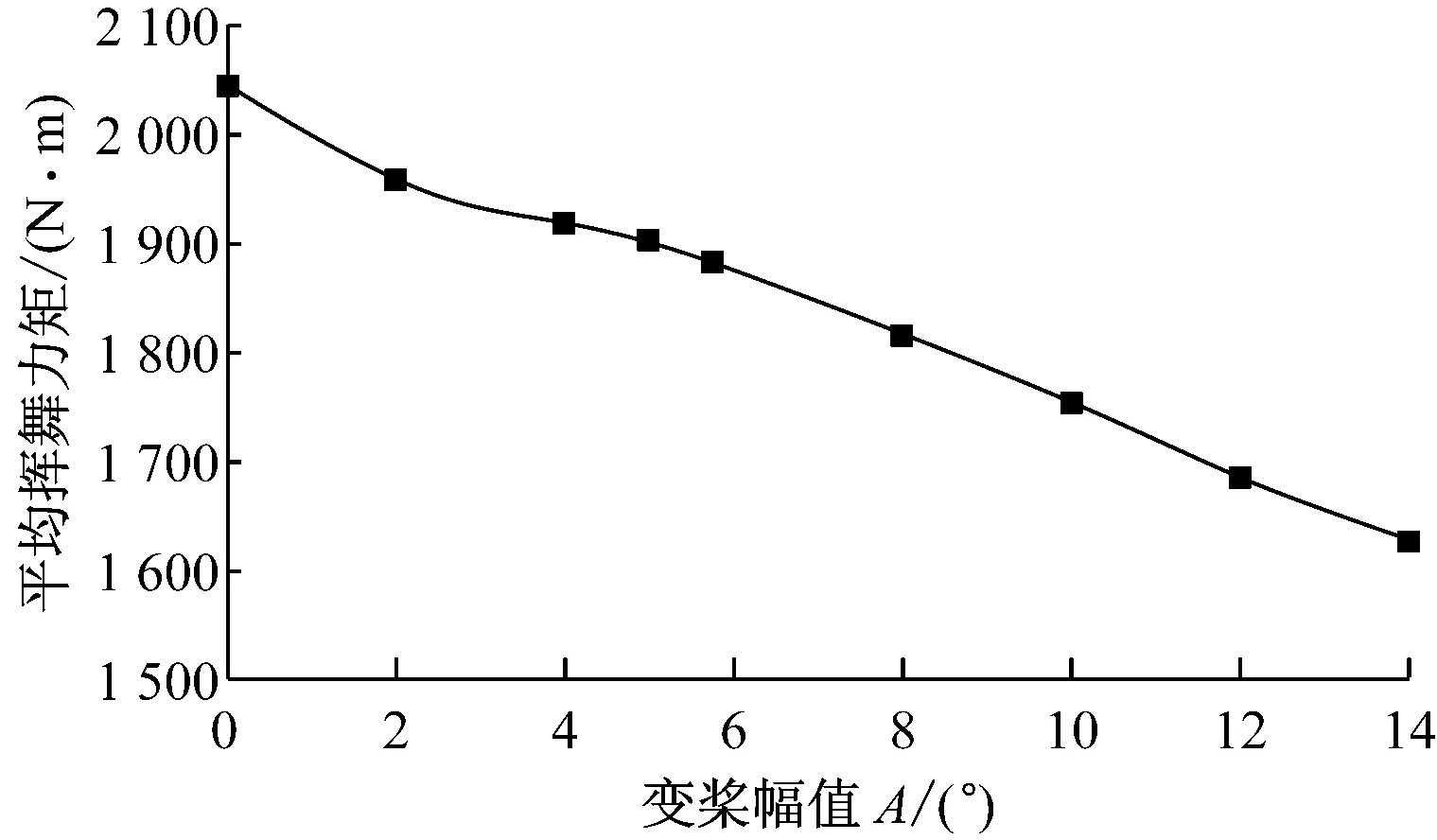
(b) 变桨区平均挥舞力矩图10　不同桨距角变桨幅值对变桨区平均主轴扭矩和平均挥舞力矩的影响Fig.10　Distribution of average shaft and flap wise torque at different pitch amplitudes

5　结　论

(1) 以高风速偏航工况为研究对象，考虑三维旋转效应和尾缘流动分离现象，建立了Kirchhoff-Helmholz尾缘分离预估模型与Du-Selig三维失速延迟模型耦合的三维尾缘分离预估模型.采用2涡格Kirchhoff-DuSelig三维尾缘分离预估模型模拟的气动力系数与实验值最为接近.

(2) 得出风速为10 m/s时不同偏航角下叶片径向分离因子随方位角的变化规律.中间叶高处分离因子较大，且在每个旋转周期内，分离因子在90°方位角最小，在270°方位角最大.

(3) 采用独立变桨方法，对风力机叶片在偏航工况下的气动性能进行优化，通过引入半周期的正弦波桨距角增量来减小尾缘分离因子.随着变桨幅值增大，变桨区平均主轴扭矩先增大后减小，平均挥舞力矩持续减小，在变桨幅值取5°时达到最佳优化效果.

[1]李春，叶舟，高伟，等. 现代大型风力机设计原理[M]. 上海：上海科学技术出版社，2013.

[2]郭强，刘鹏寅，竺晓程. 风力机非定常气动力降阶模型[J]. 动力工程学报，2015, 35(7):588-592.

GUO Qiang, LIU Pengyin, ZHU Xiaocheng. Reduced-order models for unsteady aerodynamic load of wind turbines[J]. Journal of Chinese Society of Power Engineering, 2015, 35(7):588-592.

[3]杨阳，李春，缪维跑，等. 基于多目标遗传算法的风力机叶片全局优化设计[J]. 机械工程学报，2015, 51(6): 45-51.

YANG Yang, LI Chun, MIAO Weipao,etal. Global optimal design of wind turbines blade based on multi-object genetic algorithm[J]. Journal of Mechanical Engineering, 2015, 51(6): 45-51.

[4]唐迪，陆志良，郭同庆. 大型风力机整机气动弹性响应计算[J]. 振动工程学报，2015, 28(1):38-43.

TANG Di, LU Zhiliang, GUO Tongqing. Aeroelastic simulations of a large horizontal-axis wind turbine[J]. Journal of Vibration Engineering, 2015, 28(1):38-43.

[5]KOMNINOS K. Modeling considerations of the optimum rotor using vortex method[D]. Denmark: Technical University of Denmark, 2008.

[6]REUVEN S. Design and optimization of planar and nonplanar wind turbine blades using vortex methods[D]. Denmark: Technical University of Denmark, 2010.

[7]GLAUERT H. An aerodynamic theory of the airscrew[M]. England: Cambridge University Press, 1922:199-220.

[8]沈昕. 水平轴风力机气动性能预测及优化设计[D]. 上海：上海交通大学, 2014.

[9]李少华，王东华，岳巍澎，等. 双风力机风向变化时尾流及阵列数值研究[J]. 动力工程学报，2011, 31(10):768-772.

LI Shaohua, WANG Donghua, YUE Weipeng,etal. Numerical simulation on wake interaction and array of double wind turbine at varying wind directions[J]. Journal of Chinese Society of Power Engineering, 2011, 31(10):768-772.

[10]杜朝辉. 水平轴风力涡轮设计与性能预估方法的三维失速延迟模型——Ⅲ. 模型改进[J]. 太阳能学报, 2000, 21(2):145-150.

DU Zhaohui. A 3-D stall-delay model for HWAT performance prediction: Ⅲ. mode improvement[J]. Acta Energiae Solaris Sinica, 2000, 21(2):145-150.

[11]LEISHMAN J G, BEDDOES T S. A generalised model for airfoil unsteady aerodynamic behaviour and dynamic stall using the indicial method[C]//Proceedings of the 42nd annual forum of the American Helicopter Society. Washington DC, USA：American Helicopter Society, 1986: 243-265.

[12]许波峰，王同光，张震宇. 风力机三维旋转效应模型研究[J]. 太阳能学报，2014, 35(4):562-567.

XU Bofeng, WANG Tongguang, ZHANG Zhenyu. Investigation on three dimensional rotational effect model for wind turbine[J]. Acta Energiae Solaris Sinica, 2014, 35(4):562-567.

[13]SIMMS D A, FINGERSH L J, JAGER D W,etal. Unsteady aerodynamics experiment phase VI: wind tunnel test configurations and available data campaigns[M]. Colorado，USA：National Renewable Energy Laboratory, 2001.

[14]SHENG W, GALBRAITH R A M D, COTON F N. On the S809 airfoil's unsteady aerodynamic characteristics[J]. Wind Energy, 2009, 12(8): 752-767.

[15]SANT T, van KUIK G, van BUSSEL G J W. Estimating the angle of attack from blade pressure measurements on the NREL phase VI rotor using a free wake vortex model: axial conditions[J]. Wind Energy, 2006, 9(6): 549-577.

Wind Turbine Aerodynamic Performance Optimization by Individual Pitch Control Based on Trailing Edge Separation Model

ZHANGYunning1,YEZhou1, 2,LIChun1, 2

(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

To simulate the unsteady aerodynamic performance of a wind turbine with NREL phase VI test blade, a three-dimensional trailing edge separation prediction model was established by coupling the Kirchhoff-Helmholz trailing edge separation prediction model with 3D Du-Selig stall delay model, in consideration of the three-dimensional rotational effect and trailing edge separation phenomenon, while the influence of vortex lattice number on the calculation accuracy was analyzed using lifting surface free vortex wake method. Based on the tangential distribution of separation factor, the wind turbine aerodynamic performance was then optimized by introducing a sin wave pitch increment in half period of rotation through individual pitch control to offset the increase of attack angle resulted by the change of relative inflow velocity. Results show that when the three-dimensional trailing edge separation prediction model with two vortex lattices on the lifting surface is adopted, optimum simulation results of normal and tangential force coefficient would be obtained. In each period of rotation, the trailing edge separation factor is relatively higher between 180° and 360°, which reaches the maximum at 270°. The trailing edge separation factor is reduced by individual pitch control, and the reducing magnitude increases with the rise of pitch angle; both the shaft and flap wise torque would achieve the optimum optimization effect when the pitch angle is set at 5°.

horizontal axis wind turbine; free vortex wake method; trailing edge separation; stall delay; individual pitch control

2015-09-29

2015-11-24

国家自然科学基金资助项目(E51176129)；上海市教育委员会科研创新资助项目(13YZ066)；上海市科委资助项目(13DZ2260900)

张蕴宁(1991-)，女，江苏句容人，硕士研究生，主要从事风力机叶片气动性能方面的研究.电话(Tel．)：13248268931；

E-mail：zyn416@163.com．

1674-7607(2016)09-0739-07

TK83

A学科分类号：470.30