基于偏序关系的粗糙集规则提取方法
陈志恩
(宁夏师范学院数学与计算机科学系,宁夏固原 756000)
基于偏序关系的粗糙集规则提取方法
陈志恩
(宁夏师范学院数学与计算机科学系,宁夏固原756000)
规则提取算法中通常先约简属性再约简属性值,但该算法当属性数量增多时,会增加约简的复杂性,从而影响规则提取的速度.针对此问题,本文提出了一种基于偏序关系的粗糙集规则提取方法.首先,在不同粒度的知识空间上建立偏序关系;然后,利用各知识空间中隐含的属性冗余度作为启发式信息,对冗余属性进行逐层约简;最后,在约简后的属性集上提取决策规则.实例表明,该方法降低了属性约简的复杂性,提高了规则提取的速度.
粗糙集;偏序关系;属性约简;规则提取
0 引言
粗糙集理论[1-2]的一个主要任务是从信息表中获取知识,而这种知识通常用规则的形式表示出来.用粗糙集方法得到决策规则的关键在于属性约简,相对约简和最小约简[2]是属性约简的两个重要结果.求最小约简被证明是NP-hard问题[3].相对约简不一定是最小约简,且它不一定是唯一的.知识约简是规则提取的关键步骤,研究者往往先给出相应的启发式信息,然后设计某种启发式约简算法,在知识空间中按照自顶向下或自底向上的方式实现约简.
从粒计算的角度来看[4-7],属性约简的目的就是在条件属性集中寻找一个属性子集,该子集对论域形成的划分空间是保持正域不变(或条件信息熵不变)前提下粒度最粗的划分空间.不管哪种属性约简方法,其实质就是删除冗余属性,依照不同的属性重要度量方法和原理得到不同的约简结果,从而得到不同的决策规则.Dai等[8]以条件属性子集的分类一致性来度量属性的重要性,当选择的属性子集能正确分类时,获取决策规则;Qian等[9]在研究可辨识矩阵的基础上提出了类别特征矩阵的概念,将原始决策表分成若干个等价子决策表,并借助核属性和属性频率函数对各类别特征矩阵挖掘决策规则;Zhang等[10]从分析属性约简的粒度原理出发,指出传统的规则挖掘方法存在的弊端,并提出了一种基于最大粒的规则获取算法;Chen等[11]将属性约简和属性值约简过程合二为一,以知识粒为单位挖掘规则,先对决策信息系统分层粒化,在不同粒度的知识空间下计算粒关系矩阵,并从中获取启发式信息,然后根据启发式信息确定信息粒的属性值约简顺序,在此基础上去除冗余属性,并设定终止条件,实现决策规则的快速挖掘.但上述各属性约简方法中,当属性集中属性数量增多时,约简复杂性会急剧增加.为此,本文提出一种基于偏序关系的粗糙集规则提取方法.该方法首先在不同粒度的知识空间上建立偏序关系,然后将不同粒层知识空间中隐含的属性冗余程度信息作为启发式算子,在不同粒层的偏序关系集上对冗余属性进行约简;最后,在约简后的属性集上提取决策规则.实例计算结果表明,该方法降低了属性约简的复杂性,提高了规则提取的速度,与传统方法形成了较好的互补.
1 基本概念
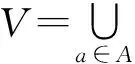
如果A=C∪D且C∩D=∅,D≠∅,C是条件属性集,D是决策属性集,则称该信息系统为决策信息系统,有时也称为决策表.决策信息系统中的每一行代表一条决策规则.
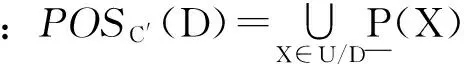
定义1[2]决策信息系统S=(U,A,V,f)中,若C′⊆C,且POSC′(D)=POSC′-{r}(D),则称r为C′中相对于决策属性D可省略的(不必要的),否则,称r为C′中相对于决策属性D不可省略的(必要的),简称r为必要属性.
定义2[2]在决策信息系统S=(U,A,V,f)中,如果C′⊆C,且C′中的每一个r都是C′中相对于决策属性D不可省略的,则称C′为相对于决策属性D独立的,简称C′是独立的.
定义3[2]在决策信息系统S=(U,A,V,f)中,如果P⊆C,且对P的独立子集S(S⊂P),有POSS(D)=POSP(D),则称S为P的相对约简.相对约简可能不唯一,记P的所有相对约简簇为REDD(P),P的所有相对约简中,属性个数最少的称为最小约简.
定义4[2]设S=(U,A,V,f)是决策信息系统,对任意的一个属性集C′⊆C,称划分U/C′为条件划分空间(或条件粒空间),称划分U/D为决策划分空间(或决策粒空间).
定义5[2]设S=(U,A,V,f)是决策信息系统,A=C∪D,如果U/C⊆U/D,则称S为一致决策信息系统.
定义6设S=(U,A,V,f)是决策信息系统,若条件属性C′和决策属性D对论域U的划分为U/C′={X1,…,Xi,…,Xm},1≤i≤m≤l,U/D={Y1,…,Yj,…,Ys},1≤j≤s≤l,则称等价类Xi,Xj为信息粒.记Grad(C′)=U/C′,Grad(D)=U/D,Grad(C′)表示由条件属性C′产生的信息粒,Grad(D)表示由决策属性D产生的信息粒.
定义6表明,每个属性都可形成很多粒子,不同属性形成的粒子可合成新的粒子.在决策信息系统中,若令1≤ω≤n,则ω表征当前系统的粒度,n为条件属性个数.这样系统对应有n种粒度,并且粒度ω越小,表明系统的知识粒度越粗.
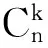
例1设决策信息系统S=(U,A,V,f)中,U={x1,x2,…,x7},条件属性集C={a,b,c,d},决策属性集D={e},如表1所示.
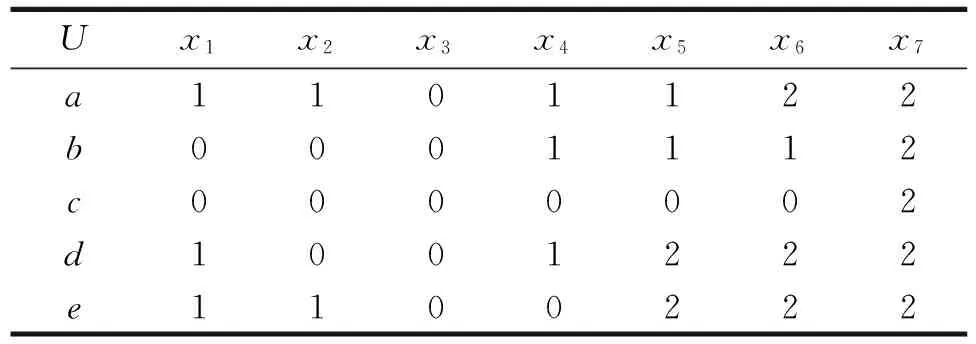
表1 决策信息系统
首先,计算由决策属性集D={e}产生的信息粒Ye={{x1,x2},{x3,x4},{x5,x6,x7}}.
其次,取粒度ω=1,则第1层知识空间{ω=1}={{a},{b},{c},{d}},分别计算该层空间上由单个属性产生的信息粒如下:
取粒度ω=2,则第2层知识空间{ω=2}={{ab},{ac},{ad},{bc},{bd},{cd}},分别计算该层空间上由两个属性合成的信息粒如下:
类似地,可取粒度ω=3及ω=4,分别计算第3层和第4层知识空间上的信息粒.
在决策信息系统S=(U,A,V,f)中,C为条件属性,则代数系统P(C),⊂是由属性空间构成的一个完备格,其中,P(C)表示属性集合C的幂集.按照格的基本原理,C是格中的最大(极大)元,∅是格的最小(极小)元.在格P(C),⊂对应的Hasse图中,从∅到C的一条路径称为属性链.
定义7[12](偏序关系和偏序集)给定非空有限集合X和Y上的一个关系R,若R满足自反性、反对称性和传递性,则称R是X上的一个偏序关系,简称偏序,记为“≤”.同时称集合X和X上的偏序关系R组成的序偶(X,R)为偏序集,记作(X,≤).
定理1设S=(U,A,V,f)是一信息系统,C′为属性集C的任意子集,{ω=k}(1≤k≤n)为该信息系统上的第k层知识空间,若符号“⊆”表示知识空间{{ω=k}∪Grad(C′)}上的包含关系,则序偶({ω=k}∪Grad(C′),⊆)构成一个偏序集.
定理1根据定义7容易证明.
定义8设S=(U,A,V,f)是一信息系统,条件属性子集C′={a1,a2,…,an0},n0≤n,序偶({ω=k}∪Grad(C′),⊆)为一偏序集,任取P∈{ω=k},1≤k≤n0,记
其中P表示由C′中K个属性复合而成的属性,简称复合属性,XP表示由复合属性P产生的信息粒,Xai表示由属性ai产生的信息粒,XP⊆Xai表示由属性P产生的信息粒较由属性ai产生的信息粒细.
由NEk(ai)的取值可判断属性ai在第k层知识空间上是否冗余.
定义9设S=(U,A,V,f)是一信息系统,条件属性C0={a1,a2,…,an},判断在第k层知识空间是否存在NEk(ai)=1,记
则称集合Ck为粒度ω=k下的约简属性集,其中
性质1若存在NE≠0,则在第k层知识空间上有NE个冗余属性.
从性质1可以看出,NE越大,表明粒度ω=k下属性约简能力越强,即NE反映了第k层知识空间上属性的冗余程度,NE也称属性冗余度.
性质2若存在SNE≠0,则在全知识空间上有SNE个冗余属性.
从性质2可以看出,SNE越大,表明在全知识空间上属性约简能力越强.
定义9中的NE和SNE是两个启发式算子,本文利用这两个启发式算子对决策信息系统进行属性约简和规则挖掘.
2 基于偏序关系的粗糙集属性约简及规则提取
2.1基本思想
一般地,在一致决策信息系统中,如果在保持正域不变的前提下进行属性约简,相当于在格P(C),⊂对应的Hasse[12]图中,沿着某条属性链按照自顶向下设计启发式算法,逐渐增加重要属性,直到得到约简结果为止,或是按照自底向上设计启发式算法,逐渐删除不重要属性,直到得到约简结果为止.但上述属性约简方法中,当属性集增大时,约简复杂性会急剧增加.例如,在条件属性集C中含有m个条件属性的决策信息系统中,从∅到C的属性链路有条,从而增加了属性约简的难度.为此,本文给出一种基于偏序关系的粗糙集属性约简方法.该方法通过在不同粒度的知识空间上建立偏序关系,然后,以不同粒层中属性的冗余程度NE和SNE作为启发式算子,对属性逐层进行约简,直到在各粒层上约去所有的冗余属性为止,最后,根据定义3在约简后的属性集上提取最简决策规则.该方法降低了属性约简的复杂性,提高了规则提取的速度,与传统方法形成较好的互补.
2.2属性约简算法描述
给定一个一致决策信息系统S=(U,A,V,f),A=C0∪D,条件属性集C0={a1,a2,…,an},决策属性集D={d},属性约简算法如下:
输入:一致决策信息系统.
输出:约简属性集(约去冗余属性后剩余的属性集).
1)取粒度ω=1,生成知识空间{ω=1}.
2)令k=1.
3)在知识空间{{ω=k}∪Grad(Ck-1)}上建立偏序关系({ω=k}∪Grad(Ck-1),⊆),并计算NE,1≤k≤n.
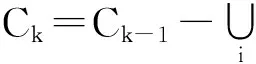
4)取k=k+1,并转入3).
5)输出Ck并计算SNE,算法结束.
2.3基于约简属性集的规则提取
算法描述:
输入:2.2节中约简属性集Ck.
输出:所有最简决策规则集Ruleset.
2)令k=1.
3)取属性P∈Ck,若信息粒U/P⊆U/d,则输出一条规则P→d,并终止所有包含节点P的属性链路上决策规则的搜索,否则转4).
4)取k=k+1,若k≤n-SNE,则转入3),否则转入5).
5)输出所有最简决策规则,算法结束.
3 算法实例
为了考察算法的有效性,选择文献[13]中已知规则的决策信息系统进行对比分析,一致决策信息系统如表1所示,其中,条件属性集C={a,b,c,d},决策属性集D={e}.
根据本文提出的算法对表1进行属性约简及规则挖掘,步骤如下:
步骤1.根据定义6计算决策属性{e}的信息粒:
步骤2.根据2.2节给出的算法,在不同粒层的知识空间上进行属性约简.
取粒度ω=1,则第1层知识空间{ω=1}={{a},{b},{c},{d}},分别计算单个属性下的信息粒{Xa,Xb,Xc,Xd},其中
步骤3.在知识空间{Xa,Xb,Xc,Xd}上建立偏序关系({ω=1},⊆)={Xb,Xc},由偏序集可以看出Xb≤Xc,据此计算在知识空间{ω=1}上NE=1,从而C1={a,b,d},即在第1层知识空间中约去了属性{c}.由于NE≠0且l=3>k+1=2,所以转入步骤4.
步骤4.在属性集C1上取粒度ω=2,得知识空间{Xab,Xbd,Xad},在知识空间{{Xab,Xbd,Xad}∪Grad(Ck-1)}上建立偏序关系并计算得NE=0,表明在第2层知识空间上没有可约的属性,则直接转入步骤5.
步骤5.输出约简属性集C2={a,b,d}.
步骤6.在约简属性集C2上结合2.3节算法进行规则提取.
由例1计算结果及2.3节提供的规则提取算法,可得决策规则为:
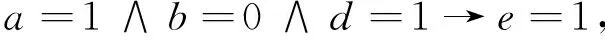
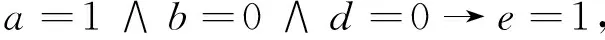
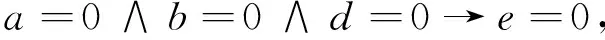
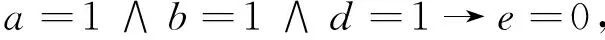
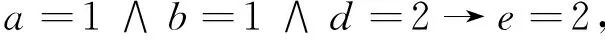
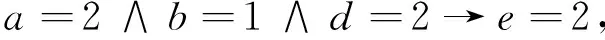
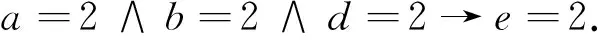
进一步简化,得到简化规则:
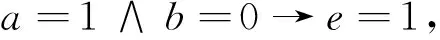

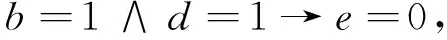

与文献[13]的结果一致.
本例在含有四个条件属性的决策信息系统上,只需建立两次偏序集,经过一次循环计算,即可获得约简属性集,从而降低了属性约简的复杂性,提高了规则提取的速度.
4 结论
本文首先在不同粒度的知识空间上建立偏序关系,并以不同知识空间中属性的冗余程度NE和SNE作为启发式算子,对属性逐步进行约简,直到在各知识空间上约去所有冗余属性为止;然后在约简后的属性集Ck上,沿着格P(Ck),⊂上相应的Hasse图自下而上提取最简决策规则.算法实例表明,该方法降低了属性约简的复杂性,提高了规则提取的速度,并与传统的基于属性约简方法得到的最简决策规则一致.
[1]PAWLAKZ.Roughsets[J].International Journal of Computer and Information Science,1982,11(5):341.
[2]王国英.粗糙集理论与知识发现[M].西安:西安交通大学出版社,2001.
[3]WANG S K,ZIARKO W.On optimal decision rules in decision tables[J].BulletinofPolishAcademyofSciences,1985,33(11):693.
[4]MIAO Duo-qian,WANG Guo-yin,LIU Qing,et al.GranularComputing:Past,Present,andFuture[M].Beijing:Science Press,2007:299.
[5]张向荣,谭山,焦李成.基于商空间粒度计算的SAR 图像分类[J].计算机学报,2007,30(3):483.
[6]苗夺谦,范世栋.知识的粒度计算及其应用[J].系统工程理论与实践,2002,22(1):48.
[7]苗夺谦,徐菲菲,姚一豫,等.粒计算的集合论描述[J].计算机学报,2012,35(2):351.
[8]DAI Jian-hua,PAN Yun-he.Algorithm for acquisition of decisionrules based on classification consistency rate[J].ControlandDecision,2004,19(10):1086.
[9]QIAN Jin,MENG Xiang-ping,LIU Da-you,et al.A mining algorithmfor concise decision rules based on rough sets theory[J].ControlandDecision,2007,22(12):1368.
[10]ZHANG Qing-hua,WANG Guo-yin,LIU Xian-quan.Rule acquisitionalgorithm based on maximal granule[J].PattermRecognitionandArtificialIntelligence,2012,25(3):388.
[11]CHEN Ze-hua,ZHANG Yu,XIE Gang.Mining algorithm for concise decision rules based on granular computing [J].ControlandDecision,2015,30(1):143.
[12]张文修,姚一豫,梁怡.粗糙集与概念格[M].西安:西安交通大学出版社,2006.
[13]CHANG Li-yun,WANG Guo-yin,WU Yu.An approach for attribute reduction and rule generation based on rough set theory[J].JournalofSoftware,1999,10(11):1206.
(责任编辑马宇鸿)
A method to extraction rules based on the partial relation of rough set
CHEN Zhi-en
(Department of Mathematics and Computer Science,Ningxia Normal College,Guyuan 756000,Ningxia,China)
The traditional methods for rule extraction algorithm are attribute reduction and attribute value reduction.But the increasing of attributes number increased the complexity of reduction,and finally affected the speed of rule extraction.In this study,an extraction method based on partial relation of rough set is proposed.Firstly,a partial order relation is constructed in different knowledge spaces;and then,the redundant attributes are reduced according to redundancy which are implied in different knowledge spaces;finally,the decision rule is extracted from the attribute set of the reduction.Examples showed that the method can reduce the complexity of the attribute reduction and improve the speed of rule extraction.
rough set;partial order relation;attribute reduction;rule extraction
10.16783/j.cnki.nwnuz.2016.05.007
2015-08-25;修改稿收到日期:2015-10-28
宁夏自然科学科研基金资助项目(NZ14274,NZ14278,NZ15256);宁夏高校科学研究基金资助项目(ZD20142221);宁夏师范学院科研基金项目
陈志恩(1976—),男,宁夏海原人,副教授,硕士.主要研究方向为粗糙集理论及应用研究.
E-mail:czn2002666@sohu.com
TP 18
A
1001-988Ⅹ(2016)05-0027-05

