基于差分进化算法的散货船“最后分舱装载”计算

， ， ，

(大连海事大学 航海动态仿真和控制交通行业重点实验室， 辽宁 大连 116026)

基于差分进化算法的散货船“最后分舱装载”计算

刘春雷，孙霄峰，吴海波，尹勇

(大连海事大学航海动态仿真和控制交通行业重点实验室，辽宁大连116026)

为实现散货船“最分分舱装载”计算，根据其特点建立“最后分舱装载”的优化模型，将其归结为单目标约束优化问题并采用差分进化算法进行求解。以某25万t散货船为例进行实例计算：实例一为平均吃水变化较大时，利用传统“纵倾力矩法”与上述方法计算得到的平均吃水和吃水差的误差分别为1.026%及8.33%，0%及0%；实例二为平均吃水变化较小时，利用传统“纵倾力矩法”与上述方法计算得到的平均吃水和吃水差的误差分别为0%和2.17%，0%和0%。计算结果表明：上述方法不仅适用于平均吃水变化较小时的“最后分舱装载”计算，而且适用于平均吃水变化较大时的计算，尤其是在平均吃水变化较大时可有效减小误差。

水路运输； 散货船； 配载仪； 最后分舱装载； 差分进化算法

Abstract: An optimization model for bulk carrier “Final Trimming” calculation is built according to the characteristics of the process. The trimming process is regarded as a single-objective optimization with constraints. The differential evolution algorithm is used to solve the problem. Two cases of trimming for a 250 000 tons bulk carrier are carried out for illustration. The first case, associated with large mean draft changes, shows that the deviations of mean draft and trim of draft are 1.026% and 8.33% by traditional “Trimming Moment Method”. The second case, representing the final trimming with only small mean draft change, shows that the deviations of mean draft and trim of draft are 0% and 2.17% by traditional method. On the contrary, the suggested method makes all the deviations zero in both cases, which means that the method can be effective for both general loading and final trimming.

Keywords: waterway transportation; bulk carrier; loading computer; final trimming; differential evolution algorithm

随着航运业不断发展，散货船逐渐趋于大型化，这使得其进出港口时的吃水常受泊位水深的限制。散货船装载货物时通常按预定的配载方案装载，理论上可达到要求的浮态，但实际装载时因装载量和装载位置与理论值不同，导致装货后的浮态与所要求的浮态有较大差别。因此，散货船装货时通常会预留一部分货物用于“最后分舱装载”[1]，使船舶最终的浮态满足进出港要求。

目前针对散货船“最后分舱装载”的计算大多是使用Excel根据“加载100 t吃水法”[2]计算或根据“纵倾力矩法”[3]计算。这2种方法存在每厘米吃水吨数TPC和每厘米纵倾力矩MTC一直不变的假设，当平均吃水和吃水差变化较大时会产生较大的误差。此外，文献[4]采用“内点法”解决质量分配问题，将舱室简化成方体，认为其重心是不依赖于载重量的，而实际上舱室是不规则体，其重心和载重量存在着一一对应的关系，这样的简化也会导致“最后分舱装载”计算产生误差。

针对以上不足，将散货船“最后分舱装载”归结为单目标约束优化问题，建立散货船“最后分舱装载”的优化模型，并将差分进化算法引入到该优化模型的求解中，通过建立离线的舱容表实现散货船的“最后分舱装载”计算，提高计算精度。

1 建立“最后分舱装载”优化模型

“最后分舱装载”结束后，船舶在重力和浮力的作用下能平衡漂浮于静水面，此时可能同时存在横倾和纵倾，但总满足任意浮态下的平衡方程。船舶任意浮态平衡时所确定的平衡方程组[5]为

(1)

1.1 设计变量

1.2 目标函数

通常“最后分舱装载”前船舶的浮态和各个货舱的装载情况是已知的；而“最后分舱装载”结束后船舶处在一个平衡状态，满足船舶任意状态下的平衡方程组(该平衡方程组为一个隐式非线性方程组)。这里主要使用差分进化算法求解该方程组，进而求出“最后分舱装载”的货物分配量，因此平衡方程组中的任何一个方程都可作为目标函数。但是，出于计算简单考虑，根据平衡方程组中的第一式，以用于“最后分舱装载”的货舱总载货量与总排水量变化量差值的绝对值作为目标函数，即

(2)

式(2)中：Mlast为分舱装载后船舶总的排水量;M0为分舱装载前除调整舱之外船舶总的排水量。

1.3约束条件

根据船舶平衡时所确定的浮态方程、每个舱室允许装载的最大装货量和最小装货量，得到以下约束条件。

(3)

式(3)中：pimax为要调整的舱中第i个货舱的最大装货量；xG0，yG0和zG0分别为调整吃水前除调整舱之外船舶重心的纵向坐标、横向坐标及垂向坐标；xGi，yGi和zGi分别为要调整的舱中第i个货舱重心的纵向坐标、横向坐标及垂向坐标；xBlast，yBlast和zBlast分别为调整后所需的船舶浮心的纵向坐标、横向坐标及垂向坐标。

2 用于“最后分舱装载”的差分进化算法

差分进化算法具有结构简单、可调参数少、收敛速度快和鲁棒性强等特点。[6-8]该算法作为一类新兴的优化算法，在处理单目标优化问题方面具有很强的优势，已广泛运用于科学研究和工程实践当中，如控制器参数优化、滤波器设计、数据挖掘和石油化工等。[9]

差分进化算法是从一个随机初始化的种群开始搜索，经过变异、交叉和选择操作产生下一时刻的主种群；该过程重复进行，直到满足停止条件。

2.1 编码及初始化过程

差分进化算法中的个体即优化设计中的设计变量，个体上的每一维变量即为每个设计变量。每个个体的维数与设计变量相同。

1) 设计变量

(4)

2) 种群个体

(5)

式(4)和式(5)中：n为个体的维数；NP为种群规模。

初始种群应尽可能地覆盖整个搜索域，用随机方法产生，每个个体Xi的每一维生成方法为

xi,j=pjmin+rand(0,1)×(pjmax-pjmin)

(6)

式(6)中:rand(0,1)为一个位于0～1的满足均匀分布的随机数；pjmin,pjmax分别为初始化用于“最后分舱装载”的货舱中第j个货舱载重量的最大值和最小值，取pjmin=-0.3pjmax，pjmax=1.3pjmax。

2.2 评价过程

由于约束的存在，在计算每个个体目标函数值的同时还要计算个体的违反约束值[10]，以区分可行个体与不可行个体。

计算每个个体的目标函数值为

(7)

计算每个个体的违反约束值，将约束条件改写成式(8)，其中gr(Xi)及hr(Xi)分别为不等式约束和等式约束；q及m-q分别为不等式约束的数量和等式约束的数量，这里q=2n，m=2n+2。

(8)

个体违反第r个约束的值表示为

(9)

式(9)中:δ为等式约束的容许误差;δ的取值范围为0.001～0.010。由此可得个体的违反约束值为

(10)

当G(Xi)=0时，Xi为可行个体；否则Xi为不可行个体。

2.3 变异过程

对于种群中每个个体Xi，随机生成3个互不相同的整数r1,r2,r3∈{1,2,…,NP}，且要求r1,r2,r3,i互不相同，按照式(11)产生变异个体Vi。

Vi=Xr1+F·(Xr2-Xr3)

(11)

式(11)中：缩放因子F为正数，通常被限定在区间[0,1]内。

2.4 交叉过程

交叉操作按每个个体向量的分量进行。变异产生的变异个体Vi和目标个体Xi按式(12)进行交叉操作产生试验个体Ui。

(12)

式(12)中:sn为随机整数，满足sn∈{1,2,…,n}；对每个解个体需要产生一个sn；Cr为交叉概率因子，Cr∈[0,1]。

2.5 选择过程

差分进化算法釆用的是一对一的贪婪选择。这里使用自适应惩罚函数法[11]对目标个体和试验个体的目标函数值及违反约束程度值进行处理，求得目标个体和试验个体的修正目标函数值分别为F(Xi)及F(Ui)，计算方法为：

3) 计算目标个体和试验个体的距离分别为d(Xi)及d(Ui)。

4) 计算目标个体和试验个体的惩罚项分别为p(Xi)及p(Ui)。

5) 按照式(13)和式(14)计算目标个体及试验个体的修正目标函数值为

则选择过程为

(15)

式(15)中:Xinext为下一代种群中第i个个体。

2.6 终止条件

当问题达到所需精度时即可停止，这样能明显缩短计算时间。同时，进化代数T为另一停止准则，当所设精度不能达到所需时，只要进化代数超过给定的最大进化代数，进化即停止。

3 程序设计

基于Visual Studio 2013开发平台，采用C#语言编写“最后分舱装载”计算程序，其流程图见图1。

4 算例及分析

以某25万吨级矿砂船为例，选择1舱和9舱进行“最后分舱装载”的实例计算。船舶主尺度为：垂线间长LPP=319.5 m;型宽B=57 m;型深D=25 m;设计吃水T=18 m;全船共有9个货舱。

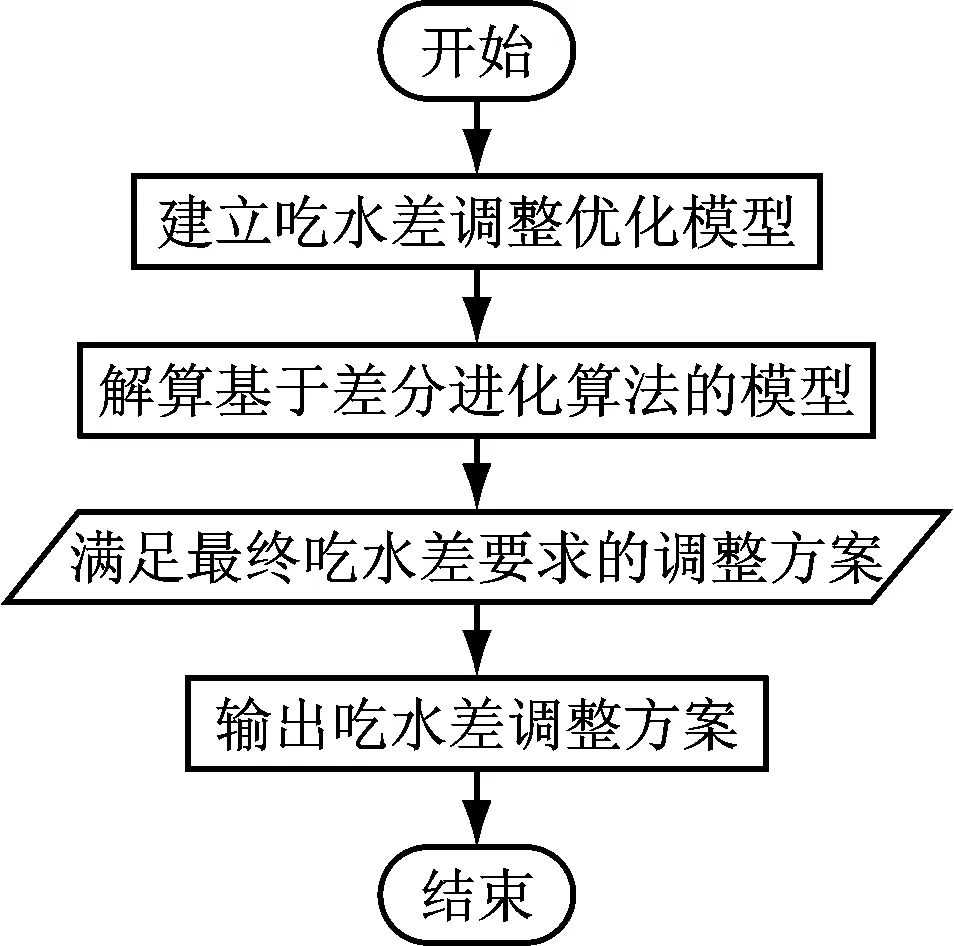
图1 “最后分舱装载”计算流程图

4.1 算例一

货物密度ρRHO=1 t/m3，分舱装载前后平均吃水变化为ΔT=1.1 m。

该船“最后分舱装载”前后的浮态和分舱前各货舱的装载量分别见表1及表2。使用传统的“纵倾力矩法”和文中方法计算1舱及9舱的分货量见表3。将此结果输入到Onboard-Napa装载计算机中得到平均吃水、吃水差和由此计算的误差见表4。

表1 船舶初始浮态和预期最终浮态 m

表2 分舱前各货舱的装载量

表3 传统方法、文中方法的计算结果 t

表4 传统方法与文中方法计算结果对比

利用传统“纵倾力矩法”得到的平均吃水和吃水差分别为3.86 m及-4.07 m，平均吃水和吃水差的误差分别为1.026%及8.33%；使用文中方法得到的平均吃水和吃水差分别为3.90 m及-4.44 m，平均吃水和吃水差的误差均为0%。

4.2 算例二

货物密度ρRHO=1.584 t/m3，分舱装载前后平均吃水变化为ΔT=0.23 m。

该船“最后分舱装载”前后的浮态和分舱前各货舱的装载量分别见表5及表6。使用传统的“纵倾力矩法”和文中方法计算1舱和9舱的分货量见表7。将此结果输入到Onboard-Napa装载计算机中得到平均吃水、吃水差和由此计算的误差见表8。

表5 船舶初始浮态和预期最终浮态 m

表6 分舱前各货舱的装载 t

表7 传统方法、文中方法计算的结果

表8 传统方法与文中方法计算结果对比

利用传统“纵倾力矩法”得到的平均吃水和吃水差分别为18.64 m及-0.45 m，平均吃水和吃水差的误差分别为0%及2.17%；使用文中方法得到的平均吃水和吃水差分别为18.64 m及-0.46 m，平均吃水和吃水差的误差均为0%。

由上述2个算例可知：传统“纵倾力矩法”仅在平均吃水变化小时误差较小，在平均吃水变化较大时误差会变大；文中方法不仅在平均吃水变化小时误差较小，且在平均吃水变化较大时误差也较小。

5 结束语

根据散货船“最后分舱装载”的特点建立散货船“最后分舱装载”的优化模型；基于散货船的舱容表，使用差分进化算法对该模型进行求解。以某25万吨级矿砂船为例进行实例计算，计算结果表明，文中方法不仅适合使用少量货物进行“最后分舱装载”计算，而且适合使用大量货物进行“最后分舱装载”计算，可有效减小误差，使船舶达到预期的平均吃水和吃水差值，具有通用性。该方法已成功应用到自主研发的装载计算中，具有一定的工程实用价值。

这里仅对散货船的艏舱和艉舱进行“最后分舱装载”计算，在以后的工作中将研究使用多舱进行“最后分舱装载”计算。

[1] 东昉. 散装船吃水差调整的一种新方法[J].大连海事大学学报,1996,22(1):15-19.

[2] 栾法敏. 散货船“最后分舱装载”的一种计算方法[J].中国航海,2013,36(2):135-137.

[3] 邢向辉. 散货船装载计算机数学模型及应用的研究[D].大连：大连海事大学，2000.

[4] 雷坤，林焰，纪卓尚. 基于内点法的驳船接载配载方案优化模型[J].中国造船, 2010, 51(2):149-154.

[5] 杜嘉立，姜华. 船舶原理[M].大连：大连海事大学出版社, 2011:13-17.

[6] STOM R, PRICE K. Differential Evolution-A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces[C]. International Computer Science Institute, Berkeley: ICSI, 1995.

[7] STOM R，PRICE K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces [J]. Journal of Global Optimization. 1997, 11(4):341-359.

[8] STOM R, PRICE K, LAMPINEN J A. Differential Evolution: A Practical Approach to Global Optimization[M]. Berlin, Germany: Springer, 2006：1-6.

[9] 徐斌. 基于差分进化算法的多目标优化方法[D]. 上海：华东理工大学,2013：24-32.

[10] 王勇，蔡自兴，周育人,等. 约束优化进化算法[J]. 软件学报, 2009,20(1):11-29.

[11] TESSEMA B, YEN G G. A Self Adaptive Penalty Function Based Algorithm for Constrained Optimization [C]. IEEE Congress on Evolutionary Computation, 2006： 246-253.

Calculation Method of “Final Trimming” for Bulk Carriers Based on Differential Evolution Algorithm

LIUChunlei，SUNXiaofeng，WUHaibo，YINYong

(Key Laboratory of Marine Dynamic Simulation & Control for Ministry of Transport，Dalian Maritime University, Dalian 116026, China)

1000-4653(2016)04-0052-04

U693.6

A

2016-07-12

国家高技术研究发展计划(“八六三”计划)课题(2015AA016404)

刘春雷(1987—)，男，河北保定人，博士生，研究方向为散货船智能化配载。E-mail：18940930042@qq.com 孙霄峰(1978—)，男，山东济宁人，副教授，博士生，研究方向为船舶操纵性及航海动态仿真。E-mail：xfsun_dlmu@163.com