具有非线性捕获项的多时滞HollingIII型功能反应捕食模型的正周期解

刘小刚，任睿超，孙　洁

（西北大学 现代学院，陕西 西安 710130）

具有非线性捕获项的多时滞HollingIII型功能反应捕食模型的正周期解

刘小刚，任睿超，孙洁

（西北大学 现代学院，陕西 西安 710130）

利用重合度理论中的延拓定理讨论了一类具有非线性捕获项的多时滞HollingIII型功能反应捕食模型的正周期解的存在性，得到了模型正周期解存在的充分条件，推广了已有的某些结果。

多时滞；正周期解；HollingIII功能反应；重合度

1　引言

生物种群的持续生存是数学生态学中捕食理论及其有关课题的一个重要方面。近年来，基于三种功能反应的多时滞多物种生态系统周期解受到了学术界的重视，具有收获率的系统由于存在开发项，往往表现出更复杂的动力学行为，很多学者在这方面做出了贡献[1-3]，例如，王晖[4]运用重合度的方法研究了以下一类基于比率的且具有收获率和时滞的捕食系统：

的周期解的存在性，其中x1(t),x2(t)分别表示t时刻食饵种群与捕食者种群的密度；ai(t),bi(t),αi(t),hi(t) (i=1,2),m(t)是连续的有界严格正周期函数，hi(t) (i=1,2)表示两个种群的收获率，但是此系统没有考虑到多滞量的影响。

谢小丽[5]等研究了具有非线性捕获项的多时滞Hassel-Varley型功能反应食饵捕食者系统：

并满足初始条件：

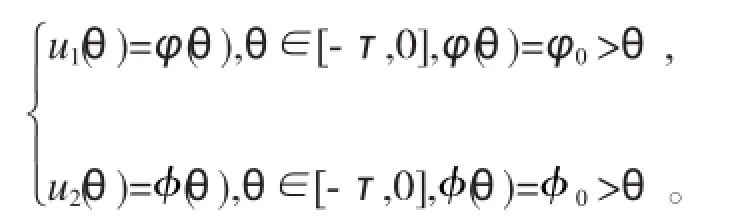
的正周期解的存在性。其中u1(t),u2(t)分别表示t时刻食饵种群与捕食者种群的密度；r1(t)为食饵的内禀增长率，b(t)为食饵的内部制约率，r2(t)为捕食者的死亡率，a1(t),a2(t)分别表示食饵与捕食者的转化率，γ为Hassell-Varley系数，m(t)为半饱和量，但系统的滞量要求必须满足一定的条件（如滞量的导数要小于1等）。

陈凤德[6]等研究了多滞量捕食模型：

的正周期解的存在性，其中N1(t),N2(t)分别表示t时刻食饵种群与捕食者种群的密度，r1,r2,ai,bj,ci, dj,τi,σj,βj,αi∶R→[0,+∞]都是连续的ω周期函数，此系统存在同样的问题。

本文在这些研究的基础上，进一步讨论任意有限个滞量且带有非线性捕获项与HollingIII型功能反应捕食模型：

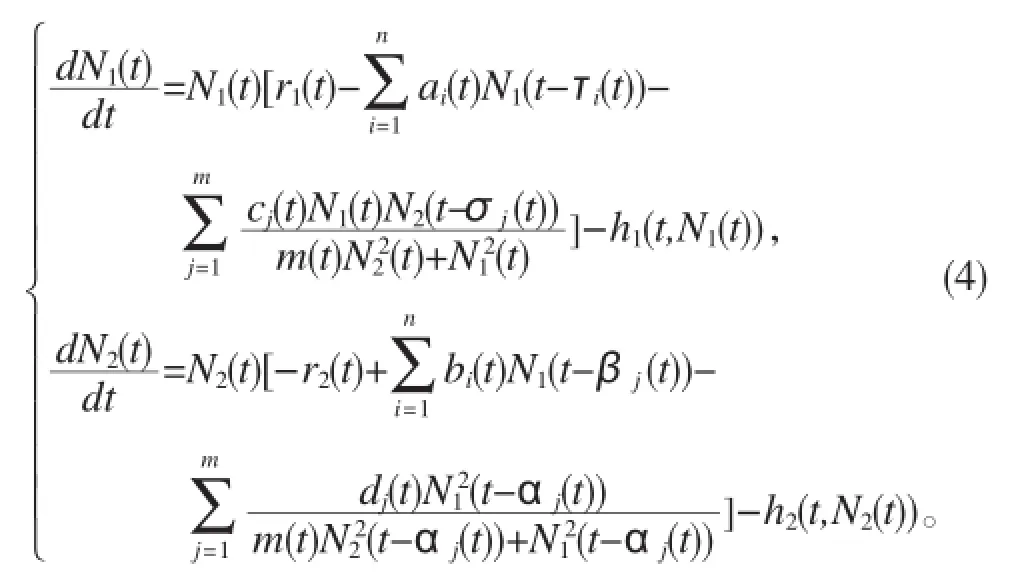
的正周期解的存在性。其中N1(t)，N2(t)分别表示t时刻食饵种群与捕食者种群的密度；r1(t)是食饵种群的内禀增长率；r2(t)为捕食者的死亡率；ai(t)(i=1,2)为食饵的内部制约率；cj(t),dj(t)(j=1,2)分别是食饵和捕食者的转化率；hi(t,Ni(t))(i=1,2)表示两个种群的收获率；m(t),r2(t),ai(t),bi(t),cj(t),dj(t)(i,j=1,2)都是在R上连续的ω正周期函数；r1(t),τi(t),σj(t), βi(t),αj(t)(i,j=1,2)都是在R上连续的ω周期函数，此外，假设

2　预备知识和引理

为了证明周期解的存在性，笔者引入重合度理论中的延拓定理[6]，根据文献[6]中的重合度理论，设X,Z是两个Banach空间，L：DomLX→Z为线性映射，N：X→Z为连续映射，如果dim kerL= Codim ImL是Z中的闭子集，则称映射L为指标为零的Fredholm映射。如果L是指标为零的Fredholm映射且存在连续投影P：X→ X以及Q：Z→Z，使得ImP=KerL,ImL=KerQ=Im(I-Q)，则L| DomLKerP：(I-P)X→ImL可逆，设起逆映射为Kp，设Q为X中的有界开集，如果QN()有界且Kp(I-Q)N：→X是紧的，则称N在上是L紧的。由于ImQ与KerL同构，因而存在同构映射J：ImQ→KerL。

引理1[6]（延拓定理） 设X,Z是两个Banach空间，L为指标为零的Fredholm算子，假设N：→Z在是L紧的，这里Q是X上的一个有界开集，进一步，如果

为了后文叙述方便，笔者引入记号：

3　周期解的存在性

定理1设模型（4）的系数函数满足下列条件：

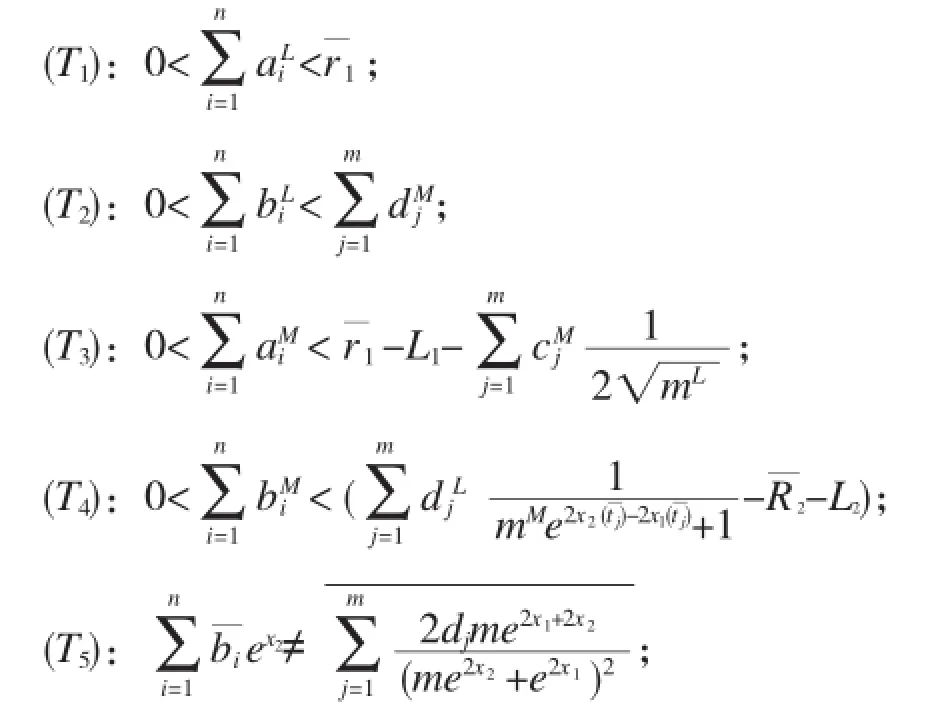
则模型（4）至少存在一个ω周期正解。

证明：作变换Ni(t)=exi(t)，i=1,2，则模型（4）化为：

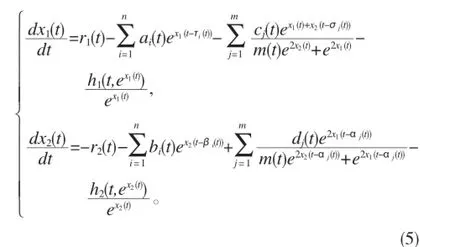
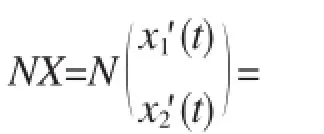
如果模型（5）存在周期解x(t)，则满足

下面只需证明方程（6）有解即可。定义映射P∶X→X，Q∶Z→Z，使得

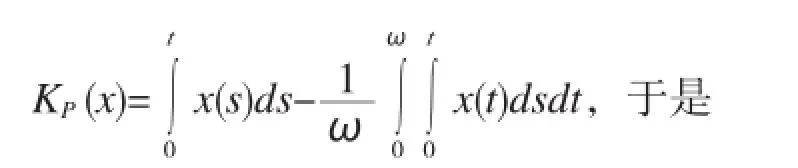
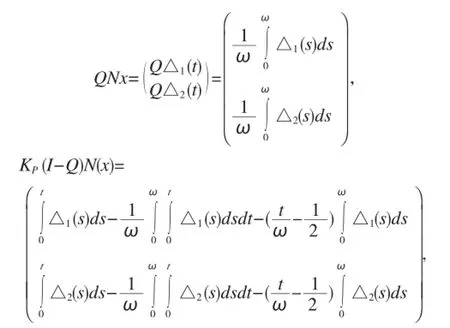
显然 QN和 KP(I-Q)N是连续的，利用Arezela-Asoli定理，易证明KP(I-Q)N对任意的有界集ΩX是紧致集，而且QN是紧的。因此，对任意的有界集ΩX，N在是L紧的。

考虑算子方程

对（7）式两边从0到ω积分，有

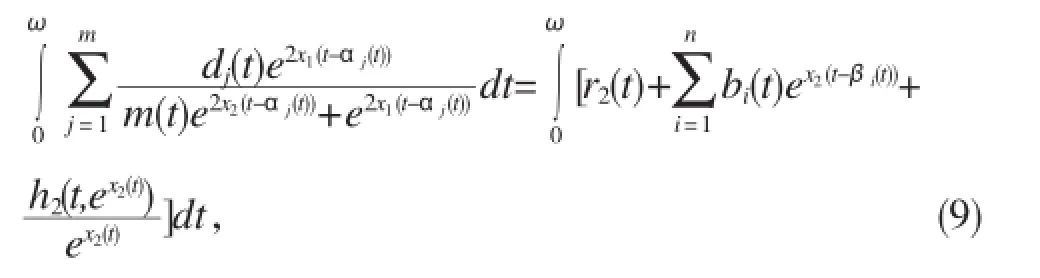
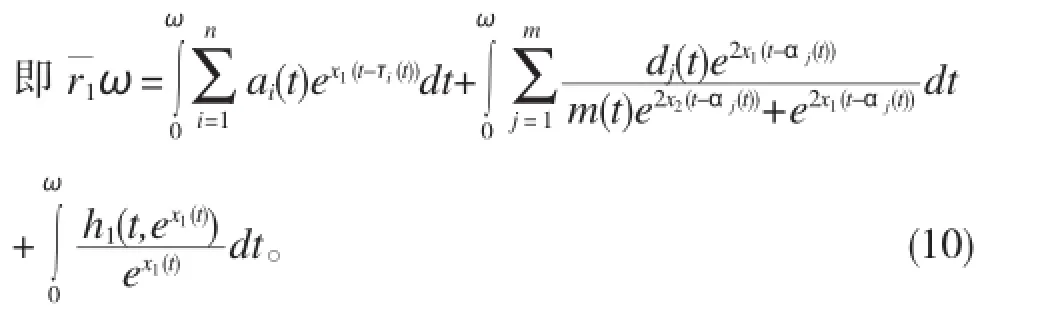
根据（7）式及（10）式，有

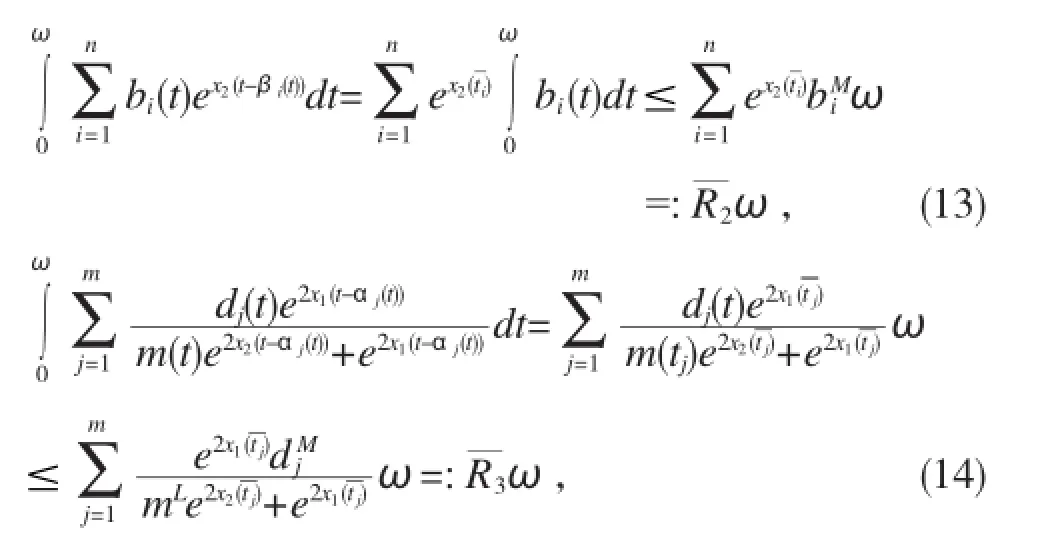
同理，根据(7)、(13)、(14)式，有

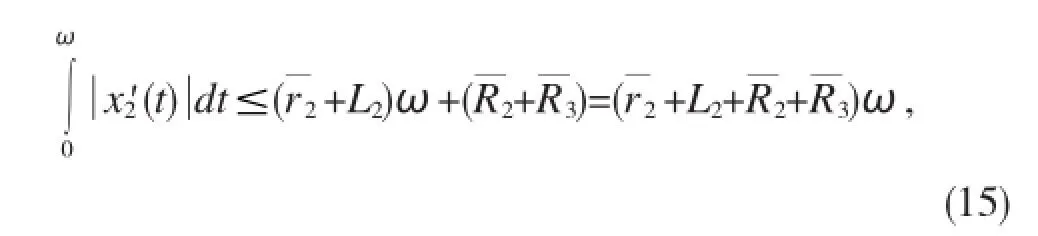
根据(8)式，有

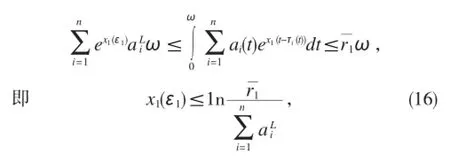
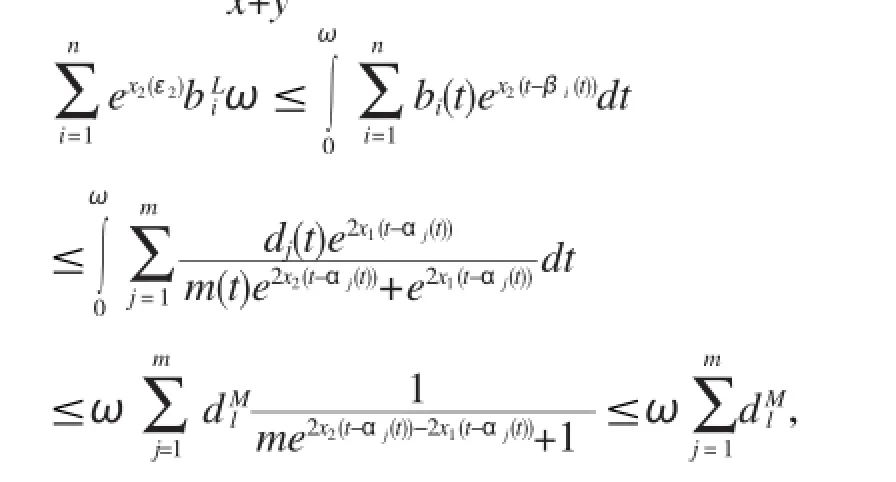
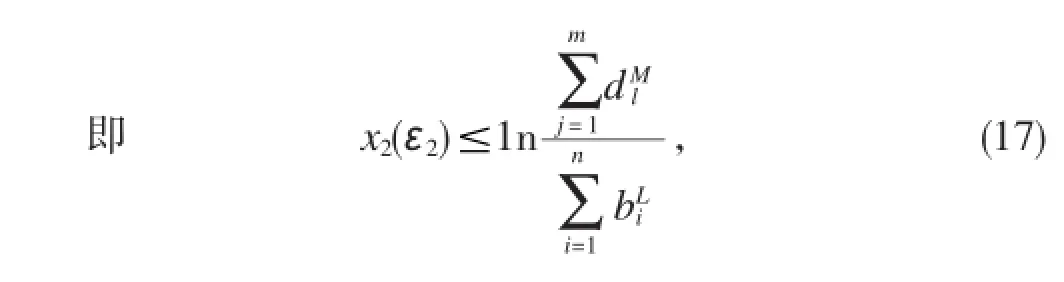
根据(12)～(17)式，有

由（8）式以及（20）式，有

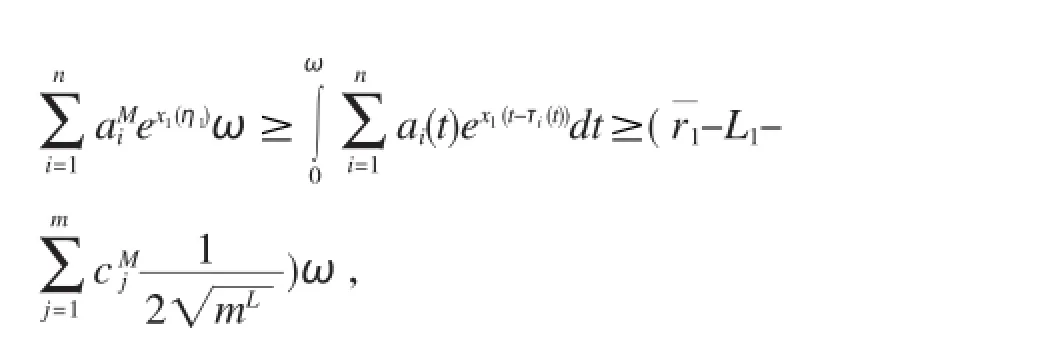
根据(9)式以及(14)式，有

根据(12)式以及(21)式，有

同理根据(15)式以及(22)式，有

由(18)式和(23)式，得

由(19)式和(24)式，得

其中H5和H6与λ无关。

定义H=H5+H6+H7，其中H7充分大，使得对于代数方程：

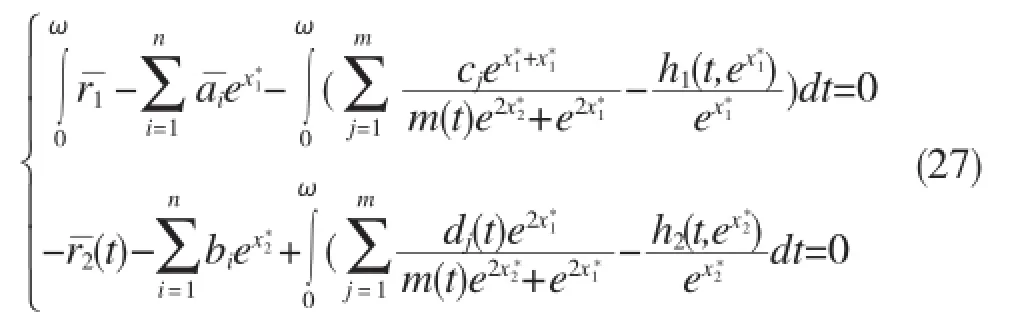
定义映射J：lmQ→KerL，则

的唯一解，且满足

所以，模型（4）至少存在一个以ω为周期的正周期解。

[1]WANG Kai.Periodic solutions to a delayed predator-prey model with Hassell-Varley type functional response[J]. Nonlinear Analysis：Real Word Application，2011，12 （1）：137-145.

[2]ZHANG Guodong，SHEN Boshan.Positive periodic solutions in anonselective harvesting predator-prey model with multiple delays[J].Jpurnal of MathematicalAnalysis and Application，2012，395（1）：298-306.

[3]ZHAO Xiaohua，YI Qizhi.Permanence and Periodic Solution for nonautonomous Competion-Predator System with Type II Function Response[J].Ann of Diff Eqs，2003，19（3）：464-473.

[4]王晖.一类基于比率的且具有收获率和时滞的捕食系统的周期解[J].纯粹数学与应用数学，2013，29（5）：521-528.

[5]谢小丽，陈晓星，游华.具有非线性捕获项的多时滞Hassell-Varley型功能性反应食饵-捕食者系统的周期解[J].福州大学学报（自然科学版），2014，42（3）：353-359.

[6]陈凤德，史金麟，陈晓星.多滞量捕食模型的正周期解[J].生物数学学报，2005，20（1）：51-57.

[7]吴亭.基于比率依赖Beddington-DeAngelis功能反应的离散n-种群竞争捕食系统的持久性[J].纯粹数学与应用数学，2010，27（4）：437-441.

[8]张正球.几类泛函微分方程周期解得存在性[D].长沙：湖南大学，2001.

[9]EDOARDO BERETTA.Global analyses in some delayed ratio-dependentpredatorSystems[J].Nonlinearanalysis Theory Math Applic，1997，32（3）：381-408.

【责任编校李林霞】

Periodic Solutions to Multiple Delayed HollingIII Type Functional Response System with Nonlinear Harvesting

LIU Xiaogang，REN Ruichao，SUNJie
（Modern College of Northwest University，Xi’an 710130，Shaanxi，China）

By using the method of coincidence degree theory，we study the existence of positive Periodic solutions to multiple delayed HollingIII type functional response systemwith nonlinear harvesting.And sufficient conditions and some results in the paper are proved.

several delays；positive periodic solutions；HollingIII type functional response system；coincidence degree

O175.13

A

1674-0092（2016）02-0101-05

10.16858/j.issn.1674-0092.2016.02.024

2015-10-09

陕西省教育厅专项科研计划项目（14JK2146）

刘小刚，男，陕西延安人，西北大学现代学院讲师，硕士，主要从事微分方程与动力系统研究。