跨区互联电网热稳定安全域边界近似方法

姜 涛贾宏杰姜懿郎孔祥玉陆 宁

（1. 智能电网教育部重点实验室（天津大学） 天津 300072 2. 北卡罗来纳州立大学电气与计算机工程系 罗利 27695-791）

跨区互联电网热稳定安全域边界近似方法

姜 涛1贾宏杰1姜懿郎1孔祥玉1陆 宁2

（1. 智能电网教育部重点实验室（天津大学） 天津 300072 2. 北卡罗来纳州立大学电气与计算机工程系 罗利 27695-791）

基于多元非线性回归理论，探究满足跨区域互联大电网联络断面支路N−1热稳定约束下的热稳定安全域边界（SRB）近似算法。构建多种电力系统热稳定安全域边界近似模型，引入模型拟合优度、总体显著性水平、变量显著性水平以及参数置信区间等概念，对所建模型进行全面、综合的评估，判定所提模型的可靠程度，确定合理的安全域边界近似模型。与实际区域互联大电网相结合，通过大量计算结果对所提模型验证、评估，确定可综合、全面反映安全域边界特性的近似模型；在此基础上提出并验证电力系统热稳定安全域边界近似的快速算法及多支路热稳约束下的电力系统热稳定安全域边界近似算法。最后将所提方法应用到实际电网中，构建满足实际跨区域互联大电网联络断面支路N−1约束的热稳定安全域。

电力系统 N−1 热稳定 安全域 非线性回归模型

0 引言

随着电力工业快速发展、受端系统规模不断扩大，特别是用电负荷迅猛增长、最高用电负荷占比逐步增加，而受端系统电源建设不足，大量电能需远距离输送，迫使受端系统对区域外电力依赖度不断增加，区域间断面输电功率日益接近其传输极限，威胁着电网的安全稳定运行[1-4]。此外，受环境、建设成本等因素制约，区域间输电走廊建设面临多重不确定性风险，区域间断面常运行在重载工况下，这些因素导致世界范围内因关键断面支路过载引发的电网联锁事故频频发生，造成了巨大的经济损失和严重的社会影响。区域间联络断面的安全稳定问题越来越被研究和运行人员重视[5-9]，而 N−1下断面支路的热稳定性作为断面安全稳定校验的基本要求，尤其被区域调度控制中心的运行和调度人员关注[10,11]。

目前，N−1下断面支路的热稳定校验完全基于“极限计算”模式，极限计算模式简单易用，已在电网的运行和规划中发挥了巨大的作用。但随着电网的发展，极限模式也暴露出越来越多的局限性，集中体现在两个方面：①在极限之下也可能是不安全的；②极限本身随不同的运行方式变化较大而某一个固定的极限值难以确保电网的安全。随着电网规模的扩大和新能源的大规模接入，影响断面潮流的因素越来越多，呈现出明显的多维特性，仅仅采用过去简单的、一维的极限方法控制电网的运行已经不能满足大电网安全运行和精细化管理的要求，亟需发展新的技术手段来解决该问题，而多维空间安全域方法就是一种最理想、最实用的新技术解决方案[11]。

安全域是定义在参数空间上，满足各类安全稳定性约束的运行点集。安全域计算得到的是参数空间中系统能够安全运行的一片连续区域，得到安全域后，断面的N−1热稳定校验变得简单——只需评估运行方式（运行点）在参数空间中的位置是否位于安全域之内，就可判断其是否安全。进一步还可以测量运行点到不同方向的安全域边界的距离来定量评估当前运行方式下断面的安全性以及方式安排的鲁棒性，并给出相应预防控制措施调整系统断面潮流分布，改善断面支路N−1后的安全稳定性[12]。基于多维空间安全域的断面监测与控制已在国家电力调度中心、河南电力调度中心和天津电力调度中心得到了实际应用[12]。文献[13]指出，利用超平面的思想将北美传统的二维安全域Nomogram拓展到多维空间，能考虑多种输电通道、发电以及负荷的影响，并且可以通过多维空间确认系统的薄弱环节、发现最优的控制方向，是北美电力控制中心未来主要发展的领域之一。同时，随着广域量测系统（Wide-Area Measurement Systems, WAMS）在电力系统中的大规模应用，为电力系统在广域范围内实现断面热稳定在线监测提供了新技术[13-15]。借助广域量测信息在线监测系统的关键支路的热稳定性已成为电力系统热稳定安全域研究的重要方向。文献[14]利用由WAMS实时提供的系统状态变量（节点电压幅值和相角）计算仿射变换矩阵，将支路功率映射到节点注入功率空间，在注入参数空间构建输电线路热稳定；文献[15]进一步提出利用广域量测信息构建电力系统广域安全域的基本概念、模型及算法，探讨了基于广域量测信息构建的广域安全域在电力系统中的应用前景。上述方法在构建电力系统的安全域时都基于一个假设，即电力系统的安全域边界可以用超平面近似。而采用超平面近似时，为避免安全域内部出现空洞，必然会将一定的系统安全运行点排除在安全域外而造成安全域的保守性。为降低安全域的保守性，通常做法是对安全域边界采用超平面分段近似。采用超平面线性近似虽能获得较为理想的安全域，但也加重了计算量。因此，如何在兼顾安全域计算准确度和计算工作量的基础上，开发合理的安全域边界近似算法尤为重要。

本文以多元非线性回归模型为基础，以跨区域互联电网调度中心所关注的断面热稳定为研究重点，构建基于多元非线性回归模型的跨区互联电网断面热稳定安全域，通过多元非线性回归的相关理论研究电力系统热稳定安全域边界的近似方法，并将所提方法应用到实际电网中，通过实例研究，确定合理的电力系统热稳定安全域边界近似算法，最后在参数空间中，构建了N−1下满足实际电网送、受电断面支路热稳定约束的热稳定安全域。

1 计及N−1的断面热稳定安全域

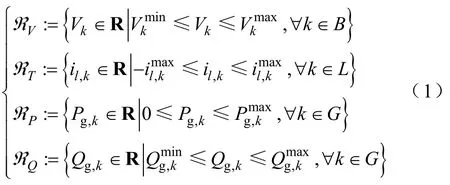
电力系统的静态安全约束是由节点电压幅值约束Vℜ、支路热稳定约束Tℜ、有功发电约束Pℜ和无功发电约束Qℜ 共同组成，其数学表达式为式中，B、L和 G分别为系统中节点、支路及发电机的集合；Vk、il,k、Pg,k和 Qg,k分别为节点的电压幅值、支路流过的电流、发电机的有功出力和无功出力；上标max、min分别为参数值的上、下限。

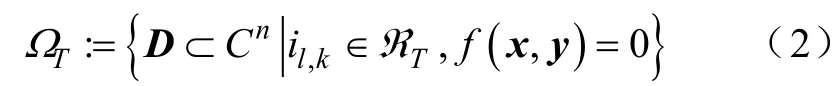
式中，f(x,y)为系统潮流方程；x为状态变量向量；y为节点的注入复功率向量；D为系统的描述性参数向量，其元素可以为支路电流、功率、支路相位差、区域发电机总出力、区域总负荷和断面有功功率等。

实际运行中，调度运行人员不仅关心当前状态下系统的热稳定问题，更关心系统在当前状态下N−1后的系统热稳定性，进一步由式（2）得到描述性参数空间中，N−1下的电力系统热稳定域数学表达式为

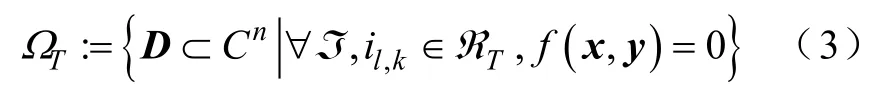
式中，ℑ为系统N−1时的任意故障。

进一步由式（3）得到参数空间中，电力系统热稳定域边界上界点的支路电流必满足支路约束方程

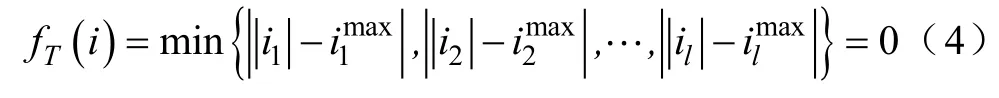
式中，fT(i)表示 N−1时，系统中至少有一条支路热稳定处于临界状态；l为系统的支路数量。对于实际电网而言，其支路数成百上千，即 l取值远大于3，若以各条支路有功功率为研究对象，作为描述性参数向量D中元素选取为坐标轴，所构建的电力系统热稳定安全域必定是高维度。如何将此高维度安全域从概念推向实用化，面临两大主要难题：①如何可视化，从人类视角出发，综合安全域在二维空间和三维空间可观性强；②如何求解边界，高维空间中安全域边界拓扑性质复杂且难以计算，制约着高维空间安全域的应用。

目前在实际电网中构建电力系统综合安全域的总体思路为：在尽量保留系统关键性信息的前提下，结合实际系统所面临的主要问题，将高维空间的综合安全域化简到二维或三维空间中，利用已实际应用、成熟的二维或三维空间的安全域技术构建实际电网的安全域。为此，本文从全局角度出发，以区域电网调度控制中心运行和研究人员最为关心的系统送、受断面为主要研究对象，选择其有功功率及影响上述断面的关键性电厂和区域的有功出力作为描述性参数构建满足断面支路N−1约束的热稳定安全域，其中送、受电断面由区域电网电力调度控制中心定义，关键性电厂和区域结合电网运行经验和功率传输转移分布因子（Power Transfer Distribution Factor，PTDF）共同确定。

2 安全域边界的常用近似方法

在电力系统多维参数空间中，尽管通过各种搜索算法，可以追踪到满足系统N−1热稳定约束的边界和临界点，这些散布在空间中的一系列临界点构成了电力系统N−1下的热稳定域边界。但这种边界没有一个可明确描述其特性的数学解析表达式，在实际电力系统中不具有工程应用价值。为此相关学者开展了大量的研究工作，研究安全域的边界拓扑性质，确定采用何种方法对安全域边界进行近似，以期得到安全域边界的解析表达式，实现安全域的工程实用化。文献[12]在安全域的研究中发现“在工程关心的范围内，安全域边界可用一个或几个超平面来近似描述”。 基于超平面近似的电力安全域如图1所示，图中超平面约束下的安全域可以转换为一系列线性不等式

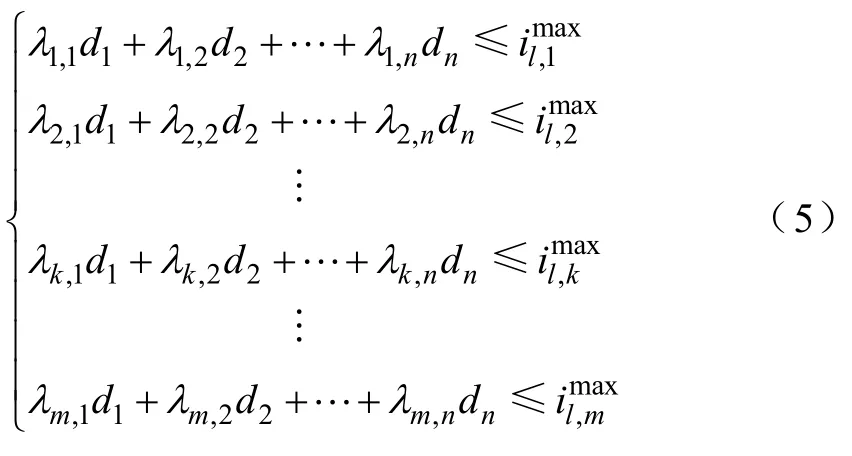
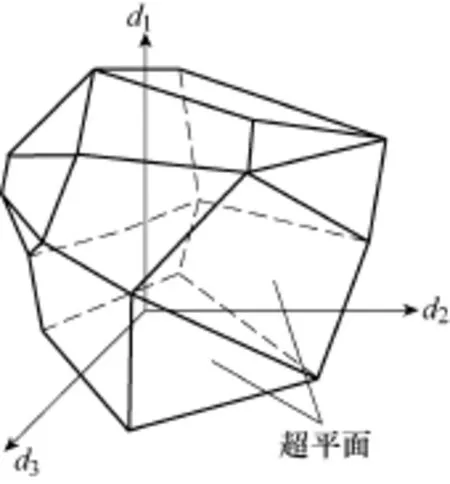
图1　基于超平面近似的安全域示意图Fig.1 Conceptual view of approximated security region

式中，k表示拟合该安全域边界的第 k个超平面，对应于式中的第k个不等式，表示系统在运行时需满足第 k个支路的热稳定约束；n为该安全域的空间维数为第k超平面的系数。若在某一运行点满足式（5），则系统运行在安全域内，不会发生N−1支路过载现象；反之，则系统运行在安全域外，N−1后系统将出现支路过载。利用超平面对安全域近似，便于开发出计算安全域的快速算法，实现安全域的可视化，大大降低电力系统参数不确定性时电力系统概率安全性评估的计算量，使一大类电力系统最优化问题中稳定约束处理难的问题变得十分简易。而采用超平面近似的关键是求解式（5）中超平面系数λk，由式（4）和式（5）可知，位于安全域的第k个超平面Hk上的运行点满足

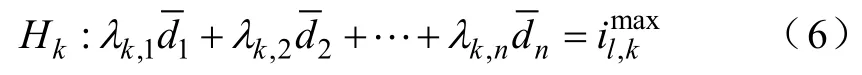
目前常采用最小二乘求解式（6）第k个超平面Hk的系数λk。满足式（6）最小二乘误差平方和最小的方程为

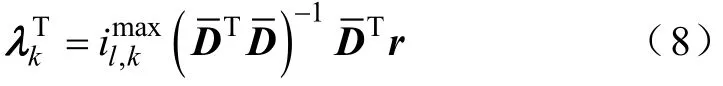
通过式（8）可求出第k个超平面的系数。同理，采用上述方法，依次可求出组成安全域的m个超平面的系数。

为整体评估超平面拟合的准确度，进一步定义了超平面近似安全域边界的总体相对误差为

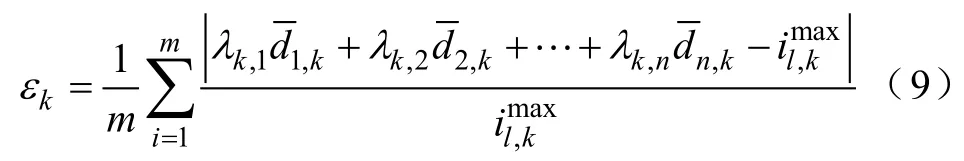
式中，k表示第 k个超平面；m为安全域边界上的临界点个数。

由式（9）求得kε，便可评估采用超平面拟合安全域边界的效果。若所得相对误差kε过大，则可以考虑采用多个超平面进行拟合，直到满足所需准确度为止。采用上述超平面方法所构建的电力系统动态稳定域和电压稳定域的准确性和有效性已在文献[16-20]中得到验证，并在实际工程中得到了应用。而对于“目前运行人员重点关注的区域间断面热稳定安全域是否可以采用这种方法构建，所构建的安全域准确度是否满足要求，其保守性如何?”目前尚无研究人员对此进行深入研究，此外采用kε评价安全域边界的拟合准确度仍具有一定的片面性，并不能综合、全面地反映评估超平面拟合安全域边界的效果。为此本文在已有研究基础上，基于多元非线性回归模型构建热稳定安全域边界近似模型，综合、全面地探究整个热稳定安全域边界的近似特性。

3 基于多元非线性回归模型的电力系统安全域边界近似

在图1所示的描述性参数空间中，针对某一支路热稳定约束下的安全域边界，构建近似安全域边界的非线性多元回归模型为

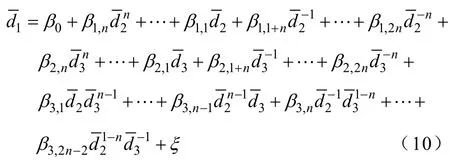
式中，上标“−”表示变量在临界点处的值；d1为因变量，表示断面传输的有功功率；d2、d3为自变量，表示影响断面联络线N−1热稳定的关键性发电厂或区域的有功出力；β0, β1,n,⋅⋅, β1,1, β1,1+n,⋅⋅, β1,2n与β2,n,⋅⋅, β2,1, β2,1+n,⋅⋅, β2,2n均为回归系数；ξ为误差。在实际运行中，考虑到关键性发电厂或区域的有功出力为0时断面传输功率不会发生剧烈跳变，可知式中β1,1+n,⋅⋅, β1,2n与β2,1+n,⋅⋅, β2,2n均为 0，则上式可化简为

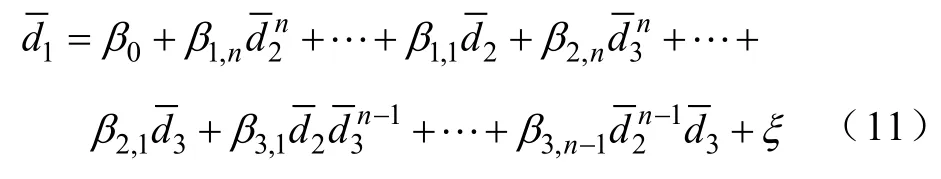
式（11）即为基于非线性回归模型所构建的电力系统热稳定安全域边界近似表达式。将上述自变量的高次方均记为新变量的一次方，则可借助已成熟的线性回归模型方法来求解式（11）模型的回归系数和回归误差，进一步采用拟合优度检验、模型总体显著性检验、变量显著性检验以及参数置信区间估计对所构建安全域边界近似模型进行检验，以判定所提模型拟合电力系统热稳定安全域边界的可靠程度。

3.1拟合优度检验

在多元线性回归模型中，拟合优度检验常用来衡量样本回归线对样本观测值的拟合程度，本文通过拟合优度检验来评估所提模型对安全域边界上临界点的拟合准确度。在拟合优度检验中首先引入总离差平方和 TSS、回归平方和 ESS及残差平方和RSS，其中

即TSS可分解为RSS和ESS两部分。ESS反映了TSS中可由样本回归线解释的部分，ESS越大，RSS就越小，表明模型对安全域边界的拟合程度越高。因此，可用ESS在TSS中的比重（即可决系数R2）来衡量安全域边界的拟合程度

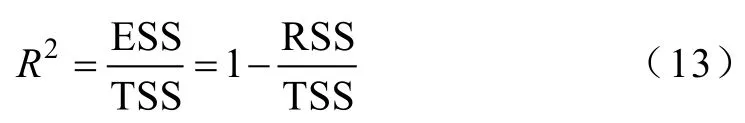
式中，R2越接近1表明安全域边界的拟合准确度越高。实际应用时，由于RSS随描述自变量个数的增加而减少，但R2的增大与拟合好坏无关，因此本文进一步引入调整的可决系数来评估模型对安全域边界临界点的拟合准确度。

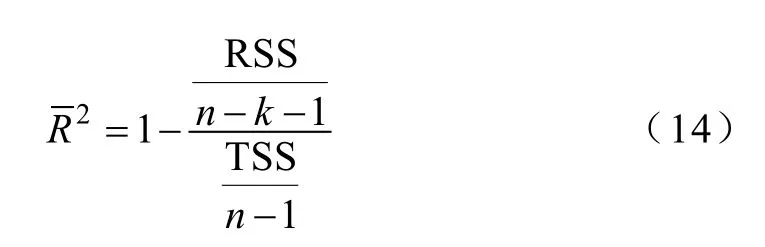
式中，n−k−1为RSS的自由度；n−1为TSS的自由度。

3.2模型总体显著性检验

拟合优度检验从已估计模型出发检验模型对安全域边界上临界点的拟合程度，但不能给出一个严格的结论。为此，本文进一步引入F检验，从安全域边界上临界点出发，校验所估计模型的总体显著性。根据假设检验原理，在假设所提模型线性无关的条件下，统计量服从区间分布为（k,n−k−1）自由度的F分布

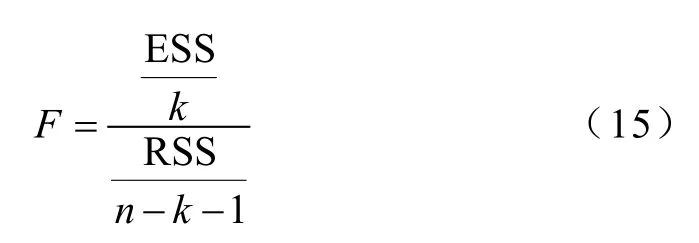
在给定显著性水平α ，当F＞Fα时，则拒绝原假设，即原模型总体线性关系显著；当F≤Fα时，接受原假设，即原模型总体线性关系不显著。

3.3变量的显著性检验

在构建安全域边界近似模型过程中，模型的总体显著性并不能说明每个变量对自变量的影响都是显著的，因此必须对近似模型中的每个变量进行显著性检验，以决定是否作为自变量而保留在模型中。若某一变量对自变量的影响不显著，则剔除该变量，以建立更为简单的安全域边界近似模型。为检验模型中变量的显著性，本文采用 t检验对模型中变量进行显著性检验，t值越大则该变量越显著，需保留；反之则可忽略，将其剔除。

3.4参数的置信区间

通过拟合优度检验、模型总体线性的显著性检验及变量的显著性检验可对安全域边界近似模型的合理性和有效性进行验证。但对于所估计的参数离其实际值的远近，还需进一步估计参数的置信区间。置信区间宽度越窄，模型回归系数的准确度越高，反之则越低。通过对置信区间的估计可评估出模型回归系数的准确度，进而得到满足准确度的电力系统热稳定安全域边界近似模型。

4 算例分析

为探究和验证本文所提出的电力系统热稳定安全域边界近似方法可行性和有效性，本文以CSG为例进行研究和分析。研究过程中CSG的断面热稳定域临界点均采用基于文献[21, 22]所开发的 CSG N−1断面极限计算软件进行搜索。目前CSG已形成覆盖YN、GZ、GX、GD和HN五个省份的交、直流互联区域性大电网，网内已分别形成了YN交流送出断面、GZ交流送出断面和GD交流受入断面三个典型的送、受电断面。系统正常运行时，CSG电力调度控制中心主要关心断面N−1后，断面支路过载所诱发的联锁故障[21]，为此本文拟构建计及CSG关键送、受电断面N−1约束的热稳定安全域。限于文章篇幅，重点对GD受入断面的热稳定安全域构建进行说明。

GD入口断面主要有GS双线、WL双线、HL双线及YM/MD双线构成。长期运行经验表明：GD入口断面北通道的GS双线及南通道的YM/MD双线在断面联络线N−1后都会出现热稳越限的风险，而中通道的WL双线和HL双线基本不存在热稳越限的风险（大量仿真结果表明GS和YM/MD双线总先于WL和HL双线出现热稳越限），因此GD入口断面的热稳主要受GS和YM/MD双线的热稳越限约束。研究表明影响GS及YM/MD热稳约束的关键性电厂和区域主要有GPT、YX、TS电厂及QBF地区的有功出力[21,23]。为此在所构建的三维空间热稳定安全域中d1为GD断面传输的有功功率，d2、d3分别为GPT、YX、TS或QBF的有功出力，约束条件为N−1下的GS及YM/MD热稳约束。

4.1单一热稳定约束下GD断面热稳定安全域构建

首先以YM双线热稳约束为例，以YX有功出力为d2、TS有功出力为d3，采用所开发的CSG N−1断面极限计算软件在 YX和 TS可出力范围内搜索断面热稳定域的临界点, 构成临界点集合sYM。根据集合sYM，首先构造热稳定域边界近似线性模型

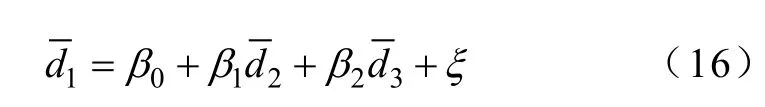
借助线性回归的方法对所构建安全域边界近似模型进行综合评估，式（16）中各变量的回归系数分别为β0=9 343.750 0、β1=0.322 4和β2=0.913 5，模型预测值与实际值分布及模型预测残差分别如图2和图3所示，对应的临界点拟合优度参数R2=0.997 3和模型总体显著性检验的F值为10 611.4；常数项（以下记为 Intercept）、d2和 d3显著性检验的t分布分别为2 922.25、67.61和131.05；β0、β1和β2满足95%置信度下的置信区间分别为β0= [9 337.349 6, 9 350.150 4]、β1=[0.312 8, 0.331 9]和β2=[0.899 6, 0.927 5]。

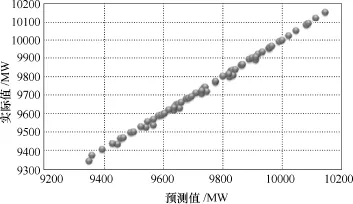
图2　线性模型下d1预测值与实际值在空间中分布Fig.2 Distribution of predicted values vs actual values for d1via linear regression model

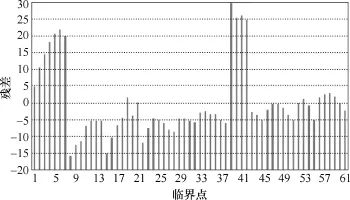
图3　线性模型下d1的残差Fig.3 Residual of d1via linear regression model

上述拟合优度、模型显著性校验、变量显著性校验和参数置信区间的计算结果及图2、图3表明，采用线性回归模型逼近YM热稳定约束下的热稳定安全域边界，具有极高的准确度，模型可准确预测系统的热稳定临界点。进一步构建热稳定域边界近似的二次模型

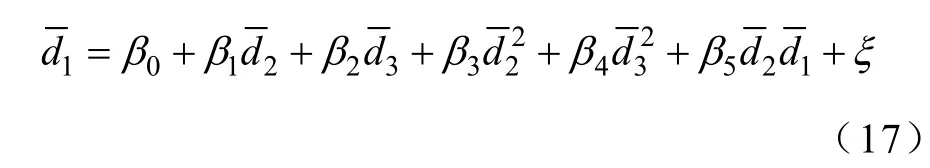
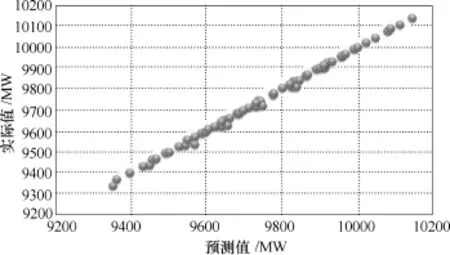
图4　二次模型下d1预测值与实际值在空间中分布Fig.4 Distribution of predicted values vs actual values for d1via quadratic regression model

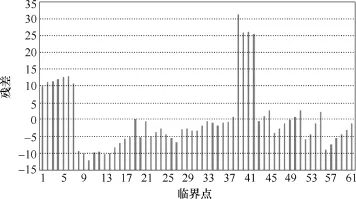
图5　二次模型下d1的残差Fig.5 Residual of d1via quadratic regression model

类似式（16）的计算方法，式（17）中各变量的回归系数分别为β0=9 338.695 1、β1=0.305 57、β2=0.963 7、β3=3.8×10−5、β4=−4.3×10−5和β5=−5.8× 10−5，模型预测值与实际值分布和模型预测残差分别如图 4和图 5所示。对应的临界点拟合优度参数R20.997 8=和模型总体显著性检验的F值为5 033.15；Intercept、d2、d3、d22、d23及d2d3显著性检验的t分布分别为1 905.27、17.37、39.11、2.19、-1.18和−2.61；β0、β1、β2、β3、β4和β5满足95%置信度下的置信区间分别为β0=[9 328.872 3，9 348.518 0]、β1=[0.270 3，0.340 8]、β2=[0.914 3，1.013 0]、β3=[3.16×10−6，7.29×10−5]、β4=[− 0.000 12，3.04×10−5]和β5=[−0.000 1，−1.3×10−5]。对比线性模型和二次模型检验结果可知，二次模型拟合优度要比线性模型高，但差距在0.001以下；而线性模型的总体显著性和变量 Intercept、d2、d3的显著性要比二次型好，且对应的β0、β1和β2在95%置信度下的置信区间间隔要比二次型窄即β0、β1和β2准确度要比二次型高。

对应的安全域边界近似三次方模型为

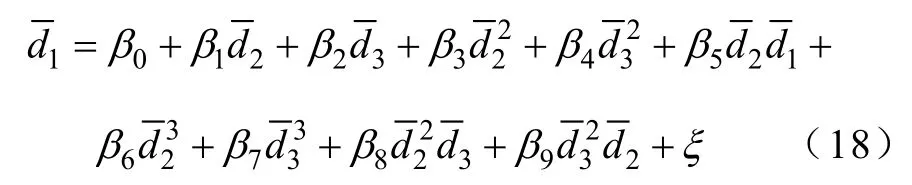
式中，各变量的回归系数分别为β0=9 342.876 7、β1=0.177 4、β2=0.998 0、β3=0.000 462、β4=−0.000 14、β5=−0.000 14、β6=−3.36×10−7、β7=1.08×10−7、β8= 1.11×10−7和β9=−3.94×10−8，模型预测值与实际值分布和模型预测残差分别如图6和图7所示。对应的临界点拟合优度参数20 9988 R.=和模型总体显著性检验的F值为4 687.3；Intercept、d2、d3、22d、23d、32d、33d、d2d3、223d d及232d d显著性检验的t分布分别为1 798.28、5.12、20.76、5.87、−0.86、−6.11、0.61、−1.45、1.53和−0.39；β0、β1、β2、β3、β4、β5、β6、β7、β8和β9满足95%置信度下的置信区间分别为

对比线性模型、二次模型的检验结果可知，三次模型的拟合优度要比线性模型和二次模型稍高，但三次模型的模型总体显著性、变量显著性及回归系数在 95%置信度下的置信区间间隔都较线性模型和二次模型差。

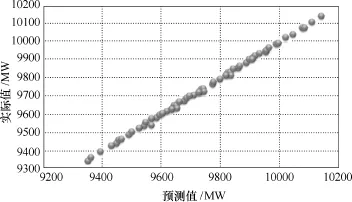
图6　三次模型下d1预测值与实际值在空间中分布Fig.6 Distribution of predicted values vs actual values for d1via cubic regression model

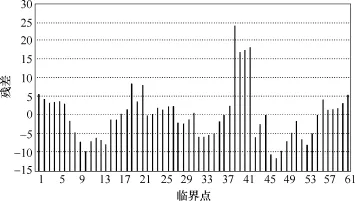
图7　三次模型下d1的残差Fig.7 Residual of d1via cubic regression model

以此类推，限于临界点个数，本文最后构建的回归模型最高阶次为10。随着模型阶次变化，模型拟合优度校验、模型总体显著性校验、变量显著性检验及回归系数在95%置信度下的置信区间的变化趋势如图8～图11所示。图中结果表明，随着模型阶次增加，模型的拟合优度逐步增加，模型总体显著性、变量显著性及95%置信度下回归系数的准确度显著性恶化，虽然模型的拟合优度趋于最优，但其变化范围仅在 0.002以下，效果并不显著。综合评估和分析图中热稳定安全域近似模型各项指标可知，对于上述各非线性回归模型而言，采用线性模型逼近安全域边界的结果最为理想，即在三维空间中在单一支路热稳定约束条件下，电力系统的热稳定安全域边界采用线性模型/超平面近似具有较高的拟合准确度。采用线性模型（超平面）逼近 YM热稳约束下的GD断面热稳定安全域边界的效果如图12所示，系统临界点均位于图中超平面HP中，未出现临界点远离 HP的现象，表明采用该超平面HP可高准确度逼近YM N−1约束下GD断面受YX 与TS出力影响下的热稳定安全域边界。

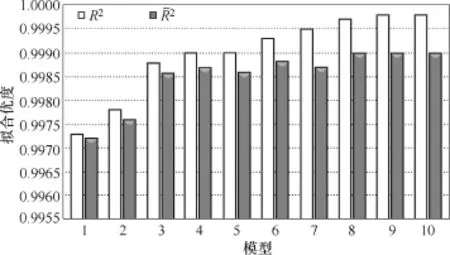
图8　拟合优度检验Fig.8 Goddesses of fit for different regression models

上述分析结果表明，在三维空间中，单一支路热稳定约束下的热稳定安全域边界可由超平面近似，而三维空间中任意一个超平面可由该平面上的三个坐标点确定。则在某一支路热稳定约束条件下，已知热稳定安全域边界上的三个临界点，则该安全域边界近似超平面可由上述三个临界点确定。利用上述特点可形成安全域边界近似超平面的快速计算算法，即通过所开发的极限计算软件，在搜索到单一热稳定约束下的安全域边界上三个临界点后，即可确定该安全域边界的近似超平面，大大减少了计算近似超平面的工作量。为降低所形成的安全域边界存在空洞的风险，在构建安全域时，可将所得超平面向下平移一段距离，以保留一定的安全裕度。

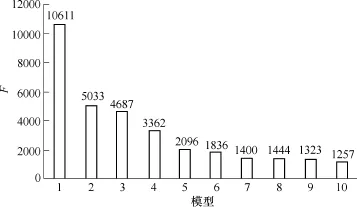
图9　模型显著性检验Fig.9 Test of significance for model with different regression models

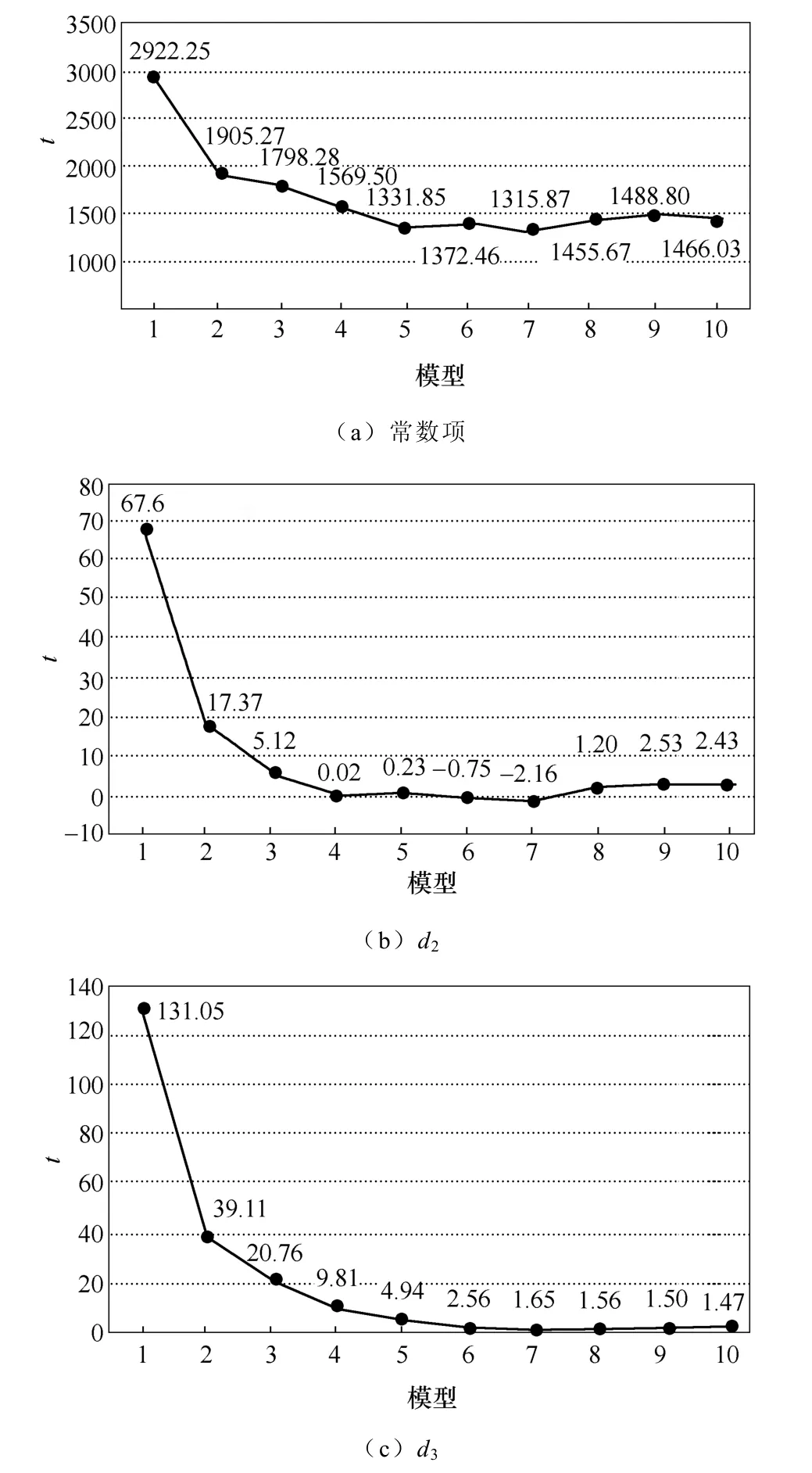
图10　变量显著性检验Fig.10 Test of significance for variables with different regression models

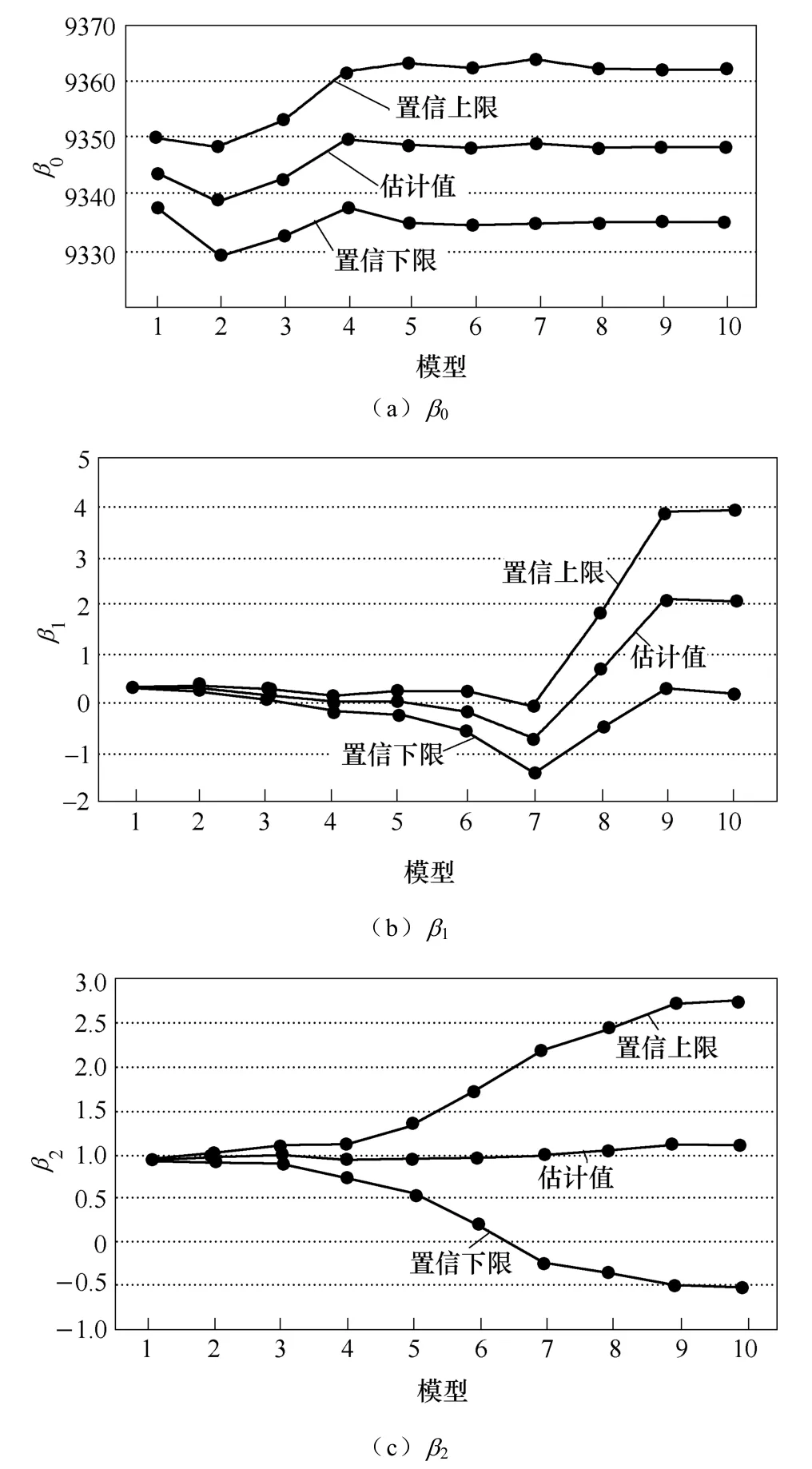
图11　回归系数的置信区间Fig.11 Confidence interval of regression coefficients with different regression models

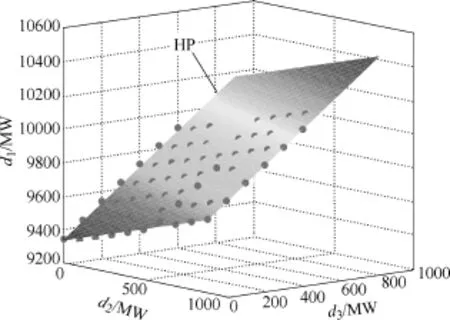
图12　超平面近似热稳定安全域边界的效果图Fig.12 Demonstration of hyperplane-approximated boundary of thermal security region

为验证该快速算法的有效性，本节采用 Monte Carlo对 sYM中的临界点抽样 4 000次形成4 000组临界点组合（每组中包含三个临界点），采用线性回归模型计算超平面的回归系数β0、β1和β2，再将sYM中所有临界点代入该超平面，通过式（9）的相对误差ε 和式（19）的相对角度/角度差θ 来评估该算法的有效性和可行性。计算结果分别如图 13和图 14所示，θ 最大的前20个抽样点计算结果见表1。

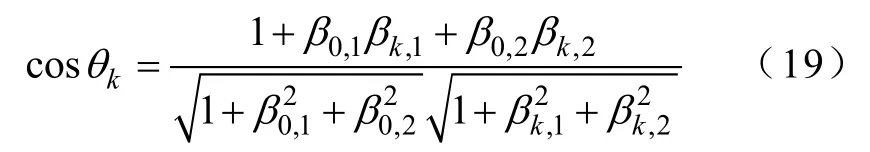
式中，β0,1和β0,2为采用 sYM中所有临界点计算得到的超平面回归系数；βk,1和βk,2为采用快速算法计算的超平面回归系数。

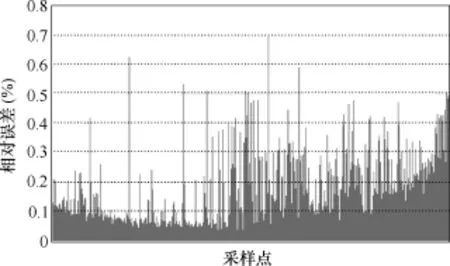
图13　相对误差Fig.13 Relative error

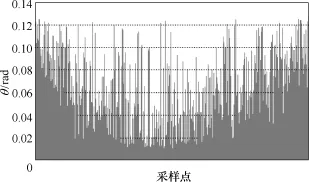
图14　角度差Fig.14 Angle difference

表1　θ 值最大的前20个超平面Tab.1 The top 20 hyperplanes with maximum θ

图13、图14及表1表明，采用快速算法所得到的超平面相比原方法误差极小，可满足安全域边界近似准确度要求。

4.2两热稳定约束下GD断面热稳定安全域构建

上述算例证明，在单一热稳定约束下，GD断面的热稳定域边界用线性回归模型近似可得到满意的近似效果。而对于同时存在两条联络线热稳约束下的安全域，其边界是否可以用同一个回归模型近似还需进一步验证。因此在上节基础上，本节进一步考虑 GD交流入口断面传输功率同时受 YM和MD约束下，YX与TS出力对断面极限的影响。类似上述方法构建安全域边界近似的线性模型，所得模型中各变量的回归系数分别为β0=9 466.533 2、β1=0.296 6和β2=0.441 6，模型预测值与实际值分布和模型预测残差分别如图15和图16所示。在d1、d2和d3所构成三维空间中，根据模型参数所得的安全域边界与临界点的分布如图17所示。对应的临界点拟合优度参数20.535 2 R=和模型总体显著性检验的F值为46；Intercept、d2和d3显著性检验的t分布分别为25.59、5.13和8.20；β0、β1和β2满足 95%置信度下的置信区间分别为β0= [9 393.397 8, 9 539.667 3]、β1=[0.185 5, 0.407 7]和β2=[0.334 1, 0.548 0]。

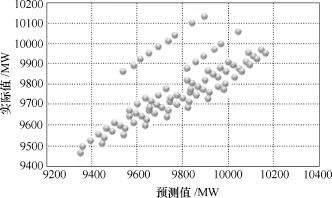
图15　单一超平面近似下d1预测值与实际值在空间中分布Fig.15 Distribution of predicted values vs actual values for d1via single hyperplane approximation

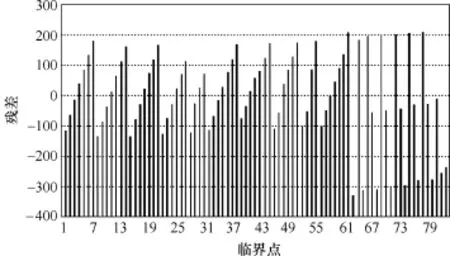
图16　单一超平面近似下d1的残差Fig.16 Residual of d1via single hyperplane approximation

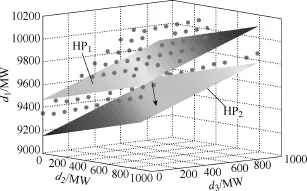
图17　直接拟合的热稳定安全域边界Fig.17 Security region boundary by direct fitting

从模型整体性评价指标及图15～图17可知，对于存在两个约束条件的热稳定域，其边界若只采用一个超平面拟合，其准确度显然不能满足要求（图17中 HP1），为保证安全域内部不存在空洞，需将该超平面向下平移到HP2位置，其保守性显而易见。借鉴上一节中一个约束边界采用一个线性模型逼近的思想，在两个约束的热稳定安全域中，对每个约束边界分别采用对应的线性模型分段逼近，即

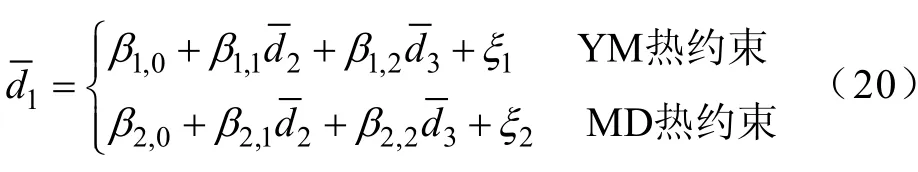
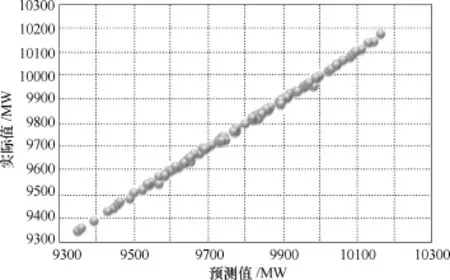
图18　超平面近似下d1预测值与实际值在空间中分布Fig.18 Distribution of predicted values vs actual values for d1via piecewise hyperplane approximation

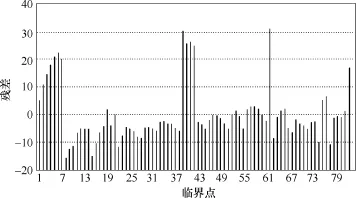
图19　两超平面近似下d1的残差Fig.19 Residual of d1via piecewise approximation

所得模型中各变量的回归系数分别为β1,0= 9 343.750 0、β1,1=0.322 4、β1,2=0.913 5、β2,0=11 380、β2,1=0.370 8和β2,2=−2.039 5，模型预测值与实际值分布和模型预测残差分别如图18和图19所示。在d1、d2和d3所构成三维空间中，根据模型参数所得的安全域边界近似效果及临界点在空间中分布如图20所示。YM热稳定约束下，对应的临界点拟合优度参数20 997 3 R.=和模型总体显著性检验的 F值为 10 611.4；Intercept、d2和 d3显著性检验的t分布值分别为2 922.25、67.61和131.05；β1,0、β1,1和β1,2满足 95%置信度条件下的置信区间分别为β1,0=[9 337.349 6, 9 350.150 4]、β1,1=[0.312 8, 0.331 9]和β1,2=[0.899 6, 0.927 5]。MD热稳定约束下，对应的临界点拟合优度参数20 997 6 R.=和模型显著性检验的F值为3 868.48； Intercept、d2和 d3显著性检验的 t分布值分别为581.04、44.46和−83.12；β2,0、β2,1和β2,2满足 95%置信度条件下的置信区间分别为β2,0=[11 339, 11 421]、β2,1=[0.353 4, 0.388 3]和β2,2=[−2.090 9, −1.988 2]。

对比分析分段近似前后模型的综合性评价指标及图 15～图 20可知，对于存在两个约束的热稳定安全域边界采用分段近似（即一个约束条件对应一个超平面）可得到满足要求的安全域边界逼近准确度。同理，对于存在 l条联络线热稳定约束下的热稳定安全域可采用式（21）模型求解安全域边界近似超平面。

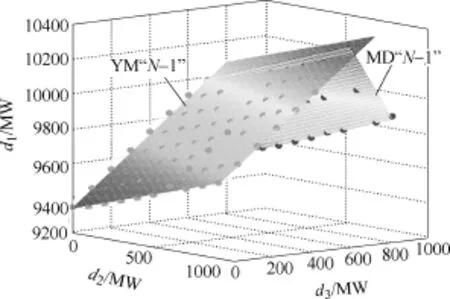
图20　分段拟合的热稳定安全域边界Fig.20 Security region boundary by subsection fitting

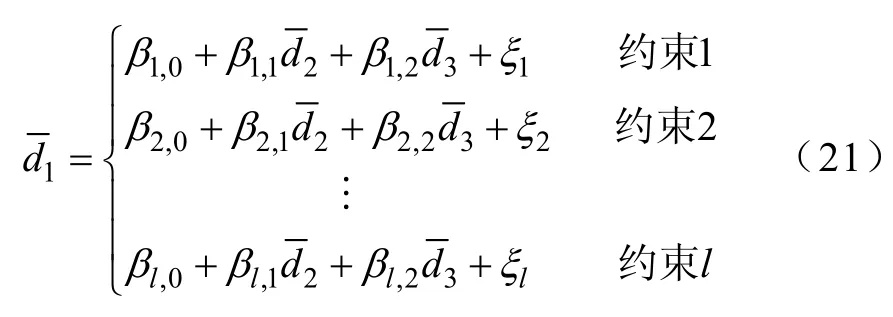
理论上，对安全域边界近似的超平面越多，其准确度越高，保守性越小，但随之带来计算量急剧上升，限制了热稳定安全域的在线应用。为兼顾计算准确度和效率，在实际应用中宜采用一个约束对应一个超平面的方案。但对这种方法的近似机理是本文下一阶段的研究重点。

4.3GD断面热稳定安全域

根据所开发的软件和所提的电力系统热稳定安全域边界近似算法，本节以CSG的GD受电断面为研究重点，采用PTDF确定影响该断面支路热稳定关键性电厂和区域为GPT、YX、TS和QBF[23]。在三维空间热稳定安全域中，以d1为GD断面传输的有功功率，d2与d3分别为YX与TS和QBF与GPT的有功出力，分别构建如图21所示的YX与TS出力配合下满足GD受电断面支路N−1热稳定约束下的GD断面热稳定安全域和如图22所示的QBF与GPT出力配合下的满足GD受电断面支路N−1热稳定约束下的GD断面热稳定安全域。

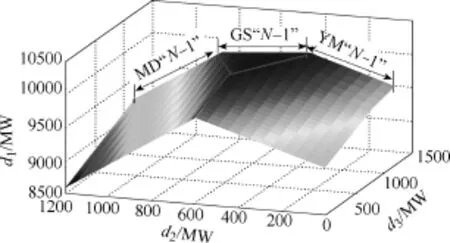
图21　YX与TS出力配合下的GD断面热稳定安全域Fig.21 Thermal security region of GD cross-section with cooperation of YX and TS

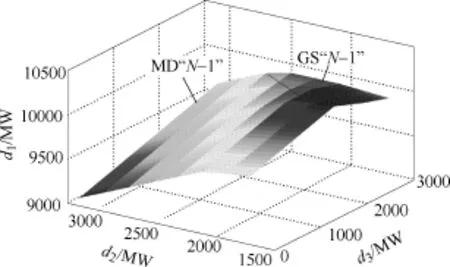
图22　QBF与GPT出力配合下的GD断面热稳定安全域Fig.22 Thermal security region of GD cross-section with cooperation of QBF and GPT

5 结论

本文基于非线性回归模型，探究了电力系统热稳定安全域边界的近似特性，通过构建多种安全域边界近似模型，从模型的拟合优度、模型总体显著性水平、变量显著性水平以及参数置信区间对所建模型进行全面、综合的评估，判定所提近似模型的可靠程度，确定合理的安全域边界近似模型。将所提方法应用到CSG，构建N−1约束下满足CSG关键送、受电断面热稳定约束的断面热稳定安全域，大量计算结果表明：

1）采用超平面近似电力系统的断面热稳定安全域边界合理、可行，可整体反映热稳定安全域边界特性，计算准确度高、实用性强。

2）在兼顾计算准确度和效率的条件下，对于存在多个热稳定约束的安全域，其边界宜采用超平面分段线性近似，即每个联络线热稳定约束边界采用一个超平面近似。

3）对于一个联络线热稳定约束边界，可采用一个超平面近似的特点，在实际应用时根据三维空间中三个临界点确定一个平面的理论，可开发出电力系统热稳定安全域边界在线快速近似算法。

4）采用本文所提方法构建的断面热稳定安全域准确度高、实用性强，可应用于跨区互联电网调度中心的EMS或WAMS中，在线监控系统的断面热稳定情况。

[1] Wu F F, Fu S. China’s future in electric energy[J]. IEEE Power and Energy Magazine, 2005, 3(4): 32-38.

[2] Wu F F, Zhong J, Zhang L. China’s energy and environment[J]. IEEE Power and Energy Magazine, 2006, 4(4): 20-31.

[3] Pawar N B. Definition and classification of power system stability[J]. IEEE Transactions on Power Systems, 2004, 19(2): 1387-1401.

[4] Joo S K, Kim J C, Liu C C. Empirical analysis of the impact of 2003 blackout on security values of U.S. utilities and electrical equipment manufacturing firms[J]. IEEE Transactions on Power Apparatus and Systems, 2007, 22(3): 1012-1018.

[5] Pourbeik P, Kundur P, Taylor C W. The anatomy of a power grid blackout-root causes and dynamics of recent major blackouts[J]. IEEE Power and Energy Magazine, 2006, 4(4): 22-29.

[6] Andersson G, Donalek P, Farmer R, et al. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance[J]. IEEE Transactions on Power Apparatus and Systems, 2005, 20(4): 1922-1928.

[7] Nayak R N, Soonee S K, Singh B, et al. The enquiry committee on grid disturbance in northern region on 30th July 2012 and in northern, eastern and north-eastern region on 31st July 2012[R]. New Delhi, 2012.

[8] 王成山, 李国庆, 余贻鑫, 等. 电力系统区域间功率交换能力的研究(二): 最大交换功率的模型与算法[J]. 电力系统自动化, 1999, 23(4): 5-9. Wang Chengshan, Li Guoqing, Yu Yixin, et al. Study on transmission transfer capability of interconnected electric power systems(II): model and algorithm for calculating maximal transmission power[J]. Automation of Electric Power Systems, 1999, 23(4): 5-9.

[9] 李国庆, 姚少伟, 陈厚合. 基于内点法的交直流混合系统可用输电能力计算[J]. 电力系统自动化, 2009, 33(3): 35-39. Li Guoqing, Yao Shaowei, Chen Houhe. Available transfer capability calculation for hybrid AC/DC systems based on interior point method[J]. Automation of Electric Power Systems, 2009, 33(3): 35-39.

[10] 李响, 郭志忠. 基于N−1原则的输电断面传送功率能力分析[J]. 电力系统自动化, 2004, 28(9): 28-30, 35. Li Xiang, Guo Zhizhong. Analysis of network transmission capability based on N−1 principle[J]. Automation of Electric Power Systems, 2004, 28(9): 28-30, 35.

[11] 李鹏, 苏寅生, 李建设, 等. 多维安全域下南方电网的方式计算探讨[J]. 南方电网技术, 2011, 5(6): 7-15. Li Peng, Su Yinsheng, Li Jianshe, et al. On the operation planning of china southern power grid with security region in multi-dimension spaces[J]. Southern Power System Technology, 2011, 5(6): 7-15.

[12] 余贻鑫. 电力系统安全域方法研究述评[J]. 天津大学学报, 2008, 41(6): 635-646. Yu Yixin. Review of study on methodology of security regions of power system[J]. Journal of Tianjin University, 2008, 41(6): 635-646.

[13] Makarov Y V, Lu S, Guo X, et al. Wide area security region final report[R]. PNNL-19331, Washington DC, USA: U.S. Department of Energy, 2010.

[14] 王菲, 余贻鑫. 基于广域测量系统的电力系统热稳定安全域[J]. 中国电机工程学报, 2011, 31(10): 33-38. Wang Fei, Yu Yixin. Power system thermal security region based on wide area measurement system[J]. Proceedings of the CSEE, 2011, 31(10): 33-38.

[15] Makarov Y V, Du P, Lu S, et al. PMU-based wide-area security assessment: concept, method and implementation[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 1325-1332.

[16] Yu Y X. Direct method for voltage and transient stability regions (final report), ID 1010553[R]. Palo Alto, CA, USA: EPRI, 2005.

[17] 余贻鑫, 冯飞. 电力系统有功静态安全域[J]. 中国科学: A辑, 1990, 33(6): 664-672. Yu Yixin, Feng Fei. Active power steady-state security region of power system[J]. Science in China: Series A, 1990, 33(6): 664-672.

[18] 余贻鑫, 曾沅, 冯飞. 电力系统注入空间动态安全域的微分拓扑特性[J]. 中国科学: E辑, 2002, 32(4): 503-509. Yu Yixin, Zeng Yuan, Feng Fei. Differential topological characteristics of the DSR on injection space of electrical power system[J]. Science in China: Series E, 2002, 32(4): 503-509.

[19] 曾沅, 樊纪超, 余贻鑫. 电力大系统实用动态安全域[J]. 电力系统自动化, 2001, 25(16): 6-10. Zeng Yuan, Fan Jichao, Yu Yixin. Practical dynamic security regions of bulk power systems[J]. Automation of Electric Power Systems, 2001, 25(16): 6-10.

[20] 赵金利, 余贻鑫, 贾宏杰. 电力系统割集空间静态电压稳定域的可视化及实现[J]. 电力系统自动化, 2005, 29(5): 56-61. Zhao Jinli, Yu Yixin, Jia Hongjie. Visualization of the static voltage stability region in cut-set space of power systems[J]. Automation of Electric Power Systems, 2005, 29(5): 56-61.

[21] 中国南方电网电力调度控制中心. 中国南方电网二〇一三年运行方式[R]. 广州: 中国南方电网有限责任公司, 2013.

[22] Jiang Tao, Jia Hongjie, Jiang Yilang, et al. Cutsetangle based wide area thermal security region and its application in China southern power grid[J]. International Transactions on Electrical Energy Systems, 2014, 24(11): 1600-1617.

[23] 天津大学. 南方电网多维空间安全域的边界性质及其实用算法研究[R]. 天津: 天津大学, 2013.

Approximating Method of Wide Area Thermal Security Region Boundary in Bulk Power System

Jiang Tao1Jia Hongjie1Jiang Yilang1Kong Xiangyu1Lu Ning2
（1. Key Laboratory of Smart Grid of Ministry of Education Tianjin University Tianjin 300072 China 2. Department of Electrical and Computer Engineering NC State University Raleigh 27695-791 U.S.）

In this paper, approximating approaches are investigated for wide-area thermal security region boundary (SRB) in large-scale power system with N−1 criterion through multivariate nonlinear regression theory. Multivariate nonlinear regression theory is adopted to construct various multivariate nonlinear regression models for fitting SRB. Goodness of fit, significance level for model, significance level for variable and confidence intervals for regression coefficient are employed to comprehensively assess the reliability of the proposed approximating model and determine the appropriate model for fitting SRB. A realistic large-scale power system is utilized to validate and evaluate the various proposed models with massive scenarios, and then an appropriate model for fitting SRB is determined. With this appropriate model, a rapid algorithm for fitting SRB is developed, and the approximating approach for SRB with multiple N−1 constraints is also investigated. The proposed approach is further applied to the realistic large-scale power system to form a wide-area thermal security region for cross-section with multiple N−1 constraints. The results verify the proposed model.

Power system, N−1, thermal stability, security region, nonlinear regression model

TM712

姜 涛 男，1983年生，博士研究生，主要研究方向为电力系统安全性与稳定性、新能源集成。

E-mail: electricpowersys@163.com

贾宏杰 男，1973年生，博士，教授，博士生导师，主要研究方向为电力系统安全性与稳定性、配电系统规划、智能电网。

E-mail: hjjia@tju.edu.cn（通信作者）

国家自然科学基金（51277128、51377118）和南方电网科技项目（K-ZD2012-006）资助。

2014-03-26 改稿日期 2014-09-01