一种基于磁组合式变压器的AC-DC高频变换器

李春杰黄文新李 朋樊长鑫

（1. 南京航空航天大学自动化学院 南京 211106 2. 中国人民解放军94672部队 南京 211100）

一种基于磁组合式变压器的AC-DC高频变换器

李春杰1黄文新1李 朋2樊长鑫1

（1. 南京航空航天大学自动化学院 南京 211106 2. 中国人民解放军94672部队 南京 211100）

为了提高大功率开关电源的功率因数和可靠性，提出了一种基于磁组合式变压器的AC-DC变换器。该结构的变换器是将三个耦合变压器磁心中产生的磁通叠加输出，而非电的形式输出。根据三相电路瞬时功率平衡原理，利用三相互差120°的交流电的特性，使该变换器的直流环节的滤波电容采用了薄膜电容，而非电解电容，使电网侧的输入电流正弦化，实现自然PFC功能，从而提高了功率因数和功率密度。仿真和一台1kW的原理实验样机验证了理论分析的正确性及变换器的可行性。

磁通叠加 磁组合式变压器 薄膜电容 自然PFC

0 引言

电力电子技术的发展带动了电源技术的发展，通信、电子检测设备电源、军事装备、交通设施和工业设备等领域都已广泛使用了开关电源，取得了显著的经济效益和社会效益。探索具有高可靠性、高功率因数和高功率密度的新型开关电源技术具有重要意义。

在充电站、服务器电源等应用场合的 AC-DC变换器，由于整流二极管的非线性和滤波电容的储能作用，造成输入电流畸变，严重污染电网。目前，各国都很重视这点，并陆续出台相关法规，对进入电网的设备，严格规定其输入功率因数和电流谐波分量。为了改善功率因数，引入了PFC技术。一种实施方法就是在交流电网输入经二极管整流之后，先不接大容量的滤波电容，而是插入一个Boost型开关变换器，该变换器使输入电流平均值能自动跟随全波整流电压基准，并维持直流输出电压稳定。同时使输入电流、电压波形均为正弦低频波形，且相位相同，从而抑制了严重的谐波干扰。另一种就是PWM 整流器[1,2]，它具有简单的结构和较高的功率因数，但是输入、输出级无电气隔离。这两种方法可使功率因数升到0.99左右，甚至接近1。但是，给电器设备带来了附加成本及复杂的控制，第一种PFC电路的插入使系统效率有所下降。为了提高效率，简化控制，单级PFC电路被提出。对于开关电源来说，除了提高功率因数外，可靠性和寿命也是主要考虑的因素。从开关电源可靠性角度分析可知，电解电容的使用寿命和主要元器件的电压应力影响开关电源的可靠性。

在中大功率应用场合，为了解决电压、电流应力，文献[3]采用了多模块级联的方式，但是该结构存在均压、均流的问题，控制方法复杂，并且含有成本较高、体积较大的电解电容。为了提高开关电源的可靠性、功率因数和功率密度，文献[4-6]提出了一种模块化的三相 AC-DC高频变换器，它适用于低压、中功率场合，该变换器在不控整流电路后面加入了Cuk、Sepic等斩波电路，这种拓扑结构易于实现自然PFC功能。为了简化两级复杂的控制以及提高功率密度，文献[4,7,8]能够实现单级PFC功能，以上的高频变换器都是将不同的源以电能量的形式相结合输出。文献[5]提出了一种三相组合式的AC-DC变换器，它采用了三个独立的高频变压器，而三个高频变压器二次绕组直接串联再整流输出的结构形式。

本文针对中大功率 AC-DC变换器应用场合提出了一种基于磁组合式变压器且具有单级PFC功能的 AC-DC变换器。它与文献[5]的最大区别，就是本文采用了三个一次绕组单输出的磁组合变压器。该变换器采用了以磁能量的形式叠加输出；该变换器根据三相电路瞬时功率平衡原理，利用其三相交流电互差120°的特性，减小了滤波电容的容值，使用薄膜电容，省去了电解电容，提高了变换器的可靠性、功率因数和功率密度；该拓扑结构降低了主要开关器件的电压应力，可以实现自然PFC功能。

1 基于磁组合式变压器的AC-DC高频变换器拓扑结构和原理分析

1.1AC-DC高频变换器的结构

基于磁组合式变压器的三相 AC-DC高频变换器结构如图1所示，包括三个完全相同的单相输入功率变换模块（LC滤波电路、二极管不可控整流电路和高频逆变器）、一个三相组合式高频变压器和一个不可控整流滤波电路，其中，三个单相输入电源为互差120°的三相交流电，接线方式较灵活，既可以是星形联结，也可以是三角形联结。根据三相电路整体功率平衡的原理，利用互差120°的特性，可以降低每个单相整流电路的滤波电容值，采用薄膜电容，而非电解电容，实现自然PFC功能。三相组合式高频变压器的三路一次绕组分别连接三个完全相同的变换器模块，而二次绕组与输出的整流电路相连，输出恒定的电压。

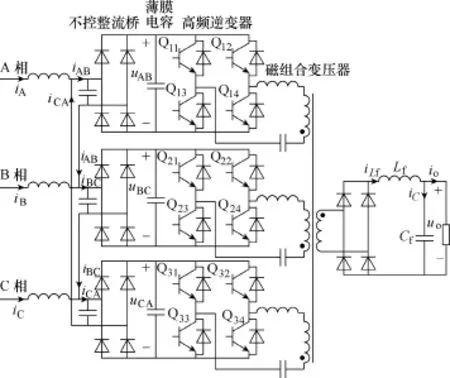
图1　基于磁组合式变压器的AC-DC变换器Fig.1 AC-DC converter based on magneticcombination transformer

1.2输入侧的不可控整流电路

设输入三相幅值相等，互差120°的交流电的线电压为

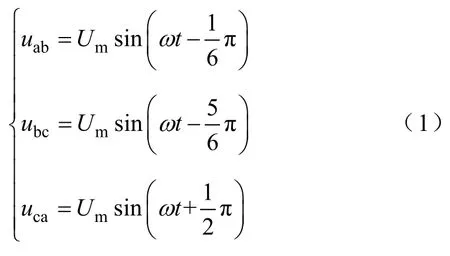
式中，mU三相交流电的线电压峰值。经不可控整流滤波电路得到

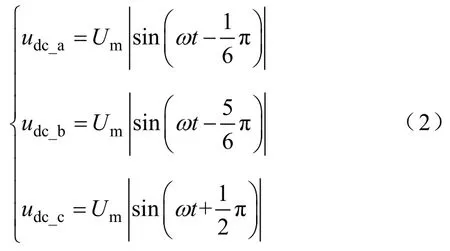
不可控整流桥输出侧并联了薄膜电容，使得直流母线上的电压为式（2）所示的脉动直流电压，波形为馒头波。只有当直流母线电流和直流母线电压波形相同时，才能使电网输入电流为正弦波，实现自然PFC功能。只要对全桥逆变器进行SPWM调制，则直流母线电流基波可表示为

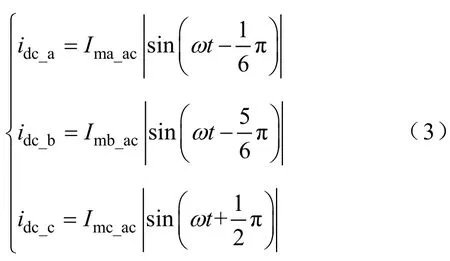
1.3全桥逆变电路

通过SPWM调制，在一个开关周期内，导通时间为Ts/2时，高频逆变器输出电压为

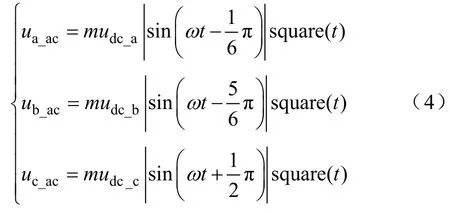
式中，m为调制系数，01m≤≤ ；square(t)为方波函数，其峰-峰值为2，频率为开关频率fs。

假设逆变器输出电压与电流的相位差很小，可以忽略不计，则逆变器输出电流为

在不考虑损耗情况下，根据变换器输入功率等于输出功率[2]，可得出直流母线电流表达式如式（3）所示。

1.4磁组合变压器的结构和原理分析

三相组合式高频变压器制作结构剖面如图2所示。三相组合式高频变压器的三路一次绕组绕制在相互独立的三组完全相同的 EE型磁心的中柱上，每个磁心中磁通脉动的大小取决于各相波动的整流输入电压，而二次绕组匝链三组磁心的中柱，二次侧输出电压由二次绕组匝链三相组合式高频变压器的三个磁心磁通感应输出，三个磁通叠加后峰谷相抵，从而达到了减小输出电压脉动的目的。

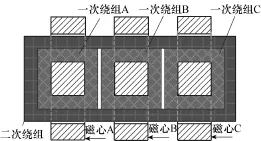
图2　磁组合变压器的结构剖面图Fig.2 Cross-section of magnetic-combination transformer

忽略绕组漏感，由图2所示的结构图可得出磁组合变压器A相绕组等效磁路模型，如图3所示。B、C相等效磁路模型与A相类似。其中为一组EE型磁心的两个边柱合并成一路的磁阻为一组EE型磁心的中柱上的磁阻和分别为一次绕组电流和在磁心中产生的主磁通；φ为总磁通和为一次绕组A、B和C的匝数。

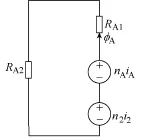
图3　一路简化的等效磁路Fig.3 Simplified equivalent magnetic model

根据安培环路定律， 磁组合变压器的磁路表达式为[9]

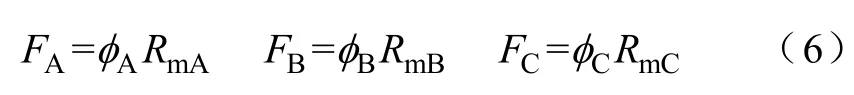
根据电磁感应原理，由式（4）可知不含有直流分量的逆变器输出电压，可得其中一相磁通的表达式为

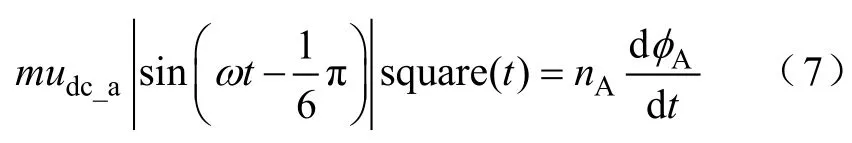
由式（7）可以看出，磁组合变压器的主磁通是按照正弦规律变化的。所以，磁组合变压器一次侧的三个主磁通所产生的磁动势按照正弦规律进行变化，而这三路磁动势叠加后为一恒定磁动势。负载作用在主磁路上的全部磁动势也为一恒定磁动势，从而实现变压器磁动势平衡。

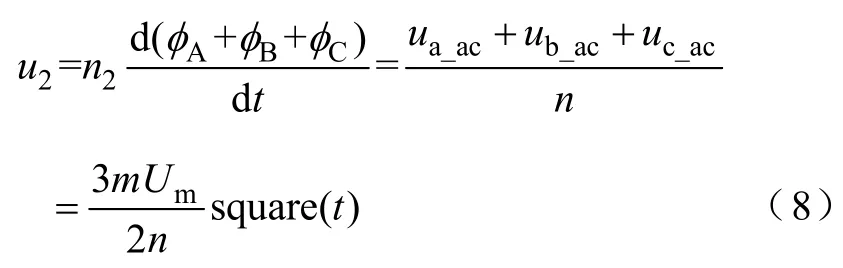
式中，n为匝比，n=nA/n2=nB/n2=nC/n2。

1.5磁组合变压器的等效电路模型

根据电磁感应定律，基于理想情况下，忽略一次绕组内阻，一次绕组端电压方程为

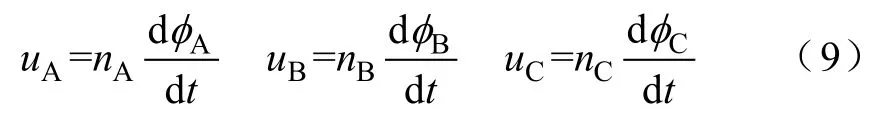
由式（6）和式（9）可得

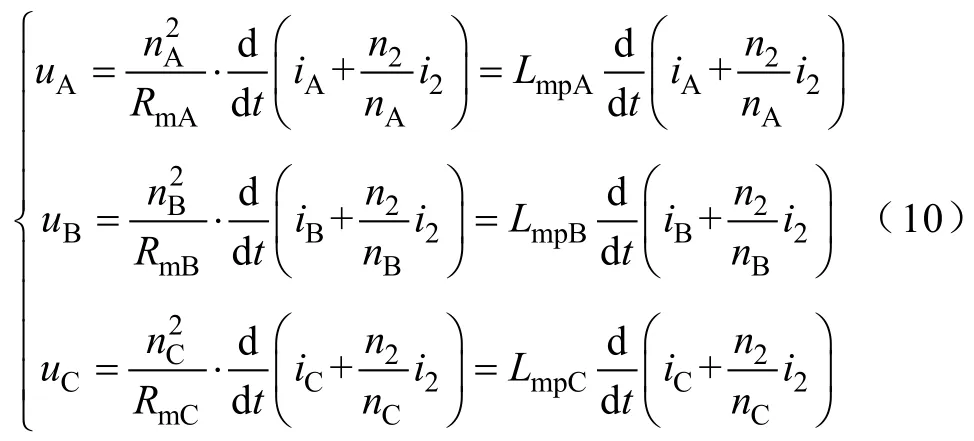
式中，LmpA、LmpB和LmpC分别为一次绕组的励磁电感。

考虑一次侧漏感（L1A、L1B、L1C）、二次侧漏感（Ll2）的情况下，一次、二次绕组端电压方程为

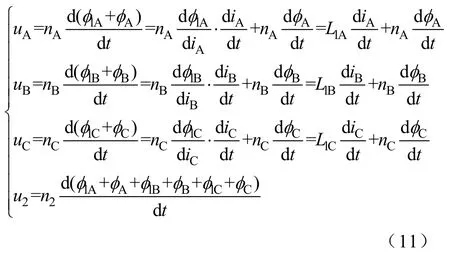
由式（9）～式（11）可得

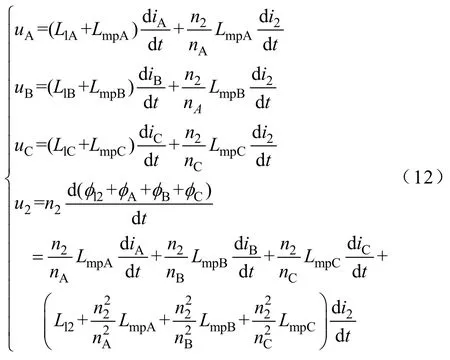
一次、二次侧绕组端电压和电流之间的关系写成矩阵形式为

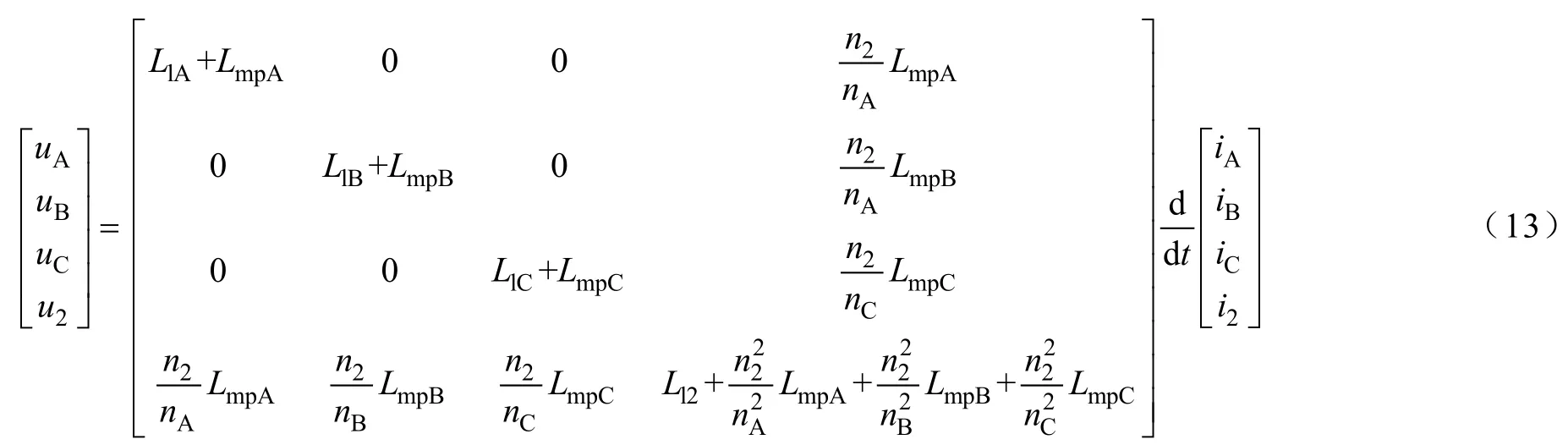
由式（12）和式（13）得出磁组合变压器的等效电路模型，如图4所示。

1.6磁组合变压器的数学模型

根据 1.4节所述的磁组合式变压器的结构，用于一般的高频变压器的建模方式不能很好体现出磁组合变压器的磁路特性。本文从一次、二次侧电压方程和磁链方程入手，采用状态变量法建立理想磁组合变压器的数学模型。

考虑一次、二次绕组内阻压降，一次、二次绕组端电压方程为[10]

图4　考虑变压器励磁电感和一次、二次侧漏感的等效电路模型Fig.4 The equivalent circuit model considering magnetizing inductance and leakage inductance of transformer

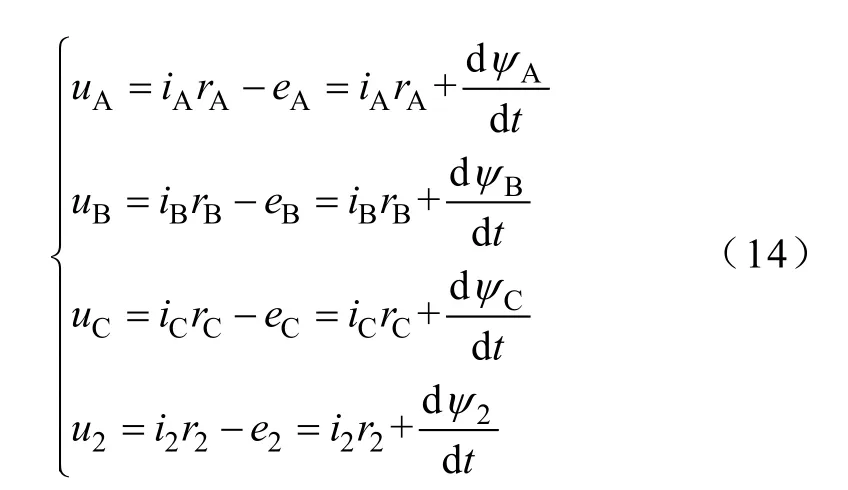
相应的磁链方程为

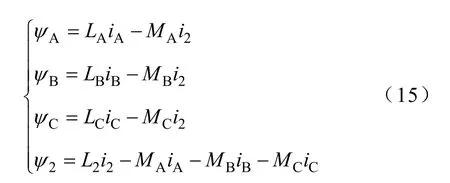
式中，MA、MB和MC为一次绕组A、B和C分别和二次绕组之间的互感；rA、rB、rC和 r2为一次绕组内阻。

由式（15）可得

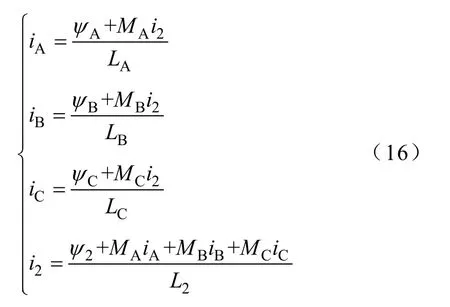
则由式（14）、式（16）联立可得

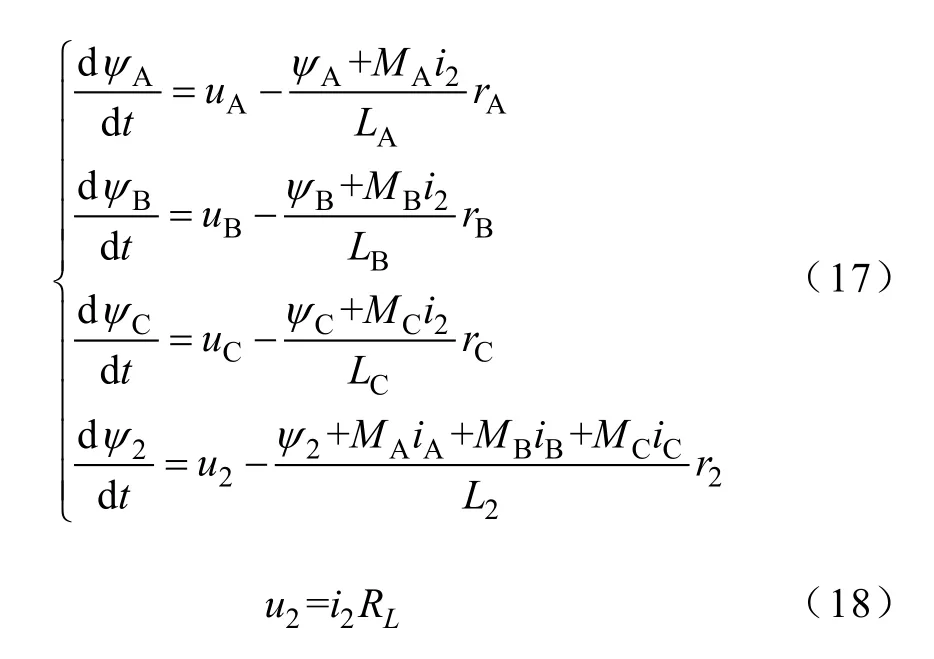
式（16）～式（18）构成了组合式变压器的动态模型，在此模型中，磁链作为中间变量，一次、二次绕组端电压作为输入变量，一次、二次绕组电流作为输出变量。

2 调制方法分析

本文采用按照正弦规律变化的移相控制方式[11,12]，在该移相控制方式中，每个桥臂的两只开关管均为180°互补导通，两个桥臂的开关信号之间存在一个相移，通过控制这个按照正弦规律变化的相移角来控制逆变桥的输出电压脉宽的大小，从而控制输出电压。

电力电子变换器的高频变压器内部的磁通在开关脉冲电压作用下，通常表现为三种变化形态：正向施加电压磁通增长、反向施加电压磁通降低和自由续流磁通基本不变。根据组合变压器的单输出绕组磁通耦合工作原理，二次绕组匝链了三个磁心中的磁通，所以三个一次绕组在磁心中产生的磁通变化方向必须基本相同，这样输出绕组匝链三路磁心的磁通变化而产生的感应电动势相互叠加而非相互抵消，以保证输出电动势的要求。因此，三单相全桥电路要同步控制。在电网电压条件下，给出了驱动信号波形以及主要电压波形，如图5所示。其中，ua_ac、ub_ac和 uc_ac为三个高频逆变桥的输出电压波形， u2为磁组合变压器的二次绕组电压波形。可以看出二次电压为3个一次电压叠加之和。

3 AC-DC变换器仿真和实验分析

本文采用Matlab仿真软件。根据1.6节所述的数学模型建立磁组合式变压器的仿真模型。根据第2节的控制方式建立系统仿真模型。

仿真参数：输入电压为互差120°幅值为311V的三相交流电，三相三线制三角形联结，负载为5Ω，输出电压为180V，开关频率为12kHz，变压器一次绕组自感 LA=LB=LC=10mH，二次绕组自感 L2= 6mH，互感MA=MB=MC=4.5mH。从图6可以看出，输入电流的正弦度很高，而且和电网电压相位一致。图7为输入电流的频谱分析，从图中可以得出输入电流的总畸变系数THD约为6%，功率因数在0.99以上。图8所示为直流母线电压，其波形为馒头波。图9为全桥逆变器的输出电压，从图9可以看出在一个开关周期中，正、负半轴的电压值相等，输出电压的平均值为零，而且逆变器输出电压的包络线为直流母线电压波形。逆变器输出电压的宽度按照正弦规律变化。图10给出了高频变压器一次、二次电流的仿真波形展开图，可以看出3个一次电流相等，而二次电流与一次电流之间有个匝比关系。图11为输出电压波形，可以看出一个电源周期有6个较小波动，二次绕组的输出电压是磁组合变压器的3个一次电压叠加后峰谷相抵的结果。

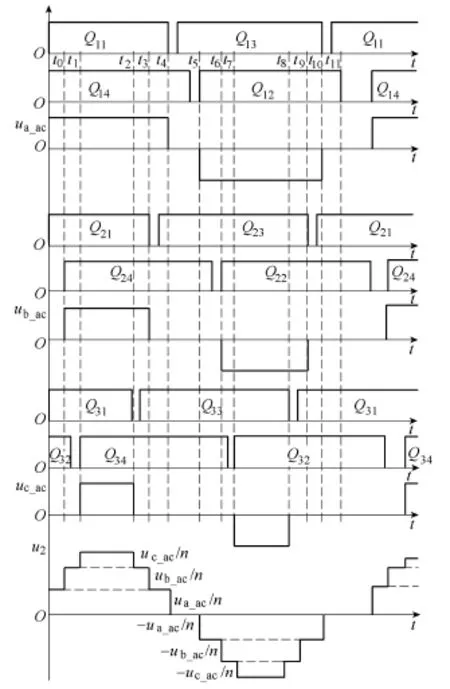
图5　驱动信号波形以及变压器一次、二次电压波形Fig.5 Waveforms of gate driving signals and the primaryside voltage and the secondary-side voltage of transformer

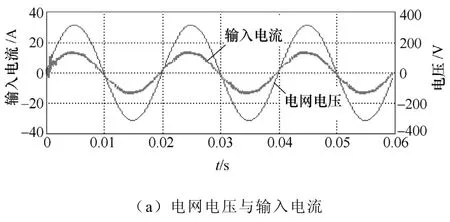
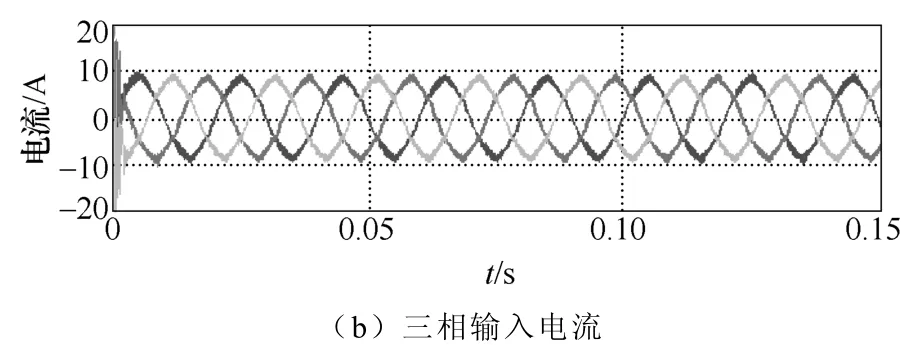
图6　电网电压与输入电流仿真Fig.6 Input voltage and current simulation waveforms

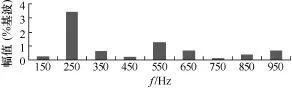
图7　A相输入电流的频谱Fig.7 Input current frequency spectrum simulation of phase A

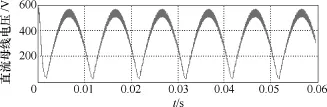
图8　A相直流母线电压仿真波形Fig.8 DC-link voltage simulation waveform of phase A

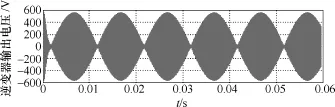
图9　A相高频变压器的输入电压仿真波形Fig.9 Input voltage simulation waveform of phase A of high frequency transformer

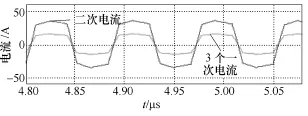
图10　高频变压器3个一次电流及二次电流仿真波形Fig.10 The primary-side current and secondary-side current simulation waveforms of high frequency transformer

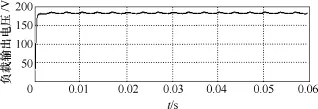
图11　负载输出电压仿真波形Fig.11 Output voltage simulation waveform

在理论分析和仿真研究基础上，根据如图1所示的拓扑结构以及图5所示的驱动信号，本文设计了一台功率为 1kW，输出电压为 100V，开关频率为12kHz，输入滤波电感为500 μH，直流母线滤波电容为2 μF，磁组合变压器匝比为48∶18的样机进行原理实验验证。图12依次给出了网侧输入电压、电流波形、直流母线电压波形（馒头波）、磁组合变压器一次绕组电压波形以及输出电压的波形。经测试输入电流的 THD在 10%之内，功率因数能达到0.99以上，该拓扑结构能实现自然PFC功能。实验结果验证了磁组合变压器的仿真模型的正确性以及理论分析的正确性。

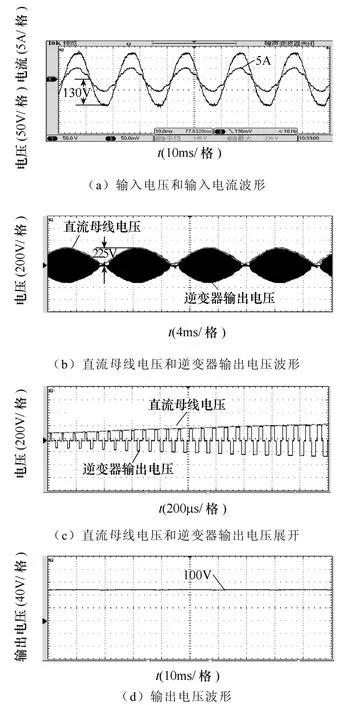
图12　实验波形Fig.12 Experimental waveforms

4 结论

本文提出了基于磁组合变压器的三相 AC-DC高频变换器。该拓扑结构是通过磁组合变压器将三个脉动的功率叠加成恒定的功率。该变换器具有以下主要特点：①该变换器采用了模块化结构形式，使得电压应力减小；②该变换器直流母线上的滤波电容采用数微法的薄膜电容，而非电解电容，而且体积相应减小；③该变换器可以实现自然PFC功能；④该变换器引入了三输入绕组、单输出绕组的磁组合变压器，将变换器的输入级和输出级耦合在一起，使 AC-DC变换器直接以耦合磁能的形式叠加而非独立输出后再以电路的形式叠加输出，可简化电路结构。

[1] 高吉磊, 林飞, 郑琼林. 基于网压预测的单相PWM 整流器比例谐振控制[J]. 电工技术学报, 2011, 26(5): 45-51. Gao Jilei, Lin Fei, Zheng Qionglin. Proportionalresonant control of single-phase PWM rectifiers based on grid voltage prediction[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 45-51.

[2] 李和明, 朱晓荣, 石新春, 等. 电流型 PWM 整流器的不平衡控制[J]. 电工技术学报, 2010, 25(7): 86-92. Li Heming, Zhu Xiaorong, Shi Xinchun, et al. A control scheme of current-source PWM rectifier under unbalanced supply conditions[J]. Transactions of China Electrotechnical Society, 2010, 25(7): 86-92.

[3] 张容荣, 阮新波, 陈武. 输入并联输出串联变换器系统的控制策略[J]. 电工技术学报, 2008, 23(8): 86-90. Zhang Rongrong, Ruan Xinbo, Chen Wu. Control strategy for input-parallel output-series converter systems[J]. Transactions of China Electrotechnical Society, 2008, 23(8): 86-90.

[4] Hamdad F S, Bhat A K S. Three-phase single-stage AC/DC Boost integrated series resonant converter[J].IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(4): 1311-1321.

[5] Kim M, Yoo A, Sul S K. A new universal isolated converter for grid connection[J]. IEEE Transactions on Industry Applications, 2012, 48(2): 685-695.

[6] Kamnam U, Chunkag V. Analysis and design of a parallel CUK power factor correction circuit based on power balance control technique[J]. IEEE Transactions on Industry Applications, 2006, 126(5): 533-540.

[7] Wang C M, Lin C H, Liu C H, et al. High performance single-stage transformer-isolated AC/DC converter[C]//IEEE Transactions on Power Electronics Conference, Sapporo, 2010: 131-136.

[8] Yoo K M, Kim K D, Lee J Y. Single and three-phase PHEV onboard battery charger using small link capacitor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3136-3144.

[9] 杨玉岗. 现代电力电子的磁技术[M]. 北京: 科学出版社, 2001.

[10] 索南加乐, 许立强, 焦在滨, 等. 基于磁路特性的三相三柱式变压器的数学模型及等效电路[J]. 电力系统自动化, 2011, 35(15): 52-54. Suonan Jiale, Xu Liqiang, Jiao Zaibin, et al. Mathematical model and equivalent circuit for three-phase three-limb transformer[J]. Automation of Electric Power Systems, 2011, 35(15): 52-54.

[11] 阮新波. 脉宽调制DC/DC全桥变换器的软开关[M].北京: 科学出版社, 2012.

[12] 赵涛, 王相綦, 尚雷. 基于移相全桥技术的 PFC三相四线 AC/DC 变换器[J]. 电工技术学报, 2004, 19(4): 70-75. Zhao Tao, Wang Xiangqi, Shang Lei. A novel threephase four-wire AC/DC PFC converter based on PSFB technique[J]. Transactions of China Electrotechnical Society, 2004, 19(4): 70-75.

An AC-DC High Frequency Converter Based on Magnetic-Combination Transformer

Li Chunjie1Huang Wenxin1Li Peng2Fan Changxin1
（1. Nanjing University of Aeronautics and Astronautics Nanjing 211106 China 2. The Chinese People’s Liberation Army 94672 Troops Nanjing 211100 China）

To improve power factor and reliability of AC power supply, an AC-DC power converter based on magnetic-combination transformer is proposed in this paper. Instead of input AC sources in electric form, the proposed converter combines input AC source in magnetic form by adding up the produced magnetic flux from three magnetic cores of the coupled transformers. According to the instantaneous power balancing principle of three-phase circuit and the mutual difference of 120° for three-phase AC source, this topology adopts film capacitor and makes input current sinusoidal. This converter can achieve spontaneous PFC and improve power factor and power density. The simulation and experimental prototype of 1kW verify the theoretical analysis and the feasibility of the converter.

Magnetic flux additivity, magnetic-combination transformer, film capacitor, spontaneous PFC

TM461

李春杰 女，1985年生，博士研究生，主要从事电力电子与电力传动方面的研究。

E-mail: lcj_85@163.com（通信作者）

黄文新 男，1966年生，教授，博士生导师，主要从事功率电子学与电机控制方面的研究。

E-mail: huangwx@nuaa.edu.cn

江苏省普通高校研究生科研创新计划项目（CXLX13_153）和中央高校基本科研业务费专项资金项目资助。

2014-04-17 改稿日期 2014-07-01