一种适用于新能源并网的谐振升压变换器
陈 武 吴小刚 蒋 玮 胡仁杰
(东南大学江苏省智能电网技术与装备重点实验室 南京 210096)
一种适用于新能源并网的谐振升压变换器
陈 武 吴小刚 蒋 玮 胡仁杰
(东南大学江苏省智能电网技术与装备重点实验室 南京 210096)
谐振变换器由于可实现开关器件的软开关而十分适用于高压大功率场合。由此提出了一种适用于新能源并网应用场合的谐振升压变换器,该变换器利用 LC并联谐振网络可实现很高的电压增益,同时具有开关管零电压开通和近似零电压关断以及整流二极管零电流关断的优点。此外,相比于传统谐振变换器,该变换器在整个负载范围内开关频率变化范围小。阐述了该变换器的工作原理和工作特性,讨论了谐振网络参数的选择,给出了具体的控制电路,并通过一台100V/1kV、1kW的原理样机验证了该变换器的工作原理,最后给出实验结果。
谐振变换器 升压 新能源 软开关
0 引言
随着化石能源的日益枯竭和环境恶化问题的日益加剧,我国乃至世界各国纷纷都将发展新能源提升至前所未有的高度。目前,绝大部分新能源都以交流电形式馈入电网,而新能源发电装置以及储能设备一般均含有直流环节,需经过直-交逆变环节接入电网,增加了较多的电能损耗。其次,各种新能源如风能、太阳能、海洋能等都具有间歇性、随机性特点,而大规模新能源接入电网对传统的电力装备、电网结构和运行技术等都提出了严峻考验。直流电网技术作为解决上述问题众多方案中的一种,逐渐成为研究热点[1-3]。
目前,新能源发电装置的直流环节电压都比较低,需要通过直流升压变换器接入高压直流电网,而作为各种新能源与高压直流电网连接的桥梁,直流升压变换器不仅是电能的传输者,同时又是抑制多种故障情况的缓冲/隔离者,起到了交流电网中升压变压器的作用,是直流电网的核心部件之一[4,5]。
目前国外对于新能源并网用的直流升压变换器研究正日益深入,而国内还处于起步阶段。Converteam公司研究人员提出了以Boost变换器来实现±50~±200kV电能传输的方案[6]。但 Boost变换器的开关损耗和二极管反向恢复损耗都较大,导致变换效率较低,且Boost 变换器一般用于电压增益小于6 的场合[7]。美国德州农工大学Enjeti教授提出了一种将Boost变换器和Buck-Boost变换器的输出电压相串联以得到高电压增益的方案[8],每个变换器提供一半的输出电压和输出功率,开关管和二极管的电压、电流应力都相应减小,并对1MW、5.7kV/132kV变换器进行了评估,但该变换器同样存在开关损耗和二极管反向恢复损耗较大的问题。东南大学陈武等则对基于中压直流母线海上风电系统中的升压直流变换器拓扑进行了比较,并提出了一种谐振开关电容变换器[9,10],可较好地避免开关损耗和二极管反向恢复损耗较大的问题,但该变换器对输出电压调节能力有限。文献[11-13]则对几种隔离型升压直流变换器拓扑进行了分析对比,并指出移相全桥变换器是比较优化的选择,但移相全桥变换器在轻载时很难实现软开关,同时高压大容量中高频变压器的设计与制造难度极大,目前尚无工业样机的报道。
英国阿伯丁大学的 D. Jovcic教授提出一种谐振升压变换器,可在全负载范围内实现开关器件的软开关以及避免二极管反向恢复损耗问题,并容易得到很高的电压增益,对5MW、4kV/80kV变换器进行了仿真分析,预估效率在95%左右[14]。中国电力科学研究院的温家良教授等也提出了类似的谐振升压变换器拓扑[15-17]。但该类谐振升压变换器也存在如下一些不足:①开关器件都需要具有反向电压阻断能力(如晶闸管),而为了提高开关频率,若使用IGBT,则需要在IGBT中串联二极管,带来了额外的导通损耗并增加了成本;②在整个负载范围内开关频率变化很大,不利于输入/输出滤波器的设计;③谐振电感单向磁化[14]或非对称双向磁化[15-17],磁心利用率不高,导致谐振电感体积和重量都较大,损耗也相应增加。
针对上述谐振变换器的不足,同时结合新能源并网对升压直流变换器的需求,本文提出了一种新型谐振升压变换器,该变换器可实现很高的电压增益,并可实现开关管的零电压开通和近似零电压关断以及整流二极管的零电流关断,同时开关频率变化范围小,谐振电感对称双向磁化。本文详细分析了所提出的谐振升压变换器的工作原理,并对谐振参数进行了优化设计,在实验室完成了一台 100V/ 1kV、1kW 的原理样机,验证了该变换器的工作原理,并给出了实验结果。
1 工作原理分析
图1为本文提出的谐振升压变换器主电路结构图,主要由输入阻断二极管VDi、全桥电路、LC并联谐振网络和输出整流电路组成。图2给出了该变换器的主要工作波形,Q2、Q3同时开通和关断,Q1、Q4同时开通和关断,一个开关周期包括 12个开关模态,其等效电路如图3所示。在分析之前,作如下假设:①所有开关管、二极管、电感和电容均为理想元器件;②输出滤波电容Co足够大,输出电压Vo为恒定电压。

图1 谐振升压变换器Fig.1 Resonant step-up converter

图2 主要工作波形Fig.2 Key waveforms
1.1开关模态1
模态1[t0, t1]:在t0时刻开通Q1和Q4,谐振电容Cr两端电压vCr=Vin,Vin加在谐振电感Lr两端,向Lr储能,iLr从I0线性增加,负载电流由Co提供,t1时刻iLr增加到I1,如图3a所示。

式中,T1为t0~t1的时间间隔。

图3 各种开关模态下的等效电路Fig.3 Equivalent circuits of each operation stage
Vin向Lr中存储的能量为

1.2开关模态2
模态2[t1, t4]:如图3b所示。在t1时刻关断Q1和 Q4,此后 Lr与 Cr发生并联谐振,即 Cr向 Lr放电,vCr从 Vin开始下降,iLr从 I1谐振增加,与此同时,A点电位vA从Vin开始下降,B点电位vB从零开始上升,由于开关器件的输出电容 Coss(在图中没有画出)相于对Cr很小,在Q1和Q4关断时间内,其两端电压(对IGBT而言,即集电极与发射极间电压)上升很小,可以近似看为零电压关断。
到t2时刻,vCr下降为零,iLr谐振增加到其最大值,vA=vB=Vin/2。此后 Lr对 Cr反向充电,vCr从零负向增加,iLr开始谐振下降,vA从Vin/2继续下降,vB从Vin/2继续上升。
到 t3时刻,vCr= −Vin,vA=0,vB=Vin。此时 Q2和 Q3两端电压均已下降到零,可以零电压开通 Q2和 Q3。此后 Lr继续对 Cr进行反向充电,vCr从−Vin继续负向增加,iLr继续谐振下降,此时输入阻断二极管 VDi将承受反向电压,vB从 Vin继续上升,直到t4时刻,vCr=−Vo,iLr下降到I2。
可见,在t1~t4这段时间内,只是Lr和Cr之间进行能量交换,但Lr和Cr上的总能量不变,即

利用拉普拉斯变换求得

式中,T2为t1~t4的时间间隔。
1.3开关模态3
模态3[t4, t5]:如图3c所示。在t4时刻,vCr=−Vo,VDR1和 VDR4自然导通,iLr流过 VDR1和 VDR4给Co充电,并提供负载电流,vCr保持不变,iLr线性下降,直到t5时刻,iLr=0,此开关模态结束。
t4~t5的时间间隔T3为

在此开关模态内Lr向负载端传递的能量为

负载在半个开关周期内消耗的能量为

式中,Ts为开关周期。
根据能量守衡定则,在半个周期内有

由式(7)~式(10)可得
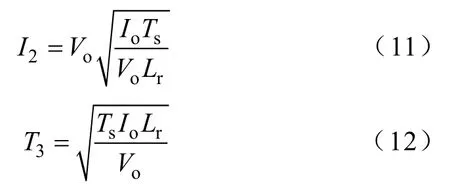
1.4开关模态4
模态 4[t5, t6]:如图 3d所示。在 t5时刻,iLr下降到零,VDR1和 VDR4自然关断,此后 Lr与 Cr发生并联谐振,即Cr向Lr放电,vCr从−Vo开始正向上升,iLr从零开始负向谐振增加,与此同时,B点电位vB开始下降。直到t6时刻,vCr= −Vin,iLr= −I3,此开关模态结束。在这段时间内,Lr和Cr上的总能量保持不变,即

可得

利用拉普拉斯变换可得

若在 t6时刻之前开通Q2和Q3,则在t6时刻之后,Q2和Q3自然导通,Vin通过Q2和Q3向Lr储能,iLr负向线性增加,其开关模态类似于开关模态1。
若在 t6时刻之前没有开通 Q2和Q3,则t6时刻之后,Lr与 Cr的并联谐振将使 vA从零开始谐振上升,vB从Vin开始谐振下降,此时若再开通Q2和Q3,则失去零电压开通条件,因此为减小开关损耗,Q2和Q3须于t6时刻之前开通。
2 变换器特性分析及参数设计
在半个周期内有

由式(1)、式(2)和式(14)可得

由式(19)可得

从式(20)可以看出,对于任何给定的Vin、Vo、Lr、Cr和 Io(其中 Vo>Vin),总可以找到一对 Ts和T1组合满足式(20),即说明该变换器谐振参数对电压增益没有影响,只要控制得当,变换器可工作在任意电压增益条件下。此外,对于给定的Vin、Vo和 Io,Lr与 Cr参数不同,则将有不同的 Ts和 T1组合满足式(20),说明该变换器谐振参数设计将影响到工作频率范围。
由式(1)、式(14)和式(20)可得

将式(21)代入式(3),可得

将式(21)代入式(6),可得

由式(12)、式(17)、式(18)、式(20)和式(23)可得

在空载情况下有Io=0,则由式(24)可得在空载情况下,有

式中,fs为开关频率;fr为Lr与Cr的谐振频率。
可见,在空载条件下,该变换器的开关频率等于Lr与Cr的谐振频率。其实从图2也可以直观地看出,在空载时,由于没有能量的输入(T1时段)与输出(T3时段),也即T1=T3=0,则变换器一直处于谐振状态,所以开关频率就等于谐振频率。而在有载情况下,T1,T3>0,则开关频率低于谐振频率,负载越重,开关频率越低。可见该变换器的最高开关频率为

从第1节分析可以看出,为了实现开关管的零电压开通,变换器的最小占空比为

而允许的最大导通时间为t3~t7时段,由式(5)可得t1~t3的时间间隔ΔT为

则变换器的最大占空比为

下面以一个具体例子来对该变换器参数进行设计,设Vin=100V,Vo=1kV,Iomax=1A,fsmax=10kHz。根据式(24)可求得满载时Ts关于Lr的表达式,但式(24)表明 Ts是与 Lr相关的隐函数,无法得到Ts的解析解。借助数学分析软件Maple进行数值计算,可以得到Lr与Ts的关系曲线,如图4所示。
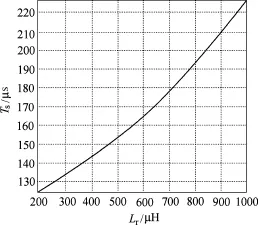
图4 Lr与Ts关系曲线Fig.4 The relationship curve between Lrand Ts
由式(14)可以得到Lr与Io的关系曲线,如图5中虚线所示,由于无法通过 Maple软件直接得到Lr与I1的关系曲线,只能通过式(21)和式(24)描点得到,如当 Lr=200μH时,通过式(24)可得Ts=125μs,再代入式(21)可得I1=91.46A。

图5 Lr与Io和I1关系曲线Fig.5 The relationship curves between Lrand I0, I1
从图4可以看出,Lr越小,满载时Ts越小,开关频率越高,即开关频率变化范围越窄,有利于输入、输出滤波器和磁性元件的设计;反之,Lr越大,满载时Ts越大,开关频率越低,即开关频率变化范围越宽,则不利于输入、输出滤波器和磁性元件的设计。而从图5可以看出,Lr越小,Io和 I1越大,即开关管和二极管的峰值电流越大,不利于开关器件的选择;而Lr越大则有利于开关器件选择。
可见,Lr的选择需要折中考虑以上两方面的影响,选定最高开关频率为10kHz,则选Lr=630μH,Cr=0.49μF,从图 4和图 5可得最低开关频率约为5.8kHz,开关管峰值电流约为35A。

图6 Dmin和Dmax曲线Fig.6 The curves of Dminand Dmax
Lr与Cr参数确定后,则由式(27)~式(29)可得在不同负载电流时的Dmin和Dmax曲线,如图6所示。从图中可见,Dmin和Dmax都随负载电流增大而增大,Dmin最大值为0.16,Dmax最小值约为0.47。因此,为了在整个负载电流范围内实现开关管的零电压开通,开关管占空比取在0.16~0.47区间内的任意值都可以,如图6的阴影区所示。
3 实验验证
为了验证所提出的谐振升压变换器的可行性,本文设计了一台最大负载1kW的原理样机。具体参数如下:输入直流电压 Vin=100V,输出电压Vo=1 000V,输出满载电流 Iomax=1A,最高开关频率 fsmax=10kHz,由于实际产品选型限制,选 Cr=0.5μF,Lr=630μH。1kW、500W以及20W负载情况的工作波形如图7所示。
从图7可以看出,实验结果和理论分析相一致,由图7b、图7d和图7f可以看出,IGBT开通时,其发射极和集电极之间电压已为零,当 IGBT关断时,发射极和集电极之间电压上升很小,可见其实现了零电压开通和关断;此外,整流二极管也实现了零电流关断。在1kW负载时变换器开关频率约为5.8kHz,在500W负载时变换器开关频率约为6.8kHz,在 20W负载时变换器开关频率约为 7.9kHz,与理论设计相吻合。


图7 谐振升压变换器实验波形Fig.7 Experimental results of the step-up resonant converter
4 结论
针对高压大功率升压变换应用场合,本文提出了一种可实现高电压增益的谐振变换器,详细分析了该谐振变换器的工作原理以及工作特性,并进行了详细的参数设计,最后通过一台100V/1kV、1kW原理样机进行了实验验证。该谐振变换器具有如下优点:①所有开关管在全负载范围内均实现了ZVS;②输出整流二极管实现了ZCS,且其电压应力为输出电压;③开关频率变化范围较小,易于优化设计磁性元件。
[1] 温家良, 吴锐, 彭畅, 等. 直流电网在中国的应用前景分析[J]. 中国电机工程学报, 2012, 32(13): 7-12. Wen Jialiang, Wu Rui, Peng Chang, et al. Analysis of DC grid prospects in China[J]. Proceedings of the CSEE, 2012, 32(13): 7-12.
[2] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12. Xu Dianguo, Liu Yuchao, Wu Jian. Rewiew on control strategies of multi-terminal direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 1-12.
[3] 陈霞, 林卫星, 孙海顺, 等. 基于多端直流输电的风电并网技术[J]. 电工技术学报, 2011, 26(7): 60-67. Chen Xia, Lin Weixing, Sun Haishun, et a1. LCCMTDC technology for wind farms integration[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 60-67.
[4] 李响, 韩民晓. 海上风电串联多端VSC-HVDC协调控制策略[J]. 电工技术学报, 2013, 28(5): 42-48. Li Xiang, Han Minxiao. A coordinated control strategy of series multi-terminal VSC-HVDC for offshore wind farm[J]. Transactions of China Electrotechnical Society, 2013, 28(5): 42-48.
[5] 汤广福, 罗湘, 魏晓光. 多端直流输电与直流电网技术[J]. 中国电机工程学报, 2013, 33(10): 8-17. Tang Guangfu, Luo Xiang, Wei Xiaoguang. Multiterminal HVDC and DC-grid technology[J]. Proceedings of the CSEE, 2013, 33(10): 8-17.
[6] Zhan C, Smith C, Crane A, et al. DC transmission and distribution system for a large offshore wind farm[C]// IET AC and DC Power Transmission, 2010: 1-5.
[7] Erickson R W, Maksimovic D. Fundamentals of power electronics[M]. MA: Kluwer Academic, 2001.
[8] Denniston N, Massoud A, Ahmed S, et al. Multiple module high gain high voltage DC-DC transformers for offshore wind energy systems[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1877-1886.
[9] Chen W, Huang A, Lukic S, et al. A comparison of medium voltage high power DC/DC converters with high step-up conversion ratio for offshore wind energy systems[C]//Proceedings of IEEE Energy Conversion Congress and Exposition (ECCE), 2011: 584-589.
[10] Chen W, Huang A, Li C, et al. Analysis and comparison of medium voltage high power DC/DC converters for offshore wind energy systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 2014-2023.
[11] Max L. Design and control of a DC collection grid for a wind farm[D]. Göteborg: Chalmers University of Technology, 2009.
[12] Zhou Y, Macpherson D E, Blewit W, et al. Comparison of DC-DC converter topologies for offshore wind-farm application[C]//Proceedings of IET Power Electronics, Machines and Drives (PEMD), Bristol, 2012: 1-6.
[13] Fan S, Ma W, Lim T C, et al. Design and control of a wind energy conversion system based on a resonant DC/DC converter[J]. IET Renewable Power Generation, 2011, 7(3): 265-274.
[14] Jovcic D. Step-up DC-DC converter for megawatt size applications[J]. IET Power Electronics, 2009, 2(6): 675-685.
[15] 温家良, 王秀环, 李跃, 等. 一种用于新能源并网的谐振升降压装置及其实现方法: 中国, 201210338755.3[P]. 2015.
[16] 温家良, 王秀环, 郭高鹏, 等. 一种用于新能源并网的谐振升压装置: 中国, 201210456865.X[P]. 2012.
[17] Jabbari M, Farzanehfard H, Farhangi S. A new resonant step-up converter based on unibirectional switches[C]//Proceedings of IEEE EuroCon, 2009: 849-852.
A Step-Up Resonant Converter for Grid-Connected Renewable Energy Sources
Due to soft-switching for switching devices, resonant converters are suitable for high-power applications. This paper proposes a resonant converter which is suitable for grid-connected renewable energy sources. The converter can achieve high voltage-gain using LC parallel resonant tank. It has the features such as zero-voltage-switching (ZVS) turn-on, nearly ZVS turn-off, and zero-currentswitching (ZCS) turn-off of rectifier diode. In addition, compared with the conventional resonant converter, the switching frequency variation of the proposed resonant converter is smaller over the entire load range. The operation principle of the converter and the selection of the resonant parameters are presented in the paper. A 1kW prototype is built in the lab to verify the effectiveness of the converter.
Resonant converter, voltage step-up, renewable energy source, soft switching
TM46
陈 武 男,1981年生,博士,副研究员,研究方向为功率电子变换技术及分布式发电技术。
E-mail: chenwu@seu.edu.cn(通信作者)
吴小刚 男,1990年生,硕士研究生,研究方向为功率电子变换技术。
E-mail: 404377617@qq.com
国家自然科学基金(51307024),教育部博士点基金(20120092120053),中央高校基本科研业务费专项资金(2242014R30018),教育部留学回国人员科研启动基金和国家电网公司专项支持项目(国家电网科研(2013)304号)资助。
2014-04-08 改稿日期 2015-05-27

