利用半波傅里叶算法的两面积法识别励磁涌流

张冬林，夏宇杰，高仕斌，韩正庆

（1.西南交通大学电气工程学院，成都　610031；2.福建省电力勘测设计院，福州　350003）

利用半波傅里叶算法的两面积法识别励磁涌流

张冬林1，2，夏宇杰1，高仕斌1，韩正庆1

（1.西南交通大学电气工程学院，成都610031；2.福建省电力勘测设计院，福州350003）

为了识别变压器励磁涌流和内部故障电流，通过分析由半波傅里叶算法计算差动电流的基波幅值的变化特征，提出了一种基于半波傅里叶算法得到的基波幅值的波动系数的判据方法。该方法先对差动电流进行一阶差分滤波处理，用半波傅里叶算法求得基波幅值，选取工频一周波内计算所得基波幅值为数据窗，将其分成两段后各自求得面积，通过求得小面积与大面积比的最小值来识别励磁涌流和故障电流，该方法具有抗CT稳态饱和特性。通过理论分析和大量动模实验验证了该方法的准确性和可靠性。

励磁涌流；故障电流；波动系数；半波傅里叶算法；稳态饱和

电力变压器是电力系统的重要设备之一，其安全可靠运行是至关重要的。但是根据资料显示，在2001—2005年间，220 kV及以上等级变压器的平均正确动作率为79.794%，远低于发电机及线路保护的98.1%及99.622%[1]，造成这一局面的关键问题在于如何准确地识别励磁涌流和内部故障电流。

文献[2]提出基于半波傅里叶算法的励磁涌流识别方法，近年来许多学者基于半波傅里叶算法提出了许多励磁涌流识别的方法，主要分两种，一种是基于不同傅里叶算法引入了波形相似度系数和波形相关性等识别方法[3-5]；另一种是基于波形特征识别方法，如波动误差[6]、波形正弦特性[7-9]、利用波形曲率[10]、以及改进的滤波识别法[11]。

本文利用半波傅里叶算法计算得到基波幅值波形，分析其特征提出一种基于基波幅值波动特性的励磁涌流识别新方法。该方法通过选取基波幅值的一工频周波数据窗，分成两部分后求得小面积和大面积比的最小值来识别励磁涌流和故障电流。该方法受非周期分量和高频分量的影响很小，计算量小，稳定可靠，易实现。通过理论分析，得出该方法可以有效抗CT（电流互感器）稳态饱和。理论分析和大量的动模试验结果表明，该方法能够可靠、快速地区分励磁涌流和内部故障电流。

1　半波傅里叶算法分析

假定输入为正弦电流可表示为

对电流i(t)采用半波傅里叶算法分别计算其正弦分量和余弦分量，结果为

式中：I1s为基波的正弦分量；I1c为余弦分量（下同）。

式中：N为每个工频周期的采样点数；k和ik分别为第k次采样及其采样值。

大量的工程实践表明励磁涌流具有尖顶波特性，且还含有间断角。经分析其内部含有较高的直流分量和谐波分量，尤其以偶次谐波居多，并且包含许多非周期分量。为了消除非周期分量影响，文中在用半波傅里叶算法求基波幅值之前，先对差流进行一阶差分滤波处理[4]。

图1（a）为变压器发生励磁涌流时的差流波形，对其采用半波傅里叶算法计算基波幅值得到如图1（b）所示。从图中可以看到，基波幅值跟随励磁涌流的发生周期性变化，剧烈波动。其主要原因是励磁涌流波形存在间断角。

图1　励磁涌流分析Fig.1　Analysis of magnetizing inrush currents

图2（a）是变压器发生内部故障时的差流波形，同样对其采用半波傅里叶算法计算基波幅值得到如图2（b）所示。从图中可以看出此时基波幅值虽同样随故障差流发生周期变化，但波动不大。图2的仿真结果与理论分析基本相符。

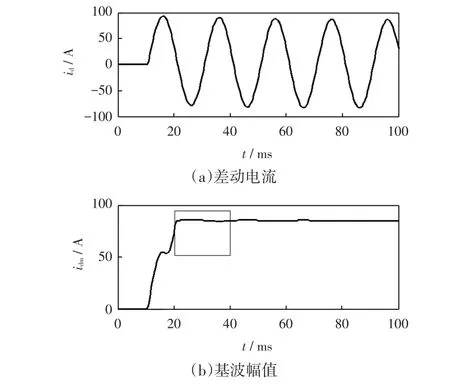
图2　内部故障电流分析Fig.2　Analysis of inside fault currents

2　励磁涌流判据及实现

设变压器的差动电流采用值用id(t)表示，采用半波傅里叶算法得到的基波幅值为Idm(k)，在基波幅值中选取一个长度为一个周期的观察窗，长度为N。如图2（b）所示，以观测窗左侧围参考时刻。

为了下面定义基波幅值的波动系数，令

设Smax为S(k)的最大值，为了求取Smax，必须要考察0≤k≤N-1范围内S(k)所有值，比较得出最大值Smax。即

由于对变压器空载合闸时产生的励磁涌流采用半波傅里叶算法计算得到的基波幅值如图1（b）所示，空载合闸后基波幅值随励磁涌流发生周期性上下剧烈波动，因此Smax要比Smin大得多。而对变压器内部故障时的差动电流采用半波傅里叶算法计算得到的基波幅值如图2（b）所示，故障发生后基波幅值波动很小，因此对其选取的任意一个观测窗内Smax与Smin基本相等。因此本文以此来区分励磁涌流和内部故障电流，定义波形系数为

式中，σ称为波形波动系数。

σ即为两个面积的比值。假设变压器处于某种运行状态（比如内部故障），保护装置对差动电流进行实时采样得到采样数据，在采样数据中选取观测窗进行σ的计算，并对数据窗内的数据进行定时地更新（数据更新的数量根据采样频率而定），从而不断得到最新的σ。

因此本文鉴别励磁涌流和内部故障的判据如下，即

式中，σdz为整定值

文中σ与常规的二次谐波制动相类似，从式（6）和（8）可以知道，为了尽可能精确地计算出Smax和Sum，对于采样频率有一定的要求，但是由于其计算中基本只做加法，因此其所需的计算时间很短，缩减了保护动作时间。

3　模拟试验

为了验证上述方法的可行性，本文进行了大量的模拟试验进行验证。模拟试验中，利用3个单项变压器，采用Yn/d11的接线，单个变压器参数如下：10 kVA，高压侧额定电压为1 kV，低压侧额定电压为400 V，模拟试验的数据采样频率为5 kHz，模拟了多种工况：空载合闸、高压侧单相接地及相间短路故障、低压侧相间短路故障、高压侧单相2.76%及6.54%匝间短路故障、带内部故障的空载合闸等。对大量工况下的模拟试验进行了仿真计算，在考虑一定裕度的情况下，波动系数整定值σdz取0.8能够可靠的识别励磁涌流和内部故障。

对三相差流idAB、idBC、idCA进行计算得到的σ分别用σAB、σBC、σCA来表示，下面是几种工况（CT不饱和）下的仿真计算及分析结果。

3.1空载合闸

变压器组空载合闸产生励磁涌流，动模试验结果如图3所示。

图3（a）中，变压器三相差流idAB、idBC、idCA中产生了幅值接近3倍额定电流的励磁涌流。图3（b）可见三相差流经半波傅里叶算法得到的基波幅值的波动系数所反映的信息几乎是相同的，均能正确各项发生励磁涌流现象，σ值均小于整定值σdz，变压器能够可靠闭锁。

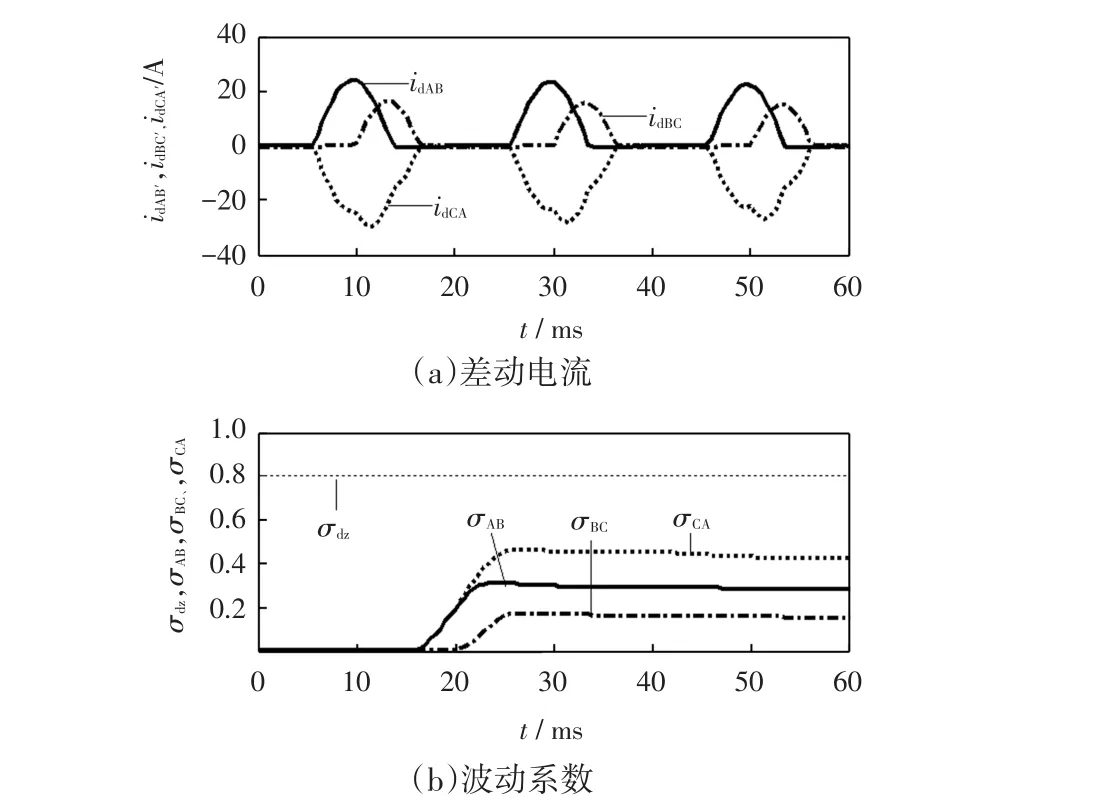
图3　空载合闸Fig.3　Switch closing on a no-load transformer

3.2内部故障

变压器处在正常运行的情况下，高压侧A相发生2.76%的匝间短路故障，试验结果见图4。

图4　内部故障Fig.4　Phase-to-ground inside fault

由于变压器采用的是Yn/d11的接线方式，所以高压侧的电流互感器二次侧采用三角形接线，差动电流是两相电流的差值。当高压侧A相绕组发生故障时，将反映到差流idAB和idCA上。从图4（b）可以看出，波动系数σAB和σCA基本重合，都能够可靠的识别内部故障，保护开放并动作于跳闸。差流idBC和变压器正常运行时的差流波形相似，因此保护不动作。

3.3带内部故障空载合闸

变压器带内部故障进行空载合闸时，由于待合闸电压相位的不同，故障电流和励磁涌流可能同时存在，非故障相亦有可能产生励磁涌流。图5为变压器高压侧A相发生2.76%的匝间短路故障时的空载合闸仿真波形。

由图5（a）与图4（a）比较得出，变压器空投于内部故障时，差流idAB和idCA受到励磁涌流的影响发生畸变。图5（b）中可以看出，波动系数σAB和σCA仍可以可靠地识别内部故障，保护快速开放并动作于跳闸。而此时差流idBC则是变压器正常运行情况下的励磁涌流，所以差动保护不会动作。由图3～图5可以看出变压器带内部故障空载合闸时，保护启动到保护出口所需最长时间为一周期20 ms，其满足变压器对于差动保护的动作要求。

图5　带内部故障空载合闸Fig.5　Switch closing with inside fault

随着变压器容量的急剧增加，空载合闸或出现短路故障产生的大电流可能引起CT饱和，包括CT稳态饱和及CT暂态饱和，导致二次输出值发生畸变。文献[13]中通过运行试验表明，95%的CT饱和为CT稳态饱和，CT稳态饱和引起的畸变不改变正弦信号绝对值的半波周期性（正弦信号绝对值的周期减半），因此文中提出的方法可以有效抗CT稳态饱和。

变压器的差动保护分相制动逻辑如图6所示，由图3、图4可以知道，该方案可以保证差动保护正确动作。

图6　差动保护制动逻辑Fig.6　Braking of logic differential protection

4　结语

本文通过分析半波傅里叶算法计算得到的基波幅值的特征，引入非参数系数，提出了一种基于傅氏算法计算得到基波幅值的波动系数来识别励磁涌流和内部故障电流，通过大量的动模试验可知，对差流采用半波傅里叶算法计算基波幅值，发现励磁涌流下的基波幅值波动剧烈，内部故障下的基波波动很小，本文以此为出发点提出了一种基于基波幅值波动系数的励磁涌流识别方法。通过理论分析和动模试验，验证了该方法能够可靠、快速地识别励磁涌流和内部故障电流。

[1]沈晓凡，程逍，章激扬（Shen Xiaofan，Cheng Xiao，Zhang Jiyang）.2005年全国电网继电保护装置运行情况分析（Operation condition and analysis of protective relaying in 2005）[J].电力设备（Electrical Equipment），2007，8（2）：26-29.

[2]韩正庆，高仕斌，李群湛（Han Zhengqing，Gao Shibin，Li Qunzhan）.基于半波傅里叶算法的励磁涌流识别方法（New method to identify inrush current based on halfwave Fourier analysis）[J].电力系统自动化（Automation of Electric Power Systems），2005，29（14）：60-63.

[3] 陈达壮，黄家栋，张玲（Chen Dazhuang，Huang Jiadong，Zhang Ling）.基于2种傅氏算法相关性分析的变压器励磁涌流识别方法（Identification of transformer excita⁃tion inrush based on correlation analysis between two Fourier algorithms）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（10）：71-74.

[4]陈俊，严伟，陈佳胜，等（Chen Jun，Yan Wei，Chen Jiash⁃eng，et al）.基于不同傅里叶算法之间相似度的励磁涌流鉴别方法（Novel identification method for magnetiz⁃ing inrush current based on the comparability of different Fourier algorithm）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（6）：21-24.

[5]韩正庆，刘淑萍（Han Zhengqing，Liu Shuping）.一种基于差动电流波形特征的励磁涌流识别新方法（Magne⁃tizing inrush identification based on differential current characteristics）[J].电力自动化设备（Electric Power Au⁃tomation Equipment），2007，27（9）：51-54.

[6]尤夏，张艳霞（You Xia，Zhang Yanxia）.波动误差结合峰-峰间距法识别变压器励磁涌流（Recognition of transformer inrush current based on combination of fluc⁃tuation error and peak-to-peak space method）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（14）：36-40，45.

[7]陈达壮，张玲（Chen Dazhuang，Zhang Ling）.半波傅氏算法与两点乘积算法相结合的励磁涌流识别新方法（New algorithm to identify inrush current based on halfwave Fourier and two points product method）[J].电力系统保护与控制（Power System Protection and Control），2010，38（17）：138-141.

[8]文超，黄纯，胡鹏，等（Wen Chao，Huang Chun，Hu Peng，et al）.利用波形非正弦度分形估计值识别励磁涌流（Identification of transformer inrush current by us⁃ing of fractal evaluation of waveform non-sinusoidal lev⁃el）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（4）：71-76.

[9]姚斌，李永丽（Yao Bin，Li Yongli）.基于波形上下对称系数识别励磁涌流的新原理（Novel theory of identify⁃ing inrush current based on waveform longitudinal sym⁃metry）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2004，16（2）：32-35.

[10]李波，江亚群，候立峰，等（Li Bo，Jiang Yaqun，Hou Li⁃feng，et al）.利用波形曲率识别变压器励磁涌流的新方法（Novel method to identify transformer inrush cur⁃rent based on the curvature characteristics of waveform）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2010，22（6）：93-98.

[11]李斌，李永丽，贺家李（Li Bin，Li Yongli，He Jiali）.一种提取基波分量的高精度快速滤波算法（Accurate and fast filtering algorithm for fundamental component）[J].电力系统自动化（Automation of Electric Power Systems），2006，30（10）：39-43，74.

[12]贺威俊，张淑琴，王建平，等.晶体管与计算机继电保护原理[M].成都：西南交通大学出版社，1990.

[13]韩正庆（Han Zhengqing）.变压器仿真计算模型与保护原理研究（Study on Simulation Model and Protective Schemes for Transformer）[D].成都：西南交通大学电气工程学院（Chengdu：School of Electrical Engineering，Southwest Jiaotong University），2006.

Two Area of Identification of Excitation Inrush Current by Using the Half-wave Fourier Algorithm

ZHANG Donglin，XIA Yujie，GAO Shibin，HAN Zhengqing
（1.School of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China；
2.Fujian Electric Power Surrey&Design Instttute，Fuzhou 350003，China）

In order to identify transformer excitation inrush current and internal fault current，by analyzing the charac⁃teristics of fundamental current amplitude calculated by half-wave Fourier algorithm，hence this paper presents a meth⁃od based on the fluctuation coefficient of fundamental current amplitude calculated by half-wave Fourier algorithm.The method samples currents with differential filter continuously，obtains the fundamental current amplitude based halfwave Fourier，selects the data of power frequency as the data window，acquires the respective area after dividing into two，and obtains the ratio of small area and big are to identify magnetizing inrush from inside fault current.The method has good resisting current transformer（CT）steady saturated features.Theoretical analysis and dynamic simulation re⁃sults show that the method is correct and effective under various fault conditions.

magnetizing inrush current；fault current；fluctuation coefficient；half-wave Fourier algorithm；steady sat⁃uration

TM772

A

1003-8930（2016）02-0069-04

10.3969/j.issn.1003-8930.2016.02.011

张冬林（1989—），男，硕士研究生，研究方向为继电保护与变电站综合自动化。Email：zhangdonglin1946@163.com

夏宇杰（1987—），男，硕士研究生，研究方向为继电保护与变电站综合自动化。Email：867769603@qq.com

高仕斌（1963—），男，博士，教授，研究方向为继电保护与变电站综合自动化。Email：gao_shi_bin@126.com

2014-02-25；

2015-05-13

国家自然科学基金重点项目（U1134205）