考虑节点补偿容量上限的弱环配网无功优化
胡晓阳,王主丁,边昱鹏
(1.输配电装备及系统安全与新技术国家重点实验室,重庆大学电气工程学院,重庆 400044;2.云南省电网公司曲靖供电局,曲靖 655000)
考虑节点补偿容量上限的弱环配网无功优化
胡晓阳1,王主丁1,边昱鹏2
(1.输配电装备及系统安全与新技术国家重点实验室,重庆大学电气工程学院,重庆400044;2.云南省电网公司曲靖供电局,曲靖655000)
为了合理确定节点无功补偿的位置和容量上限,基于遗传算法和弱环状配网特点,通过引入无功补偿分布因子来处理环网,提出一种可动态确定含弱环配网的节点补偿容量上限算法。综合考虑补偿效益和节点电压约束,通过计算补偿净效益最大、节点电压约束两种情况下的节点无功补偿容量上限,有效压缩了遗传算法的寻优空间。通过对IEEE33节点系统算例的分析,验证了算法在含弱环配网无功优化中的实用性。
无功优化;遗传算法;弱环配网;无功补偿分布因子;节点补偿容量上限
配电网无功优化是保证系统安全、经济运行的一种有效手段,是提高电力系统电压质量、降低电能损耗的重要措施。配电网一般呈辐射状结构运行,但在线路检修、负荷转移等实际运行情况下,部分联络线支路的闭合形成了环网[1-2]。随着电力系统的不断发展,电能生产的激增[3],电网结构日益复杂,配网中也可能出现多个环网,因此有必要对含环网的配网进行无功优化研究。
对于辐射状的配网无功优化,国内外学者已做了很多研究。文献[4]以无功补偿设备投资和系统有功网损的综合费用为目标函数,同时考虑电压水平和电压稳定性两个约束条件建立无功规划模型,采用非线性原对偶内点法来求解。但其是在无功补偿点候选位置已给定的情况下计算无功补偿设备的最佳安装容量,没能说明如何确定无功补偿节点的候选位置。文献[5-7]采用灵敏度分析方法,选择少数高灵敏度节点作为候选补偿点,但难以确定具体补偿的节点,且所选补偿节点常常集中在负荷较重区域的几个点,容易导致补偿范围的重叠,造成无功浪费。文献[8-9]选择系统的电压稳定性较弱的节点作为无功补偿装置的最佳配置地点,但不能保证补偿点的最优性。文献[10]使用模态分析技术,找出电压易于失稳区域的节点作为无功补偿节点,但有些节点电压稳定仍需补偿,这容易错漏补偿点,导致搜索范围的不全面。文献[11]提出利用节点无功裕度的排序确定电力系统无功补偿点,但难以确定补偿点的具体个数。文献[12]以有功网损最小为目标函数,结合最优网损微增率准则和层次聚类法确定待补偿点范围,采用蚁群算法确定无功补偿最佳补偿位置和容量。
文献[13-14]可动态确定补偿节点总数及节点补偿容量上限,但是不能很好地处理含环网的配网。对于辐射状配网,如果在网络中某个节点进行无功补偿,该节点上游支路上无功功率会变化,而其他支路的无功功率基本不变[15]。当配网含有环网时,无功功率的分布将发生变化,目前的方法在处理含环网配网无功优化时就出现很大的困难。
针对含弱环的配电网,本文引入无功补偿分布因子,确定节点补偿无功时环网支路的无功分布,并提出了一种适用于环网、可动态确定节点补偿容量上限的算法,较好地解决了弱环状配网的无功优化问题。算例验证了算法在无功优化中的实用性。
1 优化模型
1.1无功规划优化模型
1.1.1目标函数
以无功补偿后净节约最大为目标函数,即

式中:C1为配网无功补偿后的净收益值,万元/a;Ce为电能损耗边际值,万元/kWh;ΔPl1、ΔPl2分别为无功补偿前、后系统的最大有功功率损耗,kW;α、β分别为折旧维修率和投资回收率;M为所有补偿节点的集合;Ci v为节点i处补偿电容器的单位容量价格,万元/kvar;Qic为节点i处电容器的总补偿容量;Ci f为节点i补偿电容器的固定投资费用;若此节点为新增补偿点,系数a=1,否则a=0;τmax为最大负荷损耗小时数;ΔUi为节点i的电压越界值;Ui max、Ui min分别为节点i电压允许的上、下限;w为惩罚因子。
1.1.2约束条件
约束条件包括各节点的有功、无功功率平衡方程和各节点电压上下限。

1.1.3适应度函数
适应度函数由目标函数转化而来,要使目标函数值越大,则有
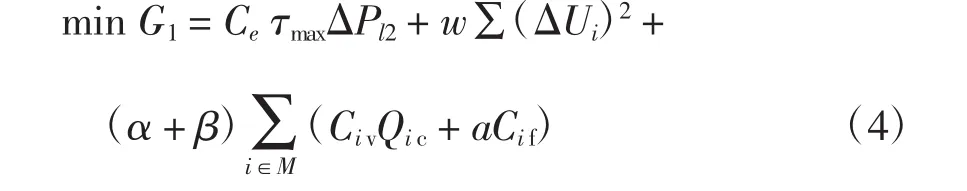
适应度函数f1取为式(4)的倒数,即

1.2无功运行优化模型
1.2.1目标函数

式中,ΔP为配网无功补偿后考虑了电压越限惩项的有功损耗减小值,kW。
1.2.2约束条件
除了需满足各节点的有功、无功功率平衡方程和各节点电压上下限约束条件外,还需满足
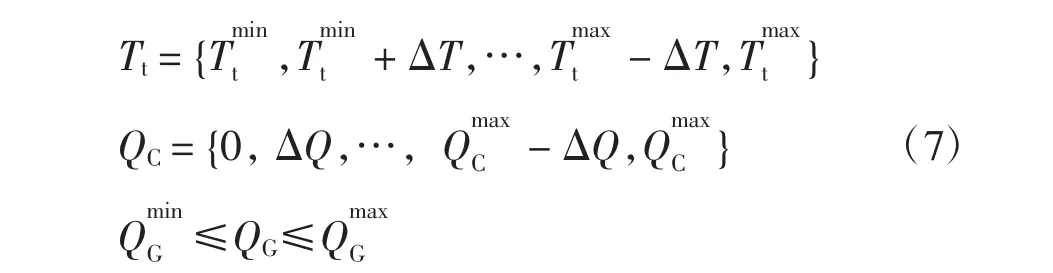
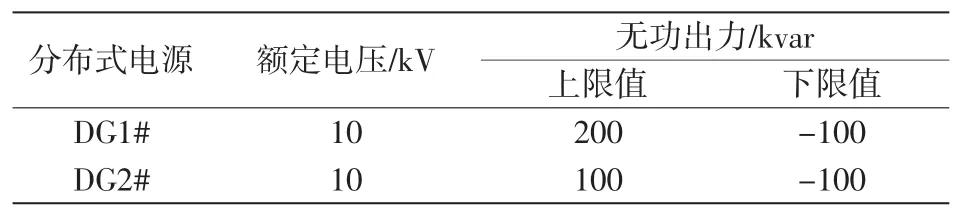
式中:变压器分接头Tt和无功电容器Qc为离散变量;分别为变压器的总档位数和无功电容器的总补偿组数;分布式电源无功出力QG为连续变量,分别为无功出力上、下限值。
1.2.3适应度函数
目标函数值越大,则有

适应度函数f2取式(8)的倒数,即

2 节点编号优化方法及环网支路识别
2.1节点编号优化方法
为了描述网络中各节点和支路的联结关系,需要对网络的节点和支路进行编号,本文采用的节点编号方法[16]只要求任意节点的新编号都要大于其上游父节点(即根节点方向)编号。
具体步骤是:首先,对网络中各支路两端节点任意编号(旧编号);其次,指定根节点(如上级电网源节点),将其编号为0;然后逐条支路搜索对所有节点重新编号。当搜索到某条支路时,会遇到以下3种情况:
情况1支路两端节点都未重新编号;
情况2支路两端节点仅有一个完成重新编号;
情况3支路两端节点都完成了重新编号。
在情况1下,跳过此支路,继续搜索下一支路;在情况2下,将未重新编号的节点进行重新编号,新编号为已经完成重新编号的节点总数;在情况3下,表明此支路是连支,网络中存在环网。当所有节点都完成重新编号后,支路搜索停止。
2.2环网支路识别
应用上节介绍的节点编号方法对节点编号之后,若存在连支,还需识别出环网各支路。对于每个连支,其独立回路识别步骤如下:
步骤1识别连支的两个端节点编号m3和m4;
步骤2若m3>m4,由m3搜索到其父节点m1,让m3=m1并重复该步骤;
步骤3若m3 步骤4若m3=m4,则停止搜索。 针对目前方法在处理含环网配网无功优化出现的困难,本文引入无功分布因子处理环网,确定环网各支路的无功功率分布。 3.1无功补偿分布因子 3.1.1环网节点无功补偿分布因子 1)单环情况 根据基尔霍夫定律,流过并联支路的无功电流与其阻抗成反比,若电压偏移不大流过并联支路的无功近似与其阻抗成反比。令Zik为节点某环网节点i到源节点的不经过支路k的阻抗,Z∑为环网支路总阻抗,无功补偿分布因子可表示为 2)多环情况 当配网中出现多个环网时,用阻抗比例关系难于表示分布因子。此时,可通过潮流计算,试探性地在节点i补偿单组标准电容器,通过计算补偿前后的潮流确定环网支路无功分布因子为 式中,Qk和Qik分别为补偿点i补偿单组标准电容器Qkc前后支路k的无功。 若一系统有N+1节点,0为源节点,无功分布因子计算流程如图1所示。 图1 无功分布因子计算流程Fig.1 Flow chart of computing reactive power distribution factors 3.1.2含环网的配网节点无功补偿分布因子 含环网的配网节点无功补偿分布因子计算分为以下几种情况: (1)若支路k位于环内,节点i为环网节点,按式(10)或式(11)求λik; (2)若支路k位于环内,节点i为环外节点但存在其上游环节点,若节点i上游的第1个环节点j,对于环内各支路,其补偿效果等同于在此环节点j补偿,此时λik=λjk,即可由式(10)或式(11)求λik; (3)若支路k和节点i均位于环外,且支路k位于节点i的上游,即为辐射状网络补偿情况,λik=1。 3.2含弱环配网无功优化补偿容量上限 现有遗传算法用于无功优化时,一般人为地指定补偿节点个数和补偿组数的上限,使得初始种群包含很多的无效解。本文通过综合考虑补偿经济效益和电压约束,动态确定节点的补偿组数上限,每个补偿节点的组数在0和最大补偿组数之间产生,使得初始种群包含尽可能多的可行解,有效压缩了遗传算法的寻优空间。 3.2.1无功规划优化 1)候选补偿点的最大补偿容量 单独在节点i进行电容器无功补偿时,所带来的含弱环配网降损效益Ai可近似表示为 式中:H为节点i所有上游支路的集合(包括环内各支路);Rk为支路k的电阻;Uk为支路k的末端节点的电压。 Ai对Qic求导,并令A′i=0得到的最大补偿容量为 式中,A=Ceτmax/U2k。 2)考虑节点电压约束的最小补偿容量 假设仅在含弱环配网节点i进行电容器无功补偿,该点电压损耗可近似表示为 由于配电网中节点电压不能低于其规定下限值,即ΔUi≤ΔUmax,可得 此时,补偿电容器组数上限mmax为 式中,Qicmax=max{Q*ic,Q**ic}。 3.2.2无功运行优化 1)候选补偿点的最大补偿容量 单独在节点i进行无功补偿时,所带来的含弱环配网降损效益Ai可近似表示为 式中,Qi表示节点i处的无功补偿容量,由电容器装置或分布式电源提供,当为分布式电源时,其值可正亦可负。Ai对Qi求导,求得并令A′i=0得到的最大补偿容量为 2)考虑节点电压约束的最小补偿容量 当单独在节点i补偿无功容量为Qi时,节点的电压可近似表示为 式中:U(i0)为节点i无功补偿前的电压;M为节点i所有下游支路端节点的集合;Qj为下游支路端节点j无功补偿容量;Xk为支路k的电抗。 当考虑变压器分接头对各节点电压的影响时,式(19)可进一步表达为 式中:k1=U1/U1B;k2=U2/U2(B上标“0”表示节点i无功Qic补偿前的值);U1、U2分别为高压变电站主变一次侧和二次侧绕组实际匝数相对应的电压;U1B、U2B分别为主变一次侧和二次侧相连网络的基准电压。U′i为当Qi为零时节点i无功补偿前的电压。 分别对U′i,低于规定下限值、U′i高于规定上限值和介于两者之间3种不同情况进行节点无功补偿容量上限或下限的计算: (1)当U′i<Uimin时,由于配电网中各节点的电压值不能低于规定的下限值Ui min,即Ui≥Ui min,由式(20)得节点i满足电压要求所需的最小补偿容量为 (2)当U′i>Uimax时,由于各节点的电压值不能高于规定的上限值Ui max,即Ui (3)当Ui min<Ui<Ui max时,节点i的电压满足要求,有 分别取由式(18)和式(21)计算得到较大值;由式(18)和式(22)计算得到较小值;由式(18)和式(23)计算得到的较大值作为节点i的最大补偿容量Ui max;若节点i处为电容器,仍由式(16)求得组数上限。 3.3初始解的生成 3.3.1无功规划优化初始解的生成 按优化节点编号从大到小进行补偿,无功规划优化初始解生成流程如图2所示。 图2 规划优化初始解生成流程Fig.2 Flow chart of generating initial solutions for optimal capacitor placement 3.3.2无功运行优化初始解的生成 无功运行优化初始解的生成同无功规划优化基本相同,其不同处在于: (1)原始参数包含随机产生的主变档位;(2)最大补偿容量Qimax的确定。 3.4算法流程 用本文方法形成初始种群后,将形成的初始种群用于遗传操作,求得各解的适应度值,采用文献[13]的收敛判据进行收敛,输出最优解。算法总流程如图3所示。 图3 算法总流程Fig.3 Flow chart of overall optimization algorithm 4.1无功规划优化算例 本文采用IEEE33节点网络进行算法的仿真测试,如图4所示。参数选取如下:Ce=0.45元/ kWh;Ckv=50元/kvar;Ckf=5 000元,τmax=5 000 h。α、β均取50%。电容器单组容量取为100 kvar,负荷采用恒功率模型。分别计算在节点7和节点20之间设置联络线,形成单环;在节点7和节点20之间,节点24和节点28之间设置联络线,形成双环两种情况。计算结果如表1和表2所示。单环和双环情况下,优化前后电压如图5和图6所示。 图4 IEEE33节点网络Fig.4 IEEE 33 node network 表1 补偿点的补偿容量和投资费用Tab.1 Capacitor sizes and investment costs for different locations 由表2和图5、图6可知,用本文方法补偿效益明显,一年就可以将投资费用收回,不仅降低了有功损耗,电压质量也得到改善,优化前个别节点低于9.3 kV,优化后节点电压都在9.5 kV以上。 表2 补偿效果比较Tab.2 Comparison on capacitor placement effects 图5 单环优化前后节点电压质量对比Fig.5 Comparison of voltages before and after the optimization with one mesh 图6 双环优化前后节点电压质量对比Fig.6 Comparison of voltages before and after the optimization with two meshes 4.2无功运行优化算例 在IEEE33节点系统基础上新增有载调压变压器一台,SN=31.5 MVA,110±8×1.25%/10.5。在节点12和节点32处各有1座小型水电站,编号分别为DG1#、DG2#,该类型DG既可提供无功,又可吸收无功。考虑单环情况验证本方法同样适用于运行优化,分布式电源和电容器参数设置、优化前后的主变分接头位置和电容器补偿情况见表3、表4和表5。优化前后的网损和电压质量比较见表6和图7。 由表6和图7知,优化后有功网损较优化前有了大幅下降,电压质量也得到很大的改善,优化前近一半节点电压低于9.3 kV,优化后电压质量得到明显改善,各节点电压均满足要求。 此外,采用文[13]计算无功规划优化算例,文[14]计算无功运行优化算例,均不能有效收敛。究其原因,当网络含有环网时,文献[13-14]不能准确的计算出环网各支路的无功功率分布,无法确定节点的最大补偿容量,进而影响了初始种群的生成,使得初始种群包含了很多无效解,不仅增加了搜索时间,还不能有效收敛。结合上述两个算例,本文所述方法在处理含环网配网时具有很大的优势,能有效生成初始种群,压缩搜索空间,减少了计算时间。 表3 IEEE33节点网络中分布式电源参数设置Tab.3 Parameters of distributed generations of IEEE33 node network 表4 IEEE33节点网络中无功补偿电容器参数设置Tab.4 Parameters of capacitors of IEEE33 node network 表5 IEEE33网络无功优化前后的设备状态对比Tab.5 A comparison of device status before and after the reactive power optimization 表6 IEEE33节点网络无功优化前后的网损对比Tab.6 A comparison of real power losses before and after the reactive power optimization 图7 优化前后节点电压质量对比Fig.7 Comparison of voltages before and after the optimization (1)本文通过引入无功分布因子,提出一种能处理含环网的配网无功优化方法,可动态确定各节点无功补偿组数的上限,综合考虑了补偿经济效益和电压约束,合理压缩了解空间,提高了寻优速度和质量。 (2)本文提出的方法应用于环网无功运行优化时综合考虑了有载调压变压器分接头、并联电容器和分布式电源,对含分布式电源的配网无功优化有一定的参考价值。 (3)一般配电架空线路的充电功率很小,本文只考虑容性无功补偿,如何考虑感性无功补偿是今后需要研究的问题。 [1]车仁飞,李仁俊(Che Renfei,Li Renjun).一种少环配电网三相潮流计算新方法(A new three-phase power flow method for weakly meshed distribution systems)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(1):74-79. [2]陈根军,王磊,唐国庆(ChenGenjun,WangLei,Tang Guoqing).一种求解环状配电网潮流的有效算法-两阶段法(An efficient two-stage load flow method for meshed distribution networks)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2001,13(5):5-9,14. [3]张程,王主丁,张宗益,等(Zhang Cheng,Wang Zhuding,Zhang Zongyi,et al).一种规划态配网无功补偿估算方法(A method for estimating reactive power compensation of distribution network planning)[J].电力建设(Electric Power Construction),2010,31(11):24-27. [4]刘明波,杨勇(Liu Mingbo,Yang Yong).计及静态电压稳定约束的无功优化规划(Optimal reactive power planning incorporating steady state voltage stability constraints)[J].电力系统自动化(Automation of Electric Power Systems),2005,29(5):21-25. [5]余健明,杜刚,姚李孝(YuJianming,DuGang,YaoLixiao).结合灵敏度分析的遗传算法应用于配电网无功补偿优化规划(Application of genetic algorithm combining sensitivity analysis to optimized planning of reactive power compensation for distribution networks)[J].电网技术(Power System Technology),2002,26(7):46-49. [6]Miu K N,Chiang H-D,Darling G.Capacitor placement,replacement and control in large-scale distribution systems by a GA-based two-stage algorithm[J].IEEE Trans on Power Systems,1997,12(3):1160-1166. [7]Sundhararajan S,Pahwa A.Optimal selection of capacitors for radial distribution systems using a genetic algorithm[J].IEEE Trans on Power Systems,1994,9(3):1499-1507. [8]李宏仲,金义雄,程浩忠,等(Li Hongzhong,Jin Yixiong,Cheng Haozhong,et al).基于改进粒子群优化算法并计及静态电压稳定性的电力系统无功规划(Reactive power planning based on improved panicle swarm optimization with static voltage stability)[J].电网技术(Power System Technology),2005,29(22):50-55. [9] 王东,魏庆海,孙辉,等(Wang Dong,Wei Qinghai,Sun Hui,et al).基于过渡状态的无功补偿装置的最优配置(Optimalallocation of reactive power compensating devices based on power system transition states)[J].电网技术(Power System Technology),2005,29(21):41-45. [10]蒋志平,唐国庆(Jiang Zhiping,Tang Guoqing).电力系统无功规划优化的变尺度混沌优化算法(Mutative scale chaos optimization algorithm for VAR planning of power system)[J].继电器(Relay),2007,35(2):33-39. [11]刘传铨,张焰(Liu Chuanquan,Zhang Yan).电力系统无功补偿点及其补偿容量的确定(Confirmation of reactive power compensation node and its optimal compensation capacity)[J].电网技术(Power System Technology),2007,31(12):78-81. [12]王韶,周鑫(Wang Shao,Zhou Xin).应用层次聚类法和蚁群算法的配电网无功优化(Optimization of reactive power in distribution network with hierarchical clustering and ant colony algorithm)[J].电网技术(Power System Technology),2011,35(8):161-167. [13]赵俊光,王主丁,张宗益,等(Zhao Junguang,Wang Zhuding,Zhang Zongyi,et al).基于节点补偿容量动态上限的配电网无功规划优化混合算法(A dynamic upper limit to node compensation based hybrid optimization algorithm for reactive power planning in distribution networks)[J].电力系统自动化(Automation of Electric Power Systems),2009,33(23):69-74. [14]王卫平,王主丁,张昀,等(Wang Weiping,Wang Zhuding,Zhang Yun,et al).含分布式电源的配网无功优化混合算法(Hybrid algorithm for reactive power optimization in distribution networks with distributed generations)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2013,25(6):93-100. [15]余健明,张栋,姚李孝(Yu Jianming,Zhang Dong,Yao Lixiao).基于一种新待补偿点定位法的配电网络无功优化(Reactive power optimizayion of distribution network based on a new location algorithm for nodes to be compensated)[J].电网技术(Power System Technology),2004,28 (1):67-70. [16]Wang Zhuding,Shokooh Farrokh,Qiu Jun.An efficient algorithm for assessing reliability indexes of general distribution systems[J].IEEE Trans on Power Systems,2002,17 (3):608-614. Reactive Power Optimization of Weakly Meshed Distribution Networks Considering Upper Limits of Node Compensation HU Xiaoyang1,WANG Zhuding1,BIAN Yupeng2 In order to determine the node locations and compensation capacity limits reasonably,based on the features of genetic algorithm and weakly meshed distribution,a method of reactive power compensation distribution factors is proposed to deal with meshed distribution,which can determine the upper limits to node compensation.Both economic benefits and voltage quality are considered,by calculating the upper of node reactive power compensation capacity based on the largest economic benefits and voltage constraint,effectively compresses the search space.The practicality of the proposed algorithm is demonstrated using an IEEE33 test system. reactive power optimization;genetic algorithm;weakly meshed distribution networks;reactive power compensation distribution factor;upper limit to node compensation TM714.3 A 1003-8930(2016)02-0073-07 10.3969/j.issn.1003-8930.2016.02.12 胡晓阳(1991—),男,通信作者,硕士研究生,从事配网无功优化研究。Email:hxy20082209@sina.cn 王主丁(1964—),男,博士,教授,IEEE高级会员,从事电力系统运行与优化研究。Email:mmluck@yahoo.com 边昱鹏(1982—),男,本科,工程师,从事电力系统规划研究。Email:byp503@163.com 2014-05-07; 2014-11-203 弱环状配网无功优化算法









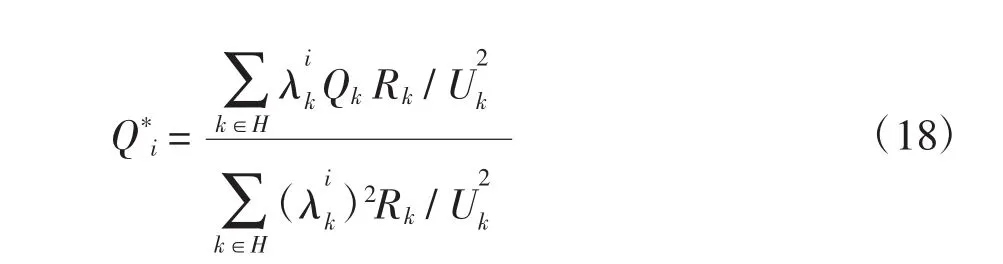
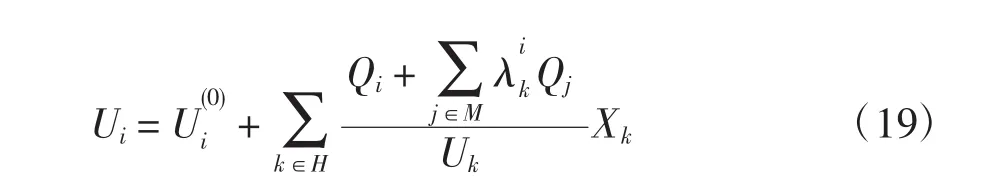






4 算例分析









5 结论
(1.State Key Laboratory of Power Transmission Equipment&System Security and New Technology,Electrical Engineering College of Chongqing University,Chongqing 400044,China;
2.Qujing Electric Power Supply Bureau,Yunnan Power Grid Company,Qujing 655000,China)

