考虑转向限制的电子海图最短距离航线自动生成方法
王涛,张立华,彭认灿,曹鸿博,3,姜林君3
(1.海军大连舰艇学院 海洋测绘系,辽宁 大连 116018;2.海军大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连116018;3.海军出版社,天津300450)
考虑转向限制的电子海图最短距离航线自动生成方法
王涛1,2,张立华1,2,彭认灿1,2,曹鸿博1,2,3,姜林君3
(1.海军大连舰艇学院 海洋测绘系,辽宁 大连 116018;2.海军大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连116018;3.海军出版社,天津300450)
针对当前航路二叉树方法求解最短距离航线未考虑舰船转向限制的问题,提出了一种顾及转向限制的最短距离航线自动生成方法。通过判断航线转向操纵缓冲区是否与碍航区相交,测试航线的可转向性;利用舰船转向次数、转向角度和转向半径,引入圆弧影响系数和回转速降系数,构建转向限制模型,实现了顾及转向限制的最短距离航线自动生成。实验结果表明:所提方法可排除当前最短距离航线生成方法中的不可行航线,优化了航线的转向次数和转向角度。
电子海图;碍航区;缓冲区;最短距离航线;转向限制
Kimeyesw a onrdds turn angles of the shortest route can be optimized. :electronic navigational chart;obstacle areas;buffer zone;shortest route;turning restriction
电子航海图(electronic navigational chart,ENC)已经广泛应用于海上航行,最优航线设计是电子航海图系统应用的重要内容[1-3]。最优航线是在保证舰船航行安全的前提条件下,使航线达到某种指标上的最佳[4-6]。民用船只的航线通常较为固定[1],但是在海上避难、搜救等应急行动以及军事行动中,需要灵活多变地选择航线[7]。近年来,最短距离航线设计成为众多学者关注的问题。张立华等提出了矢量电子海图平台下的计算机智能设计航线方法[8]。在此基础上,汪柱等提出了基于航路二叉树的航线自动生成方法[9]。曹鸿博等对航路二叉树方法进行了改进,采用碍航区路径的递归搜索、绕行优化以及动态求解等策略,实现了复杂碍航区的航线自动生成[10]。但是这些现有的方法在考虑航线距离最短时,仍忽视了一个很重要的问题,即舰船转向对最短距离航线的影响。这种影响主要表现在两个方面:1)得到的最短距离航线在实际中未必是真正可行的。现有的航路二叉树方法所生成的最短距离航线,在绕行碍航区的转向过程中,理想地采用直线路径,未考虑舰船需要循圆弧线逐渐转向的实际操纵,可能造成当前方法生成的航线在实际中无法真正安全航行。2)得到的航线未必是实际航行中最短的。当前方法仅理想地考虑直线距离上的最短,未有效顾及舰船转向次数、角度等对航线的影响。实际上,转向时会造成弧线航程增大,还可能引起船速降低,从而造成当前方法生成的最短距离航线在实际航行中未必是距离最短的。因此,研究顾及转向限制的电子海图最短距离航线自动生成具有理论和现实意义。
1 顾及转向限制的最短距离航线自动生成
1.1不可转向航线的排除
1.1.1舰船的圆弧转向
舰船具有一定的旋回半径和惯性,在循圆弧线连续不断的完成每次转向的过程中,弧线路径已经偏离原直线路径,从而造成当前方法生成的最短距离航线在实际中并不一定能够顺利实施转向[11-12]。如图1所示。

图1 舰船绕行碍航区转向示意图Fig.1 A sketch map of ship turning around obstacles
以当前方法生成的某一绕行碍航区O1的路径Pi-1PiPi+1为例,航段Pi-1Pi和航段PiPi+1的航向改变量θ叫做转向角[13]。根据转向操纵理论[13],舰船绕行碍航区O1由航段Pi-1Pi到航段PiPi+1时,无法沿直线直接突然转向,通常需沿圆弧路径连续、不断地完成转向,但已较大地脱离了原有的直线路径Pi-1PiPi+1,造成穿越碍航区O1,从而使得直线路径Pi-1PiPi+1在实际中并不真正可行。为保证航行安全,绕行的圆弧路径应在碍航区O1的外侧,为,但这样在A、B点处的路径仍是突然转向的,仍无法真正沿航行。实际操纵中,通常应进行三次转向才能绕行碍航区O1[13]:第1次转向起点为C1,终点为D1,从直线航段Pi-1C1连续转到较大弧线航段;第2次转向起点为D1,终点为C2,沿较大弧线航段航行;第3次转向起点为C2,终点为D2,从较大弧线航段逐渐转回直线航段。这样,舰船绕行碍航区O1的实际航行路径为和D2Pi+1,与直线航段Pi-1PiPi+1在地理位置上发生较大的变化。这种变化的路径仍可能会穿越碍航区(如图2中的穿越碍航区O2),从而造成当前方法生成的航线Pi-1PiPi+1并不可行。因此,在最短距离航线生成中,必须排除当前方法中实际上并不真正可行的航线。
1.1.2转向圆弧的确定及离散化处理
如图2所示,在舰船的某次转向过程中,为确定转向时的弧线路径和,只需计算圆心c2及点C1和D1、圆心c1及点D1和C2、圆心c3及点C2和D2的坐标。以圆心c1及点D1和C2的坐标求解为例(同理可求c2及C1和D1、c3及C2和D2的坐标),在以圆心c1(0,0)为原点、c1Pi为x轴正向的局部右手笛卡尔坐标系下,其计算公式如下
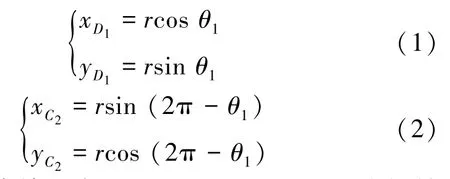
式中:r为定常旋回半径,θ1(θ1∈(0,π])为初始转向角,可由下式计算:


图2 转向圆弧的确定Fig.2 Calculation of turning arc
在求c2、C1、D1和c3、C2、D2的坐标时,需先求第1次转向时的转向角θ2和第2次转向时的转向角θ3,θ2和θ3可由下式计算(第3次转向时的转向角大小与θ2相同):

式中:由于∠Ac2E较小,可将其忽略。化简后θ2、θ3计算公式如下

为简便,对航线转向处的转向圆弧进行离散化处理。如图3所示,用A、P0、P1、P2、B这5个点的连线来逼近表示圆弧,内插采样点(如P0)个数n根据圆心角α和采样间隔Δα确定,公式如下


图3 圆弧的离散化处理Fig.3 The discretization processing method of the circular arc
1.1.3航线可转向性的判断
如图4所示,当前方法中,因障碍物位置的准确性、风(流、浪)等不确定性因素会影响航行安全[14-15],已对障碍区(或物)的范围进行了一定的扩充,称为碍航物缓冲区[8]。然而在舰船航行的过程中,舰船的操纵误差以及导航定位系统精度等因素(称为操纵不确定性),还会对航行路径造成一定的影响,这在舰船转向时是必须考虑的[16-17]。由此引起转向路径的不确定性,采用转向操纵缓冲区来表示。
对于给定的某一条计划航线,其可转向性N依赖于其转向操纵缓冲区B,数学模型可表达为N(B)[18]。一条航线的转向操纵缓冲区由一个或多个子转向操纵缓冲区组成,B={B1,B2…,Bn1},Bi为某次转向的子转向操纵缓冲区(i=1,2…,n1,n1为航线的转向次数)。若用1表示某次转向可行,用 0表示不可行。整条航线的可转向性N(B)由下式表达:


图4 航线转向操纵缓冲区生成示意图Fig.4 A sketch map of constructing turning areas of a routing
判断某次转向的可转向性,通过判断其子转向操纵缓冲区是否与碍航区相交来实现。设碍航区集合为O,对于某子转向操纵缓冲区Bi,如果Bi∩{O-O′}=φ(O′为Bi对应的当前绕行碍航区,且O′∈O),则N(Bi)=1。
判断各次转向的可转向性后,利用式(7)可解算整条航线的可转向性。如果N(B)=0,则该航线不可转向;如果N(B)=1,则该航线可转向。
1.1.4航线转向操纵缓冲区的生成
航线转向操纵缓冲区的生成过程类同于求取线缓冲区,在建立缓冲区时,应先确定缓冲区的宽度(以下简称缓冲距)。计算航线转向操纵缓冲区的缓冲距等同于利用舰船的转向操纵误差和导航定位误差对实施转向操纵时的航线误差进行估计。令舰船的操纵误差为σso,导航定位误差为σnl,并假设以上各个过程是相互独立的。根据误差传播定律求得缓冲距dbuffer算式如下
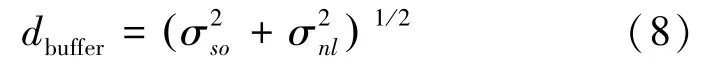
目前,线缓冲区生成算法主要有角平分线法、凸角圆弧法和线段基元叠置法[19-21]。角平分线法难以保证双线的等宽性,异常情况多,不易完备地实现[19];凸角圆弧法所生成的缓冲区边界可能出现尖角和凹陷等失真现象,且修正过程复杂[20]。线段基元叠置法能够有效克服前两种方法的不足[21],因此本文采用线段基元叠置法求航线转向操纵缓冲区。
以图4(a)为例,参照文献[21]中缓冲区的生成方法,航线某次转向的转向操纵缓冲区生成步骤如下:1)利用式(1)~(5)计算本次转向的转向圆弧,并利用式(6)对转向圆弧进行离散化处理,结果如图4(a)中的虚线所示;2)根据式(8)计算转向操纵缓冲区的缓冲距,并生成每一航段的基元缓冲区;3)将所有航段的基元缓冲区进行逻辑并运算,求出本次转向的航线转向操纵缓冲区。
但是,在上述的转向操纵缓冲区生成方法中会出现一个问题,即所求得的航线转向操纵缓冲区中存在不能够航行的区域,也就是转向操纵缓冲区与碍航区及其缓冲区的相交区域,转向不可行。为此,实际航行中要想在此处成功实施转向,还必须改变舰船转向时原来设定的弧线路径,使得航线转向操纵缓冲区与碍航区及其缓冲区不相交,但这其中将涉及较为复杂的几何运算,难以实现。本文采用一种等价的处理方法。如图4(b)所示,先对原碍航区的缓冲区进一步进行扩充处理,以预留出用于舰船转向的区域,再扩充的距离大小为dbuffer,从而使得转向操纵缓冲区与碍航区及其缓冲区不相交,转向可行。然后再采用上述的转向操纵缓冲区生成步骤生成航线转向操纵缓冲区。
1.2转向增加航程的计算
若某条航线未顾及转向限制的航程为S0,舰船转向增加的航程为STP,则顾及转向限制后的航程为S=S0+STP。假设航线的转向次数为n,则考虑转向限制后的航程可由下式计算:

舰船转向时,转向角度是另外一个必须考虑的重要因素。一般而言,转向角度越大,舰船的可操作性越差,相应增加的航程往往也越大。如图5所示,以往计算航程时,直接求解直线距离(Pi-1Pi+ PiPi+1)作为本次转向的航程,但这只是理想航程,并不是实际航行中的有效航程。在实际航行中,按照1.1.1节转向操纵理论所述,进行三次转向,转向时舰船的航行路径为和,则转向增加的航程可由下式计算:

化简后得
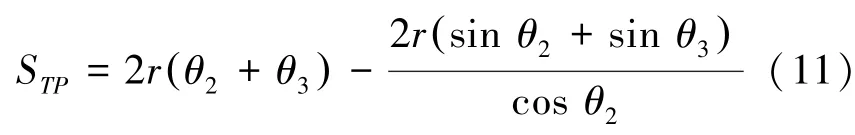
式中:r为定常旋回半径,θ2为第一次转向的转向角,θ3为第二次转向的转向角。

图5 转向限制模型Fig.5 Turn penalty model
在实际转向过程中,受人为因素、环境因素以及其他因素的影响,舰船的航行路径可能会偏离转向圆弧。为此,引入圆弧影响系数η来表示转向过程中实际航行路径与转向圆弧路径之间的偏差。
此外,舰船在转向过程中还存在速降问题,从而造成航行时间的增加,为更具可比性,将增加的时间归算成等效航程。通常以定常回转阶段舰船的航速V与回转开始时舰船直线航速V0之比来表征回转速降特征,称为回转速降系数,其计算公式如下[22]

式中:K′为旋回性指数;CN为舵的法向力系数;θ为转向角,rad。

2 实验与分析
2.1不可转向航线的排除
为了验证所提算法的有效性,本文以文献[22]中的舰船模型为实验模型,分别选取比例尺为1∶250 000和1∶800 000的两幅海图进行了相关实验,具体实验参数见表1。设置安全水深为14.0 m,实验结果如表2、图6和图7所示。

表1 实验参数Table 1 Experimental parameters

表2 不可转向航线的排除结果比对Table 2 Comparison of different methods for eliminating routes

图6 海图比例尺为1∶250 000Fig.6 A case of the chart scale is 1∶250 000

图7 海图比例尺为1∶800 000Fig.7 A case of the chart scale is 1∶800 000
从表2可以看出,未顾及转向限制时,在两幅海图上分别生成8条和15条绕行航线。但在实际航行中,还需要考虑舰船操纵性能的限制,从而使得某些绕行航线无法真正实施,这些航线应当被排除掉,真正可行的航线总数从而会减少。
在图6和图7中,折线是分别采用未顾及和顾及转向限制的方法为安全水深14.0 m的舰船自动生成的航线,图中的细实线折线为所有可绕行碍航区的航线,粗实线折线为最短绕行航线。对比图6(a)和图6(b)可知,未顾及转向限制的方法生成的最短距离航线ST(图6(a)中的粗实线折线)在顾及转向限制后(图7(b)中的虚线折线),因在碍航区 O3与 O4之间的虚线区域内无法实施转向,所以在实际航行中并不真正可行。因此,未顾及转向限制的方法生成的最短航线在实际中并不一定真正可行,而本文所提的顾及转向限制的方法生成的最短航线才真正可行。
2.2顾及转向限制的最短距离航线自动生成
为了进一步反映舰船转向对航线距离的影响,继续利用实验 2.1节中的数据,将安全水深由14.0 m改为12.0 m,碍航区范围由此变小,从而使得2.1节中所述两种方法生成的最短距离航线在实际中都真正可行。分别计算两种方法生成的最短航线的转向次数、最大转向角度和有效航程,实验结果如表3、图8和图9所示。
从实验结果可以看出,相比顾及转向限制的方法,未顾及转向限制的方法所生成的最短距离航线,其实际转向次数相对较多,最大转向角度相对较大,这会影响舰船转向的可操纵性;同时,其有效航程也相对较大,并不是实际航行中的最短距离航线。而采用本文所提方法生成的最短距离航线,其转向次数少,最大转向角度小,在顾及转向限制的情况下,实际航行的距离更短。

表3 最短距离航线自动生成结果比对Table 3 Comparison of different methods for the shortest distance routing

图8 海图比例尺为1∶250000Fig.8 A case of the chart scale is 1∶250000

图9 海图比例尺为1∶800 000Fig.9 A case of the chart scale is 1∶800 000
3 结论
通过理论分析及实验比对,得结论如下:
1)所提方法通过判断航线转向操纵缓冲区是否与碍航区相交,能够有效排除当前最短距离航线生成方法中的不可行航线,得到真正可行的最短距离航线。
2)所提方法在顾及转向限制的条件后,进一步优化了转向次数和角度,也使实际航行的距离更短。
当然,转向圆弧离散化处理中分段精度的不同会对结果产生一定的影响。另外,风、流等动态因素对舰船转向操纵的影响,还有待于以后进一步研究。
[1]CHANG K Y,JAN G E,PARBERRY I.A method for searching optimal routes with collision avoidance on raster charts[J].The journal of navigation,2003,56(3):371-384.
[2]RAFAL S.A new method of ship routing on raster grids,with turn penalties and collision avoidance[J].The journal of navigation,2006,59(1):27-42.
[3]ZHAO Yuxin,TANG Jiqiang,LI Gang,et al.Route design and automatic check in electronic chart display and information system[J].Journal of marine science and application,2004,3(1):33-36.
[4]王科.基于电子海图的航线设计研究[D].大连:海军大连舰艇学院,2004:1-2. WANG Ke.A study for designing navigation route based on ECDIS[D].Dalian:PLA Dalian Naval Academy,2004:1-2.
[5]谢兴澜.ECDIS中的航线设计与最优航法[D].大连:大连海事大学,2003:6-7. XIE Xinglan.Route planning&advanced navigation in ECDIS[D].Dalian:Dalian Maritime University,2003:6-7.
[6]汤青慧.基于电子海图的航线规划方法研究[D].青岛:中国海洋大学,2011:8. TANG Qinghui.Research on route planning method based on electronic chart[D].Qingdao:Ocean University of China,2011:8.
[7]芮震峰,应荣熔,李伟.基于直觉模糊数和相对贴近度军事航线优选[J].舰船科学技术,2014,36(1):144-157. RUI Zhenfeng,YING Rongrong,LI Wei.A methodology for military route selection using intuitionistic fuzzy numbers[J]. Ship science and technology,2014,36(1):144-157.
[8]张立华,朱庆,张安民,等.一种智能的最短航线构建方法[J].测绘学报,2008,37(1):114-120. ZHANG Lihua,ZHU Qing,ZHANG Anmin,et al.An intelligent method for the shortest routing[J].Acta geodaetica et cartographica sinica,2008,37(1):114-120.
[9]汪柱,李树军,张立华,等.基于航路二叉树的航线自动生成方法[J].武汉大学学报:信息科学版,2010,35 (4):407-410. WANG Zhu,LI Shujun,ZHANG Lihua,et al.A method for automatic routing based on route binary tree[J].Geomatics and information science of Wuhan university,2010,35(4): 407-410.
[10]曹鸿博,张立华,贾帅东,等.电子海图最短距离航线自动生成的改进方法[J].武汉大学学报:信息科学版,2011,36(9):1107-1110.CAO Hongbo,ZHANG Lihua,JIA Shuaidong,et al.An improved method for automatically building shortest route based on electronic chart[J].Geomatics and information science of Wuhan university,2011,36(9):1107-1110.
[11]李源惠,孙少鹏,于卫红.电子海图中计划航线可行性的自动判别[J].大连海事大学学报,2000,26(2):40-43. LI Yuanhui,SUN Shaopeng,YU Weihong.Auto evaluation of the feasibility of planned sea route in ECDIS[J].Journal of Dalian Maritime University,2000,26(2):40-43.
[12]尹相达.考虑施舵过程的本船转向避让时雷达标绘方法研究[J].中国水运,2011,11(7):15-16.
[13]陆儒德.舰船操纵与避碰[M].北京:海潮出版社,1993:34-40.
[14]BEKKER J F,SCHMID J P.Planning the safe transit of a ship through a mapped minefield[J].Jorssa,2006,22 (1):1-18.
[15]党莹.基于ECDIS大洋航线自动选择优化系统的研究及初步实现[D].上海:上海海事大学,2006:9-18.
[16]BIJLSMA S J.A computational method in ship routing using the concept of limited manoeuvrability[J].The Journal of Navigation,2004,57:357-369.
[17]郑中义.船舶自动避碰决策系统的研究[D].大连:大连海事大学,2000:23-25. ZHENG Zhongyi.Research on automatic decision-making system of vessel collision avoidance[D].Dalian:Dalian Maritime University,2000:23-25.
[18]张立华,刘雁春,朱庆,等.基于动态水位的航线可行性分析方法[J].武汉大学学报:信息科学版,2008,33 (9):892-895. ZHANG Lihua,LIU Yanchun,ZHU Qing,et al.Analysis of feasibility of routing based on changing water levels[J]. Geomatics and information science of Wuhan university,2008,33(9):892-895.
[19]吴华意,龚健雅,李德仁.缓冲曲线和边约束的三角网辅助的缓冲区生成算法[J].测绘学报,1999,28(4): 355-359. WU Huayi,GONG Jianya,LI Deren.Buffer curve and buffer generation algorithm in aid of edge-constrained triangle network[J].Acta geodaetica et cartographica sinica,1999,28(4):355-359.
[20]李金山,方金云.基于平面扫描的双线圆弧缓冲区生成算法[J].计算机工程与应用,2007,43(23):28-31. LI Jinshan,FANG Jinyun.Algorithm for line buffering based on plane sweep technique[J].Computer Engineering and Applications,2007,43(23):28-31.
[21]朱熀,艾廷华,王洪.基于条带扫描思想的线目标缓冲区快速构建[J].测绘学报,2006,35(2):171-176. ZHU Huang,AI Tinghua,WANG Hong.The buffer construction of line object based on the geometric scan idea [J].Acta geodaetica et cartographica sinica,2006,35 (2):171-176.
[22]李宗波,张显库,贾云.船舶转向过程中速度下降问题的研究[J].航海技术,2008(3):2-4.
本文引用格式:
王涛,张立华,彭认灿,等.考虑转向限制的电子海图最短距离航线自动生成方法[J].哈尔滨工程大学学报,2016,37(7):923-929.
WANG Tao,ZHANG Lihua,PENG Rencan,et al.Automatic generation of the shortest route of an electronic navigational chart considering turning restrictions[J].Journal of Harbin Engineering University,2016,37(7):923-929.
Automatic generation of the shortest route of an electronic navigational chart considering turning restrictions
WANG Tao1,2,ZHANG Lihua1,2,PENG Rencan1,2,CAO Hongbo1,2,3,JIANG Linjun3
(1.Department of Hydrography and Cartography,Dalian Naval Academy,Dalian 116018,China;2.Key Laboratory of Hydrographic Surveying and Mapping of PLA,Dalian Naval Academy,Dalian 116018,China;3.Navy Press,Tianjin 300450,China)
Aiming at the shortage of the shortest route generated by the existing binary tree method without considering a ship's turn restrictions,we propose a method for automatically generating the shortest route by considering turning restrictions.By determining whether the turn steering areas of sea routes intersect with obstacle areas,we tested the turning aspects of sea routes.We established a turning restriction model by considering turn times,turn angles,turn radii,arc coefficients,and coefficients for the slowdown effect and determined the shortest route by analyzing the turning restrictions.Experimental results demonstrate that sea routes generated by the existing shortest route method in which turns cannot be executed can be eliminated by the new proposed method and that the turn t
10.11990/jheu.201503059
P229
A
1006-7043(2016)07-923-07
2015-03-18.网络出版日期:2016-05-19.
国家自然科学基金项目(41471380,41171349);国家高技术研究发展计划项目(2012AA12A406).
王涛(1987-),男,博士研究生;张立华(1973-),男,教授,博士生导师.
张立华,E-mail:zlhua@163.com.
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160519.0901.002.html

