无动力模型自由飞试验过程仿真研究

刘朝君 孙颖飞 吴欣龙

中国飞行试验研究院

无动力模型自由飞试验过程仿真研究

刘朝君 孙颖飞 吴欣龙

中国飞行试验研究院

刘朝君（1986－）女，陕西西安人，工程师，硕士研究生，研究方向为无人机与模型自由飞试飞研究。

无动力模型自由飞试验因依靠载机携带，且模型留空时间较短，故其试验成本高，试验效率较低。本文利用程序对某无动力模型自由飞试验的过程进行预先仿真，分析模型与载机的分离过程，设计了相应的控制律，解决了模型投放的瞬态响应过大问题，同时通过仿真计算为机翼水平失速试验科目提供了升降舵舵指令变化曲线，为高精度完成试验科目提供参考，可提高试飞架次利用率，节省试验经费。

模型自由飞试验在航空技术发展过程中起着不可替代的重要作用，其最大特点是无人驾驶和全动态自由度，可进行一些危险科目的试验如失速尾旋、探索大迎角下的气动力特性、新气动力布局、以及在风洞中无法进行的试验科目等。模型自由飞试验按照模型是否带动力可分为带动力模型自由飞试验和无动力模型自由飞试验。无动力模型自由飞试验是由载机将模型带至试验空域并进行投放，待模型安全脱离载机后，操纵模型在真实大气中完成飞行科目的一种试验方法，其试验过程如图1所示。载机将模型投放后，操纵手采用常规遥控器和直接视觉的模式操纵模型进行试验，针对视距较远处操纵手可借助仪表操纵方式完成试验。

无动力自由飞模型需靠母机携带到空中投放，且模型留空时间较短，在一次飞行中不能进行重复性试验，故其试验成本高，试验效率较低。因此降低试验风险，提高操纵手在试验动作段的操纵精度，提高试验有效性已经成为无动力模型自由飞试验的重要需求目标。本文根据某自由飞模型气动特性及试验要求，设计了一种无动力模型自由飞的试验方案：投放模型后0～10s模型沿一个航迹角下滑至试验空域，10s后操纵升降舵使模型以稳定的减速率减速直至模型到达失速状态。利用程序对该试验过程进行仿真，分析模型投放瞬间的姿态，规避模型与载机的碰撞风险，并可得出在模型在减速过程中的升降舵的操纵曲线及操纵时间，为飞行试验提供参考，提高试飞架次利用率。

建立数学模型

本文不考虑载机螺旋桨滑流及流场对模型的干扰，主要根据模型的重量、重心、惯量矩，结合风洞实验数据、气动力及六自由度运动方程仿真计算投放后模型在自由流场中质心的运动轨迹。

气动力的表达式中考虑了迎角、侧滑角、马赫数和气动操纵面偏角的影响，具体表达式如公式（1）：

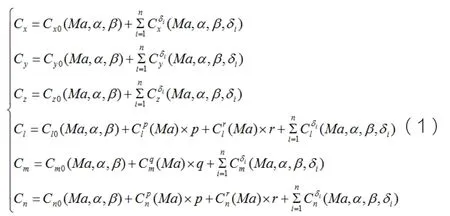
仿真动力学模型采用六自由度刚体动力学方程。其表达式为：

试验过程仿真

稳定下滑段

根据该自由飞模型投放要求，在投放时刻取模型投放速度为120km/h，投放高度为1400m，投放时模型的姿态角为－7°。本文忽略侧滑对模型横航向运动的影响，仅分析模型纵向运动特性。飞机在升力、重力、阻力和俯仰平衡力矩的共同作用下，t 时刻以真速V下滑，下滑角为γ，俯仰角为θ，则在航迹坐标系上，模型受力关系为：

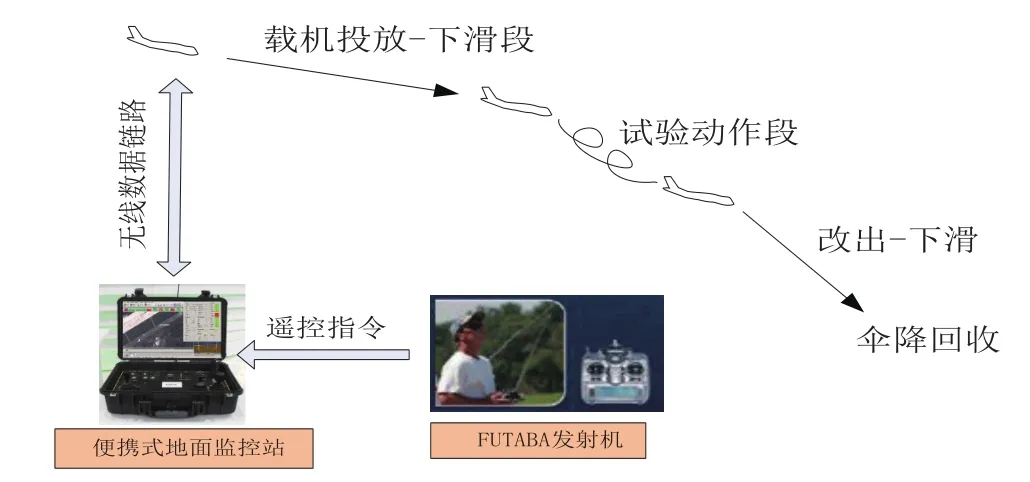
图1　无动力模型自由飞试验过程图

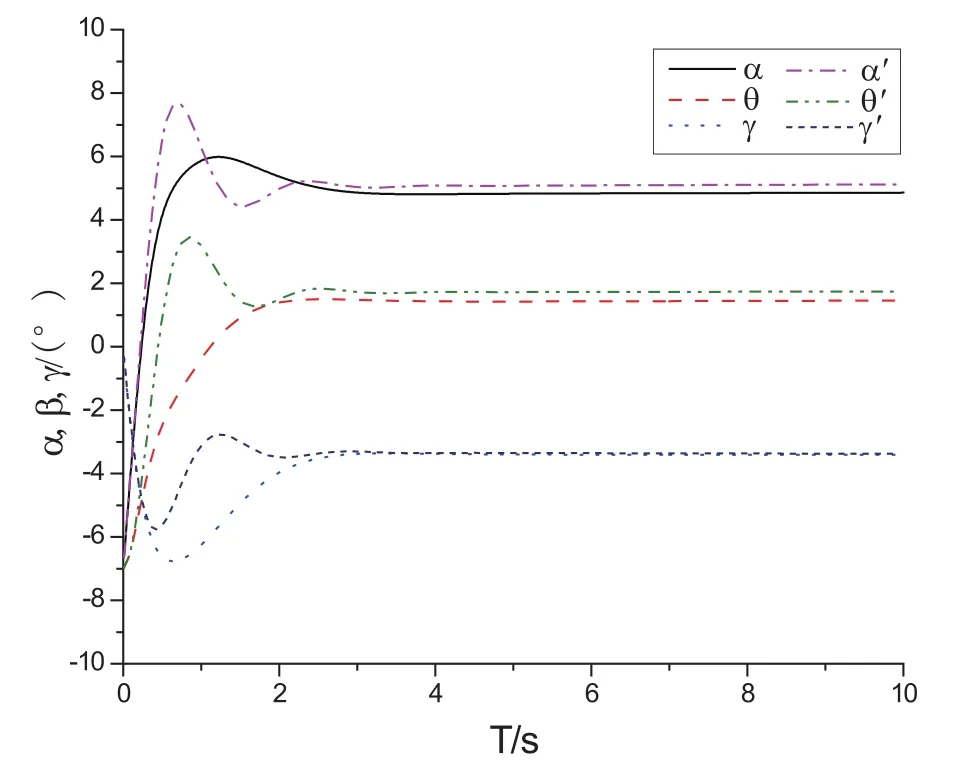
图2　增加控制律前后模型下滑轨迹对比曲线

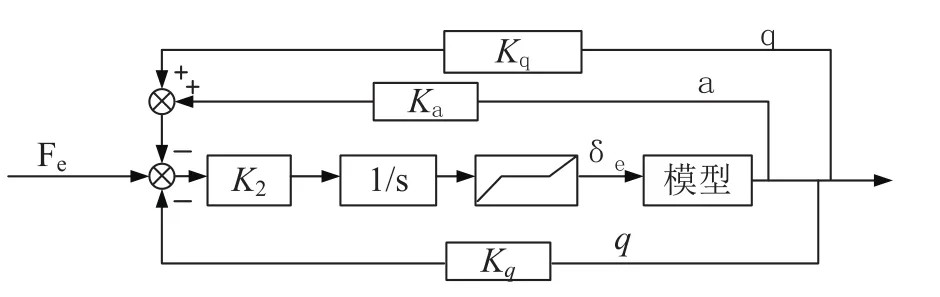
图3　模型纵向控制框图

若模型为定常下滑飞行，则γ和V不变，可得：

根据模型投放速度及高度，结合模型质量可推出：

稳定下滑时俯仰力矩系数为：

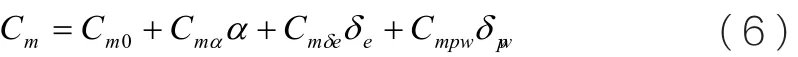
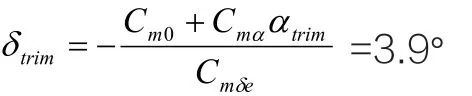
结合模型挂飞状态的初始条件α=－7°，θ=－7°，给出固定升降舵偏度δtrim=3.9°进行模型下滑轨迹仿真，可得到仿真曲线如图2中α、θ、γ所示，从这三个参数曲线可以看出给定升降舵舵偏后，模型姿态调整至稳定状态后即开始定常下滑。因模型投放瞬间姿态角变化较大，存在与载机的投放挂架发生碰撞的隐患，因此应设计控制律对模型投放时纵向增稳，防止模型抬头响应过大，控制律框图如图3所示，增加控制律后模型的姿态变化如图2中α'、θ'、γ'所示，经对比可以看出该控制律可有效控制模型瞬态响应。

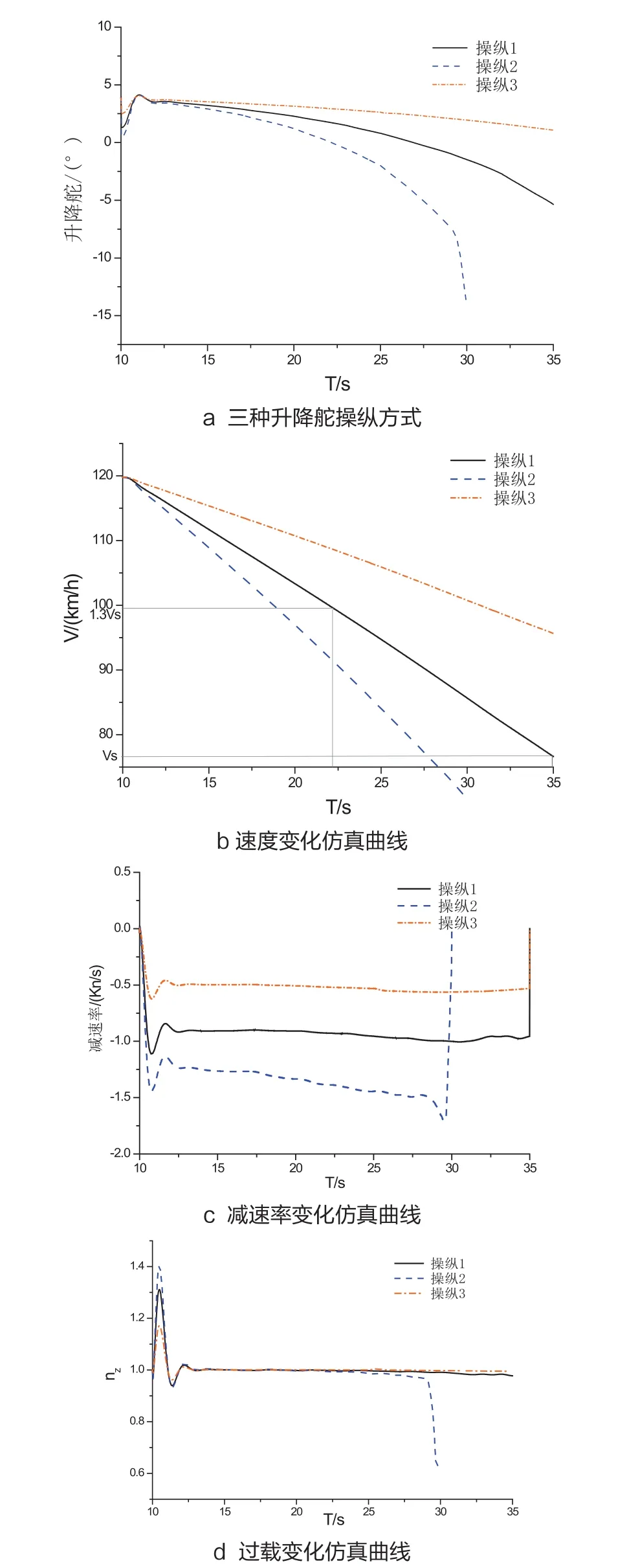
图4　三种操纵方式引起的模型状态变化曲线

机翼水平失速段

中国民用航空条例（CCAR）第25 部要求在确定飞机的失速速度中，以1.3Vs（Vs 为失速速度设计值）的速度配平飞机作直线飞行，随后操纵升降舵使飞机在－0.5～－1.5kn/s范围内以不同的减速率减速直至失速。本文模拟在定常下滑后，操纵模型进行无动力平飞失速的过程。仿真过

程设计了三种操纵方式（拉杆动作），如图4－a所示，分别通过计算得出这三种操纵方式引起的飞机响应，如图4－b～d所示。

从图4可以看出，从稳定下滑阶段改为1g失速时，操纵1从在20s内缓慢拉杆5.2°，减速率约为1kn/s；操纵2拉杆较快，在20s内拉杆18°，减速率在1.25～1.5kn/s；操纵3拉杆在20s内仅拉杆2°，减速率约为0.5kn/s，虽满足1g失速要求，但从图8可以看出，35s时模型仍未失速，因此该操纵方式会造成拉杆时间过长，模型滑行距离过大，造成模型离操纵手距离较远引起操纵困难。

经分析，这三种操纵方式均满足机翼水平失速的操纵要求，其中操纵1与试飞需求最接近，升降舵在减速段满足三次方函数关系：

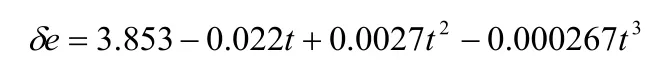
模型从1.3Vs到Vs的减速时间约为10.5s。该仿真结果可在实际机翼水平失速试飞中直接为操纵手精准的控制模型提供支持，为模型的失速试验提供参考。

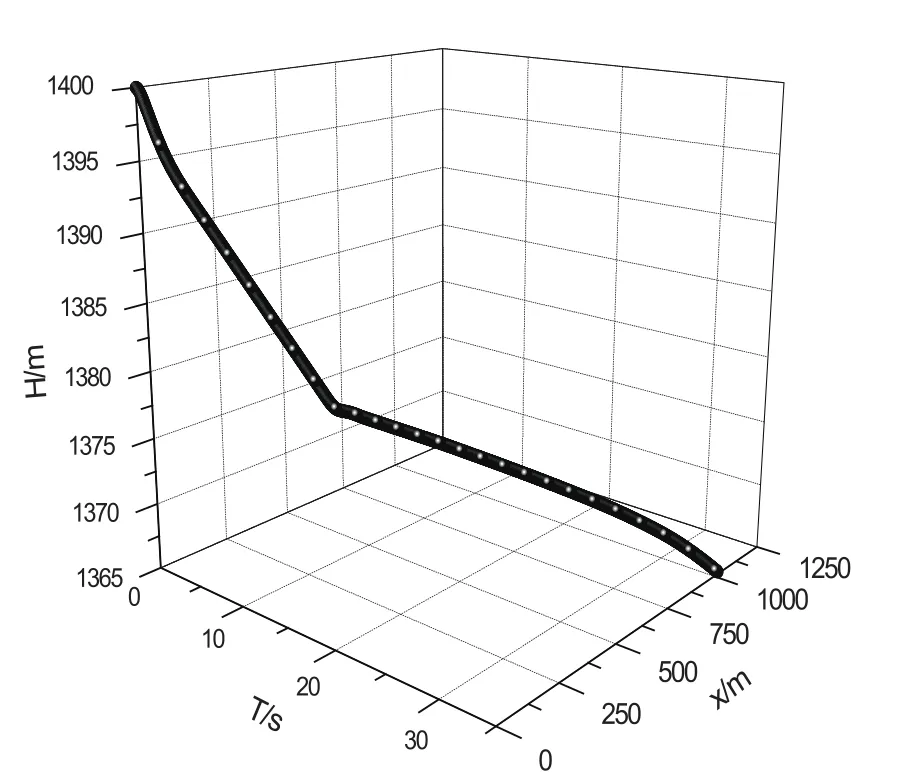
图5　模型轨迹仿真曲线

模型运动轨迹图

在地轴系，模型的运动学方程为：

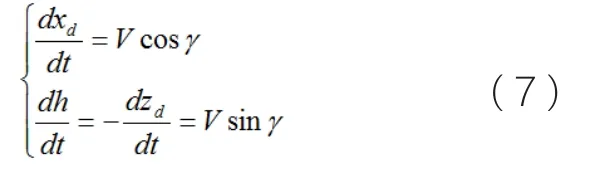
利用公式（7）计算模型下滑过程及1g失速过程（按照操纵1）的运动轨迹，如图5所示。从图中可以看出，模型水平失速过程中带有一定的下滑角。

结束语

本文利用程序对某模型自由飞试验过程进行了仿真计算，保证了模型与载机的安全分离，同时为机翼水平失速试验科目提供了舵指令变化曲线及拉杆时间，为高精度完成试验科目提供参考。因仿真过程未考虑模型横侧向的气动特性及风速等因素，真实飞行情况还待进一步研究。