快速反射镜姿态角的高精度解算
薛乐堂,陈 涛,徐 涛,2,刘廷霞,李 博
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
快速反射镜姿态角的高精度解算
薛乐堂1,2*,陈涛1,徐涛1,2,刘廷霞1,李博1
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
为了提高跟瞄转台出射激光的指向精度,研究了快速反射镜(FSM)姿态角与转台跟踪误差间的关系,提出了FSM姿态角的高精度解算方法。介绍了跟瞄转台出射激光的光路特点和FSM的工作原理;确定了坐标系中入射光与出射光的方向,依据坐标变换理论和光的反射定律,建立了FSM反射镜姿态角与转台跟踪误差间的函数关系。然后,推导出姿态角的解析表达式,描述了姿态角的空间分布规律,并从解析表达式中推出了近似表达式,确定了近似表达式引入的指向误差。最后,通过指向精度实验验证了姿态角解算方法的正确性。实验结果表明:在跟踪误差不超过(A12.9′,E13.5′)时,应用姿态角解析表达式和近似表达式均能取得优于2.5″的指向精度;跟踪误差增大为(A38.6′,E37.8′)时,解析表达式对应的指向误差仍低于2.5″,而近似表达式对应的指向误差迅速增大为13.2″。得到的结果显示:FSM姿态角的解析表达式不存在原理误差,在任意跟踪误差下均能使出射激光具有高精度指向能力,且其形式简洁,满足伺服控制器快速运算的要求。
快速反射镜;跟瞄转台;指向精度;姿态角;解析表达式
*Correspondingauthor,E-mail:xueletang2008@sina.com
1 引 言
在载车行进过程中对目标进行高精度跟瞄打击已成为光电对抗技术的重要发展方向[1,2]。跟瞄转台的大惯量特点使其不能很好地消除路面颠簸对跟踪精度的不利影响,降低了出射激光的指向精度。为了解决这个难题,除了提高转台的抗干扰性能,还要在系统设计时引入快速反射镜(Fast Steering Mirror,FSM)装置。FSM是通过快速调整反射镜的姿态角来实时控制光束方向的装置,它具有体积小、结构紧凑、响应速度快、精度高、带宽高等优点[3-7]。在光电对抗系统中,FSM常被用于迅速修正由跟瞄转台跟踪误差引起的出射激光的方向误差,以提高出射激光的指向精度。
FSM的姿态角直接影响出射激光方向,对其进行高精度解算是FSM控制的核心问题。FSM姿态角的大小与转台的跟踪误差成一定的函数关系,但目前对这一关系的研究并不透彻:相当多的文章认为两者符合2倍关系[8-12],但事实证明这种观点过于粗略甚至是不准确的;有人分别从几何分析与坐标变化的角度推导了描述两者关系的近似公式[13-14],其结论与实验数据的拟合结果相吻合,但因推导过程存在近似环节而不具有普适性。虽然在跟踪误差较小时利用近似公式能获得不错的指向精度,但由于近似公式的使用范围、误差影响等不确定,在跟踪误差超过一定范围后仍使用近似公式求解FSM姿态角可能导致出射激光错失目标。
为解决上述难题,获得准确的FSM姿态角表达式,本文研究了FSM姿态角与转台跟踪误差间的关系,推导出形式简洁的FSM姿态角的数学解析式。实验中,使用文中推导出的公式求解FSM姿态角,以验证其实际效果。
2 FSM修正出射激光方向的原理
如图1所示,激光束经过转台内部库德镜组的逐级反射,最后沿平行于转台水平轴的方向入射进FSM,经FSM反射后沿平行于转台视轴的方向出射,从而使出射激光随转台视轴指向目标。显然,转台跟瞄目标时存在的跟踪误差将影响出射激光对目标的指向精度。
为克服跟踪误差对指向精度的不利影响,可以根据转台跟踪误差的大小迅速地调整FSM的姿态角,使经FSM反射后的出射激光始终响应跟踪误差的变化,保持对目标的高精度指向。
3 快速反射镜姿态控制
3.1FSM的初始位置及其姿态角
在对转台光路系统精密装调时,将FSM成45°角安装在光路中,使平行于转台水平轴入射的激光束经FSM反射后沿平行于转台视轴的方向出射,则该45°角位置定义为FSM的初始位置α1,见图2。
转台跟踪误差的存在使得视轴不能准确指向目标(两者间的偏角为δ),导致原本平行于视轴方向出射的激光束也不能准确地指向目标。为保证出射激光的指向精度,可使FSM先从初始位置α1出发绕其自身方位轴旋转角β到位置α2,再绕其俯仰轴转动角γ到位置α3,见图2。其中β、γ即为表征FSM空间位置的姿态角。只要δ、β、γ满足一定关系,经FSM后的出射激光束就能再次准确指向空间目标。本文将重点研究δ、β、γ之间的关系。

图1 系统光路中的FSMFig.1 FSM in optical paths of whole system


图2 FSM姿态角与出射光方向Fig.2 Attitude angles of FSM and direction of emergent light
3.2坐标系及姿态角的定义
转台坐标系o(O)-xyz:见图2,观察者站在转台后方,目光沿视轴前视。水平轴方向定义为oz轴,向右为正向;视轴方向定义为ox轴,指向目标为正向;oy轴由右手定则确定,当视轴水平放置时,oy轴垂直于水平面并指向天顶。



3.3转台坐标系下的入/出射光方向
入射激光与出射激光始终在坐标系原点交汇,除坐标原点外,只要分别确定入射光路、出射光路上的一点,即可确定它们的方向。
3.3.1入射光方向

3.3.2出射光方向


图3 跟踪误差与脱靶量的关系Fig.3 Relationship between tracking error and miss distance

(1)
式(1)中A、E的单位是角秒,Sp像元尺寸,其单位为微米(μm),f为光学系统焦距,其单位为毫米(mm)。
令
K=Sp×10-3÷f×(180÷π×3 600),
(2)
则式(1)简化为

(3)
由于文章幅面限制,下文仍以A、E表示转台跟踪误差,只在具体实验时用MDa、MDe来具体计算A、E值的大小。
为建立入射光、出射光之间的数学关系,设目标P2距原点o的距离亦为L,则P2在转台坐标系内的极坐标为(A,E,L),直角坐标为P2(LcosEcosA,LsinE,LcosEsinA)。
3.4FSM坐标系下的入/出射光方向

3.4.1转台坐标系到FSM坐标系的坐标变换
由图2知,逆着oy轴俯视转台时,将转台坐标系o-xyz绕其oy轴逆时针旋转-45°,得FSM坐标系o-x1y1z1,负号表示坐标系旋转方向与前面定义的β角正向相反;将坐标系o-x1y1z1绕其轴oy1旋转β角,得坐标系o-x2y2z2;将坐标系o-x2y2z2绕其轴oz2旋转γ角,得坐标系o-x3y3z3。
设空间目标P在坐标系o-xyz、o-x1y1z1、o-x2y2z2、o-x3y3z3下的坐标分别为(x,y,z)、(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),则点P在不同坐标系下的坐标之间满足式(4)、(5)、(6)所示关系。

(4)
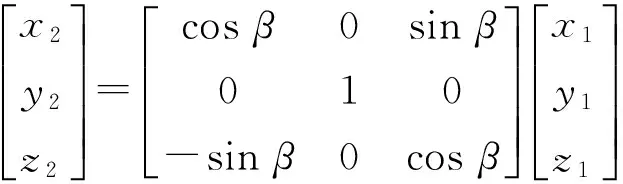
(5)

(6)
在坐标变换过程中,后一次变换是在前一次变换的基础上进行的,连续两次变换的合成变换矩阵等效于用后一次变换的变换矩阵左乘前一次的变换矩阵,因此空间点的坐标从转台坐标系o-xyz到FSM坐标系o-x3y3z3的变换矩阵T如式(7)所示,其中T(-45°)、Tβ、Tγ分别对应式(4)、(5)、(6)中的坐标转换矩阵,且T(β-45°)等效于TβT(-45°)。

(7)
3.4.2入/出射光路上点的FSM坐标
P1在转台坐标系下的直角坐标为P1(0,0,-L),则P1在FSM坐标系内的坐标为

(8)
P2在转台坐标系下的直角坐标为P2(LcosEcosA,LsinE,LcosEsinA),则P2在FSM坐标系内的坐标为

(9)
3.5光的反射


(10)
3.6FSM姿态角的解算
3.6.1姿态角的解析表达式


图4 FSM对出射光的反射Fig.4 Reflection of emergent light by FSM
sinEsinγ+cosAcosEcosγcos(β-45°)+cosEcosγsinAsin(β-45°)=-cosγsin(β-45°),
(11)
sinEcosγ-cosAcosEsinγcos(β-45°)-cosEsinγsinAsin(β-45°)=-sinγsin(β-45°),
(12)
cosEsinAcos(β-45°)-cosEcosAsin(β-45°)=cos(β-45°),
(13)
由式(13)可得
cosEcos(A-β-45°)=cos(β-45°),
(14)
进而得到β的解析表达式(15)。

(15)
β在跟踪误差A-E空间的分布见图5,因为E值较小,故其分布具有在E方向基本不变的特点。
由式(11)、(12)可得
tan 2γ=tanE/cos (A-β+45°),
(16)
进而得到γ的解析表达式(17)。

(17)
γ在跟踪误差A-E空间的分布见图6,因为A、E值较小,故其分布具有在A方向基本不变的特点。
3.6.2姿态角的近似表达式
在工程实践中,通常采用近似公式(18)、(19)计算FSM的姿态角[13-14],该公式并不准确,虽有实验数据验证其在跟踪误差A、E较小时的可行性,但缺乏充分的理论支持。本文从前面建立的解析表达式出发,通过必要的近似得到该近似公式。
转台伺服系统通常可以达到30′以内的跟踪误差,保证目标到视轴的方位偏角A、俯仰偏角E均小于30′,即A≤30′,E≤30′;而FSM转动范围的设计指标通常在10′以内,则FSM绕其方位轴的转角β≤10′,绕其俯仰轴的转角γ≤10′。
当E≤30′时,cosE≈1,则式(14)可近似为cos(A-β-45°)=cos(β-45°),从而有
β=A/2,
(18)
这从β真值的空间分布图5也能看出:E对β真值的影响很小,当E值符合一定条件时,β可看作只跟A有关,且满足式(18)。


(19)

(a)任意(A,E)时的β真值(a)True value of β with arbitrary A,E
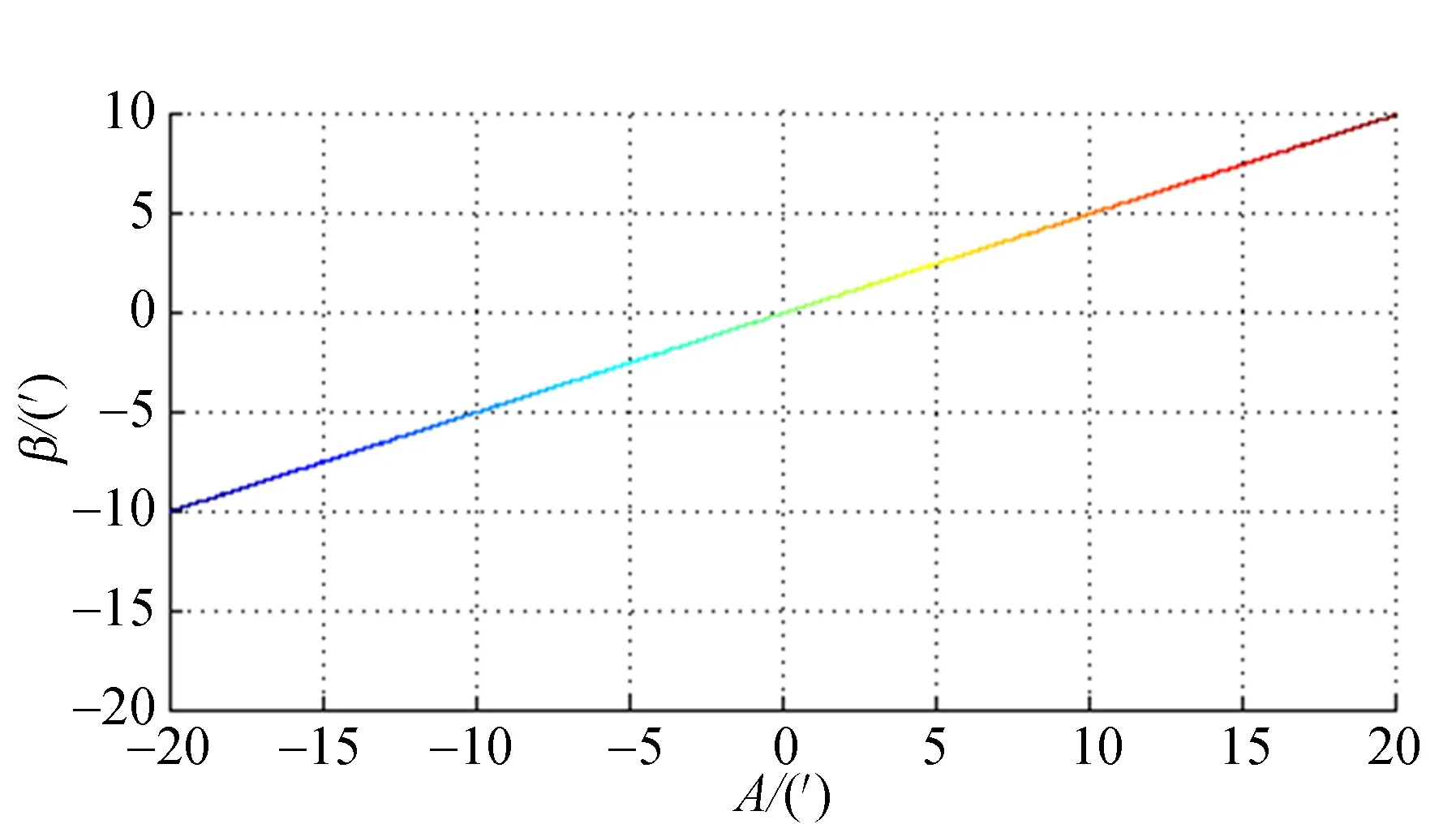
(b)沿E方向平视时β真值的3D分布(b)3D distribution of β true value when viewing along E direction图5 姿态角β在A-E空间的分布Fig.5 Distribution of attitude angle β in the A-E space

(a)任意(A,E)时的γ真值(a)True value of γ with arbitrary A,E

(b)沿A方向平视时γ真值的3D分布(b)3D distribution of β when viewing along A direction图6 姿态角γ在A-E空间的分布Fig.6 Distribution of attitude angle γ in the A-E space
3.6.3近似表达式引起的指向误差
使用近似公式(18)、(19)来计算β、γ,FSM实际位置与理论位置之间必将出现误差,从而影响出射激光的方向,产生指向误差。出射激光在方位方向、俯仰方向的指向误差分布分别见图7、图8。

(a)β近似值引起的激光指向的方位误差(a)Azimuth error of laser pointing caused by β approximate

(b)沿A方向平视时激光指向方位误差的3D分布(b)3D distribution of azimuth error of laser pointing when vieving along A direction图7 近似公式引起的方位指向误差Fig.7 Azimuth pointing error caused by approximate formulas
从图7可以看出,出射激光的方位指向误差大小与A近乎无关,主要与E的大小有关,当-10.7′ 从图8可以看出,出射激光的俯仰指向误差大小与A、E均相关,只有A、E均较小(由A-E坐标面的原点向外扩展,不超过图8中黑线)时,出射激光的俯仰指向误差才能控制在1角秒以内,若超出这个范围,俯仰指向误差将成抛物线状迅速增大。 3.6.4姿态角表达式的使用原则 近似表达式(18)、(19)形式简单、计算量小,在跟踪误差A、E较小时,具有较高的指向精度,但跟踪误差A、E超过一定范围后,使用近似公式将带来很大的指向误差;解析表达式(15)、(17)的形式较近似表达式略微复杂,但能避免引起指向精度的原理误差。故应根据指向精度的具体要求、FSM姿态角的范围、转台跟踪误差的大小来选择使用解析表达式还是近似表达式,或是统一使用解析表达式来解算FSM姿态角。 (a)γ近似值引起的激光指向的俯仰误差(a)Pitch error of laser pointing coused by γ approximate (b)俯视时激光指向俯仰误差的3D分布(b)3D distribution of pitch error of laser pointing by overlooking图8 近似公式引起的俯仰指向误差Fig.8 Pitch pointing error caused by approximate formulas 为验证FSM姿态角的解析表达式、近似表达式的正确性与实际应用效果,设计并进行了指向精度实验。 由于该实验意在验证出射激光指向误差与跟踪误差A、E之间的关系,故需设法降低其它误差源对实验结果的影响。在正式实验前,需校准光路,使进入FSM的入射光严格平行于转台水平轴,并测定FSM的位置定点精度。 4.1光路校准 用数引定点的方式将FSM定位到其45°初始位置,再通过光路校准的必要方法与步骤,确保指示激光沿转台水平轴方向入射到FSM,经FSM反射后的出射激光平行于视轴出射,保证两者的平行度不大于0.3″。 通过光路校准可有效减小并校验射入FSM的入射激光的方向误差。 4.2定点实验 在定点实验中,分别用不同的姿态角作为引导值,用数引模式控制FSM进行定位,测试定位过程中的响应时间与稳态误差。 FSM在方位方向的稳态误差为0.33″,响应时间为0.19 s;在俯仰方向的稳态误差为0.17″,响应时间为0.24 s。实验结果表明FSM具有定点误差小、响应迅速的特性。 4.3指向精度实验 图9 指向精度实验原理图Fig.9 Principle diagram of pointing accuracy experiment 图10 指向精度实验使用的靶板Fig.10 Target plate used for pointing accuracy experiment 试验在某跟瞄转台上进行,其光学成像系统的焦距为480 mm,所用的成像CCD的像元尺寸为20 μm×20 μm,根据式(2)可知K值为8.594 4。 试验过程如下: (1) 在距离转台1 km处设置靶板,靶板中心安装一个亮度可调的点光源,如图10所示; (2) 用数引模式控制转台,改变视轴指向,使靶板上的点光源成像在转台的CCD靶面上,且呈米字形分布于CCD靶面中心周围; (3) 对于每个测量点,分别记录目标的脱靶量MDa、MDe,根据式(3)将其换算成跟踪误差A、E,再用FSM姿态角的解析表达式(15)(17)及近似表达式(18)(19)解算出FSM的姿态角β、γ,并控制FSM进行偏转,记录1 km外靶板上所接收的激光光斑中心相对于点光源的距离x、y。 (4) 出射激光在方位方向上的指向误差 ΔA=x×10-3/1 000/π×180×3 600, (20) 出射激光在俯仰方向上的指向误差 ΔE=y×10-3/1 000/π×180×3 600, (21) 其中ΔA、ΔE的单位为角秒。 试验数据见表1。为方便对比,在其它条件相同时,测量分别使用解析表达式与近似表达式求解FSM姿态角时的出射激光指向误差。 从表1可以看出:跟踪误差小于(A12.9′,E13.5′)时,解析表达式与近似表达式对应的指向误差均在2.5″以下;跟踪误差为(A38.6′,E37.8′)时,使用解析表达式算得的指向误差仍不超过2.5″,但使用近似表达式得到的指向误差最大可达13.2″。 解析表达式(15)、(17)消除了求解FSM姿态角的原理误差,但激光射入FSM时存在的入射方向误差、FSM的控制误差及光斑位置的测量误差,这些误差将使实测的指向误差在理论的零误差附近波动,若要实现更高的指向精度,需设法进一步降低这3项误差。 表1 指向精度实验数据 本文根据跟瞄转台出射激光应具有高进度指向能力的要求,建立了FSM姿态角与转台跟踪误差之间的数量关系,获得了形式简洁的FSM姿态角的解析表达式,然后通过近似等效解析表达式,得到FSM姿态角的近似表达式,并指出了近似求解公式的局限性。实验结果表明:当跟踪误差A、E分别为38.6′、37.8′时,使用解析表达式解算FSM姿态角,可将出射激光的指向误差控制在2.5″内,而此时使用近似表达式解算时,对应的指向误差为13.2″。FSM姿态角解析表达式满足出射激光在任意跟踪误差下均以高精度指向目标的要求,极大地提高了出射激光的指向精度。 [1]张振东. 车载光电设备动态跟踪技术研究[D].北京:中国科学院大学,2013. ZHANG ZH D.Theresearchofvehiclephotoelectricequipmentdynamictrackingtechnology[D]. Beijing: University of Chinese Academy of Sciences, 2013.(in Chinese) [2]邓耀初. 基于快速反射镜的光束指向稳定技术[D].西安:西安电子科技大学,2008. DENG Y CH.Thelight-beampointingstabilitytechniquesbasedonFSM[D]. Xi’an: Xidian University,2008.(in Chinese) [3]徐新行,高云国,杨洪波,等. 车载大口径刚性支撑式快速反射镜[J].光学 精密工程,2014,22(1):117-124. XU X H, GAO Y G, YANG H B,etal.. Large-diameter fast steering mirror on rigid support technology for dynamic platform[J].Opt.PrecisionEng., 2014, 22(1):117-124.(in Chinese) [4]周子云,高云国,邵帅,等.采用柔性铰链的快速反射镜设计[J].光学 精密工程,2014,22(6):1547-1554. ZHOU Z Y, GAO Y G, SHAO SH,etal.. Design of fast steering mirror using flexible hinge[J].Opt.PrecisionEng., 2014,22(6):1547-1554.(in Chinese) [5]PALOSZ A.Higherorderslidingmodecontroloflaserpointingfororbitaldebrismitigation[D]. Master Degree Thesis: The University of Alabama in Huntsville,2013. [6]CHO M, CORREDOR A, DRIBUSCH C,etal..Performance prediction of the fast steering secondary mirror for the giant magellan telescope[C].SPIE,AstronomicalTelescopes+Instrumentation.InternationalSocietyforOpticsandPhotonics, 2012:844424-844424-13. [7]ULANDER K.Two-axisbeamsteeringmirrorcontrolsystemforprecisionpointingandtrackingapplications[D]. Master Degree Thesis: Lawrence Livermore National Laboratory, 2006. [8]胥青青,纪明,雷霏霖,等. 光电稳瞄二级稳定系统性能分析及测试[J]. 应用光学,2014,35(1):17-21. XU Q Q, JI M, LEI F L,etal.. Performance analysis and test of opto-electronic two-level stabilization system [J].JournalofAppliedOptics,2014,35(1):17-21. (in Chinese) [9]胥青青,刘伟,纪明,等. 远程红外探测系统瞄准线高精度稳定技术[J]. 红外与激光工程,2014,43(11):3646-3650. XU Q Q, LIU W, JI M,etal.. Line-of-sight high-precision stabilization technology of remote infrared detection system[J].InfraredandLaserEngineering, 2014,43(11):3646-3650. (in Chinese) [10]田福庆,李克玉,王钰,等. 压电驱动快速反射镜的自适应反演滑模控制[J]. 强激光与粒子束,2014,26(1): (011011)1-5. TIAN F Q, LI K Y, WANG J,etal.. Adaptive backstepping sliding mode control of fast steering mirror driven by piezoelectric actuator[J].HighPowerLaserandParticleBeams, 2014,26(1):(011011)1-5. (in Chinese) [11]ZHOU Q K, BEN-TZVI P, FAN D P,etal.. Design of fast steering mirror systems for precision laser beams steering[C].IEEE,InternationalWorkshoponRoboticandSensorsEnvironments, 2008:144-149, DOI:10.1109/ROSE.2008.4669196. [12]MATTOS L S , DELLEPIANE M , CALDWELL D G. Next-generation micromanipulator for computer-assisted laser phonomicrosurgery[C].IEEE, 33rdAnnualInternationalConferenceoftheIEEEEMBS, 2011:4555-4559, DOI:10.1109/IEMBS.2011.6091128. [13]彭树萍,陈涛,刘廷霞,等. 激光发射系统快速反射镜的光线反射过程[J].光学 精密工程,2015,23(2):378-386. PENG SH P, CHEN T, LIU T X,etal.. Reflection process of fast-steering mirror of laser launching system[J].Opt.PrecisionEng., 2015, 23(2):378-386.(in Chinese) [14]LI J, XIU J H, HUANG P,etal.. Non-linear compensation algorithm of LOS locating in aerial remote sensor[C].IEEE,InternationalConferenceonElectronicandMechanicalEngineeringandInformationTechnology, 2011, 5:2454-2457, DOI: 10.1109/EMEIT.2011.6023539. [15]周子云. 多波段激光发射方向直接检测与校正方法研究[D].北京:中国科学院大学,2014. ZHOU Z Y.Researchondirectmonitorandcorrectionmethodsforemitteddirectionofmulti-wavelengthlaserbeam[D]. Beijing: University of Chinese Academy of Sciences, 2014.(in Chinese) [16]陆震. 高等机械原理[M]. 北京:北京航空航天大学出版社,2001. LU ZH.SeniorMechanicalTheory[M]. Beijing: Beihang University Press ,2001.(in Chinese) [17]薛向尧,高云国,韩光宇,等. 水平式经纬仪指向误差的统一补偿技术[J].光学 精密工程,2011,19(7):1524-1530. XUE X Y, GAO Y G, HAN G Y,etal.. Total correction method of pointing error for level mounting theodolite[J].Opt.PrecisionEng., 2011,19(7):1524-1530.(in Chinese) 薛乐堂(1980-),男,河南社旗人,博士研究生,助理研究员,2004年于北京航空航天大学获得学士学位,2009年于中国科学院研究生院获得硕士学位,主要从事光电跟踪设备的伺服控制技术研究。E-mail:xueletang2008@sina.com 导师简介: 陈涛(1965-),男,内蒙古赤峰人,博士,研究员,博士生导师,1987年于大连理工大学获得学士学位,1990年、2007年于中国科学院长春光学精密机械与物理研究所分别获得硕士、博士学位,主要从事光电精密跟踪测量技术的研究。E-mail:chent@ciomp.ac.cn (版权所有未经许可不得转载) High-precision calculation for attitude angles of fast steering mirror XUE Le-tang1,2*, CHEN Tao1, XU Tao1,2, LIU Ting-xia1, LI Bo1 (1.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China; 2.UniversityofChineseAcademyofSciences,Beijing100049,China) To improve the pointing precision of output laser for a tracking turntable, the relationship between the attitude angles of a Fast Steering Mirror (FSM) and the tracking error of a tracking turntable was researched and a high precision calculation method for attitude control angles of the FSM was proposed. The light path of the output laser of the tracking turntable and the operating principle of the FSM were introduced. Then, the directions of the incident light and emergent light were determined in different coordinate systems and the functional relationship between the attitude control angles and the tracking errors was derived based on the coordinate transformation theory and the reflection law of light. Furthermore, the analytical expressions of the attitude control angles were obtained, and the space distribution characteristics of the attitude angle were explained. A set of approximation expressions of the attitude control angles were derived from the analytical expressions, and the extra pointing errors caused by the approximation expressions were studied. Finally, a pointing precision experiment was performed to verify the correctness of the formulas for calculating the attitude control angles. The experimental results show that both the analytical formulas and the approximation formulas guarantee the pointing error to be less than 2.5″with the turntable tracking errors less than (A12.9′,E13.5′) .However, the approximation formulas cause the pointing errors to grow to 13.2″ and the turntable tracking errors to grow to (A38.6′,E37.8′)while the analytical formulas keep the pointing errors to be within 2.5″. It demonstrates that as terse-form analytical formulas of the attitude control angles have no principle errors, it always can output the laser beam with high precision pointing ability under any turntable tracking errors, and they show simple forms and satisfy the requirement of rapid calculation of servo controllers. fast steering mirror; tracking turntable; pointing accuracy; attitude angle; analytic expression 2016-02-01; 2016-03-07. 吉林省自然科学基金资助项目(No.201115123);国家863高技术研究发展计划资助项目(No.2011AA7031024G) 1004-924X(2016)08-2000-10 TH703; TN249 A 10.3788/OPE.20162408.2000

4 实 验




5 结 论



