多旋翼无人机在变控制量下的三轴磁罗盘校正

徐东甫，白　越, 宫　勋，吴子毅,续志军

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033;

2.中国科学院大学，北京 100039)



多旋翼无人机在变控制量下的三轴磁罗盘校正

徐东甫1,2，白越1*, 宫勋1，吴子毅1,2,续志军1

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033;

2.中国科学院大学，北京 100039)

为了在特殊环境下有效使用多旋翼无人机飞行器的磁罗盘，研究了大电流、控制量变化情况下磁罗盘的校正问题，提出了一种磁罗盘自适应校准方法。推导了磁罗盘误差的变化规律并建立了误差模型，分析了硬磁误差随控制量变化的规律，进而提出了一种基于整体最小二乘法的空间直线拟合方法。通过空间直线拟合，将得到的控制量和硬磁补偿的对应关系用于实时调整对空间飞行器的硬磁补偿，最终解决了控制量变化对磁罗盘的影响。进行了实验验证，结果表明：提出的方法可将飞行器控制量变化带来的磁罗盘硬磁误差基本抵消；在实际飞行中，多旋翼无人飞行器的偏航误差可由最大的15°减小到3°以内。本文所给出的方法在控制量变化，大电流情况下使用时，可以很好地校正磁罗盘航向角误差，提高导航精度。

多旋翼无人机；磁罗盘；变控制量；硬磁误差；误差补偿

*Correspondingauthor,E-mail:baiy@ciomp.ac.cn

1　引　言

近年来，随着无人飞行器技术的成熟[1-3],多旋翼飞行器因其结构简单、操作灵活、具有垂直起降和悬停能力等优点成为了研究热点[4-6]。对于多旋翼飞行器自主飞行，航向角精度和航向角稳定性对其导航非常重要。电子磁罗盘具有体积小、成本低、无累计误差、可自动寻北等特点,被广泛应用于飞行器、车辆的导航系统中，为其提供航向角。但其精度容易受到周围电源、导线、电机等铁磁物质的影响, 因此其校准技术成为研究的热点[7-9]。

文献[10]提出了一种新的标定方法，得到更好的校正效果；文献[11]采用一种避免竖立载体来校正磁罗盘的方法，节省了校正时间；文献[12]利用惯性测量传感器和GPS辅助校正磁罗盘文；文献[13]利用飞行器左右盘旋飞行时的采样数据，实现对载体上铁磁材料引起的罗差的自动补偿，采用椭圆假设算法，利用飞机在多于5个不同方向平飞时的采样数据来自动补偿平飞时的罗差；文献[14]利用多传感器信息，将磁罗盘磁传感器与GPS 或惯性仪表的输出信息进行补偿滤波, 以校准磁传感器的测量值, 具有在线实时补偿能力；文献[15]通过对系数矩阵的奇异性进行分析, 采用最小二乘方法实现了对椭圆模型误差系数的辨识，克服了不稳定性, 对校准过程中的突变干扰有很强的抑制能力。

本文针对多旋翼无人飞行器布局紧凑，磁场环境恶劣、电磁干扰不确定等情况，深入分析磁罗盘的变化趋势，提出了针对控制量变化的磁罗盘自适应校准方法。可有效抵消多旋翼飞行器控制量变化对磁场的影响，对变化的硬磁误差进行补偿，实现不同控制量下的磁罗盘自适应校正。并通过实验，对所提出的校正方法与传统的椭球拟合法在适应范围和精度两方面进行比较, 结果证明了该方法的有效性。

2　磁罗盘误差分析

2.1磁罗盘误差分析

(1)

其中:η=[φ，θ，ψ]T，

图1　参考坐标系Fig.1　Reference coordinate system

进而得到航向角:

(2)

其中:ε为地磁偏角。

三轴磁罗盘的误差分为自身误差和罗差，磁罗盘自身存在的误差包括制造误差与安装误差，这种误差比较固定，可以得到较好的解决。罗差是由磁阻传感器周围的铁磁材料、电器设备等环境磁场与地球磁场混叠产生。因为罗差的存在，使三轴磁罗盘不能正确感应地球磁场，从而产生航向角误差。所以罗差是影响磁罗盘精度最主要的因素。

罗差分为硬磁误差和软磁误差，其误差模型可以由Poisson方程描述:

(3)

磁罗盘在小地域内做任意姿态运动时，地磁场矢量的标量值‖H‖为固定值，若不考虑外磁干扰, 则三轴磁传感器的测量值H满足：

HT·H=‖H‖2,

(4)

取D的2范数并整理为曲面的二次型形式:

(5)

可以认为磁罗盘三轴之间基本正交，不平行角度和感应磁场轴间干扰都较小，所以误差K矩阵严格对角占优，能够保证式中KKT严格对角占优，为正定矩阵。因此式表示一个椭球面。在已知罗差系数且测得H1的情况下, 可以求出H。

H=K-1(H1-σ).

(6)

2.2变控制量时硬磁误差变化

上述校正方法在多旋翼飞行器的控制量不变时是可行的。但如果多旋翼飞行器处在飞行状态下，控制量变化就会产生较强的磁场干扰，影响航向角的精度，该情况在带载能力较强的多旋翼飞行器上表现的尤为严重。主要原因是其执行机构工作电流大、磁场干扰严重，在大地坐标系垂直方向上机动或者更换载荷等情况下，常导致工作电流10 A量级的变化，磁罗盘硬磁误差不断变化，从而导致航向角的偏差。

(7)

当地磁倾角为σ，根据地磁倾角的定义有：

(8)

将式(8)代入式(7)得到罗差:

(9)

由控制量变化在机体坐标系上产生的总磁场矢量Hm大小改变而方向基本不变的。设该磁场强度为Hm，其与XY平面夹角为α，X轴夹角为与Y轴夹角为β。所以电气元件在机体坐标系下的磁场分量为

(10)

将式(10)和(7)带入式(9)：

(11)

在理想的情况下Δφ正比于Hm，又因为Hm随着控制量变化而变化，即在姿态角不变的情况下，罗差(主要是硬磁误差)随控制量变化而变化。

3　磁罗盘自适应补偿算法

由于罗差不恒定，通常的椭球拟合的方法不能满足变化控制量的使用要求。为补偿随着控制量变化带来的硬磁误差，采用整体最小二乘法进行离线拟合，并和传统的椭圆拟合方法相结合，设计了磁罗盘自适应校正算法，如图2所示。

图2　偏航角补偿算法Fig.2　Compensation algorithm of yaw angle

对磁罗盘的补偿分为地面校正和空中校正两部分。在地面时，通过椭球拟合，对磁罗盘进行经典硬磁校正和软磁校正，完成电子磁罗盘的初步校正；同时通过整体最小二乘法进行离线的空间直线拟合，找到控制量与磁场变化量的对应关系；在空中时，主控芯片得到飞行器的控制量，通过控制量与磁场变化量的关系，实时的调整磁场补偿量，抵消因控制量变化带来的磁场影响，得到准确的磁罗盘数据，最后与陀螺仪数据一起经算法融合，得到最终的航向角。

地面校正为：

(11)

同时，针对硬磁误差变化的现象和数据，离线拟合出控制量和磁场的关系，为空中的自适应磁场校正做准备。在工程中，通常使用最小二乘法对大量数据进行拟合，但是在拟合控制量和磁场的关系时存在两个重要问题：

1) 空间直线的一般表达式为：

(12)

为具有6个参数的连等式，并不是简单的线性关系，所以最小二乘法并不能直接拟合[16]；

2)对磁场的测量值本身存在测量误差，普通最小二乘法拟合效果不佳。

针对以上问题，首先将标准型方程转换为整体最小二乘法模型，并用TLS法对数据进行空间直线拟合[18]。

式(12)等价为：

(13)

式(13)化简为：

V=B·ξ-L,

(14)

将式(5)代入平差准则：

对矩阵和参数向量中的各个元素求导,得到迭代方程：

(15)

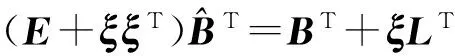
(16)

迭代的具体解算步骤可概括为：

1)获取未知参数的初值ξ(0)；

4)重复步骤2)、3)，直到2次计算的参数值之差小于一定的阈值，退出迭代，输出结果。

4　测量实验与结果

根据现有的实验条件，将首先对不同控制量下多旋翼飞行器进行空间磁场采样实验，并进行椭球拟合，以验证不同控制量对罗差的影响；再通过空间直线拟合算法，离线拟合出控制量和硬磁误差变化量的关系曲线，进而得到准确的偏航数据；最后进行罗差补偿精度对比实验和自主飞行轨迹对比实验，来验证研究内容的实际应用效果。

4.1飞行器磁场采样

为验证式(10)，保持多旋翼飞行器各个执行机构的控制量不变，通过转台分别在X-Y、Y-Z、X-Z平面旋转多旋翼飞行器，对圆周上的各点磁场强度采样记录，进行椭球拟合。然后增加控制量，重复上述试验过程，最终得到多旋翼飞行器在不同控制量时的磁场采样拟合曲线，如图3所示。

图3　磁罗盘采样拟合Fig.3　Sample fitting of Magnetic compass

图4　空间最小二乘法拟合曲线Fig.4　Total least square fitting of space line

可见飞行器的执行单元和导线等电气元件，在机体坐标系上产生了一个大小随控制量增大而增大的磁场分量，且其变化方向在空间内基本保持一条直线，这在本质上是硬磁误差的变化，因此实验结果符合上文结论：随着控制量的变化，飞行器的硬磁误差也随之变化。

为补偿这部分变化的硬磁误差，使用整体最小二乘法，在离线情况下，通过已有的飞行器磁场采样数据，拟合各个椭球心的连线即得到了控制量和磁场变化量的关系，如图4所示。

通过整体最小二乘法离线拟合出控制量与磁场变化量的关系，实时的调整磁场补偿量，抵消因控制量变化量的磁场影响，得到准确的磁罗盘数据，最后与陀螺仪数据一起经算法[17]融合，得到准确的航向角。

4.2罗差补偿精度对比试验和实际使用对比

将无人飞行器固定在无磁转台上，然后转台上以间隔旋转一周，分别用传统的椭球拟合法和本文的方法对磁罗盘进行罗差补偿，通过对比飞行器处在静止、起飞和加速3种状态下的磁航向角剩余误差Δψ。如图5～7所示，飞机的控制量分别为0、200和300(对应电流为0 A、32 A、53 A)，φ1为校正前的磁航向角剩余误差，φ2为只进行传统椭圆拟合校正后的磁航向角误差，φ3为进行本文方法校正后的磁航向角剩余误差。

图5　磁航向剩余误差(0控制量电流0 A时)Fig.5　Residual error of Magnetic heading (controlled quantity at 0)

图6　磁航向剩余误差(200控制量电流32 A时)Fig.6　Residual error of Magnetic heading (controlled quantity at 200)

图7　磁航向剩余误差(300控制量电流53 A时)Fig.7　Residual error of Magnetic heading (controlled quantity at 300)

图5～7的结果统计如表1所示，在静止(控制量为0)情况下，磁罗盘自适应校正方法和传统的椭圆拟合方法效果相似，当控制量变化，飞行器在大电流状态下工作时，普通的椭圆拟合罗差校正已不能较好地校正硬磁误差的偏移，而磁罗盘校正方法可以较好的解决此问题；当控制量加大时，两者的校正效果差距进一步加大。

表1　实验结果对比

为进一步验证实验结论，进行多旋翼无人机自主轨迹飞行对比试验。使用本文方法校正磁罗盘和传统校正方法进行自主飞行，图8所示为使用传统校正的飞行轨迹，图9所示为使用本文自适应校正的飞行轨迹。

图8　传统校正的飞行轨迹Fig.8　Flight path before correction

图9　自适应校正的飞行轨迹Fig.9　Flight path after correction

使用本文校正方法后，自主飞行的误差明显减少，可见本方法对控制量变化引起的磁航向角误差有较好的校正效果。

5　结　论

多旋翼无人飞行器磁罗盘的误差会随控制量变化而变化，具体表现为硬磁误差的偏移。当飞行器工作在大电流，控制量变化的环境时，普通的罗差补偿方法无法很好的完成校正工作。本文首先通过整体最小二乘法拟合得出了飞行器控制量变化和磁场的变化关系；然后结合经典罗差补偿，对飞行器进行地面和空中两种校正。经实验证明，此方法确实有效：将飞行器控制量变化带来的磁罗盘硬磁误差基本抵消，飞行器在空中飞行时磁航向误差减小到3°以内，基本达到了使用要求。另外，对影响磁罗盘精度的多个干扰源一次校正，在野外的工作中减少了大量工作。

[1]李迪，陈向坚，续志军．增益自适应滑模控制器在微型飞行器飞行姿态控制中的应用[J]．光学 精密工程，2013, 21(5): 1183-1191.

LI D, CHENG X J, XU ZH J. Gain adaptive sliding mode controller for flight attitude control of MAV[J].OptPrecisionEng., 2013, 21(5): 1183-1191.

[2]钱默抒, 姜斌, 许德智, 等. 无人机姿控系统鲁棒动态面容错控制设计[J]. 系统工程与电子技术, 2014, 36(9): 1798-1803.

QIU M SH, JIANG B, XU D ZH,etal.. Robust dynamics surface fault tolerant control design for attitude control systems of UAV[J].SystemsEngineeringandElectronics,2014,36(9): 1798-1803.

[3]宫勋，白越，赵常均，等．Hex-Rotor无人飞行器及其飞行控制系统设计[J]．光学 精密工程，2012, 20(11): 2450-2458.

GONG X, BAI Y, ZHAO CH J,etal.. Hex-Rotor aircraft and its autonomous flight control system [J].Opt.PrecisionEng., 2012, 20(11): 2450-2458. (in Chinese)

[4]张欣, 白越, 赵常均, 等. 多旋翼姿态解算中的改进自适应扩展Kalman算法[J].光学 精密工程, 2014, 22(12): 3384-3390.

ZHANG X, BAI Y, ZHAO CH J,etal.. Improved adaptive extended Kalman algorithm for attitude estimation of multi-rotor UAV [J].Opt.PrecisionEng., 2014, 22(12): 3384-3390. (in Chinese)

[5]SEBESTA K D, BOIZOT N. A real-time adaptive high-gain EKF, applied to a quadcopter inertial navigation system [J].IEEETransactionsonIndustrialElectronics, 2014, 61(1): 495-503.

[6]GRZONKA S, GRISETTI G, BURGARD W. A fully autonomous indoor quadrotor[J].Robotics,IEEETransactionson, 2012, 28(1): 90-100.

[7]FANG J, SUN H, CAO J,etal.. A novel calibration method of magnetic compass based on ellipsoid fitting[J].InstrumentationandMeasurement,IEEETransactionson, 2011, 60(6): 2053-2061.

[8]MARKOVIC R, KRAJNC A, MATKO D. Calibration of a solid-state magnetic compass using angular-rate information from low-cost sensors[J].Science,Measurement&Technology,IET, 2011, 5(2): 54-58.

[9]LI M, ROUF V T, THOMPSON M J,etal..Three-axis Lorentz-force magnetic sensor for electronic compass applications[J].MicroelectromechanicalSystems,Journalof,2012, 21(4): 1002-1010.

[10]FARAJIDAVAR A, BLOCK J M, GHOVANLOO M. A comprehensive method for magnetic sensor calibration: A precise system for 3-D tracking of the tongue movements[C].EngineeringinMedicineandBiologySociety(EMBC), 2012AnnualInternationalConferenceoftheIEEE.IEEE, 2012: 1153-1156.

[11]戴磊,齐俊桐,吴冲,等.旋翼飞行机器人磁罗盘误差分析及校准[J].2012, 23(4): 418- 423.

DAI L,QI J T,WU CH,etal.. Magnetic compass error analysis and calibration for rotorcraft flying robot [J].Robot,2012,23(4):418-423.

[12]蔡体菁, 刘莹, 宋军, 等. 嵌入式 GPS/MIMU/磁罗盘组合导航系统[J]. 仪器仪表学报, 2011 (12): 2695-2699.

CAI T J, LIU Y,SONG J,etal.. Embedded integrated GPS/MIMU/compass navigation system[J].ChineseJournalofScientificInstrument,2010,31(12):2695-2699.

[13]刘诗斌. 无人机磁航向测量的自动罗差补偿研究[J]. 航空学报, 2007, 28(2)：411-414.

LIU SH B, Study on automatic magnetic deviation compensation of mafntic heading measurement for UAV [J].ActaAeronauticaetAstronauticaSinica, 2007, 28(2): 411-414.

[14]MARKOVIC R, KRAJNC A, MATKO D. Calibration of a solid-state magnetic compass using angular-rate information from low-cost sensors[J].Science,Measurement&Technology,IET, 2011, 5(2): 54-58.

[15]刘仁浩, 王华. 数字磁罗盘的全姿态罗差补偿[J]. 光学 精密工程, 2011, 19(8): 1867.

LIU R H, WANG H. All attitudemagnetic deviation compensationfor digital magnetic compass [J].Opt.PrecisionEng., 2011, 19(8): 1867.

[16]丁克良, 沈云中, 欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学学报: 自然科学版, 2010 (1): 44-47.

DING K, SHENG Y, OU J K. Methods of line-fitting based on total least-squares [J].JournalofLiaoningTechnicalUniversity(NaturalScience), 2010, 29(1): 44-47.

[17]韩辅君, 徐静, 宋世忠. 基于低成本多传感器的自适应组合滤波[J]. 光学 精密工程, 2011, 19(12): 3007-3015.

HAN F J, XU J, SONG SH ZH. Adaptive attitude estimation filtering with low-cost multi-sensors for MAHRS[J].Opt.PrecisionEng., 2011, 19(12): 3007-3015.

徐东甫(1987-)，男，吉林省吉林市人，博士研究生，2011年于吉林大学获得学士学位，主要从事无人飞行器组合导航与控制方面的研究。E-mail:xu.dong.fu@163.com

导师简介：

续志军(1953-)，男，吉林长春人，研究员，博士生导师，主要从事电子技术、自动控制方面的研究。E-mail：xuzj538@ciomp.ac.cn

(版权所有未经许可不得转载)

Correction of 3-axis magnetic compass in multi-rotor UAV under variable control amounts

XU Dong-fu1,2, BAI Yue1*,GONG Xun1, WU Zi-yi1,2, XU Zhi-jun1

(1.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China； 2.UniversityofChineseAcademyofSciences,Beijing100039,China)

To use effectively the magnetic compass in a multi-rotor Unmanned Aerial Vehicle(UAV) in special environments, this paper researches the magnetic deviation correction method when it works at a large current and a variable control amount. Firstly, the variation patterns of magnetic deviation were derived and an error model was established. The relationship between hard magnetic error and the control amount was also analyzed. Then, a spatial linear fitting method was proposed based on Total Least Square (TLS). Finally, the relationship between hard magnetic error and control amount was adopted to implement the hard magnetic compensation of the UAV. In this way, the magnetic deviation was adaptively compensated and the compass was corrected in real time. Experimental results indicate that the hard magnetic deviation from the changed control amount can be counteracted by proposed method, and the yaw error of the UAV reduces from 15°to less than 3°during the flight. It concludes that the method proposed in this paper effectively corrects the yaw error of the magnetic compass when it works at the high current and large control amount and the navigation accuracy and capability to variable loads of the UAV is improved greatly.

multi-rotor Unmanned Aerial Vehicle(UAV); magnetic compass; variable control amount; hard magnetic error;error compensation

2015-11-12；

2016-01-11.

国家自然科学基金资助项目(No.11372309, No.61304017)；吉林省科技发展计划重点项目(No.20150204074GX)；吉林省与中科院合作科技专项资金资助项目(No. 2014SYHZ0004)

1004-924X(2016)08-1940-08

V279; V241.61

A

10.3788/OPE.20162408.1940