图像椭圆扁度不变性及其在仿射不变量构造中的应用
季 超,杨晓东,王 炜
(海军潜艇学院,山东 青岛 266199)
图像椭圆扁度不变性及其在仿射不变量构造中的应用
季超*,杨晓东,王炜
(海军潜艇学院,山东 青岛 266199)
针对传统基于面积比不变的仿射不变量方法具有的特征点选取不稳定且有冗余以及区域面积误差累积等特点,提出了一种基于图像椭圆扁度划分策略的仿射不变量构造方法。介绍了图像仿射变换模型,得到了图像仿射近似条件。结合图像椭圆扁率定义,依据不变矩理论证明了仿射变换下图像扁率的不变性。给出了图像扁度的定义及其物理含义,并以此作为图像同心圆划分依据,选取三阶以下仿射不变矩作为图像特征量,通过计算各同心圆区域的仿射不变量描述图像目标。将提出的方法应用于实际舰船图像并结合离散系数对其稳定性进行了分析。结果表明:同一舰船目标各种仿射变换图像计算所得扁度相同,所在划分特征圆区域仿射不变量离散系数最大为1.55%。得到的结果显示该方法对目标图像的特征区域划分具有唯一性,构造的仿射不变特征稳定性较好。
图像椭圆扁度;仿射不变量;图像特征;图像识别
*Correspondingauthor,E-mail:jichao200611@163.com
1 引 言
仿射不变量不受形状采集视点变化和相机内外参数的影响,与其它形状特征量相比,在特征稳健性、区分度和适用范围等方面具有很大优势[1]。根据仿射几何理论不变性质知,仿射变换前后两对应封闭区域面积比为常数,此性质被广泛应用于仿射不变量的构造。目前基于面积比不变的仿射不变量构造方法主要分为两类:一是基于特征区域构造面积比不变量;二是基于特征点集构造面积比不变量。
文献[2]通过对二值图像在空间上进行划分,以对象在每个环内的分布为特征,将前景对象面积与背景面积之比作为不变特征描述子,当待识别对象存在一定变形时,该描述符可较好地完成匹配,且具有一定的鲁棒性。文献[3]以物体质心为圆心,利用每个圆内质量(面积)与物体总质量(面积)之比构造特征量,该特征量具有平移、旋转、尺度以及反射不变性。文献[4]先计算图像的协方差矩阵,通过计算该矩阵的特征值和特征向量构造出一组同心椭圆,再利用同心椭圆面积比构造一组仿射不变量。上述基于特征区域构造面积比不变量的方法都是通过选择特殊区域如圆环、同心圆或者同心椭圆作为特征区域,构造闭合区域面积比的,本质上都是利用不变矩理论中的零阶矩比值。
Yang提出了一种凸包仿射不变量构造方法,将相邻点构造的三角形面积比作为仿射不变量[5];Zhang等对图像的纹理基元和仿射变换后图像进行自适应分割,将封闭区域两两组合然后相除,构造面积比值的仿射不变量[6];陈涛等提出了扩展质心概念和仿射区域划分方法,通过一系列扩展质心点序列围成的三角形面积比构造仿射不变量[7]。上述基于特征点集构造面积比不变量的方法存在特征点选取不稳定且有冗余、区域面积误差累积等缺点,从而使得特征量不稳定。
在此基础上,本文提出一种基于图像椭圆扁度划分策略的仿射不变量构造方法,文中从理论上证明了图像椭圆扁率的不变性,给出了图像椭圆扁度的定义及其物理含义,得到了基于图像椭圆扁度的划分策略。该方法对目标图像的特征区域划分具有唯一性,构造的仿射不变特征具有较好的稳定性。
2 仿射变换及其近似条件
相机的成像过程是目标从三维空间到二维平面投影变换的过程,通过对目标成像模型的研究表明[8],当三维目标的深度变化相对于相机距离很小时,所获取形状之间满足仿射变换关系。设图像为f(x,y),则其仿射变换定义为:

(1)
其中(x,y)为图像上任意一点,(xT,yT)为其仿射变换后的对应点。仿射变换包括平移、旋转、缩放及反射变换。
图像经仿射变换后保持不变的量,称为图像的仿射不变量。在仿射几何中,仿射变换前后对应两封闭区域面积比为常数,此性质是仿射不变量构造方法的基础。故寻求特征区域是仿射不变量构造的关键之一。
当用两个不同的相机,从不同的角度和距离获取空间中同一个点的图像时,推导出两幅图像上像素坐标之间的关系。令M为空间中一点,在C1、C2平面的像点分别为m1,m2,如图1所示。

图1 不同视点下图像成像模型Fig.1 Imaging model under different viewpoints
为简化计算,假定世界坐标系与摄像机1的相机坐标系重合,则物点M与其像点m1在世界坐标系和图像像素坐标系中的关系为:

(2)
物点M与其像点m2在世界坐标系和图像像素坐标系中的关系为:
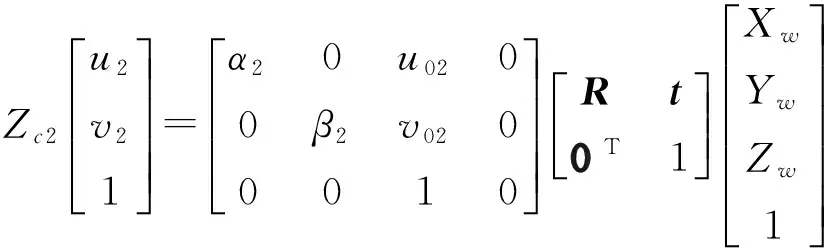
(3)
联立公式(2)和(3),消去世界坐标(Xw,Yw,Zw)T,可得两个像点的像素坐标存在如下关系:

(4)

(5)
[α,β,u0,v0]是相机的内参数,只要相机选定,参数则固定不变,这组参数为绝对不变量。[R t]是相机的外参数,但只要两台相机拍摄的视角和位置固定,参数也固定不变,这组参数为相对不变量。
k1=α2r1+u02r7,k2=α2r2+u02r8,k3=α2r3+u02r9,k4=α2tx+u02tz,k5=β2r4+v02r7,k6=β2r2+v02r8,k7=β2r6+v02r9,k8=β2ty+v02tz。
写成矩阵形式为:

(6)
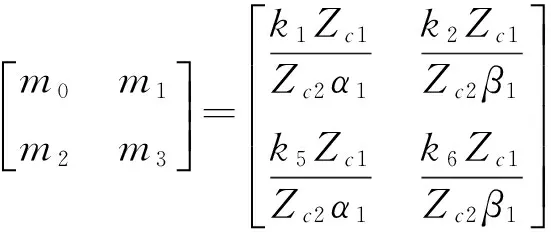
(7)
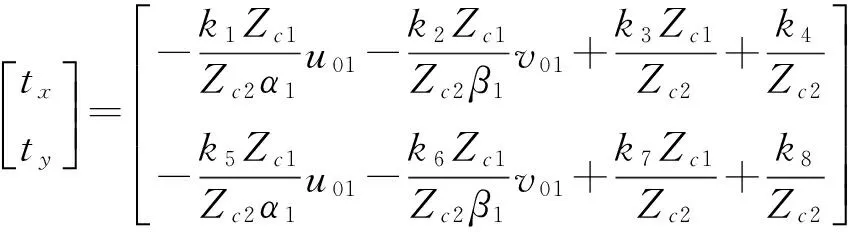
(8)
由式(6)可知,空间中一点的两个像点的图像像素坐标满足仿射变换关系,但对于不同的空间点,Zc1/Zc2不相等,故不同空间点的两个像点坐标所遵守的仿射变换关系不一致,即用两台相机对空间目标进行成像时,所有的像点不能用同一仿射变换模型进行描述。若加入一定的限制条件,使得Zc1/Zc2近似为常量,则该问题便解决。下面为得到的仿射近似的条件:
(1)对于平面目标,若两相机的光轴近似平行,则Zc1/Zc2近似为常数;
(2)对于三维空间中的目标,若目标深度远远小于它与摄像机之间的距离,Zc1/Zc2可以近似为常数;
(3)若目标深度变化不可忽略,对于目标的局部区域,仍可以用同一仿射变换模型来近似。
当摄像机与舰船目标的距离大于舰船深度变化的10倍以上时[8],摄像机获取的舰船图像满足仿射变换条件,本文便是研究仿射变换下图像不变量计算。
3 基于图像椭圆扁度划分策略的仿射不变量
3.1图像椭圆扁率及其不变性证明
记μ20、μ11和μ02表示图像的3个二阶中心矩,则图像经规范化后完全等同于一个具有确定尺寸、方向、离心率,并且中心位于图像质心的辐射度恒定的椭圆,如图2所示,该图像椭圆的两个半长轴p和q记为:
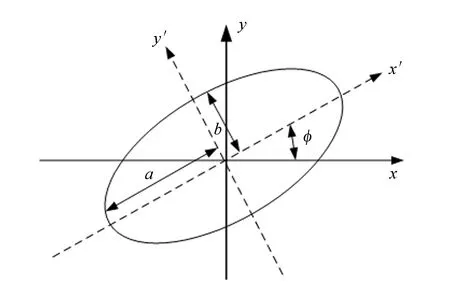
图2 图像椭圆Fig.2 Image ellipse
(9)
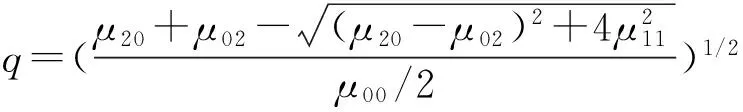
(10)
则扁率E定义为:E=p/q,
(11)
扁率E也称为伸长度(Elongation),它在一定程度上描述了图像区域的紧凑性。当区域为圆时E取得最小值1。
现有基于特征区域构造仿射不变量的方法仅构造一组同心圆或同心圆环,构造规则简单且不具备唯一性,无法体现不同目标图像的差异。本文基于图像椭圆扁率对图像进行划分,能够对图像进行全局和局部描述,构造规则含义明确且具有唯一性,下面给出其不变性证明过程。
证明
图像归一化中心矩ηpq满足
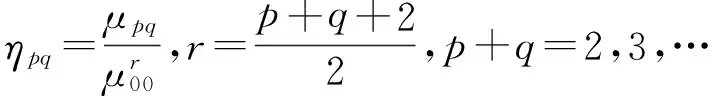
(12)
则由式(12)可得
(13)
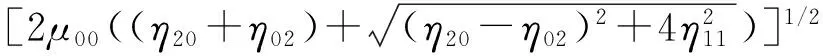
(14)
根据Hu不变矩理论[9]可知
φ1=η20+η02,
(15)

(16)
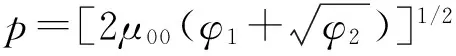
(17)

(18)

(19)
φ1,φ2对于规范化图像为不变量,因此E=p/q为不变量,只要图像经过规范化即可得到不变的扁率E。由于扁率在图像经过规范化后保持不变且唯一,故本文采用其构造特征区域。
3.2基于图像椭圆扁度的特征区域划分
扁率的数值可能不为整数,不能确定构造特征区域具体划分数目,为此本文给出图像椭圆扁度的定义。
扁度:定义 令sc=round(p/q)
(20)
sc称为图像椭圆的扁度,其中round表示取整操作,扁度为图像椭圆扁率取整所得数值,其表示图像形状的紧凑性及圆整度。
以图像f的质心为圆心,选取图像椭圆短半轴长度q为半径,以c1q,c2q,…,cnq(1≤cn≤sc)为半径的一系列同心圆作为特征区域。需要说明的是sc也将作为特征量表征图像。同心圆构造示意图如图3所示。

图3 同心圆构造示意图Fig.3 Diagram of concentric circles construction
3.3图像仿射不变量描述子
Hu矩于1962年提出之后被广泛应用,90年代后期波兰的Flusser给出了二维仿射变换下的不变量,得到4个不变矩用于识别仿射变形的物体[1,8]。然而高阶矩易受噪声干扰、稳健性差。故本文选取三阶以下矩构成的3个仿射不变矩作为仿射不变量。

(21)
3.4算法流程
为了衡量所构造仿射不变量的稳定性,本文采用离散系数来表征数据平均指标。
离散系数又称变异系数,是衡量不同数据集中观测值变异程度的统计量。当两个或者多个数据进行比较时,若度量单位与均值相同,可直接利用标准差比较;若度量单位或均值不同时,则不可以用标准差描述其变异程度,此时需采用标准差与均值的比值来比较,定义为离散系数,其计算公式如下:

(22)


图4 算法流程图Fig.4 Algorithm flow chart
本文算法具体操作步骤如下:
步骤1.图像二值化处理。利用自适应阈值分割方法[10]将目标图像变为二值化图像。
步骤2.图像规范化。为了消除目标图像在各种几何变换下的影响,采用基于协方差矩阵方法将图像规范化[8]。
步骤3.特征区域划分。根据式(19)计算图像椭圆的扁率,求其扁度,根据图像椭圆扁度构造同心圆区域。
步骤4.仿射不变量计算。根据式(21)计算图像各同心圆区域三阶以下的仿射不变量。
4 实验结果与分析
为了验证本文算法的有效性,现以实际拍摄的3类舰船模型图像进行验证。实验中选取的3种舰船分别为171号052C型防空导弹驱逐舰(舰长156 m,宽17.2 m)、999号071型船坞登陆舰(舰长210 m,宽28 m,桅高35 m)、115号051C导弹驱逐舰(舰长155 m,宽17 m)。本实验采用Matlab7.0软件编程实现,操作系统为Windows XP。
实际拍摄过程中,针对每类舰船模型分别设置4种不同距离、4种不同方位角、4种不同俯仰角下共计64张舰船仿射图像,图像像素大小统一为640×480。为了节省篇幅,文中仅给出3类舰船的部分图像,分别如图5~7所示。

图5 171舰船及其仿射变换图像Fig.5 171 ship and its affine transformation images

图6 999舰船及其仿射变换图像Fig.6 999 ship and its affine transformation images

图7 115舰船及其仿射变换图像Fig.7 115 ship and its affine transformation images

图8 文献[3]中仿射不变量Fig.8 Affine invariants proposed by paper [3]

表1 文献[3]中仿射不变量的计算结果及其统计特征
采用文献[3]中的算法构造仿射不变量Ii,1≤i≤n-1,选取n=8,R=1.5,对于1≤i≤8,且ci=0.25i,将计算结果扩大1 000倍,图8(彩图见期刊电子版)给出了3类舰船的7个仿射不变量,其中红色实线代表171舰船不变量数值,黑色实线代表999舰船不变量数值,蓝色实线代表115舰船不变量数值。表1给出了文献[3]中3类舰船不变量计算结果的均值及其统计特征。
根据文献[3]所提算法,由图8及表1可看出:171、115、999三类舰船目标图像均由7个仿射不变量组成;3类舰船目标同一仿射不变量的均值相近,差异较小;三者仿射不变量的离散系数均大于0.80%,其对应的最大离散系数分别为3.89%、2.95%和5.30%。
将实际获取的64张舰船图像利用自适应阈值分割算法将其二值化,采用基于协方差矩阵的方法对其规范化处理,在此基础上,依据式(20)计算图像椭圆扁度,并据此进行特征区域划分,最后依据式(21)计算各图像的仿射不变量。
图8~10(彩图见期刊电子版)给出了3类舰船各图像对应的仿射不变量,图中蓝色实线表示仿射不变量I1,图中黑色实线表示仿射不变量I2,图中红色实线表示仿射不变量I3。
表2~表3分别给出了3类舰船图像对应的仿射不变量及其统计特征。表2~表3中符号说明:Im(n)中m表示式(21)中仿射不变量的下标,n表示扁度sc取值为n时所确定的同心圆区域,即Im(n)表示当sc取n时目标图像在该同心圆区域内计算所得仿射不变量Im。

图9 171舰船仿射不变量Fig.9 Affine invariants of 171 ship

图10 999舰船仿射不变量Fig.10 Affine invariants of 999 ship

图11 115舰船仿射不变量Fig.11 Affine invariants of 115 ship

表2 171 和115舰船各图像仿射不变量统计特征

表3 999舰船各图像仿射不变量统计特征 其中sc=4
依据图9~图11以及表2~表3数据,可得出以下结论:对于同一舰船目标图像而言,即便图像经过了平移、旋转、缩放、倾斜等各种仿射变换,同一舰船目标图像计算所得扁度sc数值相同,即同心圆区域的划分具有唯一性,验证了图像椭圆扁度的不变性;不同舰船图像计算所得sc数值不尽相同,999号sc=4,171与115号sc=3,此数值可反映舰船目标图像的圆整程度,而文献[4]中各舰船目标的不变量数量均为7个,无法体现不同目标图像间的紧凑程度;当sc取值相同时,不同舰船目标图像同一仿射不变量存在差异,如171与115的I2(2)均值分别为220.46、213.94;同一舰船目标图像在不同特征圆区域的同一仿射不变量存在数值差异,可用于表征同一目标图像在不同同心圆区域的差异;171、115与999三类舰船的最大离散系数分别为1.55%、1.42%、1.33%,说明本文所构造仿射不变量的均值稳定性较好,均值稳定性优于文献[3]。
5 结 论
本文提出一种基于图像椭圆扁度划分策略的仿射不变量构造方法。从理论上证明了图像椭圆扁率的不变性,给出了图像椭圆扁度的定义及其物理含义,结合图像椭圆扁度构造同心圆数目存在唯一性特点,选取三阶以下的仿射不变矩作为图像的特征描述子,通过计算同心圆区域的特征量对目标图像进行描述。对3类舰船目标图像的实验结果显示:同一舰船目标其图像椭圆扁度具有唯一性;同一舰船目标图像在所划分特征圆区域的仿射不变量具有较好的稳定性,其最大离散系数为1.55%;不同舰船目标所得扁度不尽相同,可用于表征不同舰船目标的圆整程度。下一步研究重点是考虑所构造特征不变量的分布特性。
[1]FLUSSER J, SUK T. Pattern recognition by affine moment invariants[J].PatternRecognition, 1993,26(1):167-174.
[2]王晓年,邱立可,程宇,等.一种基于环间面积比的旋转、平移和缩放不变性描述符[J].模式识别与人工智能,2012,25(1):82-88.
WANG X N, QIU L K, CHENG Y,etal.. An area ratio between rings based translation, rotation and scale invariant descriptor[J].PatternRecognitionandArtificialIntelligence,2012,25(1):82-88. (in Chinese)
[3]刘亦书.基于协方差矩阵的仿射不变量[J].小型微型计算机系统, 2007,28(7):1282-1286.
LIU Y SH.Affine invariants based on covariance matrix[J].JournalofChineseComputerSystems,2007,28(7):1282-1286. (in Chinese)
[4]刘亦书.一种基于质量(面积)的不变量[J].华南师范大学学报(自然科学版),2007(2):57-61.
LIU Y SH. A set of invariants based on mass/area[J].JournalofSouthChinaNormalUniversity(NaturalScienceEdition) ,2007(2):57-61. (in Chinese)
[5]YANG Z W, COHEN F S. Image registration and object recognition using affine invariants and convex hulls [J].IEEETrans.onImageProcessing, 1999, 8(7): 934-946.
[6]ZHANG J Q, TAN T N. Affine invariant texture analysis based on structural properties[C].Proc.oftheFifthAsianConferenceonComputerVision,Melbourne,Australia, 2002:216-221.
[7]陈涛,粟毅,蒋咏梅,等.利用仿射几何特性提取图像中的仿射不变特征[J].中国图象图形学报,2007,12(9): 1633-1641.
CHEN T, SU Y, JIANG Y M,etal.. Affine invariant feature extraction based on affine geometry[J].JournalofImageandGraphics, 2007,12(9): 1633-1641.
[8]FLUSSER J. Moment invariants in image analysis[C].Proc.ofWorldAcademyofScienceEngineeringandTechnology, 2006,11:196-201.
[9]HU M K. Visual pattern recognition by moment invariants[J].Trans.onInformationTheory,1962,8: 179-187.
[10]HORNG M. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation[J].ExpertSystemswithApplications,2011,38(11):13785-13791.
[11]AVID D, LOWE G. Distinctive image features from scale-invariant keypoints[J].InternationalJournalofComputerVision,2004,60(2):99-114.
[12]RAHTU E, SALO M, HEIKILA J. Affine invariant pattern recognition using multiscale autoconvolution[J].IEEETrans.onPatternAnalysisandMachineIntelligence,2005,27(6):908-918.
[13]王丽,魏巍,吴林钢,等.SAR图像目标识别新方法[J].液晶与显示,2014,29(3):429-434.
WANG L, WEI W, WU L G,etal.. Novel target recognition method for SAR images[J].ChineseJournalofLiquidCrystalsandDisplays, 2014,29(3):429-434.(in Chinese)
[14]李兴唐,曹立华,王思雯.仿射变换的飞行器识别[J].光学 精密工程,2009,17(2):402-408.
LI X T, CAO L H, WANG S W. Aircraft recognition based on affine transform[J].Opt.PrecisionEng., 2009,17(2):402-408.(in Chinese)
[15]MIKOLAJCZYK K.A comparison of affine region detectors[J].InternationalJournalofComputerVision, 2005, 65(1/2):43-72.
[16]孟亚州,马瑜,白冰,等. 基于粒子群优化的Otsu肺组织分割算法[J].液晶与显示,2015,30(6):1000-1007.
MENG Y ZH, MA Y, BAI B,etal.. Improved lung segmentation algorithm based on 2D Otsu optimized by PSO[J].ChineseJournalofLiquidCrystalsandDisplays, 2015,30(6):1000-1007.(in Chinese)
[17]KROLUPPER F, FLUSSER J. Polygonal shape description for recognition of partially occluded objects[J].PatternRecognitionLetters,2007,28:1002-1011.
[18]贾平,徐宁,张叶.基于局部特征提取的目标自定识别[J].光学 精密工程,2013,21(7):1898-1905.
JIA P, XU N, ZHANG Y. Automatic target recognition based on local feature extraction[J].Opt.PrecisionEng., 2013,21(7):1898-1905.(in Chinese)

季超(1987-),男,山东济宁人,博士研究生,2010年于青岛科技大学获得学士学位,2013年于海军潜艇学院获得硕士学位,现为海军潜艇学院载运工具运用工程专业博士研究生,主要从事视觉导航、计算机图像处理与模式识别等方面的研究。E-mail:jichao200611@163.com
导师简介:

杨晓东(1963-),男,山东青岛人,教授,博士生导师,1985年于华东师范大学获得学士学位,2002年于哈尔滨工程大学获得博士学位,现为海军潜艇学院航海教研室主任,主要从事潜艇航行安全技术方面的研究。E-mail:yangxdqtxy@163.com
(版权所有未经许可不得转载)
Invariance of image ellipse oblateness degree and its application to construction of affine invariants
JI Chao*, YANG Xiao-dong, WANG Wei
(NavySubmarineAcademy,Qingdao266199,China)
As the traditional affine invariants based on the invariant of area ratio are characterized by unstable and redundant feature points, error accumulation, this paper proposes a novel method based on the division strategy of image ellipse oblateness degree for construction of affine invariants. The affine transformation model was presented, and the condition of affine approximation was obtained. In combination of the definition of image ellipse oblateness degree and the invariant moment theory, the invariance of image ellipse oblateness under affine transformation was verified. Meanwhile, the definition of image oblateness degree and its physical meaning were given. Then, on the basis of the image ellipse oblateness degree, the affine invariant moments below the 3rd order were selected as the feature descriptors, the image target was described by calculation of the affine invariants of each concentric region. Finally, the proposed method was applied to the actual ship images and its stability was analyzed by discrete coefficients. Experimental results indicate that all kinds of the target images for the same ship under different affine transformations have the same oblateness degree, and the maximum discrete coefficient in the divided feature region is 1.55%.It concludes that the proposed method is unique for the image division and constructed affine invariants have good stability.
image ellipse oblateness degree; affine invariant; image feature; image recognition
2016-05-06;
2016-06-22.
海军装备部“十二五”规划资助项目(No. 435515908)
1004-924X(2016)08-2078-09
TP391.4
A
10.3788/OPE.20162408.2078

