精密行星滚柱丝杠的传动特性

李　凯，叶佩青*，周晓尧，徐　强

(1.清华大学 机械工程系，北京，100010；2.国防科技大学 机电工程与自动化学院，湖南 长沙，410073；3.中国运载火箭技术研究院 第十八研究所，北京，100176)



精密行星滚柱丝杠的传动特性

李凯1，叶佩青1*，周晓尧2，徐强3

(1.清华大学 机械工程系，北京，100010；2.国防科技大学 机电工程与自动化学院，湖南 长沙，410073；3.中国运载火箭技术研究院 第十八研究所，北京，100176)

设计了一种基于行星滚柱丝杠的精密传动机构。根据机电伺服系统的使用要求，分析了行星滚柱丝杠的传动特性。详细阐述了该传动机构的组成、工作原理和主要特点，分析了传动精度和传动效率这两项核心技术指标，得到了各项误差对传动精度的影响程度，如行星滚柱丝杠单向传动误差和回程误差，驱动电机、联轴器、支撑轴承、测量装置和控制系统等的中间装置误差，以及环境因素误差等，推导了传动效率与接触角、螺旋升角的相互关系。最后，构建了实验平台，测试了行星滚柱丝杠的传动精度和传动效率，结果表明其传动精度优于1.5 μm，传动效率优于74%。得到的结果验证了设计的传动机构结构紧凑、承载能力强、传动效率高，传动精度好，在精密传动领域有较大的应用价值。

行星滚柱丝杠；精密传动机构；传动精度；传动效率

*Correspondingauthor,E-mail:yepq@tsinghua.edu.cn

1　引　言

在现代空间探测设备、航空航天武器装备、军事侦察与火控系统、重型超精密数控机床、IC和纳米制造设备等重大国防科技领域，高性能精密传动机构已获得广泛应用，成为决定该类装备性能的核心部件，相关设计制造技术在一定程度上标志着一个国家的科技发展水平[1]。

行星滚柱丝杠(Planetary Roller Screw，PRS)作为一种依靠螺旋运动实现回转运动和直线运动相互转化的机械装置[2]。基于行星滚柱丝杠的精密传动机构，克服了传统液压传动装置固有的“跑、冒、漏、滴”等环境适应性差、可靠性低、使用维护性差等缺点，且综合了行星齿轮传动、谐波齿轮传动、滚珠丝杆、滚针轴承等机构的优点。通过在主丝杠周围布置若干行星螺纹滚柱，大幅增加丝杠传动过程的接触面和受力面，从而具备了“高承载、高效率、高精度、高可靠性”等优点。目前，开展行星滚柱丝杠传动机构研究的技术难点主要体现[2]在：设计制造过程中，长距离传动与高传动精度之间的矛盾；集成设计过程中，负载-驱动-传动-传感-控制的一体化，所导致的高传动精度与高伺服带宽、高控制鲁棒性之间的矛盾。

针对上述情况，本文设计了一种基于行星滚柱丝杠的精密传动机构，阐述了其组成结构、工作原理和主要特点，详细分析了传动效率和传动精度的核心指标，最后通过实验对传动机构特性进行了测试。

2　工作原理

2.1行星滚柱丝杠结构

图1　行星滚柱丝杠结构示意图Fig.1　Schematic diagram of PRS structure

图2　行星滚柱丝杠实物图Fig.2　Photograph of PRS

标准PRS主要由丝杠、滚柱、螺母、直齿、内齿圈、滚柱保持架和弹簧挡圈等组成，如图1和图2所示。

其中，丝杠是牙型角为90°的多头螺纹；滚柱是具有相同牙型角的单头螺纹；螺母是具有与丝杠相同头数和牙型的内螺纹；为了消除丝杠螺旋升角对滚柱产生的倾斜力矩，在滚柱两端加工有直齿，与内齿圈啮合，以确保滚柱轴线平行于丝杠轴线正常滚动；滚柱保持架为确保滚柱沿圆周均匀分布；滚柱保持架由弹簧挡圈轴向定位。其工作原理为：由电机带动旋转的丝杠利用摩擦转矩驱动滚柱转动，继而将丝杠的回转运动转换为螺母的直线往复运动。

与目前广泛应用的滚珠丝杠相比，PRS具有以下优点[3]：承载能力强。滚柱与丝杠接触半径更大，且所有滚柱同时参与啮合成线接触，在相同丝杠直径下，比滚珠丝杠承载能力提高6～15倍；安装空间紧凑。相同负载下比滚珠丝杠节省1/3空间；传动效率高。滚柱丝杠用滚动摩擦代替滑动摩擦，润滑良好的情况下效率可达90%；速度和加速度特性好。丝杠转速可达6 000 r/min，直线速度可达2 m/s以上，加速度可达10 000 rad/s2以上；传动精度高。定位精度优于1 μm；传动噪声低。无需滚动件循环装置，高速运转时产生的振动噪声较小；工作寿命和可靠性高。寿命比同类滚珠丝杠提高10倍以上，可在恶劣工况下可靠工作，无需更换备件；环境适应性强。工作环境温度范围提高2倍以上。

2.2行星滚柱丝杠传动机构组成

采用行星滚柱丝杠传动机构的机电作动器(Electro-Mechanical Actuator，EMA)，主要由编码器、推力轴承、行星滚柱丝杠、电机绕组、缓冲机构和推杆等组成，如图3所示。

此类机电作动器具备以下特点[4]：高承载、高精度与高动态响应等。其承载重量不小于50 000 kg，传动运动范围不小于100 mm，伺服控制带宽30～500 Hz；高功率密度和功能集成度。可实现驱动电机、传动机构、测量装置和控制系统的一体化集成；高可靠性和高使用维护性。在高承载、强过载、大温差、无润滑等非常态工作环境下，具有良好的可靠性和使用性能。

图3　行星滚柱丝杠精密传动机构组成Fig.3　Components of PRS precise transmission mechanism

3　特性分析

传动精度和传动效率作为表征传动机构的核心指标[5-6]，直接影响机构传动效果。

3.1传动精度分析

传动精度通常定义为传动机构实际行程与理论行程之间的偏差[7-12]，即：

(1)

图4　行星滚柱丝杠传动机构误差来源Fig.4　Error sources of PRS transmission mechanism

传动误差主要包括PRS自身误差、中间装置误差和环境因素引起的误差等。通过对传动误差的分析研究，可以从总体上对结构的整个研制过程进行把握和指导13]。

a、PRS自身误差

理论上，PRS传动误差可由丝杠、滚柱和螺母引起的误差进行叠加，但在工程实际中，是不能进行简单线性叠加的，主要误差源如下。

* 导程误差

导程误差可记为ΔP，属于系统误差且为某一固定值。根据传动公式x=Pθ/2π，转换到螺母上的对应位移误差Δxp为：

Δxp=ΔPθ/2π .

(2)

* 力形变误差和弹性接触形变误差

在轴向载荷和扭转力矩作用下，丝杠会发生力形变，形变量与丝杠的支撑方式和有效长度有关，轴向载荷Fa引起的形变误差为δF，扭转力矩M引起的形变误差δM，属于随机误差且服从正态分布，其误差均方根分别为σF和σM。同时，由于滚柱与螺纹滚道面之间仍然是小面积点接触，滚柱与丝杠的弹性接触变形而引起的轴向形变为δS，滚柱与螺母的弹性接触变形而引起的轴向形变为δN，属于随机误差且服从正态分布，其误差均方根分别为σS和σN。总误差可表示为:

Δxd=δF+δM+δS+δN.

(3)

* 同轴度误差

PRS在加工制造过程中，螺纹制造误差造成螺纹与轴颈部的同轴度误差，进而引起传动误差，该项误差为系统误差Δxr且服从周期分布:

(4)

式中:er为螺纹与轴颈部的同轴度误差；dS为丝杠有效直径；θ为丝杠转动角度，P为导程。

* 安装误差

与滚珠丝杠类似，PRS自身径向跳动和轴向窜动也会影响到传动精度。可通过设计预紧螺母等硬件调校机构以减少影响。在精密装配条件下，引起的传动误差Δxa相对较小，属于随机误差且服从正态分布，误差均方根为σa。

* 回程误差

回程误差是指输入轴正向、反向运动一次，实际与理论行程之间的偏差，反映丝杠、滚柱和螺母的螺纹间隙对传动精度的影响，记为Δxh，属于系统误差且为某一固定值。

b、中间装置误差

PRS传动机构是一体化集成装置，除PRS之外，驱动电机、联轴器、支撑轴承、测量装置和控制系统等中间装置也会带来相应误差。

* 驱动电机误差

驱动电机是整个机构的动力源，也是内部振动和热量的主要来源。为了减小电机振动对传动系统的影响，可以将电机安装在隔振材料上；同时，为了避免电机发热，造成局部温升引起形变误差，可以将电机放在恒温罩外。因此，驱动电机引起的误差Δxm相对较小，属于随机误差且服从正态分布，其误差均方根为σm。

* 支撑轴承和联轴器误差

PRS支撑轴承，以及连接电机和PRS的联轴器，在装配过程的轴向偏摆和轴向间隙，会引起丝杠不规则的径向跳动和轴向窜动，进而影响传动精度，以某型推力球轴承为例分析轴承偏心误差和形变误差的影响程度。偏心误差Δxbp是指轴承内圈与丝杠的轴心不重合、轴线不平行，为随机误差且满足正态分布，误差均方根为σbp；形变误差Δxbd是指轴承的接触变形对丝杠传动精度的影响，为随机误差且满足均匀分布，其误差均方根为σbd。

* 测量装置误差

由传动公式x=Pθ/2π可知，通常采用光电编码器等角度传感器对输入角度进行测量，角度测量误差引起的传动误差记为Δxma，即:

Δxma=PΔθ/2π .

(5)

Δxma属于随机误差且服从正态分布，误差均方根为σma。同时，采用直线尺等位移传感器对输出位移进行测量，记为Δxmd，属于随机误差且服从正态分布，误差均方根为σmd。

* 控制系统误差

PRS传动机构作为一种典型的机电伺服控制系统，主要任务是实现对控制指令的精确跟踪。然而，传动系统中存在的间隙、摩擦以及动态负载等非线性影响因素，会对控制系统的指令跟踪精度产生较大影响。控制系统误差记为Δxc，组成相对比较复杂，可视为系统误差和随机误差的复合，分别服从均匀分布和正态分布。

c、环境因素误差

由温度、重力、振动和冲击等环境因素引起的误差属于随机误差，且无法采用精确数学模型加以描述。

对各项误差因素进行综合，代入式(2)～(5)，可得传动误差综合模型:

(6)

式中:Δx为传动误差，右边第一项表征系统误差的综合，K为系统误差项，右边第二项表征随机误差的综合，L为随机误差项。同时，所涉及到的各项误差因素来源、名称、符号、性质和分布，如表1所示。

表1　传动精度的各项误差因素列表

图5　Monte Carlo仿真和灵敏度评估的步骤Fig.5　Procedure of MC simulation and sensitivity assess

为量化分析各项误差因素对传动精度的相对影响程度，采用Monte Carlo仿真方法和灵敏度评价手段[14]对各项误差因素进行统计评估，根据图5所示的步骤和流程，采用各项误差因素的典型值进行仿真。如图6(a)所示为传动误差的三维图，Δx为传动误差，m为仿真样本大小，n为仿真次数；如图6(b)所示为各项误差因素的灵敏度评价直方图，ρ%为权重，xi为各项误差因素。

仿真结果表明：影响传动精度的主要因素为PRS的导程误差和回程误差，以及中间装置的控制系统误差；影响传动精度的次要因素是PRS的力形变和接触形变误差、同轴度误差，以及中间装置的测量装置误差；其他误差因素，如PRS的安装误差、电机误差、测量装置误差和环境因素误差等，影响相对较小。

(a)传动误差三维图(a)3D plot of transmission errors

(b)灵敏度评价直方图(b)Histogram of sensitivity assess图6　Monte Carlo仿真和灵敏度评估结果Fig.6　Results of MC simulation and sensitivity assess

3.2传动效率分析

传动效率通常定义为输出功率与输入功率的比值[15-18]。对于行星滚柱丝杠而言，输入为驱动电机提供的转动力矩，输出为驱动螺母作往复直线运动的推动力，即：

(7)

式中:Wout为输出功率，Win为输入功率；Fa为驱动螺母直线运动的推动力，M为驱动电机的转动力矩；θS为丝杠旋转角度，xN为螺母位移，PS为导程。在理想条件下，忽略行星滚柱丝杠运动过程中的摩擦损耗，则有:

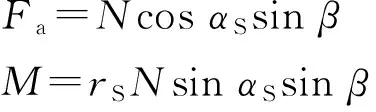
(8)

式中:N为接触点驱动力，αS为丝杠螺旋升角，β为接触角，rS为丝杠螺旋半径。αS、rS和PS之间的关系为:

tanαS=PS/2πrS.

(9)

将式(8)、(9)代入式(7)，可得η=1，即当不存在摩擦损耗时，传动效率可达100%。然而在实际过程中，摩擦对其运动特性具有较大的影响，将接触面滚动摩擦引起的能量损耗记为等效摩擦角ρ，则有:

tanρ=fr/rRPsinβ,

(10)

式中:fr为滚动摩擦系数，fk为滚动摩擦系数，rRP为滚柱面曲率半径。那么，采用等效摩擦角ρ分别对接触面单位公共法向量nC和单位切向向量tC进行修正，可得：

(11)

相应的，驱动螺母直线运动的推动力Fa也就修正为两部分，其一为轴向力FaN，其二为摩擦力Faf，如式(12)和(13)所示。则存在摩擦损耗和相对滑动下传动效率为：

(12)

Fa=FaN+Faf=-N(cosαScosρsinβ-sinαSsinρ-fk(sinαScosρ+cosαSsinρsinβ)),

(13)

(14)

为了分析传动效率与接触角、螺旋升角之间关系，对式(14)进行量化评估，代入某型PRS设计指标参数：rs=0.04 m，fk=0.055，fr=10-5，rRP=0.01 m。同时，设定接触角β取值为0～15°，螺旋升角取值为30～60°，仿真结果如图7所示。

结果表明：接触角β和螺旋升角αS对传动效率η有较大影响。如图7(b)所示，传动效率随接触角增大而增大，最后趋于平稳。当螺旋升角为5～10°时，传动效率趋于稳定时接触角为45°左右。同时，随着螺旋升角的增大，传动效率趋于稳定时的接触角越小。如图7(c)所示，当螺旋升角在10°以内，传动效率随着螺旋升角的增大而增大，而当螺旋升角大于10°时， 传动效率随着螺旋升角增大而减小。同时，传动效率随着接触角的增大其稳定性愈好。

(a)传动效率与接触角、螺旋升角关系三维图(a)3D plot of relationships between transmission efficiency, contact angle and spiral angle

(b)传动效率与接触角、螺旋升角关系二维图(b)2D plot of relationships between transmission efficiency, contact angle and spiral angle

(c)传动效率与接触角、螺旋升角关系二维图(c)2D plot of relationships between transmission efficiency, contact angle and spiral angle图7　传动效率与接触角、螺旋升角的关系Fig.7　Relationships between transmission efficiency, contact angle and spiral angle

4　实验测试

4.1实验平台构建

行星滚柱丝杠传动机构实验平台如图8所示。主要由驱动系统、传动系统、测量系统、控制系统和模拟负载系统等组成。

图8　行星滚柱丝杠传动机构实验测试平台的总体架构和实物照片Fig.8　Structure and photograph of PRS transmission mechanism for experimental test

表2　实验平台设备列表

其中，驱动系统包括Lence MCS 19J30型直流力矩电机和Maxon ADS50/5型PWM脉宽调制功率驱动器；传动系统包括某型行星滚柱丝杠RV21X2的螺母、丝杠、滚柱及其他零配件；测量系统包括Heidenhain RON285-18000型光电编码器、JN338型转速转矩传感器、HK-812型拉力压力传感器和KTC-0150型位移传感器等；控制系统包括接口电路、PC机和dSPACE 1104集成开发平台；模拟负载系统包括静态和动态负载模拟，前者由模拟负载块和NSK公司的超精密直线滚珠导轨平台组成，后者由维杰WEC160型电动缸、FKB-5XN型磁粉制动器、SC-1K张力控制器和控制电源组成。

4.2传动精度测试

根据式(1)对某型行星滚柱丝杠RV21X2的传动精度进行测试。在理想条件下，丝杠输入角度与输出位移关系为x=(37.6 mm/20°)θ，如图9(a)中实线所示。

(a)输入角度与输出位移关系(a)Relationships between input angle and output position

(b)输入角度与输出误差关系(b)Relationships between input angle and output error图9　传动精度测试结果Fig.9　Testing results of transmission precision

在实际测试中，输入角度为正弦信号θ=Asin(2πft)，A=20°，f=0.02 Hz，输出位移如图9(a)中虚线所示，传动精度如图9(b)所示，实验结果表明，PRS传动精度优于1.5 μm。

4.3传动效率测试

图10　传动效率测试结果Fig.10　Testing results of transmission efficiency

对某型行星滚柱丝杠RV21X2的传动效率进行测试，将丝杆特性参数代入式(1)可得:

(15)

进行两次测试，实验结果如图10所示，可知其传动效率优于74%。

5　结　论

本文对行星滚柱丝杠的传动精度和传动效率特性进行了分析，得到了各项误差因素对传动精度的影响程度，以及传动效率与接触角、螺旋升角的相互关系。通过构建实验台对某型机构的传动精度和传动效率进行了测试，结果表明传动精度优于1.5 μm，传动效率优于74%。此机构具有结构紧凑、承载能力强、传动效率高和传动精度好等特点，在精密传动领域有较大的应用价值。

[1]王国彪，赖一楠，范大鹏,等. 新型精密传动机构设计与制造综述[J]. 中国机械工程, 2010, 16(21): 87-95.

WANG G B, NAI Y N, FAN D P. Summary of new type precision transmission design and manufacture [J].ChinaMechanicalEngineering. 2010, 16(21): 87-95. (in Chinese)

[2]黄玉平, 李建明, 朱成林. 航天机电伺服系统[M]. 中国电力出版社, 2013.11: 133-170.

HUANG Y P, LI J M, ZHU C L.Aerospaceelectro-mechanicalservosystems[M]. China Electric Power Press, 2013.11: 133-170. (in Chinese)

[3]刘更,马尚君. 行星滚柱丝杠副的新发展及关键技术[J]. 机械传动, 2012, 05(36): 103-106.

LIU G, MA SH J. New development and key technology of planetary roller screw [J].MechanismTransmission, 2012, 05(36):103-106. (in Chinese)

[4]郭宏, 邢伟. 机电作动系统发展[J]. 航空学报, 2007, 3(28):621-627.

GUO H, XING W. Development of electro-mechanical Actuators [J].ACTAAeronauticaetAstronauticaSinica, 2007, 3(28):621-627. (in Chinese)

[5]刘波, 贾继强. 基于圆柱凸轮的同轴变速传动机构[J]. 光学 精密工程, 2012,8(20): 1766-1771.

LIU B, JIA J Q. Coaxial transmission mechanism based on cylindrical cams [J].Opt.PrecisionEng., 2012,8(20):1766-1771. (in Chinese)

[6]黑沫, 鲁亚飞. 基于动力学模型的快速反射镜设计[J]. 光学 精密工程, 2013,1(21): 54-61.

HEI M, LU Y F. Design of fast steering mirror based on dynamic model [J].Opt.PrecisionEng., 2013,1(21): 54-61. (in Chinese)

[7]YOUSEF H. A comprehensive study on capabilities and limitations of roller screw with emphasis on slip tendency [J].MechanismandMachineTheory, 2009, 44:1887-1899.

[8]TSELISHCHEV A S. Elastic elements in roller-screw mechanisms [J].JournalofRussianEngineeringResearch. 2008, 28(11): 104-1040.

[9]SCHINSTOCK D E. Dynamic load testing of roller screw EMAs [C].Proceedingsofthe3lstIntersocietyEnergyConversionEngineeringConference,IECEC,Washington,1996,8:221-226.

[10]KARAM W, MARE J C. Modeling and simulation of mechanical transmission in roller screw electro-mechanical actuators [J].AircraftEngineeringandAerospaceTechnology. 2009, 81(4): 288-298.

[11]王平, 张葆, 程志峰. 变焦距镜头凸轮结构优化设计[J]. 光学 精密工程, 2010, 18(4): 893-898.

WANG P, ZHANG B, CHEN ZH F. Optimal design of cam structure of zoom lens [J].Opt.PrecisionEng., 2010, 18(4): 893-898. (in Chinese)

[12]肖前进, 贾宏光. 电动舵机伺服系统非线性辨识及补偿[J]. 光学 精密工程, 2013,8(21):2039-2047.

XIAO Q J, JIA H G. Identification and compensation of nonlinearity for electromechanical actuator servo system [J].Opt.PrecisionEng., 2013,8(21):2039-2047. (in Chinese)

[13]陈芳. 两级行星滚柱丝杠传动设计与精确度研究[D]. 南京:南京理工大学, 2009: 55-68.

CHEN F.AccuracyresearchandDesignoftwo-stageplanetaryrollerscrew[D]. Nanjing:Nanjing University of Science and Technology, 2009: 55-68. (in Chinese)

[14]周晓尧. 光电探测系统目标定位误差分析与补偿问题研究[D]. 长沙：国防科技大学, 2012.06: 37-67.

ZHOU X Y.Studyonerroranalysisandcorrectionoftargetlocationforelectro-opticaldetectionsystem[D]. Changsha:National University of Defense Technology, 2012.06: 37-67. (in Chinese)

[15]VELINSKY. Kinematics and efficiency analysis of the planetary roller screw mechanism [J].TransactionsoftheASME, 2009.01, 011016-8/131.

[16]VELINSKY. Kinematics of roller migration in the planetary roller screw mechanism [J].TransactionsoftheASME, 2012.06, 061006-6/134.

[17]PIERRE C L. The roller screw: an efficient and reliable mechanical component of electro-mechanical actuators [J].IEEE,1996: 216.

[18]韦振兴. 行星滚柱丝杠副刚度及效率的分析与研究[D]. 武汉：华中科技大学, 2011: 2-8.

WEI Z X.Theanalysisandresearchofstiffnessandefficiencyforplanetaryrollerscrew[D]. Wuhan:Huazhong University of Science & Technology, 2011: 2-8. (in Chinese)

李凯(1983-)，男，山东聊城人，博士研究生,2004年、2006年于国防科技大学分别获学士、硕士学位，主要从事精密传动机构设计与制造，机电系统伺服与控制等方面的研究。E-mail: lktsinghuanudt@163.com

叶佩青(1963-)，男，江苏泰兴人，教授，博士生导师。2005年8月～2009年7月担任精55班班主任，被评为清华大学优秀班主任,主要围绕数控技术和制造装备自动化学术方向开展教学和科学研究工作。E-mail: yepq@tsinghua.edu.cn

(版权所有未经许可不得转载)

Transmission characteristics of precise planetary roller screw

LI Kai1, YE Pei-qing1*, ZHOU Xiao-yao2, XU Qiang3

(1.DepartmentofMachineryEngineering,TsinghuaUniversity,Beijing100010,China； 2.CollegeofMechatronicsandAutomation,NationalUniversityofDefenseTechnology,Changsha410073,China； 3.The18thResearchInstitutionofChinaAcademyofLaunchVehicleTechnology,Beijing100176,China)

A new precision transmission mechanism based on a planetary roller screw was designed. According to the requirements of an electro-mechanical serve system, the transmission characteristics of planetary roller screw were analyzed. The structure constitution, principle and characters of transmission mechanism were demonstrated in detail and the transmission accuracy and transmission efficiency of the precise planetary roller screw were analyzed. Then, the influence factors of different errors on the transmission precision were discussed, such as single-track and return-track errors of the planetary roller screw, errors of intermediate equipment, environment errors, and the relation between transmission efficiency and contact angle, spiral angle was also deduced. Finally, an experiment was established and the kernel characters, the transmission accuracy and transmission efficiency of the precise planetary roller screw were tested. The experimental results show that the transmission precision is superior to 1.5 μm and the transmission efficiency is superior to 74%, which verifies that the designed transmission mechanism has compact construct, powerful load ability, higher transmission efficiency and precision, and good application values in precision transmission fields.

planetary roller screw; precise transmission mechanism; transmission precision; transmission efficiency

2016-01-01；

2016-03-04.

国家自然科学基金重点基金资助项目(No.51135009)

1004-924X(2016)08-1908-09

TH132

A

10.3788/OPE.20162408.1908