基于改进人工蜂群算法的产品拆卸序列规划

宋守许　张文胜　张雷

合肥工业大学，合肥，230009



基于改进人工蜂群算法的产品拆卸序列规划

宋守许张文胜张雷

合肥工业大学，合肥，230009

为了提高复杂产品拆卸序列规划效率，提出了一种改进的人工蜂群算法用于此类问题求解。通过拆卸混合图表达产品零部件之间的连接关系和优先约束关系，并推导出可行拆卸序列的约束表达式，建立拆卸序列规划数学模型和适应度计算公式。对初始种群进行了优先约束规划，提出一种可行度算法用于蜂群对蜜源的搜寻与选择。定义了自适应选择参数、动态平衡可行度与适应度算法的优先配比，以实现复杂产品拆卸序列规划的快速求解。最后以内啮合齿轮泵为实例，利用所提方法进行了拆卸序列规划求解，通过分析实验结果，并对比传统人工蜂群算法，证明了该方法的可行性和高效性。

复杂产品；拆卸序列规划；人工蜂群算法；约束优化

0　引言

拆卸是回收或者维修的重要组成部分[1]，对废旧产品进行拆卸处理能减轻环境污染，促进资源回收利用。拆卸序列规划就是提取产品的结构与装配信息，形成一定顺序的可行拆卸序列，并挑选出符合某种条件的最优拆卸序列。许多学者对其展开了研究。

早期的研究主要倾向于图论研究，如紧固件图[2]、AND/OR图[3]、Petri网[4]等方法。这些方法在一定程度上解决了产品拆卸序列规划中的问题，但随着产品结构的复杂化，拆卸所涉及的零件数量也呈指数增长，传统的拆卸序列规划方法已经无法满足复杂产品的拆卸需求。于是许多学者利用智能进化算法来解决这一问题。张雷等[5]通过人工蜂群(artificial bee colony,ABC)算法对复杂产品拆卸序列进行并行求解。邢宇飞等[6]通过蚁群算法搜索可行解并计算各个解之间的支配关系，得到Pareto解集，从而实现拆卸序列规划。张秀芬等[7]将拆卸混合图模型映射到粒子群模型，通过粒子群算法实现了复杂产品的最优拆卸序列规划。王辉等[8]将拆卸序列规划问题转化为最优路径搜索和寻优解问题，并通过蚁群算法进行求解。吴昊等[9]利用二叉树算法对初始种群的产生、种群的交叉和变异过程进行优化，通过改进的遗传算法实现了拆卸序列规划的求解。

上述研究成果介绍了智能算法在拆卸序列规划求解方面的应用，其中人工蜂群算法相对于其他传统算法有着较好的求解质量[10]，在处理组合优化问题中有着明显的优势。但由于人工蜂群算法[11]是一种新兴算法，在拆卸序列规划方面的应用研究还存在许多不足。故本文根据拆卸序列规划的约束特性，对传统人工蜂群算法中种群的初始化，引领蜂和跟随蜂的活动准则进行了优化，弥补了其在约束判定方面的不足，提高了复杂产品拆卸序列规划的求解效率。

1　拆卸序列规划问题描述

1.1拆卸混合图模型

为了描述产品各个零件之间的连接关系、优先约束关系，本文选择拆卸混合图来表达产品拆卸模型。拆卸混合图[12]描述了各个零件之间的约束关系，由若干节点、无向边和有向边根据一定规则组合而成。

G={V,E,DE}

其中，G代表混合图；V代表节点，表示产品的零件或子装配体，若产品有n个零件，则V={v1,v2,…,vn}；E为无向边；DE为有向边。例如图1某产品拆卸混合图所示，顶点1,2,…,9表示零件或者子装配体，无向边1到2表示零件1与零件2直接存在连接接触关系，有向边1到4表示零件1与零件4存在优先约束关系，且零件1先于零件4拆卸。

图1　拆卸混合图

为了便于拆卸分析，将无向边集合E和有向边集合DE用连接矩阵Gc和优先约束矩阵Gp来表示，Gc对应{V,E},Gp对应{V,DE}。

其中，

i=j时，Cij=0。

i=j时，Pij=0。

于是可以得出图1拆卸混合图的连接矩阵和优先约束矩阵分别为

1.2拆卸序列求解模型

拆卸序列规划实质就是从产品零部件的随机排列组合中，选出一条可行且最优的拆卸序列。

可行拆卸序列要求当前拆卸零件必须具有可拆性。可拆卸零件[13]是指当前零件没有受到其他零件的优先约束，即满足：

(1)

并且，只与其他零件中的一个有连接关系，即满足：

(2)

在拆卸序列中，一个单元拆卸完毕后，需要对连接矩阵和优先约束矩阵进行更新，然后判断下一个单元的可拆性。拆卸序列的可行性通过式(1)、式(2)约束。

同时，在上述可行拆卸序列中，还需要选取最优的拆卸序列。在不同的拆卸序列中，零件与零件之间拆卸方向与拆卸工具是否发生变化也是不同的。为了在可行拆卸序列中寻求拆卸时间最短的序列，需要尽可能少地进行工具与方向的转变。因此，将拆卸方向变化及拆卸工具变化作为拆卸序列最优的判定指标，则有

(3)

式中，T(x)为可行拆卸序列x对应的适应值；k为拆卸序列中第k个零件；s为拆卸序列总的操作次数；ωd为拆卸方向变化权重系数;ωt为拆卸工具变化权重系数。

2　基于改进人工蜂群算法的拆卸序列优化

人工蜂群算法是由土耳其学者Karaboga[14]于2005年提出的一种模拟蜜蜂群寻找优秀蜜源的智能优化算法，也是典型的元启发式算法。人工蜂群算法具有搜索精度高、鲁棒性强和易于操作等特点，在多约束组合优化问题的求解过程中具有明显的优势。而产品的拆卸序列规划从数学本质来说是一个NP困难问题，适合利用人工蜂群算法进行求解。与蚁群算法、粒子群算法和遗传算法相比较，人工蜂群算法的突出优点是在每次迭代过程中都进行全局搜索和局部搜索，能够较大程度地避免陷入局部最优[15]。同时函数优化测试结果[16-17]也表明，人工蜂群算法具有更优异的优化性能。这也是本文选取人工蜂群算法作为求解方法的理由。

2.1初始种群优先约束算法

拆卸序列规划问题是一个具有强约束条件的组合优化问题，在寻优行为之前要满足可行拆卸序列的约束条件。通常情况下初始种群无法充分提取拆卸混合图的信息，故本文提出初始种群优先约束算法，对初始种群进行优先约束规划。

在优先约束算法中，二叉树作为优先约束储存结构，树结构中每个节点最多有两个子树，且有左右、次序之分。当采用中序遍历时，左子树信息在根节点之前读取，右子树信息在根节点之后读取。

在基于零件的二叉树[18]结构中，每个节点代表一个拆卸单元，左子树所代表的拆卸单元总是先于右子树进行拆卸，根节点则介于二者之间。

优先约束矩阵行和表示该行对应的零件在被拆卸前需要优先拆卸的零件个数，作为优先约束算法中的各零件排列顺序的主要判定依据。在优先约束矩阵Gp中，记

(4)

式中，Si为优先约束矩阵行和(以下简称行和)，表示第i行各元素的值之和；pij为不同零件间优先约束关系对应的数值。

定义Sk为零件k的行和；m为与当前零件k存在约束关系的零件集合。则优先约束算法的具体步骤如下。

(1)根据上述定义获取各个零件的优先矩阵行和；令k=1。

(2)判断行和值Sk：①若Sk=-1，则说明该零件已被操作，跳过此零件，k←k+1;②若Sk=0，则说明没有其他零件对此零件k有优先约束关系,令k所在的节点为新的根节点，在根节点的右子节点插入k+1所代表的零件,k←k+1;③若Sk≥1，则利用优先约束矩阵搜索与此零件有优先约束关系的零件集合m。a.当m不存在时，说明对此零件有优先约束关系的零件已被拆卸。令Sk=0，并返回步骤(2)。b.当m存在多个时，令k所在的节点为新的根节点，利用各零件行和Si进行排序，由大到小依次插入根节点的左子节点，每一次插入后令插入零件为新的根节点。并将所有零件m的行和置为-1，避免再次操作。最后，令Sk=0，并返回步骤(2)。

(3)如果k为拆卸序列最后一个零件，则转步骤(4)；否则，返回步骤(2)。

(4)优化完毕，算法结束。

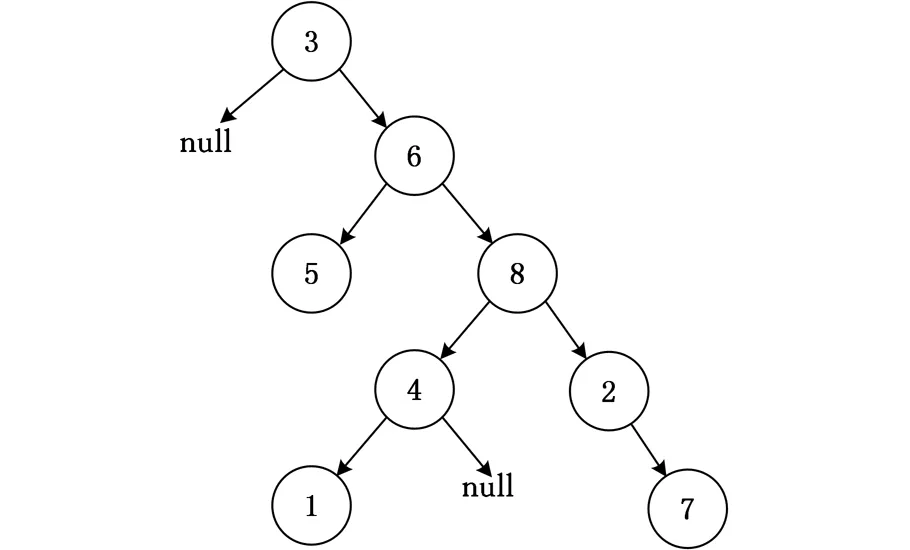
图2　二叉树信息结构

2.2可行度算法与适应度算法

在蜜蜂搜寻和选择蜜源的过程中，提出一种可行度算法，以拆卸序列约束满足程度为基准，指导蜜蜂活动倾向。

一条拆卸序列的约束满足程度取决于拆卸序列可行值与拆卸序列最大维数的比值，则有

(5)

式中，Fx为拆卸序列x的可行度，即表示拆卸序列的约束满足情况；Mx为拆卸序列x可行值，即在拆卸序列中依次连续可拆零件的个数；D为拆卸序列最大维数。

其中拆卸序列可行值M的求解问题可描述为

findXl={X1,X2,…,Xn}

maxg(Xl)

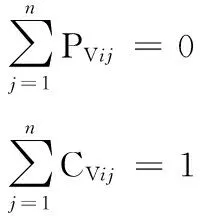
(6)

式中，集合{X1,X2,…,Xl,…Xn}代表一条拆卸序列；Xl为当前拆卸零件；函数g(Xl)为Xl在拆卸序列中的次序；约束条件为可行拆卸序列的约束条件;PVij和CVij分别为可变优先约束矩阵的第i行、第j列元素和可变连接矩阵的第i行、第j列元素。

为了求解该问题，按照拆卸序列次序依次判断当前零件Xl是否具有可拆性，令l=1。如果Xl满足约束条件，则表明当前零件Xl具有可拆性。此时l←l+1，拆卸此零件。当某一零件被拆除时，与之相关的连接关系和优先约束关系也应当去除。反映到可变矩阵上就是：可变连接矩阵CV第i行、第i列所有元素置0，可变优先约束矩阵PV第i列所有元素置0，然后循环此过程，直至所有零件都被拆卸。如果Xl不满足约束条件，则l←l-1，求解结束。取函数g(Xl)的最大值即可获得拆卸序列可行值M。

在引领蜂搜寻蜜源时，由于可行值M之前的元素都已满足约束，只需对其之后元素进行交换即可得到新蜜源；引领蜂通过贪婪准则对新旧蜜源的可行度F进行比较，保留可行度较高者为优秀蜜源；引领蜂将蜜源信息共享于跟随蜂，可行度较高的拆卸序列将吸引更多跟随蜂，其选择概率公式为

(7)

式中，p′x为拆卸序列x的可行度选择概率；NP为种群数量。

相应地，以适应度为依据的蜜源选择算法称之为适应度算法。引领蜂选择蜜源适应度较高者为优秀蜜源，并将信息共享于跟随蜂。跟随蜂根据转移概率公式进行选择：

(8)

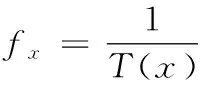
2.3自适应选择算法

可行度算法虽然提高了收敛速度，但新蜜源仅影响可行值M之后的元素，难以保证种群多样性。而适应度算法面向的是拆卸序列中所有元素，在解集多样性的方面优于可行度算法。理想情况下，在算法初期采用可行度算法进行快速约束收敛，中后期逐步采用适应度算法扩大搜索范围和深度，保证种群多样性。本文综合两者优点，定义了一种自适应选择参数：

(9)

式中，H为可行拆卸序列的数量，其值是由种群中满足可行度F=1的拆卸序列个数决定。

自适应选择算法采用轮盘赌的方式决定可行度算法与适应度算法的倾向性。即在区间[0,1]中产生一个均匀分布的随机数r，如果参数α小于r，则采用可行度算法；反之，则采用适应度算法。

算法初期，绝大多数拆卸序列没有满足约束关系，参数α数值较小，可行度算法使用频率居多；随着可行的拆卸序列逐渐增多，参数α逐渐增大，适应度算法会逐步取代可行度算法，以保证种群的多样性。而适应度算法又会降低α的数值，最终二者会在某一范围内实现动态平衡，交替作用于拆卸序列规划的求解。

2.4拆卸序列规划求解流程

至此，可以得出基于改进ABC算法的拆卸序列规划求解流程，如图3所示，步骤如下：

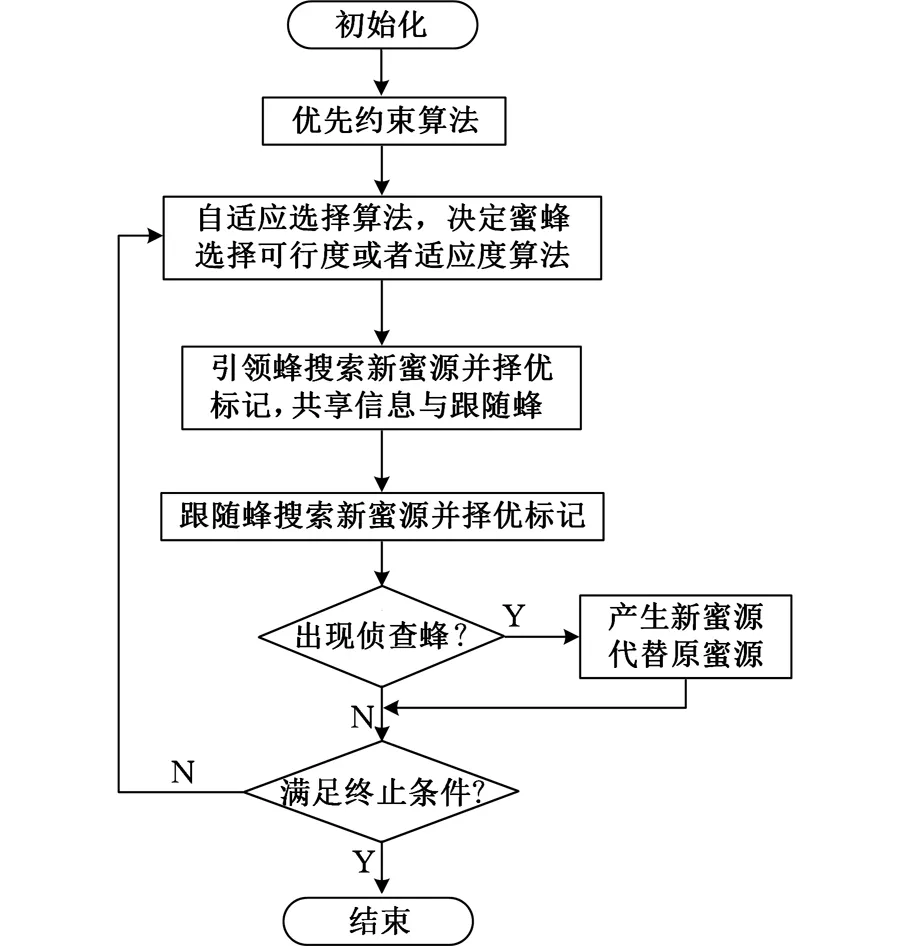
图3　算法流程图

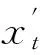
(2)根据2.3节自适应选择算法决定蜜蜂采用可行度算法亦或适应度算法进行计算。

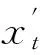
(4)转移概率的计算。在引领蜂搜索结束后，通过摇摆舞的方式将信息与跟随蜂共享，跟随蜂通过式(7)、式(8)计算转移概率并跟随。

(5)跟随蜂搜寻新序列并记录最优序列。当跟随蜂通过转移概率选择序列后，采用与引领蜂一样的方式搜索新序列并记录最优序列。

(6)若通过有限次循环不能被进一步优化，则放弃原序列，侦查蜂根据步骤(1)方法随机生成新序列进行探索。

(7)判断是否满足终止条件，是，则结束循环；否，则返回步骤(2)继续循环。

3　实例分析

基于本文的求解方法，使用MATLAB编写了改进人工蜂群算法程序，并以内啮合齿轮泵为例进行了分析。该模型包括20个最小拆卸单位，其爆炸图见图4，零件信息如表1所示，拆卸混合图见图5。

图4　内啮合齿轮液压泵爆炸图

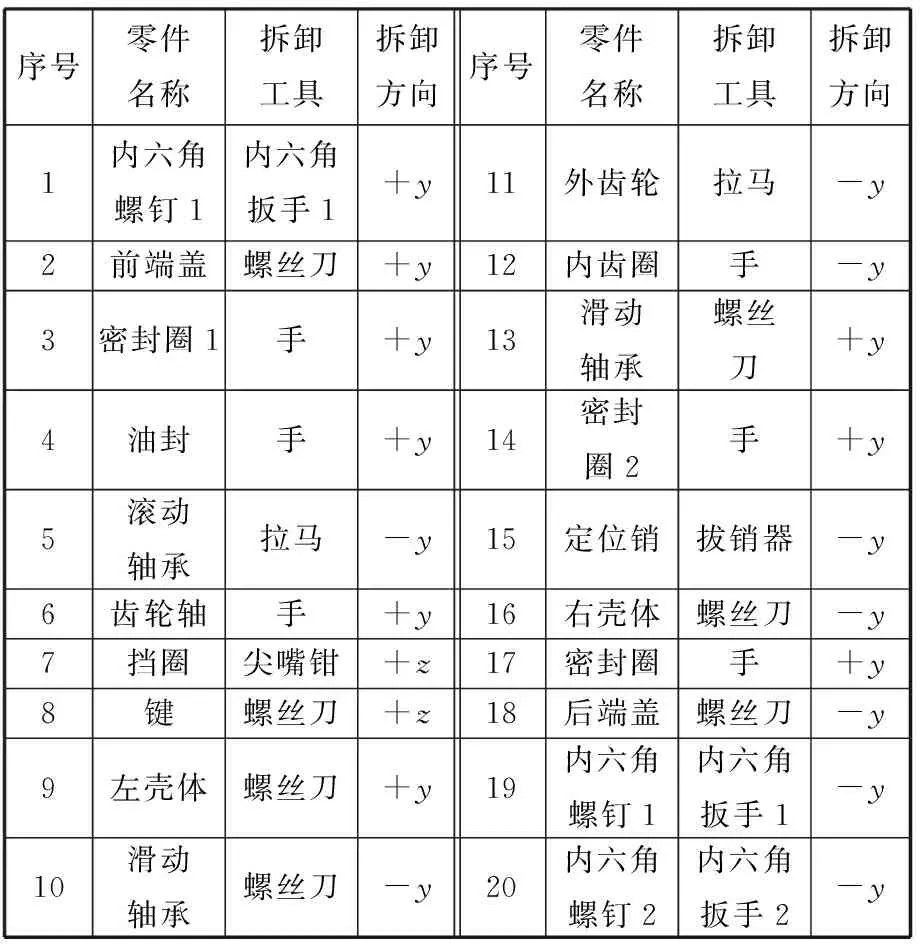
序号零件名称拆卸工具拆卸方向序号零件名称拆卸工具拆卸方向1内六角螺钉1内六角扳手1+y11外齿轮拉马-y2前端盖螺丝刀+y12内齿圈手-y3密封圈1手+y13滑动轴承螺丝刀+y4油封手+y14密封圈2手+y5滚动轴承拉马-y15定位销拔销器-y6齿轮轴手+y16右壳体螺丝刀-y7挡圈尖嘴钳+z17密封圈手+y8键螺丝刀+z18后端盖螺丝刀-y9左壳体螺丝刀+y19内六角螺钉1内六角扳手1-y10滑动轴承螺丝刀-y20内六角螺钉2内六角扳手2-y

改进人工蜂群算法的主要参数设置为：ωd=0.4，ωt=0.6；种群数40，最大循环次数500，单个寻优目标最大循环次数100，经多次反复运算得出最优拆卸序列为1→19→18→20→17→16→15→12→11→8→10→13→2→3→14→4→6→9→7→5，最优适应度为10.4。算法收敛特性如图6所示。在实际拆卸过程中，拆卸工具变化次数为12次，拆卸方向变化次数为8次，经计算T(x)=10.4，与算法计算结果相同，也证明了本算法的可行性。

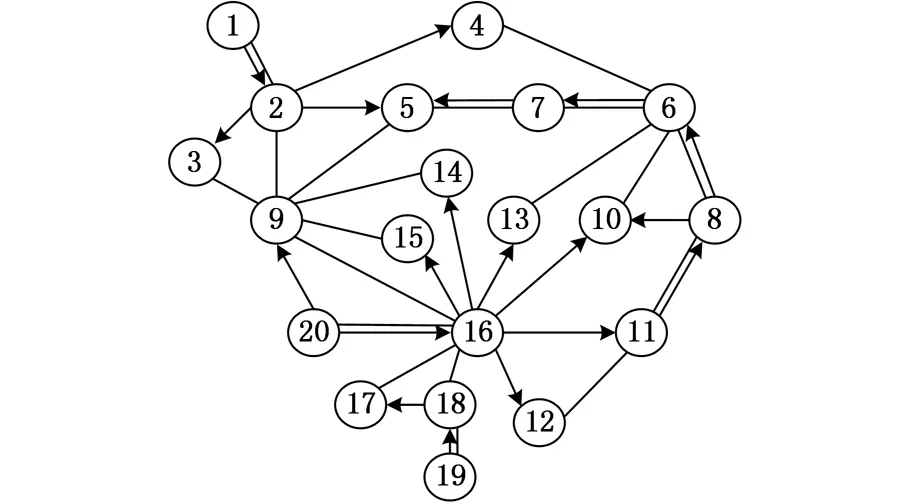
图5　内啮合齿轮液压泵混合图

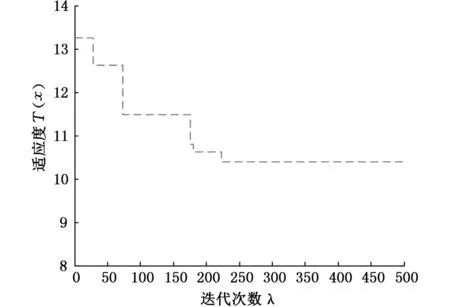
图6　改进ABC算法的收敛特性曲线

为证明本文算法的优越性，将改进ABC算法与文献[5]中传统ABC算法进行比较，以相同参数求解本文实例，得出两种算法的收敛特性曲线，如图7所示。可以看出本文算法的收敛速度和最优结果都优于传统ABC算法。为了避免特定参数的偶然因素，分别以多组参数进行多次实验并取最优数据，结果如表2所示。

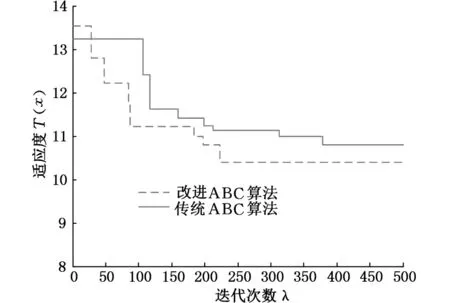
图7　改进ABC算法与传统ABC算法求解实例的收敛特性曲线

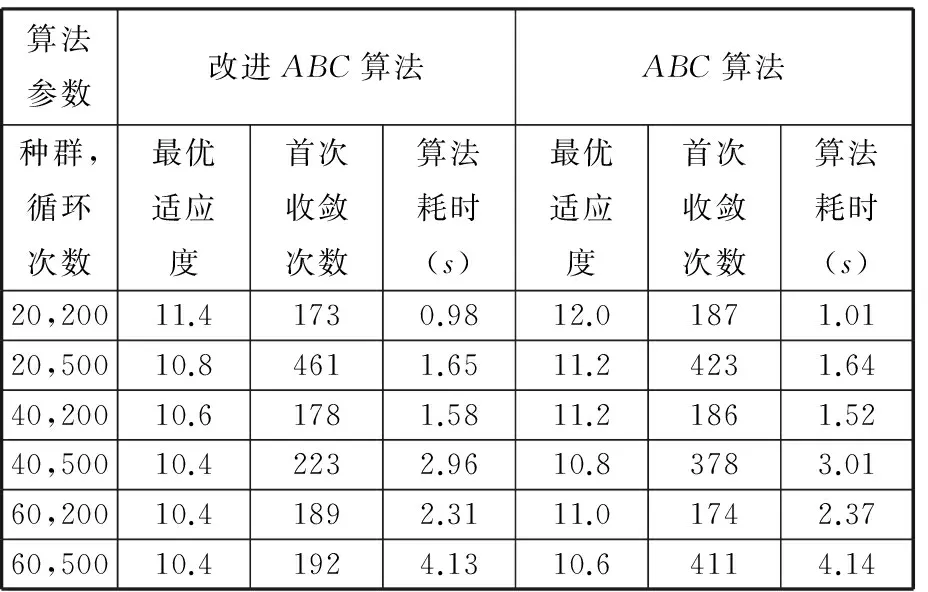
算法参数改进ABC算法ABC算法种群,循环次数最优适应度首次收敛次数算法耗时(s)最优适应度首次收敛次数算法耗时(s)20,20011.41730.9812.01871.0120,50010.84611.6511.24231.6440,20010.61781.5811.21861.5240,50010.42232.9610.83783.0160,20010.41892.3111.01742.3760,50010.41924.1310.64114.14

从表2中数据可知，改进ABC算法在最优适应度和首次达到该适应度的迭代次数上有较大优势，在算法总耗时上与传统ABC算法差距不大。但实际应用中，利用改进ABC算法能够以较少的种群数量和循环次数进行准确求解，从而缩短了求解时间。

将本文算法与文献[7-9]算法进行对比，其中ωd=0.5，ωt=0.5，种群数为40，结果如表3所示。

由表3可知，四种算法均能得到近似最优解，但改进ABC算法更为优异。与蚁群算法相比，改进ABC算法有着较低的迭代次数与较短的运行时间；与粒子群算法相比，改进ABC算法在拆卸方向与工具变化次数方面占据优势；与遗传算法相比，改进ABC算法在运行时间方面有所减少，其余各方面也略有优势。总体来看，改进ABC算法能够利用较少的资源,在较短的时间内，求得较优的解。这主要是由于改进ABC算法在种群初始化阶段能够有效提取混合图信息，同时具有较强的搜索能力，能够根据求解进度自适应调整求解方案，从而降低运算时间，提高求解质量。综上所述，本文提出的改进ABC算法与其他算法相比更具优越性。

4　结论

(1)本文建立了拆卸混合图和拆卸序列规划数学模型，并对拆卸约束特性进分析，指出了传统人工蜂群算法在拆卸序列规划求解方面的问题。

(2)针对随机生成的初始种群无法有效提取拆卸解空间信息的缺点提出了优先约束算法。与同类算法比较，本文算法能够有效避免优先约束关系较低的零件出现在拆卸序列前端导致相关零件搜寻不全面的情况，准确提取优先约束关系。

(3)提出了可行度算法与自适应选择算法，共同指导蜂群活动行为，在保证种群多样性的前提下实现了算法的快速收敛。

(4)实例验证表明，本文所述改进人工蜂群算法具有良好的寻优和收敛性能，能够实现复杂产品拆卸序列规划的快速求解，有助于提高企业拆卸作业的工作效率。

[1]朱兴涛，张则强，朱勋梦，等. 求解多目标拆卸线平衡问题的一种蚁群算法[J]. 中国机械工程, 2014, 25(8): 1075-1079.

ZhuXingtao，ZhangZeqiang，ZhuXunmeng,etal.AnAntColonyOptimizationAlgorithmforMulti-objectiveDisassemblyLineBalancingProblem[J].ChinaMechanicalEngineering, 2014, 25(8):1075-1079.

[2]ZhangH,KuoT.AGraph-basedDisassemblySequencePlanningforEolProductRecycling[J].IEEE/CPMTInternationalElectronicsManufactu-ringTechnologySymposium, 1997(10):140-151.

[3]MooreKE,GüngRAKN,GuptaSM.PetriNetApproachtoDisassemblyProcessPlanningforProductswithComplexand/orPrecedenceRelationships[J].EuropeanJournalofOperationalResear-ch, 2001, 135(2): 428-449.

[4]MeyssamiB.UseofCoagulantsinTreatmentofOliveOilWastewaterModelSolutionsbyInducedAirFlotation[J].BioresourceTechnology, 2005, 96(3): 303-307.

[5]张雷，彭宏伟，卞本阳，等. 复杂产品并行拆解建模及规划方法研究[J]. 中国机械工程, 2014, 25(7): 937-943.

ZhangLei，PengHongwei，BianBenyang,etal.ParallelDisassemblyModelingandPlanningMethodofComplexProducts[J].ChinaMechanicalEngineer-ing, 2014,25(7):937-943.

[6]邢宇飞，王成恩，柳强. 基于Pareto解集蚁群算法的拆卸序列规划[J]. 机械工程学报, 2012,48(9): 186-192.

XingYufei，WangCheng’en，LiuQiang.Disassemb-lySequencePlanningBasedonParetoAntColonyAlgorithm[J].JournalofMechanicalEngineering,2012,48(9):186-192.

[7]张秀芬，张树有. 基于粒子群算法的产品拆卸序列规划方法[J]. 计算机集成制造系统, 2009,15(3): 508-514.

ZhangXiufen，ZhangShuyou.ProductDisassemblySequencePlanningBasedonParticleSwarmOptimizationAlgorithm[J].ComputerIntegratedManufacturingSystems, 2009,15(3):508-514.

[8]王辉，向东，段广洪. 基于蚁群算法的产品拆卸序列规划研究[J]. 计算机集成制造系统, 2006, 12(9): 1431-1437.

WangHui，XiangDong，DuanGuanghong.ProductDisassemblySequencePlanningBasedonAntColonyAlgorithm[J].ComputerIntegratedManufacturingSystems, 2006, 12(9):1431-1437.

[9]吴昊，左洪福. 基于改进遗传算法的产品拆卸序列规划[J]. 中国机械工程, 2009,20(6): 699-703.

WuHao，ZuoHongfu.ProductDisassemblySeque-ncePlanningBasedonImprovedGeneticAlgorithm[J].ChinaMechanicalEngineering,2009,20(6):699-703.

[10]秦全德，程适，李丽，等. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2) : 127-135.

QinQuande，ChengShi，LiLi,etal.ArtificialBeeColonyAlgorithm:aSurvey[J].CAAITransactionsonIntelligentSystems, 2014, 9(2) : 127-135.

[11]KarabogaD,AkayB.AModifiedArtificialBeeColony(ABC)AlgorithmforConstrainedOptimizationProblems[J].AppliedSoftComputing, 2011, 11(3): 3021-3031.

[12]KondoY,DeguchiK,HayashiY,etal.ReversibilityandDisassemblyTimeofPartConnection[J].Resources,ConservationandRecycling, 2003, 38(3): 175-184.

[13]LiJ,KhooL,TorS.ANovelRepresentationSch-emeforDisassemblySequencePlanning[J].InternationalJournalofAdvancedManufacturingTechnology, 2002, 20(8):621-630.

[14]KarabogaD.AnIdeaBasedOnHoneyBeeSwarmforNumericalOptimization[R].Kayseri:ErciyesUniversity. 2005.

[15]张祥银，徐春芳，段海斌. 仿生智能计算[M].北京：北京科学出版社, 2011.

[16]KarabogaD,BasturkB.APowerfulandEfficientAlgorithmforNumericalFunctionOptimization:ArtificialBeeColony(ABC)Algorithm[J].JournalofGlobalOptimization, 2007, 39(3): 459-471.

[17]KarabogaD,AkayB.AComparativeStudyofArtificialBeeColonyAlgorithm[J].AppliedMathematicsandComputation, 2009, 214(1):108-132.

[18]黄星梅，卿海鸽. 基于二叉树的装配体数据[J]. 湖南大学学报(自然科学版), 2003,30(2):47-50.

HuangXingmei，QingHaige.DataStructureofAssemblyModelBasedonBinaryTree[J].JournalofHunanUniversity(NaturalSciences), 2003,30(2):47-50.

(编辑王旻玥)

Product Disassembly Sequence Planning Based on Improved Artificial Bee Colony Algorithm

Song ShouxuZhang WenshengZhang Lei

Hefei University of Technology, Hefei, 230009

To improve the disassembly sequence planning rate of complex products, an improved artificial bee colony algorithm was proposed, which was used to find the answers in the process of disassembly sequence planning. Based on the disassembly hybrid graph model, the connection relationships and disassembly priority relationships were expressed, and the constraint expression of disassembly sequence was obtained. The mathematical model and fitness equation of the disassembly sequence planning were constructed. The initial population was given the priority of constraint algorithm. A feasible algorithm for searching and selecting source nectar was put forward. In order to quickly get the disassembly sequence planning of complex products, an adaptive selection parameter was defined to balance the feasibility and fitness algorithm.Finally, compared with a typical artificial bee colony algorithm, an internal gear pump was studied as an instance to demonstrate the feasibly and efficiency of the method presented.

complex product; disassembly sequence planning; artificial bee colony algorithm; constrained optimization

2015-10-26

国家自然科学基金资助项目(51575152)

TH122

10.3969/j.issn.1004-132X.2016.17.019

宋守许, 男, 1964 年生。合肥工业大学机械与汽车工程学院教授、博士。主要研究方向为绿色设计与绿色制造、废旧产品再资源化理论及技术。发表论文50余篇。张文胜,男,1992年生。合肥工业大学机械与汽车工程学院硕士研究生。张雷,男,1978年生。合肥工业大学机械与汽车工程学院教授、博士。