GA-T-S云推理网络板形模式识别的DSP实现
李海滨 高武杨 来永进 张秀玲
1.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004 2.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004
GA-T-S云推理网络板形模式识别的DSP实现
李海滨1,2高武杨1来永进1张秀玲1,2
1.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004 2.燕山大学国家冷轧板带装备及工艺工程技术研究中心,秦皇岛,066004
针对现有神经网络大多是在软件的基础上进行仿真,训练时间长,不利于工程实际应用的问题,提出了GA-T-S云推理网络板形模式识别的DSP实现方法。首先以设计的板形模式识别GA-T-S云推理网络模型为基础, 利用TI TMS320F2812完成T-S云推理网络的DSP 设计;然后利用MATLAB遗传算法工具箱离线优化T-S云推理网络参数,将优化后的网络参数存入DSP中,进而分别在MATLAB与DSP上运行该网络;最后将运行结果分别进行显示与对比分析。实验结果证实了基于GA-T-S云推理网络的板形模式识别模型有较高的板形识别精度,能够正确识别出板形缺陷的类型,同时验证了GA-T-S云推理网络在硬件TI TMS320F2812上实现的可行性与快速性,从而为神经网络推广应用到实际工程中提供了依据。
T-S云推理网络;板形识别;数字信号处理器;硬件实现;遗传算法
0 引言
近十年来,我国冷轧板带生产需求一直呈现非常旺盛的局面,现代工业的发展对板材的平整度即板形有了更高的要求[1]。板形是板带钢的一个重要质量指标,板形研究的最终目的在于解决板形质量问题。板形模式识别是板形控制的关键环节,其主要任务是根据板形仪检测的板形应力信号,识别出当前带钢中存在的板形缺陷类型,为消除或减小板形缺陷、实现板形控制提供依据。随着人工智能技术的快速发展,许多高效率的算法被应用于板形模式识别。文献[2]提出了一种基于MLSSVR的板形模式识别智能方法,不仅提高了识别的速度和精度,而且具有很强的泛化能力;文献[3-4]引入了万有引力算法,该算法泛化能力强,训练速度快;文献[5]将PID神经网络用于板形模式识别,仿真结果显示PID神经网络能以较高的精度识别出板形缺陷类型;但以上算法识别精度有限,都是进行软件仿真,不能直接用于工程实际。
在概率论和模糊数学的基础上,Li等[6]提出了一种新模型——云模型。黄景春等[7]用正态云模型代替传统模糊集理论中的高斯隶属度函数,结合T-S模糊神经网络,提出了多输入单输出的T-S云推理网络。文献[8]提出了多输入多输出的T-S云推理网络,并用最速下降法辨识网络中的参数。文献[9]设计了基于T-S云推理网络的板形模式识别模型,同时用遗传算法(GA)优化网络中的参数,进而在MATLAB的基础上进行了仿真验证,虽然该模型的识别精度高,能够正确识别出板形缺陷的类型,但这只是软件仿真验证,尚不能直接应用到工程实际。针对该问题,本文在文献[9]的基础上设计了基于DSP的T-S云推理网络,将通过GA离线优化的网络参数存入DSP程序中,并在DSP中运行该网络。实验结果证实了基于GA-T-S云推理网络的板形模式识别模型在硬件DSP上有较高的板形识别精度,能够正确识别出板形缺陷的类型;验证了GA-T-S云推理网络在硬件TITMS320F2812上实现的可行性与快速性,为神经网络更多地应用到实际工程中提供了依据。
1 GA-T-S云推理网络设计
1.1云模型
定义1[10]设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C上的一次随机实现,x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数,即
∀x∈Ux→μ(x)
则x在论域U上的分布称为云,每一个x称为一个云滴。

(1)
则x在论域U上的分布称为正态云。
期望Ex(expectedvalue)、熵En(entropy)和超熵He(hyperentropy)这3个数字特征被用来表征云这个概念。正态云模型以及它的3个数字特征如图1所示。

图1 正态云模型及其3个数字特征
期望Ex代表云滴在论域空间中的分布期望值,可以说是云的最典型样本。熵En一方面是定性概念模糊性的度量,反映论域空间中被概念采纳的云滴数量上的范围;另一方面又是定性概念随机性的度量,反映了可以代表该定性概念的云滴的分散程度。超熵He是熵的不确定性度量,即熵的熵。
1.2T-S云推理网络结构设计
日本学者Takagi和Sugeno于1985年提出了T-S模糊神经网络,该网络由模糊逻辑和神经网络共同构成,具有知识存储、自组织自学习和处理不确定性信息的能力,广泛应用于模式识别和智能控制领域,给模糊控制理论的研究和应用带来了深远的影响。
在T-S模糊神经网络中,经常选择高斯函数作为模糊推理的隶属度函数。高斯函数的表达式为
(2)
高斯隶属度函数的形状和分布如图2所示。在本文中,用正态云模型来取代高斯隶属度函数,云隶属度函数的形状和分布如图3所示。
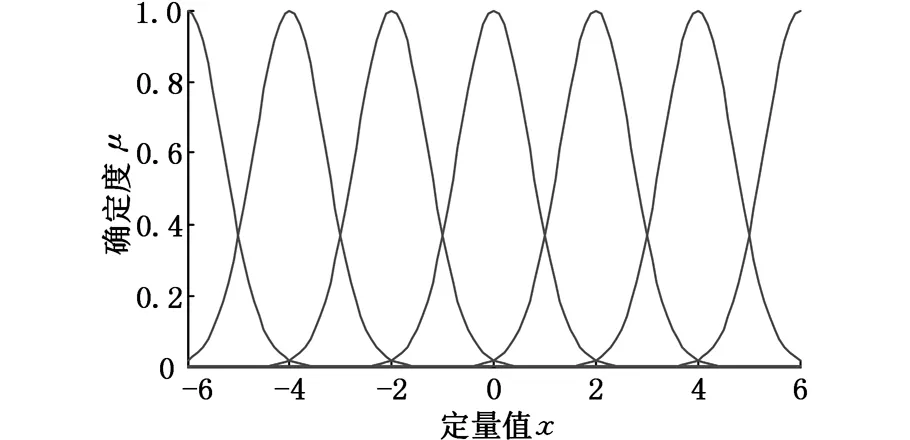
图2 高斯隶属度函数的形状和分布

图3 云隶属度函数的形状和分布

图4 T-S云推理网络结构
由图2和图3可以看出,高斯隶属度函数和云隶属度函数是非常相似的,云模型的引入是为了加强了网络处理不确定性信息的能力,这是因为云模型不仅可以反映模糊性,而且可以描述随机性以及模糊性和随机性之间的关联性。在此基础上,本文设计了T-S云推理神经网络。T-S云推理神经网络的结构如图4所示。前件网络有以下三层。
(1)第一层为输入层,该层是把输入变量引到前件网络,其中节点的数量为n。
(2)第二层为云化层,该层的任一节点都表示一个正态的云模型,作用是把输入变量云化。任一个输入变量的云化划分数为m,总节点数量为mn。
(3)第三层为云推理层,即云规则层。该层的任一个节点代表一条云准则,它的功能是用来配合云规则的前件,计算每条准则的适用度,一般用代数乘积表示(该层的节点数量为m),即
(3)
后件网络层与层之间成线性的关系,算法容易,隐含层的输出为
(4)
x0=1k=1,2,…,rj=1,2,…,m
式中,r为网络输出量的维数。
网络的总输出为
(5)
当第p个样本输入网络中时,误差为网络输出的误差平方之和:
(6)
式中,dk为期望输出。
所有待学习样本输入网络后,总误差E为网络优化的目标函数:
(7)
1.3T-S云推理网络的GA优化
云推理网络的GA优化流程如图5所示。

图5 云推理网络的GA优化流程
GA是模拟自然界中的生物进化过程慢慢演化而来的随机化搜索算法[11],它模拟自然界中选择和生物遗传过程中交叉、变异现象,在迭代的过程中保留一组候选的解,按照某种指标选取比较好的个体,利用遗传算子对这些个体进行重组,产生新的种群,重复上述过程,直至满足指标。
采用GA优化T-S云推理网络,选择式(7)作为适应度函数,选取多个样本来进行网络训练。在超熵He已经确定的条件下,优化前件网络中云模型的数字特征期望Ex、熵En和后件网络中的网络权值w。
2 T-S云推理网络的板形模式识别
2.1板形信号的基本模式
板形识别的目的是根据实际测量到的板形离散信号分辨出当前带钢中存在的板形缺陷类型是由哪一种或几种板形缺陷基本模式以何种组合而来。常见的板形识别信号基本模式包括左边浪、右边浪、中间浪、双边浪、右三分浪、左三分浪、四分浪和边中浪[12],残余应力沿板宽方向的分布曲线如图6所示。

图6 板形基本模式
轧制后带钢板形残余应力值必须满足在板宽横向方向积分值大小为零,即板形性质。基本模式的归一化方程为[13-14]如下。
左边浪的标准归一化方程为
新型职业农民培育工程系统的数据表分析主要包含培训业务、培训业务单位、培训过程和系统监管等信息表的设计。其中,针对培训业务单位的设计内容主要包含工程县编码、村称呼、人口数量、主要行业、主管单位和所属区域等,其中工程县编码为主要工作;针对培训业务的设计内容主要涵盖所有业务编号、名称、日期、人数和参与人员等,其中业务编号为主要工作;针对培训过程的设计内容主要涉及过程编号、时间、授课教师、总人数等,其中过程编号为重点工作;针对系统监管的设计内容主要为用户名称、密码、联系方式以及邮件的主题、发件人、内容和收件人等,其核心工作为用户名称。
(8)
式中, y为带材横向板宽。
右边浪的标准归一化方程为
(9)
中间浪的标准归一化方程为
(10)
双边浪的标准归一化方程为
(11)
右三分浪标准归一化方程为
(12)
左三分浪标准归一化方程为
(13)
四分浪的标准归一化方程为
(14)
边中浪的标准归一化方程为
(15)
轧后板形可表示为板形基本模式的线性组合:
f(y)=a1Y1+a3Y3+a5Y5+a7Y7
(16)
因为ai(i=1,3,5,7)都是可正可负的,所以上述方程实际上表示了8种板形基本模式的线性组合[15]。a1、a3、a5、a7分别代表一次、二次、三次、四次板形偏差的隶属度,其大小代表各次板形偏差的含量,符号表示板形缺陷的类型。
2.2板形模式识别的T-S云推理网络模型结构设计


(17)
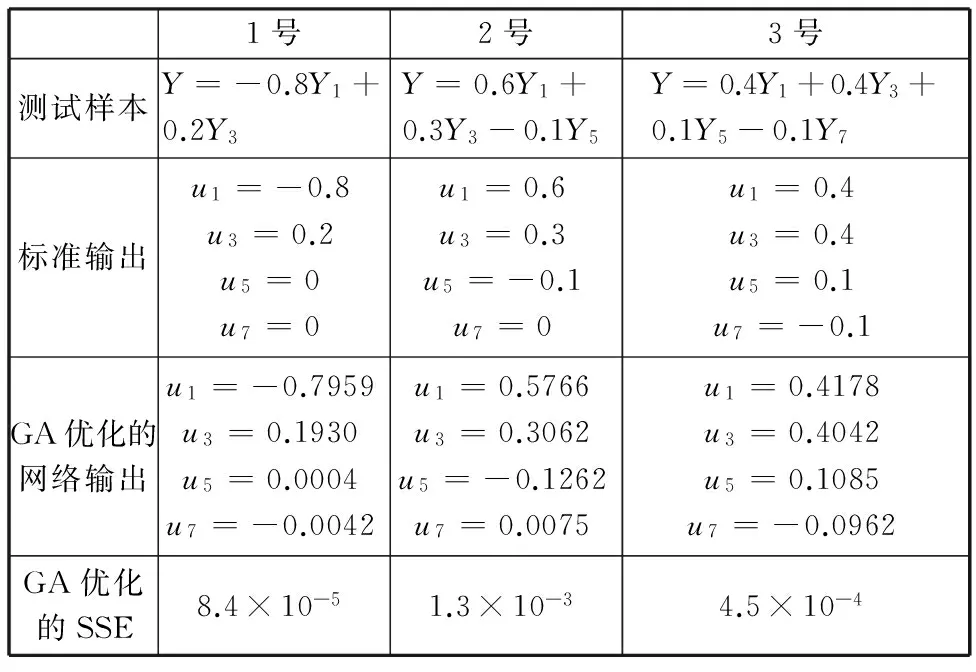
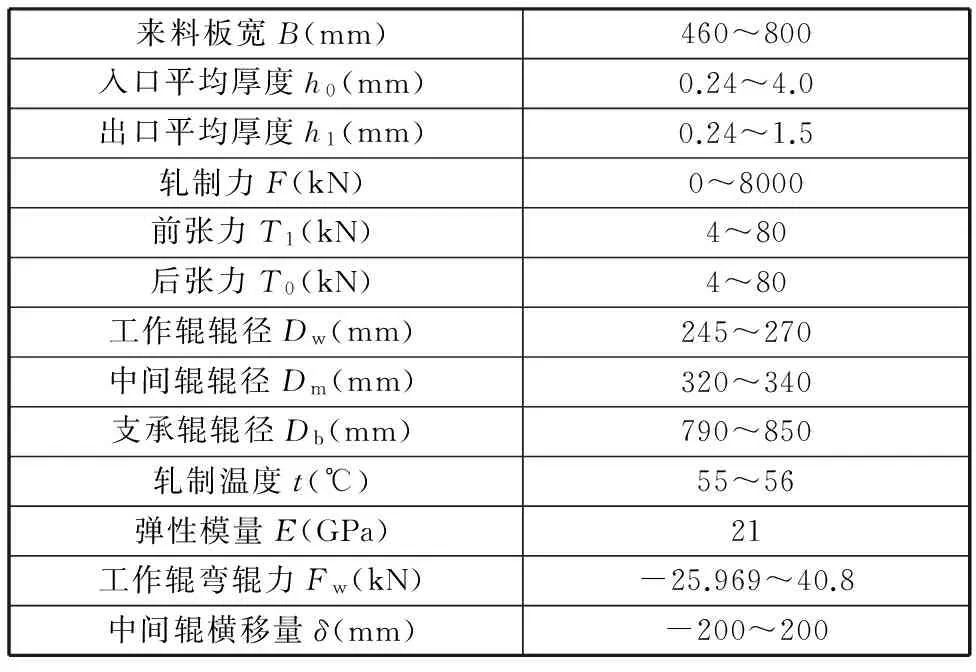
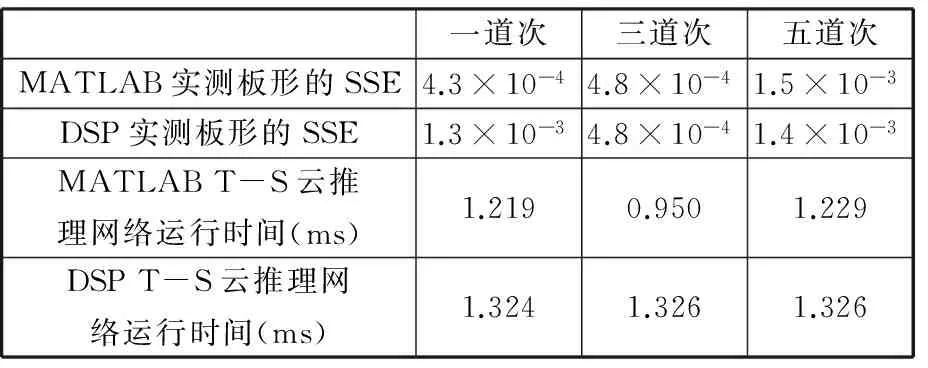
根据轧机执行机构的要求[16],识别出的板形基本模式中不能同时存在左边浪和右边浪、中间浪和双边浪、右三分浪和左三分浪、四分浪和边中浪。设Dk、Dk+1为将要识别的样本和2个互反基本模式之间的欧氏距离,如果Dk 若D1 若D3 若D5 若D7 在确定了板形模式识别的T-S云推理网络模型之后,利用GA优化实现板形识别的T-S云推理网络参数,即前件网络中的期望Ex、熵En和后件网络中的权值,共56个。GA使用实数编码方式,码串个数为56,设置起始种群的大小为20,选择交叉概率为0.8,变异概率为0.2,适应度函数为识别结果与标准输出的误差平方和,如式(7)所示,优化目标为使适应度函数值达到最小。适应度函数的GA优化过程及最佳个体如图7所示。 图7 适应度函数的GA优化过程及最佳个体 网络优化训练完成后,用测试样本来测试其板形识别能力,板形识别结果见表1。其中,SSE表示识别结果与标准输出的误差平方和。 3.1GA-T-S云推理网络DSP实现的背景 人工神经网络具有很强的非线性拟合能力,可映射任意复杂的非线性关系[18],而且学习规则简单,便于计算机实现,具有很强的鲁棒性、记 表1 板形识别结果 忆能力、非线性映射能力以及强大的自学习能力,因此,广泛应用于模式识别、图像识别、智能机器人、预测估计、系统辨识等领域。但神经网络算法至今却较少能够成功应用到实际工程中,分析其原因,主要为以下两点: (1)神经网络的计算量比较大,使用软件编程的方式在基于冯·诺依曼结构的处理器上实现神经网络的功能很难满足工程中实时性的指标要求,同时软件编程的方式只是在进行软件仿真实验,不能将神经网络直接应用到实际工程中。 (2)即使现在芯片生产厂商正努力研制各种针对神经网络的专用芯片,但这些芯片价格较高,同时研制处于初级阶段,到实际应用还需一段时间。 随着微电子技术的蓬勃发展,出现了非冯·诺依曼结构的微处理器,TI公司推出的DSP就是其中的代表产品。DSP一改传统的冯·诺依曼结构,采用了先进的哈佛总线结构[19]。哈佛总线结构的出现使数据的吞吐率高了一倍。DSP的出现使一些由于受传统微处理器速度和结构限制难以实现复杂算法运算速度要求的场合得以实现,且DSP能与外围设备相连,实现对外围设备的控制。 3.2GA-T-S云推理网络板形识别的DSP设计实现 能否有效地将理论成果运用到实际中的一个重要因素就是神经网络的实现问题。关于神经网络的实现以及如何将仿真中得到的网络结构运用到实际控制系统中也有许多方式。这使得神经网络在实际工程中得到广泛的运用。神经网络的实现分为硬件和软件实现两种方式。采用软件方法实现的神经网络算法,其运算速度受计算机主频的限制,同时不能与复杂的外围设备相连,因此,尚不能应用在工程中。而采用硬件方式实现将能有效地加快其运算速度,且硬件能够与外围设备相连,实现对外围设备的控制,故能够应用到实际工程中。 在本文所研究的GA-T-S云推理网络板形模式识别的DSP实现中,选用TI 公司推出的32位定点DSP芯片TMS320F2812。它不仅具有强大的数字信号处理能力,而且具有较为完善的时间管理能力和嵌入式控制功能,被广泛应用于工业控制,特别是应用在处理速度、精度方面要求较高的领域。 在GA-T-S云推理网络的DSP实现中,首先根据T-S云推理网络结构编写基于MATLAB的T-S云推理网络程序,其次利用GA对T-S云推理网络参数进行离线优化辨识,再次根据T-S云推理网络结构编写基于DSP的T-S云推理网络C语言程序,最后将用GA优化好的56个T-S云推理网络参数存入DSP中,运行DSP程序,则该程序能够进行板形识别,GA-T-S云推理网络板形识别的DSP设计与实现流程如图8所示。 图8 GA-T-S云推理网络板形识别的DSP设计与实现流程图 应用DSP实现T-S云推理网络板形识别,其实质就是给设计优化好的T-S云推理网络一个待识别输入信号,对该网络进行推理运算,其主要运用的正是DSP最擅长的乘法和加法运算。 3.3实验结果分析 将GA-T-S云推理板形模式识别模型应用在某900HC六辊可逆冷轧机中,最大轧制力为8000 kN,板带材轧制规格为2.2mm×662mm→0.247mm×662mm,材质为SPHC。轧制参数见表2。采用接触式板形仪,沿板宽方向共有15个测量端,其主要参数B为来料板宽,Bi(i=1,2,…,15)为第i段上板带材的宽度。用板形仪实际测得的数据训练该模型,然后对一、三、五道次的实测板形进行识别。待识别样本见表3。 表2 某900HC六辊可逆冷轧机的轧制参数 表3 待识别的样本 将样本的应力值按式(17)转化为欧氏距离,然后做对应处理,作为板形识别模型的输入。MATLAB实测板形与DSP实测板形识别结果对比见表4。 表4 MATLAB、DSP实测板形识别结果对比 分别将MATLAB程序和DSP程序识别出的板形和实际板形进行对比,相同道次在同一图中,板形曲线如图9所示。 表4和图9表明:基于GA-T-S云推理网络的板形识别模型可以很好地反映出板形缺陷的类型,与实际缺陷类型相比,识别精度较高;该网络在MATLAB与DSP环境下的运行结果相差很小,验证了GA-T-S云推理网络在硬件DSP上实现的可行性;T-S云推理网络在MATLAB与DSP环境下运行时间相差很小,在DSP中运行时间约1.32 ms,能够满足多数实际应用场合(如板形识别)实时性的要求。 图9 MATLAB、DSP一道次板形对比曲线 图10 MATLAB、DSP三道次板形对比曲线 图11 MATLAB、DSP五道次板形对比曲线 (1)基于GA-T-S云推理网络的板形模式识别模型有较高的板形识别精度,能够正确识别出板形缺陷的类型。 (2)通过实验验证了GA-T-S云推理网络在TI TMS320F2812上实时实现的可行性及有效性,说明基于DSP的T-S云推理网络实时实现在板形识别等实际应用领域具有广阔的前景。 (3)MATLAB与DSP有机结合可以充分发挥两者的优点,完成神经网络的优化设计与硬件实现,为神经网络普及推广到实际工程中提供了新方法。 [1]Zhang Yun, Yang Quan, Wang Xiaochen. Control Strategies of Asymmetric Strip Shape in Six-high Cold Rolling Mill [J]. Journal of Iron and Steel Research, International, 2011, 18(9): 27-32. [2]张秀玲,张少宇,赵文保,等.板形模式识别的多输出最小二乘支持向量回归机新方法[J].中国机械工程,2013, 24(2): 258-262. Zhang Xiuling, Zhang Shaoyu, Zhao Wenbao,et al.A Novel Method for Flatness Pattern Recognition via MLSSVR[J]. China Mechanical Engineering, 2013, 24(2): 258-262. [3]牛培峰,李鹏飞,李国强,等.基于万有引力优化的支持向量机模型在板形识别中的应用[J].钢铁,2012,47(12): 45-49. Niu Peifeng, Li Pengfei, Li Guoqiang,et al. Application of GSA-SVR Model in Flatness Pattern Recognition[J].Iron and Steel, 2012, 47(12): 45-49. [4]Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a Gravitational Search Algorithm[J]. Intelligent Information Management, 2012, 4(6):390-395. [5]张秀玲,徐腾,赵亮,等.基于GA-PID神经网络的板形模式识别方法[J].沈阳大学学报(自然科学版), 2013, 25(3): 209-214. Zhang Xiuling, Xu Teng, Zhao Liang,et al. Method of Flatness Pattern Recognition Based on GA-PID Neural Network[J].Journal of Shenyang University(Natural Science Edition),2013, 25(3): 209-214. [6]Li Deyi, Liu Changyu, Liu Luying. Study on the Universality of the Normal Cloud Mode [J]. Engineering Sciences, 2004, 6(8): 18-24. [7]黄景春,肖建,周聪.一种基于T-S云模型的非线性系统的控制[J].电机与控制学报,2009,13(1):149-156. Huang Jingchun, Xiao Jian, Zhou Cong.T-S Cloud Model for Nonlinear Systems Control[J].Electric Machines and Control,2009,13(1):149-156. [8]张秀玲,赵文保,张少宇,等. 基于改进T-S云推理网络的板形模式识别方法[J].中南大学学报(自然科学版), 2013, 44(2): 580-586. Zhang Xiuling, Zhao Wenbao, Zhang Shaoyu,et al. Method of Flatness Pattern Recognition Based on Improved T-S Cloud Inference Network[J].Journal of Zhongnan University(Natural Science Edition), 2013, 44(2): 580-586. [9]Zhang X, Zhao L, Zang J, et al. Hybrid MATLAB and LabVIEW with T-S Cloud Inference Neural Network to Realize a Flatness Intelligent Control System[J]. Steel Research International, 2014, 85(12): 1639-1652. [10]李德毅,杜鹢.不确定性人工智能[M].北京:国防工业出版社,2005. [11]雷英杰. MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2004. [12]单修迎,刘宏民,贾春玉.含有三次板形的新型板形模式识别方法[J].钢铁,2010,45(8):56-60. Shan Xiuying, Liu Hongmin, Jia Chunyu. A Recognition Method of New Flatness Pattern Containing the Cubic Flatness[J]. Iron and Steel,2010,45(8):56-60. [13]张秀玲,刘宏民.板形模式识别的GA-BP模型和改进的最小二乘法[J].钢铁,2003,38(10):29-34. Zhang Xiuling, Liu Hongmin.GA-BP Model of Flatness Pattern Recognition and Improved Least-Squares Method[J]. Iron and Steel,2003,38(10):29-34. [14]何海涛,李楠.基于SVM的改进RBF网络板形模式识别方法[J].自动化仪表,2007,28(5):1-8. He Haitao, Li Nan.The Improved RBF Network Approach to Flatness Pattern Recognition Based on SVM[J]. Process Automation Instrumentation,2007,28(5):1-8. [15]Jung J Y, Im Y T. Simulation of Fuzzy Shape Control for Cold-rolled Strip with Randomly Irregular Strip Shape[J]. Materials Processing Technology,1997,63 (1/3):248-253. [16]Xu Lejiang. Flatness Control in Cold Strip Polling and Mill Type Selection[M].Beijing:Metallurgical Industry Press,2007. [17]Peng Yan, Liu Hongmin, Wang Dongcheng. Simulation of Type Selection for 6-high Cold Tandem Mill Based on Shape Control Ability[J].Journal of Central South University of Technology, 2007, 14(2): 278-284. [18]陈丽安.基于DSP的BP神经网络实时实现[C]//中国自动化学会华东地区第十九届学术年会.青岛,2006:124-126. [19]顾卫钢.手把手教你学DSP——基于TMS320X-281X[M].北京:北京航空航天大学出版社,2011. (编辑陈勇) FlatnessPatternRecognitionviaGA-T-SCloudInferenceNetworkImplementedbyDSP LiHaibin1,2GaoWuyang1LaiYongjin1ZhangXiuling1,2 1.KeyLaboratoryofIndustrialComputerControlEngineeringofHebeiProvince,YanshanUniversity,Qinhuangdao,Hebei,066004 2.NationalEngineeringResearchCenterforEquipmentandTechnologyofColdStripRolling,YanshanUniversity,Qinhuangdao,Hebei,066004 Theexistingneuralnetworkswearemostlysoftwaresimulationandthetrainingtimewaslong,thusthatwouldnotconducivetoengineeringapplications.Inviewoftheaboveproblems,flatnesspatternrecognitionviaGA-T-ScloudinferencenetworkimplementedbyDSPwaspresentedherein.Firstly,theDSP’sdesignofT-ScloudinferencenetworkwasimplementedbyusingTITMS320F2812onthebasisofflatnesspatternrecognitionviaGA-T-Scloudinferencenetwork.ThenT-ScloudinferencenetworkparameterswereoptimizedthroughgeneticalgorithmtoolboxofMATLABinoff-linemannerandtheseparametersweretransmittedtoDSPlater.ThenetworkwasrunonMATLABandDSPseparately.Finally,thetworesultsofT-Scloudinferencenetwork,whichwasrunonMATLABandDSPrespectively,werecomparedandanalyzed.ExperimentalresultsconfirmthatGA-T-Scloudinferencenetworkhavehighaccuracyintermsofflatnesspatternrecognition,itcanidentifythedefecttypesofflatnesscorrectly.Atthesametime,theexperimentalresultsverifythattheT-ScloudinferencenetworkcanrunonthehardwareTITMS320F2812inafastspeedanditprovidesabasisforneuralnetworksappliedtopracticalengineering. T-Scloudinferencenetwork;flatnessrecognition;digitalsignalprocessor(DSP);hardwareimplementation;geneticalgorithm(GA) 2015-10-22 国家自然科学基金资助项目(61007003);河北省自然科学基金-钢铁联合研究基金资助项目(E2015203354);河北省教育厅科学研究计划;河北省高等学校自然科学研究重点项目(ZD2016100) TP273 10.3969/j.issn.1004-132X.2016.17.012 李海滨,男,1978年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为航天测控技术、自主机器人视觉重建、工业过程智能控制。获省级科技进步三等奖1项、仪器仪表科学技术奖1项。发表论文40余篇。高武杨,男,1991年生。燕山大学电气工程学院硕士研究生。来永进,男,1990年生。燕山大学电气工程学院硕士研究生。张秀玲,女,1968年生。燕山大学电气工程学院教授、博士。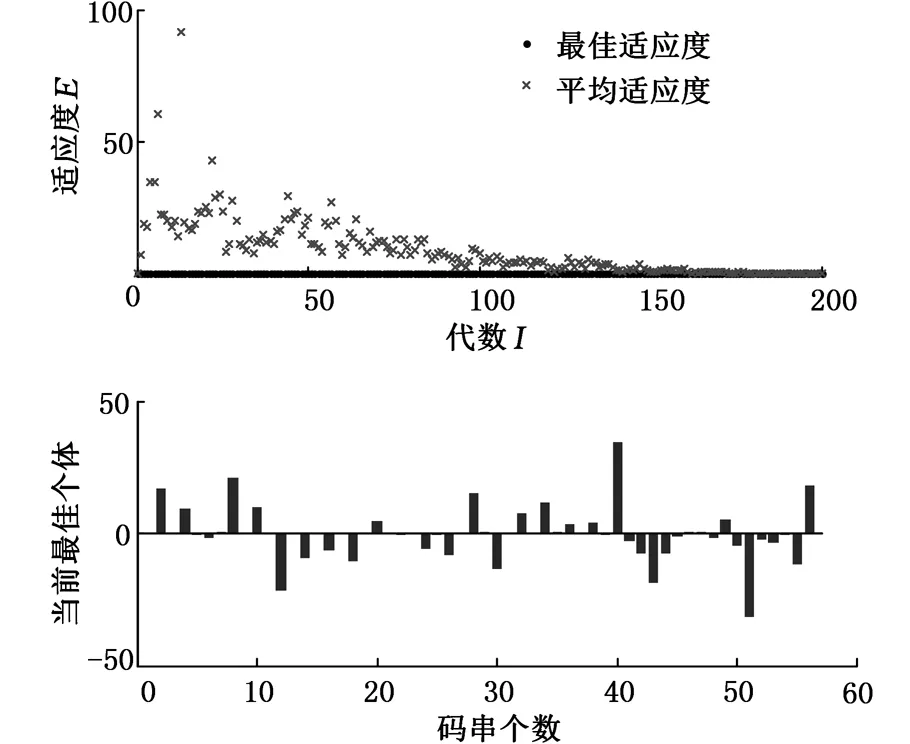
3 GA-T-S云推理网络板形识别的DSP实现





4 结论

