基于滑移率的线控制动系统制动力分配策略研究

彭晓燕　吕以滨　何　磊

湖南大学，长沙，410082



基于滑移率的线控制动系统制动力分配策略研究

彭晓燕吕以滨何磊

湖南大学，长沙，410082

为提高制动安全性和稳定性，针对四轮独立制动的线控制动系统，提出了基于滑移率的制动力最优分配策略及其约束优化问题的实时求解方法，并建立了Simulink与CarSim的联合仿真实验。仿真结果表明，所提出的制动力最优分配策略在不同的制动工况下始终能保证前轮滑移率大于后轮滑移率且后轮滑移率最优，既提高了汽车制动稳定性又能获得较短的制动距离。最后对最优制动力分配策略算法的实时性进行了实验验证，实验结果表明，所提出算法能够满足控制的实时性要求。

线控制动系统；制动力分配；滑移率；联合仿真

0　引言

新能源汽车是未来汽车的发展方向，而纯电动汽车是国际公认的新能源汽车的最佳解决方案[1]。然而，相比于传统内燃机汽车，纯电动汽车所需要考虑的安全因素更多，安全系统的设计更加复杂。采用线控技术构建有关汽车安全性能的电子控制系统，可极大地提高汽车的安全性、可靠性和稳定性，该技术在现代汽车尤其是纯电动汽车上有着广泛的应用前景。线控制动系统(break-by-wire,BBW)将传统液压或气压制动执行元件改为电驱动元件，每个车轮都有独立的控制器来实现其制动力的控制[2]，故可以通过更优的制动力分配策略和控制算法来进一步提高汽车制动性能。

基于滑移率的制动力分配方法是一种较优的分配方法，而已有的分配策略大多是针对传统液压制动系统的。文献[3]利用逻辑门限控制方法使后轮滑移率始终小于或等于前轮滑移率。文献[4-5]提出使后轮的滑移率按固定比例追踪前轮的滑移率，文献[4]中的比例为一个固定比值，而文献[5]则将比值分成四段分别进行控制。文献[3-5]均只考虑了纵向制动力，未考虑横向稳定性。文献[6]针对牵引车提出了滑移率最优的制动力分配策略，此策略中各车轮滑移率的权值取值难以确定。文献[3-6]虽然都是基于车轮滑移率进行制动力分配的，但均未实现根据实际附着条件获得最优的制动力。

鉴于此，本文提出一种基于滑移率的四轮独立制动控制的制动力最优分配策略，结合路面辨识，实时求解出各车轮在不同路面下的最优滑移率，从而控制各车轮在实际路面下的最优制动力。在获得与传统的理想制动力分配方法相同的制动强度和制动减速度的前提下，新的制动力分配策略可使前轮滑移率总是大于后轮滑移率，从而在保证汽车制动时的方向稳定性、防止后轴先于前轴抱死而发生危险的侧滑的同时，使前后车轮制动力分配更加接近理想的制动力分配曲线，为制动力控制提供了最佳的制动参数。

1　制动车辆模型与轮胎模型

1.1直道制动车辆模型

选取一台轿车作为研究对象，忽略汽车的滚动阻力偶矩、空气阻力以及旋转质量减速时产生的惯性力偶矩，并假设路面状况条件不变且同轴车辆左右车轮的载荷相同。汽车在水平路面上制动时的受力情况如图1所示。图中，Fj为惯性力。

图1　直道制动时汽车受力图

汽车制动时，地面对前后轴的法向作用力FZf、FZr分别为

(1)

(2)

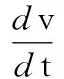
1.2轮胎模型

Burckhardt模型是由Burckhardt等经过理论变形和仿真分析提出的一种经验轮胎模型[7]。忽略汽车速度变化和轮胎载荷的影响，路面纵向附着系数的Burckhardt模型可表示为

(3)

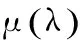
2　基于滑移率的BBW制动力分配策略

汽车的制动稳定性与制动时车轮是否抱死以及前后轮抱死的先后顺序有关。汽车制动时，理想的制动力分配是前后轴车轮的制动力能跟随汽车前后轴的动载荷的变化而变化，并保证前后轮能同时抱死以充分利用路面附着系数。实际的制动力分配应同时考虑制动稳定性与制动距离,并优先考虑制动稳定性。汽车制动时地面对车轮的横向反作用力FH的值越大，其抗侧滑能力越强。而FH的大小与车轮滑移率的大小有关。当滑移率λ=0，FH最大,随着λ的不断增大，横向附着系数迅速减小，从而令FH显著减小，这时只要很小的侧向力就有可能导致汽车发生危险的侧滑。

汽车制动时若后轮先抱死，则很小的侧向干扰力都极易使汽车发生侧滑，这是一种危险工况。因此针对线控制动系统的特点，为改善汽车制动时的侧向稳定性，设计汽车直道制动力分配策略如下：使车辆产生最大制动减速度以缩短制动距离，同时控制后轮滑移率小于前轮滑移率且使各车轮的滑移率保持在较小值，以改善汽车的制动稳定性。结合Burckhardt模型计算轮胎纵向制动力，则基于车轮滑移率的BBW制动力最优分配策略可转换为带不等式约束条件的非线性多变量函数的最优化问题，该问题的数学模型如下：

(4)

s.t.λr<λf

(5)

(6)

0≤λf≤1

(7)

0≤λr≤1

(8)

式中，λf、λr分别为单个前轮、后轮的纵向滑移率；FXf、FXr分别为单个前轮、后轮的地面制动力；μf(λf)、μr(λr)分别为单个前轮、后轮的纵向附着系数。

式(4)目标函数是在保证汽车方向稳定性的前提下，使滑移率保持在较小值。约束条件式(5)保证在任一制动强度下后轮滑移率小于前轮滑移率；约束条件式(6)保证前后车轴制动器的制动力之和等于总的附着力；约束条件式(7)、式(8)为滑移率的取值范围。

上述带不等式约束条件的非线性多变量函数的最优化问题的求解有很高的实时性要求，一般的优化算法难以满足其实时控制要求。因此本文针对上述约束优化问题提出一种新的实时优化计算方法：①采用文献[8]的方法获得不同路面下的μf(λf)、μr(λr)的表达式；②借助MATLAB优化工具箱中的求解非线性多元函数最小值的fmincon函数，离线求解出不同路面下的制动强度z与最优滑移率的关系曲线；③结合文献[8]路面辨识方法确定该路况下的制动强度z与最优滑移率的关系曲线，然后根据实际制动强度z实时计算出各车轮最优制动力。

本文选择一台轿车作为研究对象，空载时其参数如表1所示。

基于滑移率的制动力分配策略的最简单的方法是使汽车前后轮的滑移率相等。基于滑移率相等的制动力分配方法能达到理想的制动效果。但当汽车在变路面系数路面上制动时，不同的路面制动力系数与滑移率的关系不相同，紧急制动时汽车可能出现后轮先抱死的危险现象。

表1　空载整车参数

本文选取干沥青、湿沥青和雪地三种不同的路面分别对基于滑移率相等的制动力分配策略与本文提出的最优分配策略进行求解，结果如图2～图4所示,图中将基于滑移率的制动力最优分配策略称为优化方法，基于滑移率相等的制动力分配策略称为一般方法。

(a)滑移率

(b)制动力图2　干沥青路面滑移率与制动力比较

(a)滑移率

(b)制动力图3　湿沥青路面滑移率与制动力比较

计算结果表明，在同一路面及相同的制动强度下，基于滑移率的制动力最优分配策略与基于滑移率相等的制动力分配策略相比，汽车前轮制动力与滑移率都增大了，而后轮制动力与滑移率都减小了，且在任一制动减速度下，后轮滑移率始终小于前轮滑移率，从而提高了汽车制动时的稳定性。

(a)滑移率

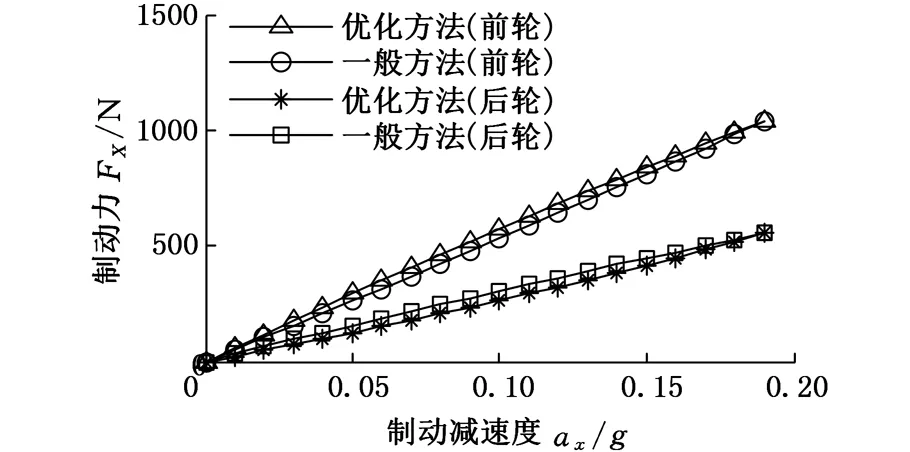
(b)制动力图4　雪地路面滑移率与制动力比较

3　仿真实验及分析

3.1仿真模型的建立

本文采用CarSim与MTALAB/Simulink两个软件对本文提出的最优分配策略进行联合仿真验证。分别建立基于滑移率相等的制动力分配策略与本文提出的最优分配策略的联合仿真模型，并进行仿真对比。CarSim软件用来进行车辆参数化建模，MTALAB/Simulink进行算法控制与仿真运行。制动力最优分配策略的仿真模型如图5所示。

3.2仿真条件及结果

为验证本文提出的最优分配策略的鲁棒性，分别在干沥青、湿沥青以及雪地三种路面下对汽车在不同的初速度、不同的制动强度下进行联合仿真，研究不同路面下本文所提出的最优分配策略的控制效果，包括汽车制动距离、地面制动力以及滑移率的变化情况。

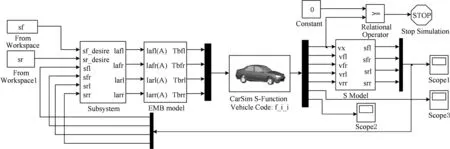
图5　基于滑移率的制动力最优分配策略的仿真模型

3.2.1干沥青路面仿真

汽车以不同的初速度v在干沥青直道路面上行驶，仿真终止速度为0。t=0时开始制动,t=1 s时制动强度直线上升到设定制动强度zp并保持不变。不同初速度和制动强度下车辆制动距离仿真结果如表2所示。仿真研究表明，不同的制动初速度和制动强度下汽车的实际地面制动力与滑移率的变化趋势是一致的。图6～图9所示为v=60 km/h，zp分别为0.5、0.75时的地面制动力和滑移率的仿真结果。

表2　不同初始车速与不同制动强度的制动距离

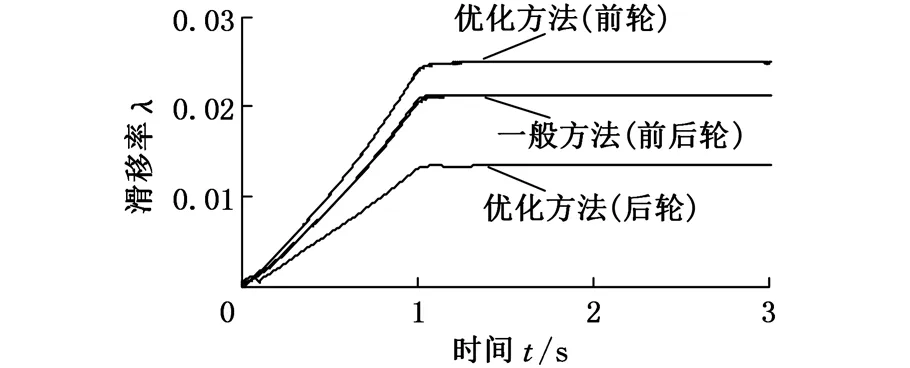
图6　初速度v=60 km/h、zp=0.5时的车轮滑移率

图7　初速度v=60 km/h,zp=0.5时的地面制动力

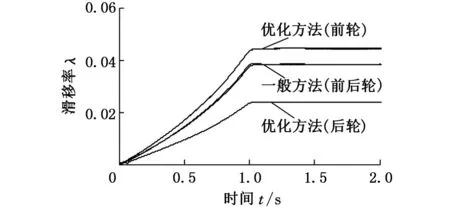
图8　初速度v=60 km/h,zp=0.75时的车轮滑移率

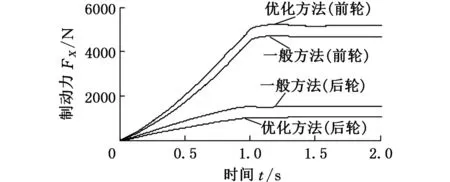
图9　初速度v=60 km/h,zp=0.75时的地面制动力

3.2.2湿沥青路面仿真

汽车以不同的初速度v在湿沥青直道路面上行驶，仿真终止速度为0。t=0时开始制动,t=1 s时制动强度直线上升到设定制动强度zp并保持不变。不同初速度和制动强度下车辆制动距离仿真结果如表3所示。仿真研究表明，不同的制动初速度与制动强度下汽车的实际地面制动力与滑移率的变化趋势是一致的。图10～图13所示为v分别为60 km/h、80 km/h，zp=0.75时的地面制动力和滑移率的仿真结果。

表3 不同初始车速与不同制动强度的制动距离

图10　初速度v=60 km/h,zp=0.75时的车轮滑移率

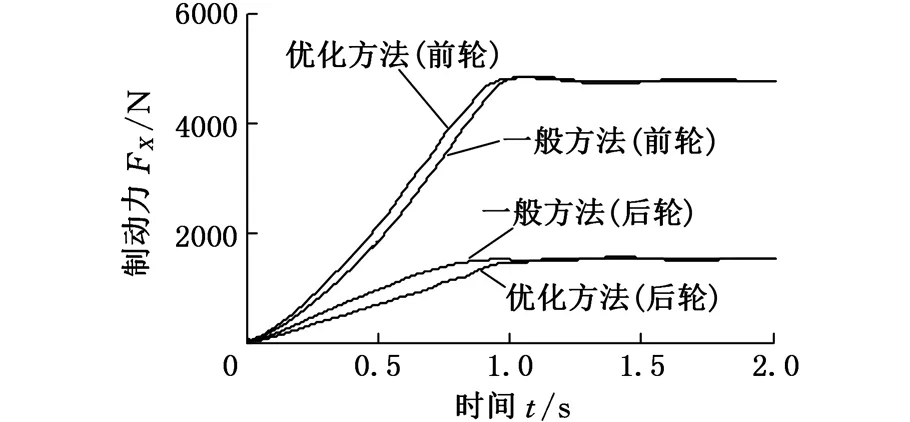
图11　初速度v=60 km/h,zp=0.75时的地面制动力

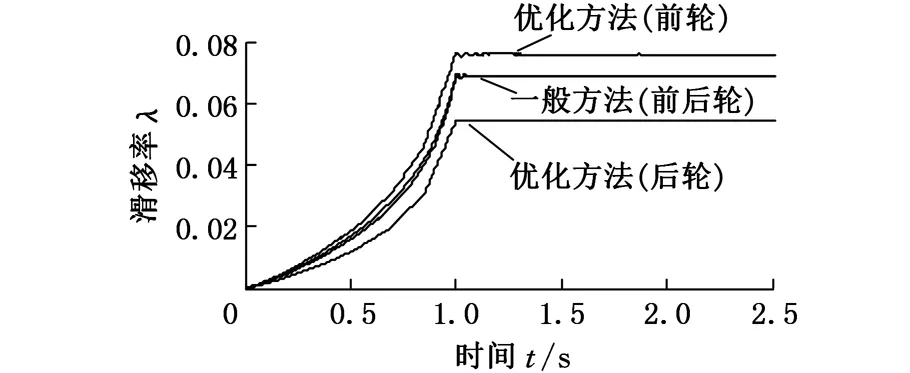
图12　初速度v=80 km/h,zp=0.75时的车轮滑移率

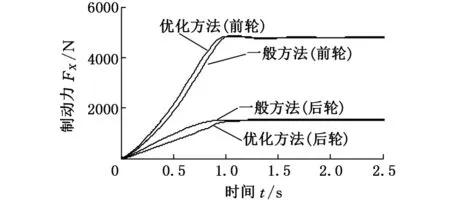
图13　初速度v=80 km/h,zp=0.75时的地面制动力

3.2.3雪地路面仿真

图14　初速度v=40 km/h制动时车轮滑移率

图15　初速度v=40 km/h制动时的地面制动力

汽车以40 km/h的初速度在雪地直道路面上行驶，仿真终止速度为0。t=0时开始制动,t=1 s时制动强度直线上升到zp=0.18并保持不变。两种制动力分配策略下的制动距离分别为36.15 m、36.04 m，车轮滑移率与地面制动力仿真结果如图14、图15所示。3.3仿真结果分析

从汽车在干沥青、湿沥青和雪地的仿真结果可以看出，常规制动且无车轮抱死时，在不同的直道路面、不同的初始速度以及不同的制动强度下制动时，采用本文提出的最优分配策略与采用基于滑移率相等的制动力分配策略相比，后轮滑移率始终小于前轮滑移率且小于基于滑移率相等的制动力分配策略的后轮滑移率，后轮滑移率越小，其所能产生的横向反作用力的值也大，有利于制动时的稳定性。

4　实验方案及算法实时性实验

4.1实验方案

本文设计的线控制动系统硬件在环实验如图16所示。dSPACE实时仿真系统主要用于实现整车模型的实时计算；主控制器和从控制器均采用飞思卡尔的MC9S12XF512单片机，主控制器负责计算分配四个车轮的最优制动力并将信息传给相应的从控制器；从控制器控制电子机械制动器(EMB)动作使车轮制动；主机监视系统实现人机交互，负责实时监视dSPACE实时仿真系统模型的运行状态。

图16　BBW硬件在环实验结构框图

在原有的液压防抱死制动系统(ABS)实验台的基础上，根据设计的BBW硬件在环实验结构框图，搭建了两轮BBW硬件在环实验台如图17所示。

图17　两轮BBW硬件在环实验台

4.2算法实时性实验

一般来说，ABS的控制周期为8ms时其控制效果较好[9]。为了达到较好的制动力分配效果，制动力最优分配策略算法在主控制器中的运算周期应小于8ms。为了验证算法的实时性，本文采用MC9S12XF512单片机实现最优制动力分配计算。采用示波器检测数据信号输出的时间间隔，实时计算时间间隔为7.12ms，满足实时性要求。

5　结论

(1) 提出的制动力最优分配策略在常规制动时既提高了汽车的制动稳定性，又能保证获得较短的制动距离，从而提高了车辆制动时的安全性。

(2)将制动力分配问题转换为约束优化问题，提出了其约束优化问题的实时求解方法，并进行了联合仿真验证。

(3)制动力最优分配策略算法在实际的控制器中运行能满足实时性要求，验证了制动力最优分配策略的可行性。

后续的研究中，将实现线控制动系统的制动力最优分配策略的硬件在环实验及实车测试实验。

[1]HuX,MurgovskiN,JohannessonLM,etal.Opti-malDimensioningandPowerManagementofaFuelCell/BatteryHybridBusviaConvexProgramming[J].JournalofBusinessEthics, 2015,20(1): 457-468.

[2]LiuJun,FuYongling,WangZhanlin,etal.Develo-pmentofBrake-by-wireHardware-in-loopsimulati-onBench[C]//2012InternationalConferenceonC-omputerDistributedControlandIntelligentEngineeringApplication.Changsha, 2012:1413-1417.

[3]李道飞.基于轮胎力最优分配的车辆动力学集成控制研究[D].上海:上海交通大学, 2008.

[4]FennelH.MethodforControllingBrakeForceDist-ribution.USPatent. 6322169[P].2001-11-27.

[5]张文利.基于滑移率的ABS_EBD控制策略研究[D].长春:吉林大学,2008.

[6]GoodarziA,BehmadiM,EsmailzadehE.AnOptim-isedBrakingForceDistributionStrategyforArticul-atedVehicle[J].VehicleSystemDynamics, 2008, 46(9):849-856.

[7]程斌.纯电动汽车再生制动与ABS匹配控制研究[D].合肥:合肥工业大学,2014.

[8]彭晓燕,章兢,陈昌荣. 基于RBF神经网络的最佳滑移率在线计算方法[J]. 机械工程学报,2011,47(14):108-113.

PengXiaoyan,ZhangJing,ChenChangrong.CalculationofRBFNeuralNetworkBasedOptimalSlipRatio[J].JournalofMechanicalEngineering, 2011,47(14):108-113.

[9]于良耀,王会义,宋健,等.汽车ABS液压系统性能评价与试验研究[C]//第四届全国流体传动与控制学术会议.大连，2006:39-43.

(编辑卢湘帆)

作者简介：彭晓燕，女，1965年生。湖南大学机械与运载工程学院教授。主要研究方向为复杂系统计算机控制、汽车电子与控制。吕以滨，男，1989年生。湖南大学机械与运载工程学院硕士研究生。何磊，男，1991年生。湖南大学机械与运载工程学院硕士研究生。

ResearchonBrake-forceDistributionStrategiesforBrake-by-wireSystemBasedonSlipRatio

PengXiaoyanLüYibinHeLei

HunanUniversity,Changsha,410082

Toimprovebrakingsafetyandstability,anoptimalbrakingforcedistributionstrategyforbrake-by-wiresystemoffour-wheelindependentbreakbasedonslipratioandarealtimeoptimizationcalculationmethodfortheconstrainedoptimizationproblemwereproposed,andaco-simulationmodelofSimulinkandCarSimwasestablishedtosimulateandtest.Thesimulationresultsshowthattheoptimalbrakingforcedistributionstrategybasedonslipratiomayalwaysensurethefrontwheelslipratiogreaterthantherearwheels’andtherearwheelslipratioisoptimalunderdifferentbrakingconditions,whichimprovesvehiclebrakingstabilityandobtainsshorterbrakingdistance.Atlast,theoptimalbrakingforcedistributionstrategyalgorithmisverifiedanditmeetstherequirementsinreal-time.

brake-by-wiresystem;brakingforcedistribution;slipratio;co-simulation

2015-11-02

国家自然科学基金资助项目(51575167)

U461.5; U461.91

10.3969/j.issn.1004-132X.2016.17.023

刘明周，1968年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为制造过程监测与控制、人机工程。阿地兰木·斯塔洪，男，1989年生。合肥工业大学机械与汽车工程学院硕士研究生。扈静，女，1976年生。合肥工业大学机械与汽车工程学院副教授。张淼，男，1986年生。合肥工业大学机械与汽车工程学院博士研究生。钱佩伦，女，1993年生。合肥工业大学机械与汽车工程学院硕士研究生。