借助三角形中角的关系巧解题
2016-09-28 06:52陕西任艳宁
高中数理化 2016年17期
◇ 陕西 任艳宁
借助三角形中角的关系巧解题
◇陕西任艳宁
在解三角形问题中除了常用的正弦定理、余弦定理及三角形面积公式以外,若能准确把握各角之间的关系,往往能快速找到问题的突破口.下面就这些关系的应用举例说明.
1 利用三角形内角和定理


(2) 求tanC的值.




2 利用三角形外角定理
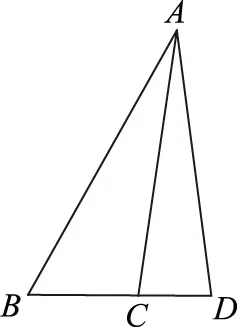
图1

(1) sin∠BAD;
(2)BD,AC的长.


所以
sin∠BAD=sin(∠ADC-B)=sin∠ADCcosB-

(2) 在△ABD中,由正弦定理得

在△ABC中,由余弦定理得
AC2=AB2+BC2-2AB·BC·cosB=

所以AC=7.


欲继续求解,需要借助sin2∠BAD+cos2∠BAD=1,计算较为烦琐,致使解题半途而废.因此解题中要注意转化的方向,尽可能地用已知来表示未知.
3 利用两角互补关系

图2



即

在△ADC中,由正弦定理得

即
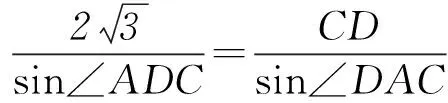
又sin∠BDA=sin∠ADC,BD=CD,所以∠DAC=90°, ∠BAC=120°.
在△ABC中,由余弦定理
BC2=AB2+AC2-2AB·ACcos∠BAC,
得
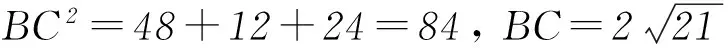

4 利用2角互余关系

(1) 求B的值;
(2) 若点E、P分别在边AB、BC上,且AE=4,AP⊥CE,求AP的长.

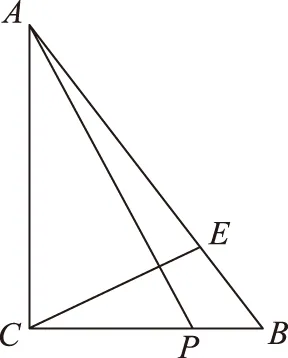
图3



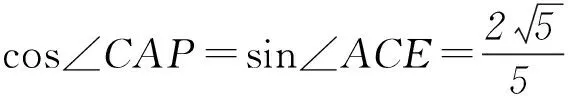
所以在Rt△ACP中,



陕西省渭南市大荔县城郊中学)
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
小学生学习指导(中年级)(2021年4期)2021-04-27
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
初中生学习指导·提升版(2020年12期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
读书文摘(下半月)(2019年12期)2019-09-10
中学生数理化·高一版(2018年6期)2018-07-09
理科考试研究·高中(2017年7期)2017-11-04
智富时代(2017年4期)2017-04-27

