例析曲线运动的相遇问题

◇　四川　晏小华



例析曲线运动的相遇问题

◇四川晏小华

对物体运动的研究是高中物理中的重要内容之一,从最基础的匀速直线运动到变速直线运动,再到曲线运动,运动分析的难度及复杂程度不断加深．与直线运动相比,学生们对曲线运动的分析能力明显不足,尤其在曲线运动的相遇及追及上,构件物理模型、选择求解公式是学生公认的难题．本文将对求解中物理过程的分析、物理模型的构建及使用的物理关系和规律进行讨论,通过相关问题的分析与讨论,培养学生系统化分析问题的能力．

1　2个平抛物体的相遇问题

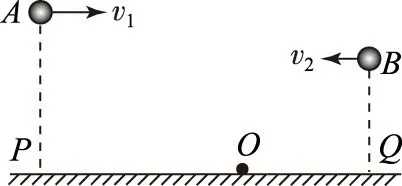
图1

APO∶OQ=v1h1∶v2h2;

DPO∶OQ=h1∶h2

2　平抛运动与匀加速运动的相遇问题

图2

(1) 抛出点O距离斜面底端的高度;

(2) 滑块与斜面间的动摩擦因数．

此时,结合图形中的几何关系可知

h=y+xtan 37°=1.7 m．

mgsin 37°-μmgcos 37°=ma,

将对应数据带入,可以求得μ=0.125．

3　平抛运动与匀速圆周运动的相遇问题

图3

总之,曲线运动的相遇问题是高中物理考核的重点内容之一,其变化性大、综合性强、联系广泛．在实际教学和学习过程中,应尽可能多关注综合性的曲线运动,将匀速直线、匀速圆周、匀加速直线等运动模式相结合,提升综合解题能力．

四川省成都市第49中学校)