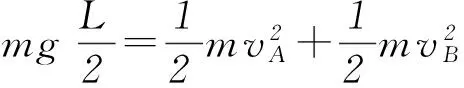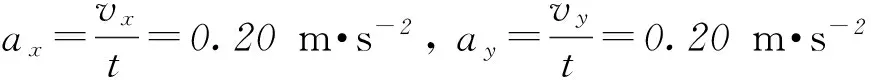整合知识要点研讨解题方法
———浅谈“运动的合成与分解”专题复习
◇ 浙江 成金德
整合知识要点研讨解题方法
———浅谈“运动的合成与分解”专题复习
◇浙江成金德
运动的合成与分解是曲线运动中的重点内容,典型的曲线运动(如平抛运动、斜抛运动、电场中的类平抛运动及在恒力作用下的匀变速曲线运动等)都可以通过运动的合成与分解得到有效解决.因此,如何正确理解和熟练把握运动的合成与分解的相关知识至关重要,本文就运动的合成与分解的知识和解题方法总结为5点,供大家参考.
1 1项法则
已知分运动求合运动的过程叫作运动的合成.已知合运动求分运动的过程叫作运动的分解.运动的合成与分解既是一个实际问题,也是一种思维方法.对于一个较为复杂的实际运动,可以看成是由几个典型的运动合成的,通过对典型分运动的研究和处理,得到复杂运动所需的结果.几个分运动的合成,结果是唯一的;合运动分解为几个分运动,结果不唯一.在具体分解中,往往按实际效果分解.
描述运动的物理量如位移、速度、加速度都是矢量,在进行运动的合成与分解时,都应遵循矢量运算法则,即运动的合成与分解法则.如果分运动都在同一条直线上,需选取正方向.与正方向相同的物理量取正,相反的物理量取负.矢量运算简化为代数运算,如果分运动互成角度,运动合成遵循平行四边形定则.
在速度的合成中,若存在相对运动的情形,则应利用经典的速度合成定理:动点的绝对速度等于其牵连速度与相对速度的矢量和.数学表达式为v绝对=v牵连+v相对.其中动点相对于静系的运动是绝对运动,动系相对于静系的运动是牵连运动,动点相对于动系的运动是相对运动.
2 2种模型
2.1渡河模型

图1
如图1所示,设河宽为d,水流速度为v水,船相对于静水的速度为v船,v水与v船间的夹角为θ,则船可以分解为2个分运动:沿水流方向的分运动,速度为v∥=v水+v船cosθ的匀速直线运动;垂直河岸方向的分运动,速度为v⊥=v船sinθ的匀速直线运动.渡河时间取决于v船的大小和方向.
1) 渡河时间最短.当v船垂直于河岸时,如图2所示,渡河时间最短,渡河时间为t=d/v船.
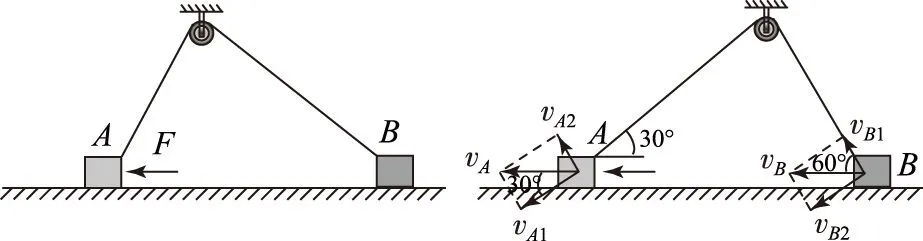
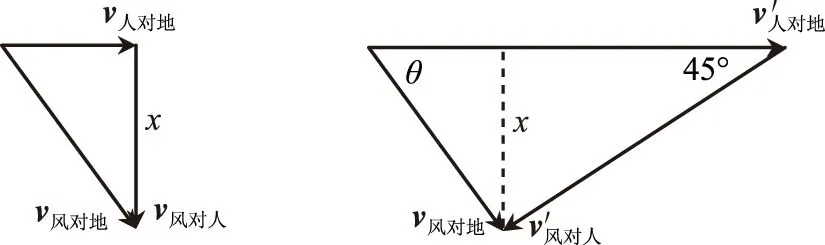
2) 渡河位移最小.当v船>v水时,船垂直渡河(合速度垂直于河岸)时位移最小,如图3所示,位移的大小等于河宽d.当v船 图2 图3 图4 2.2牵连模型 通过绳子或者通过轻杆连接的物体系统,称为牵连模型.如图5为绳子牵连模型,图6为轻杆牵连模型. 图5 图6 对于牵连模型,应抓住2个分运动: 绳牵连模型: 1) 沿绳方向的伸长或收缩运动,且沿绳方向分速度大小相等;2) 垂直绳方向的旋转运动. 杆牵连模型: 1) 沿杆方向的运动,且沿杆方向的分速度大小相等; 2) 垂直于杆方向的旋转运动. 在解决运动的合成与分解问题中,通常有3种解题方法. 3.1分解法 运动的合成与分解的一个基本原则就是按实际效果来进行分解.所以,在分解速度时,先确定物体实际运动的方向,这个方向就是合速度的方向,然后分析这个合速度所产生的实际效果,再确定2个分速度的方向. 分析在小船的运动过程中,沿水平方向的实际运动就是合运动,如图8所示,这个合运动可分解为: 图7 图8 分运动1:沿着绳子方向的分运动,此分运动使绳子收缩,其速度大小为v1=v船cosθ; 分运动2:垂直于绳子方向的分运动,此分运动使绳子绕滑轮转动,其速度大小为v2=v船sinθ. 由绳牵连模型的特点可知,沿绳子方向的分速度v1与绳子实际运动速度大小相等,即v1=v船cosθ=v,所以小船运动的瞬时速度为v船=v/cosθ. 3.2微元法 “微元法”是指在物体运动的过程中,选取一微小时间t,在此时间内,运动物体发生一段微小位移,然后利用数学极限思想,对运动进行分析的方法. 3.3能量法 能量守恒定律是自然界的一个普遍规律.应用能量守恒定律解决运动的合成与分解问题有时会十分凑效.现用能量守恒定律解答例1. 运动的合成与分解具有4个特性,在解决相关问题时要注意灵活应用. 4.1独立性 一个物体可以同时参与几个不同的分运动,各个分运动独立进行,互不影响.因此,在研究某个分运动时,可以将其他分运动隔离开来,就好像没有这些分运动一样,使研究的问题得到简化. 4.2同时性 合运动与分运动同时开始、同时进行、同时结束.合运动进行的时间和相应的各个分运动进行的时间相等.因此,只要知道某个分运动的时间,就知道了合运动或其他分运动的时间. 4.3等效性 合运动是由各个分运动共同产生的总运动效果,合运动与各个分运动总的运动效果可以等效替代. 4.4矢量性 加速度、速度、位移都是矢量,在进行合成和分解时,遵循平行四边形定则. 在学习和复习运动的合成与分解时,必须掌握以下5类典型问题的解题方法和技巧. 5.1渡河类 求解渡河类问题时,关键是弄清小船的2个分运动:沿河岸方向的运动,此方向的运动是由小船沿河岸方向的分运动与水流的运动的合成,这个分运动由小船和水流共同决定;垂直于河岸方向的运动,此方向的运动由小船单独决定,与水流运动无关. 图10 A2船在静水中的划行速率不同; B甲船渡河路程可能比乙船渡河路程小; C2船同时到达D点; D河水流速为dtanθ/t 5.2牵连类 求解牵连类问题时,应着重把握2点: 1) 沿着绳子(或轻杆)方向的分速度大小相等; 2) 物体的合运动往往可以分解为沿绳子(或轻杆)方向的分速度和垂直于绳子(或轻杆)方向的分速度. 图11 图12 分析对物体A,沿水平方向的实际速度vA即为合速度,vA可分解为沿着绳子方向的分速度vA1和垂直于绳子方向的分速度vA2,如图12,则vA1=vAcos 30°. 对物体B,沿水平方向的实际速度vB即为合速度,vB可分解为沿着绳子方向的分速度vB1和垂直于绳子方向的分速度vB2,如图12,则vB1=vBcos 60°. 由绳牵连模型的特点可知,沿着绳子方向的分速度大小必相等,即vA1=vB1. 图13 图14 对小球B,沿水平方向的实际速度vB即为合速度,vB可以分解为沿着轻杆方向的分速度vB1和垂直于轻杆方向的分速度vB2,如图14,则vB1=vBsin 60°. 5.3光点(或影子)移动类 求解光点(或影子)移动类问题时,应把握光点(或影子)移动的速度,此即为合速度,它可以分解为沿着光线方向的分速度和垂直于光线方向的分速度. 图15 图16 5.4有相对运动的速度合成类 在速度合成和分解中,若出现相对运动时,应选择经典速度合成定理求解.求解时务必弄清3个速度:绝对速度、相对速度和牵连速度.再通过速度矢量的几何关系建立方程. 分析本题的动点是风,动系是人,静系是地.绝对速度指风对地的速度v风对地,牵连速度指人对地的速度v人对地,相对速度指风对人的速度v风对人. 当自行车向正东以v人对地=5 km·h-1的速度行驶时,人感觉风从正北方向吹来,根据经典速度合成定理,有v风对地=v人对地+v风对人,如图17所示. 图17 图18 由图17可知 5.5恒力作用下的曲线运动类 在研究一些复杂的运动时,一般先分解为2个简单的分运动,通过研究这2个简单的分运动,再利用运动合成的方法,得到合运动的规律.这种方法尤其适用于对恒力作用下的物体的运动情况. 分析小球的运动可分为3个过程:第1过程小球做匀加速直线运动;第2过程小球做“类平抛运动”;第3过程小球做匀减速直线运动. 在第1过程中,小球受电场力作用,根据牛顿第二定律得小球的加速度为a=QE/m=0.20 m·s-2. 经过1 s小球沿x轴方向的速度大小vx=at=0.20 m·s-1,速度的方向沿x轴正方向. 经过1 s小球沿x轴方向运动的位移 x1=at2m/2=0.10 m. 在第2过程中,电场方向沿y轴正方向,小球做类平抛运动.可分解为沿x轴方向、速度为vx的匀速运动和沿y轴方向、初速度为0的匀加速运动. 在第2秒内,小球沿x方向运动的位移 x2=vxt=0.20 m. 在第2秒内,小球沿y方向运动的位移 y2=at2/2=0.10 m. 在第2秒末,小球在x方向的分速度仍为vx,在y方向的分速度vy=at=0.20 m·s-1. 由此可知,此时小球的运动方向与x轴成45°角.要使小球速度变为0,则在第3秒内所加匀强电场的方向必须与此运动方向相反,即指向第三象限,与x轴成135°角. 在第3过程中,设小球在电场作用下,小球加速度的x分量和y分量分别为ax、ay,由速度公式得 在第3秒内小球在x方向运动的位移 在第3秒内小球在y方向运动的位移 所以小球在第3秒末到达的位置坐标(x,y)为 x=x1+x2+x3=0.40 m,y=y2+y3=0.20 m. 总之,在求解运动的合成与分解问题时,关键是弄清哪个是合运动,这个合运动产生哪几个效果,可以分解为哪几个分运动,再作出速度分解示意图,根据几何关系求出结果. 浙江省义乌市第二中学)
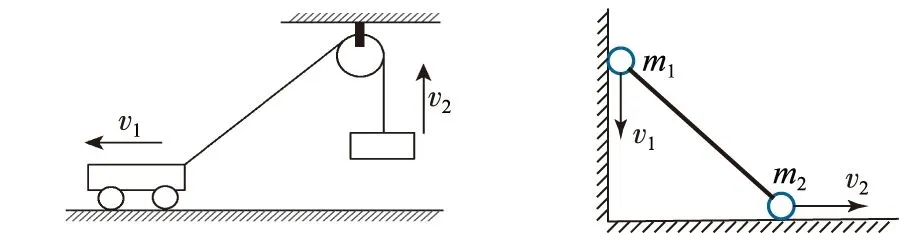
3 3条思路




4 4个特性
5 5类题型