2016年北京高考部分数学试题创新点赏析

◇　北京　崔用亮　王芝平(特级教师)



2016年北京高考部分数学试题创新点赏析

◇北京崔用亮1王芝平2(特级教师)

2016年高考北京数学试卷严格遵循秉承以往数学命题理念、突出数学特点、注重能力立意,着重考查对数学核心内容的理解与运用.在全面考查数学基础知识、基本技能、基本数学思想和基本数学活动经验的同时,尤其关注考生的理性思维和数学表达能力,较好地考查了考生的数学核心素养,体现了数学的教育价值.试题纯净淡雅、平而不俗,稳中有变、变中有新,题在书外、根在书内.在考查数学理性思维、核心素养的同时试题难度有所降低,给考生亲切、平和的感觉,顺应构建和谐社会的需要,有利于素质教育的实施,有利于促进数学教育变革的发展,对中学数学教学有积极而正确的引领作用.

1　深度刻画动态模型中的变与不变

A乙盒中黑球不多于丙盒中黑球;

B乙盒中红球与丙盒中黑球一样多;

C乙盒中红球不多于丙盒中红球;

D乙盒中黑球与丙盒中红球一样多

分析可对先后放入盒子的2个球进行分情况讨论:

1) 2个红球:乙盒中红球数+1.

2) 2个黑球:丙盒中黑球数+1.

3) 1个红球1个黑球: 先放红球,乙盒中黑球数+1; 先放黑球,丙盒中红球数+1.

由于情况3)所取的红球与黑球数相同,因此情况1)发生的次数与情况2)发生的次数相同,情况3)不影响乙盒中红球数与丙盒中的黑球数,故乙盒中红球数与丙盒中的黑球数相同.

近年来北京高考命制了很多创新型的数学开放性试题,注重与实际问题相结合,着重考查对于问题的分析能力、抽象概括能力.现实问题数学化,需要抓住核心变量,本题需要对取出的2个球颜色进行分类讨论,然后对过程进行分析,发现其中的变与不变,从而找出解决问题的方法.解决数学创新试题要关注“变”与“不变”的关系,准确提取“变”与“不变”的性质,并建立它们之间的逻辑联系.

2　深度挖掘数学量的核心原理与现实意义

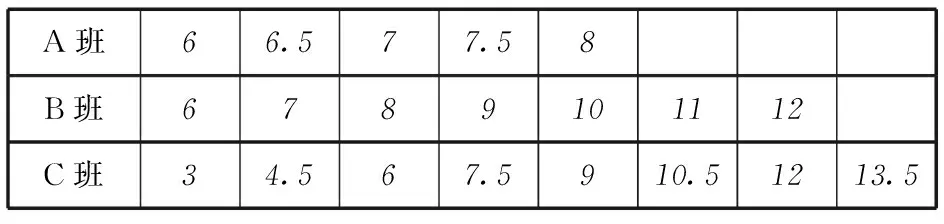
A班66.577.58B班6789101112C班34.567.5910.51213.5

(1) 试估计C班的学生人数;

(2) 从A班和C班抽出的学生中,各随机选取1人,A班选出的人记为甲,C班选出的人记为乙,假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率;

(3) 再从A、B、C 3个班中各随机抽取1名学生,他们该周的锻炼时间分别是7、9、8.25(单位:h),这3个新数据与表格中的数据构成的新样本的平均数记μ1,表格中数据的平均数记为μ0,试判断μ0和μ1的大小(结论不要求证明).

分析本题着重于考查对于现实数据的分析与处理能力,题目结构清晰、目的性强.同时,对于现实中的问题,考生需要抽象出相应的数学模型,因此考生结合数据对问题所包含的数学知识进行抽象概括.

对于第(1)问,通过分层抽样的数字特点即可得出答案;对于第(2)问,主要考查概率求解,着重于概率原理在现实问题中的运用;第(3)问主要考查平均数的性质,对于数学平均值,考生需要理解

即在一组数中添加一个等于该组数平均值的数,所得新的一组数的平均值不变. 对于离散型随机变量的数字特征,考生需要掌握其数学原理与现实意义.

3　从知识技能的运用到核心思想的回归

(1) 求a、b的值;

(2) 求f(x)的单调区间.

分析此题突破传统导数试题的设计模式,不是考生非常习惯的通过一次求导就可以简单地解决了的问题.当考生得到f′(x)=(1-x)e2-x+e后,通常根据f′(x)的正、负来求函数f(x)的单调区间,但是这个导函数的正负却不易判断.

但细细品味后,至少想到如下2条思路:

1)继续用导数研究这个“导函数”,这是因为研究一个函数的性质,导数是最基本的工具,突出了数学核心内容、思想的强大力量.所以由[f′(x)]′=(x-2)e2-x的正负易知,f′(x)的最小值为f′(2)=e-1>0,所以f(x)的单调区间为(-∞,+∞).

2)“化繁为简”——用简单的数学对象刻画复杂的数学对象,这是破解综合问题的重要策略.注意到f′(x)=(1-x)e2-x+e含有恒大于0的式子e2-x,不妨将其“提出来”,即得到

f′(x)=(1-x)e2-x+e=e2-x(1-x+ex-1).

而欲知1-x+ex-1的正、负，可以通过研究与其本质相同的简单函数ex-x的正、负得到,联想教材习题(人教A版《选修2》第2章第32页B组1(3)) 即知ex-x>0恒成立,当然这个结论需要完整地证明.所以f′(x)>0恒成立,所以函数f(x)的单调区间为(-∞,+∞).

4　对规律探索、运用能力的综合深入考查

(1) 对数列A:-2,2,-1,1,3,写出G(A)的所有元素;

(2) 证明:若数列A中存在an使得an>a1,则G(A)≠∅;

分析第(1)问通过套用规则让考生熟悉新定义问题的基本原理.第(2)问在第(1)问的基础上考查考生分析问题的能力.第(3)问着重考查对“G时刻”的理解,同时考查考生能否在短时间内掌握新知识点、原理、探索规律并运用规律解决实际问题的能力.

本题所体现的数学原理可以认为是现实问题的体现,就好比是“人生”,从a1开始起步(定义a1=0,即人生从0开始起步),到第k年人生已经达到ak的高度.人生有起有落,如果在第n年人生有了实质性突破,相对以往达到了前所未有的高度,那么这一年可以认为是成功的的一年,即G时刻.故G(A)即为相对以往达到前所未有的高度的年份构成的集合.

第(1)问易知在第2年与第5年达到了前所未有的高度,因此G(A)={2,5};第(2)问可以理解为如果人生中含有人生高度比人生初年高的年份,那么这段岁月中至少有1年是成功的,即这一年达到了相对以往更高的人生高度.

对于第(3)问,假设1个人每年在上一年的基础上所增长的人生高度最大值为1,则此人人生高度的增长最多能够达到自己年龄的增长.

1)如果此人每年都在走低,没有成长,那么相对初年的人生高度差为负,同时也没有成功的年份,即人生没有G时刻.

2)如果此人每年都能达到前所未有的高度,显然此人成功的年份就是自己的年龄,而人生的高度最大才是自己的年龄(此时每年都增长1个单位的人生高度,可以理解为“最好人生”).

3)如果此人的人生有起有落,那么人生高度降低的年份将不会是成功的年份,同时人生高度也会在理论上“最好人生”的基础上至少减少1个单位高度.此时人生高度的增长也会落后于年龄的增长,故那些成功的年数将超过这个人的人生高度.

因此,这道题在提醒我们,如果一个人能使自己所度过的每一年都成为成功的年份,并且每年都能达到人生最大的增长高度,这就是“最好人生”.

(3) 证明:若数列A满足an-an-1≤1(n=2,3,…,N),则G(A)的元素个数不小于aN-a1.