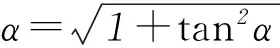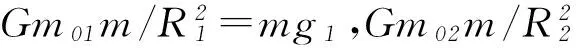例谈平抛运动进阶复习

◇　北京　罗倩敏(特级教师)



例谈平抛运动进阶复习

◇北京罗倩敏(特级教师)

平抛运动是一个典型的曲线运动,涵盖丰富,如运动学物理量、运动合成与分解、牛顿第二定律、动量定理、动能定理、机械能守恒等.其关联生活广泛,如打乒乓球、羽毛球、篮球,踢足球等.如何复习平抛运动令不少同学纠结不已,本文以平抛运动为例,构建“深化概念—整合规律—应用升华”进阶复习模式,以求抛砖引玉．

1　深化概念——认识平抛运动

基于实验再现情境,进行一定的数学分析、物理知识链分析或物理类比分析等达成深化概念的目的．

1.1实验认识——曲线运动

平抛运动是指物体以一定的水平初速度,仅在重力作用下的运动,平抛运动是一个过程,可选择一个体积小、密度大的钢球做实验,取一斜糟水平放置(末端水平),把小钢球放在斜糟某高度静止释放,用手机或相机等时连拍(频闪照相),相片上的小钢球的像点用平滑曲线连接起来为小钢球的轨迹,可见平抛运动的轨迹是曲线．

1.2数学认识——抛物线运动

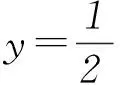
1.3物理认识——2个直线运动(至少有1个匀加速直线运动)的合运动

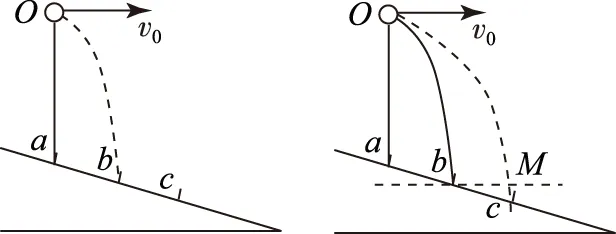
图1

将得到的平抛运动建立直角坐标系xOy,如图1．将小球分别投影到水平和竖直方向上,因水平方向不受外力，竖直方向仅受重力，故水平x方向有Δx=x2-x1=v0t-v0t=0,竖直y方向有Δy=y2-y1=gt2.可见,在相等时间t内,水平方向上相邻位移之差为0,故在此方向小球做匀速直线运动,竖直方向上相邻位移之差是恒量,故在此方向小球做匀加速直线运动,所以平抛运动是水平方向的匀速直线运动与竖直方向的自由落体运动的合运动,是一个匀加速曲线运动．

2　整合规律——平抛运动特征

基于概念,结合关联知识,进行一定的逻辑分析、推理、再实验等达成整合规律的目的．

1) 速度时刻改变,速度变化方向恒竖直向下,速度变化多少与平抛时间成正比.

因平抛运动的轨迹是抛物线,根据速度方向为所在点的切线方向,可推知平抛运动的速度的大小和方向时刻变化．由运动的合成与分解可知,水平方向速度不变,速度的变化只发生在竖直方向上,故速度变化方向恒竖直向下.或者根据牛顿第二定律可知,平抛物体的加速度由重力产生,故加速度方向和重力方向同向,恒竖直向下．由加速度定义得a=Δv/Δt=Δv/t,可见,速度变化多少与时间成正比．

2) 自开始运动至时间t，位移与水平方向夹角的正切值是t时刻末速度方向与水平方向夹角的正切值的一半.

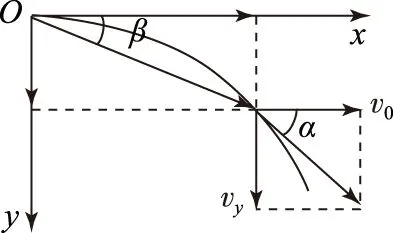
图2

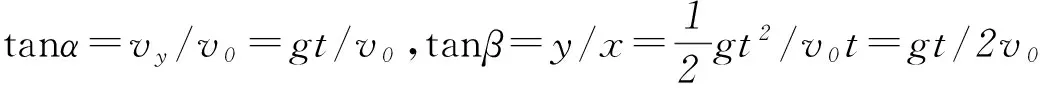
3) 自开始运动至时间t末的速度反向延长线将水平位移平分.

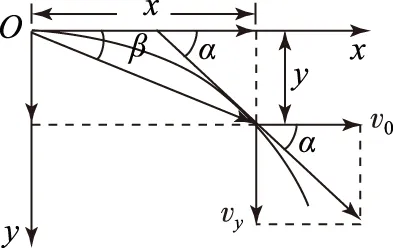
图3

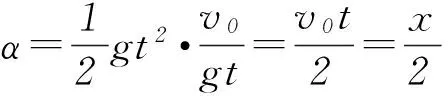
4) 相等时间内,速度变化、动量变化相等,重力作用的冲量与物体动量的变化均与时间成正比.

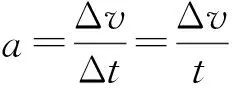
5) 重力的瞬时功率是对应时间内平均功率的2倍,且与平抛的时间成正比.

6) 平抛过程机械能守恒,物体动能变化的多少与平抛的高度成正比.

设物体质量为m,由于平抛过程只受重力作用,所以物体和地球组成的系统机械能守恒,由动能定理知,mgh=ΔEk．

3　应用升华——平抛运动题型赏析

基于典型的试题或情境,通过深化概念、整合规律、再实验等达成应用的目的．

3.1斜面上平抛

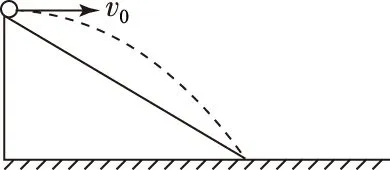
图4

(1) 求平抛的运动时间t随v变化的函数关系；

(2) 若落点在斜面上,设斜面倾角为θ,那么经过多少时间小球到斜面距离最大,最大距离是多少?

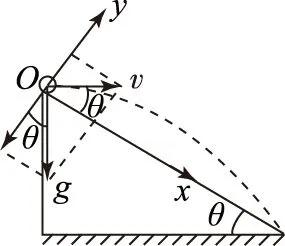
图5

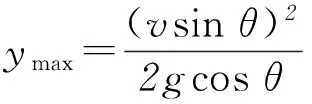
赏析斜面上平抛,是指平抛起点在斜面上,表现有单体不同速平抛或多体不同速平抛．若起、落点均在同一斜面上,求解的关键是抓住位移角、速度角的关系,明确位移角、速度角与初速度大小无关,平抛的时间与初速度成正比,当物体速度平行斜面时,到斜面有最远距离;若落点均在同一水平面,抓住平抛的时间相等,明确初速度越大,水平射程越大．

3.2平抛落在斜面上、圆弧上

图6

(1) 当其速度方向与斜面垂直,如图6所示，求小球在竖直方向下落的距离与在水平方向通过的距离之比;

(2) 设小球初速度为v0,当小球落在斜面上且速度方向不垂直于斜面时,求小球起点与落点连线的最小距离s．

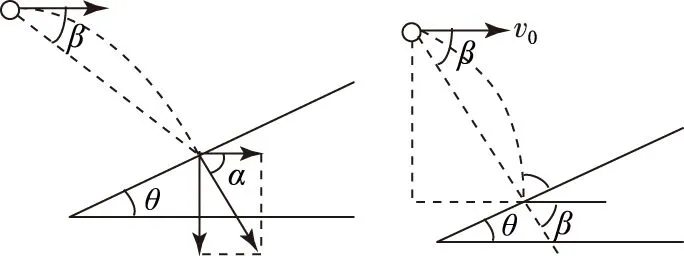
图7　　　　　　　　　图8

Av0

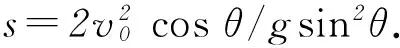
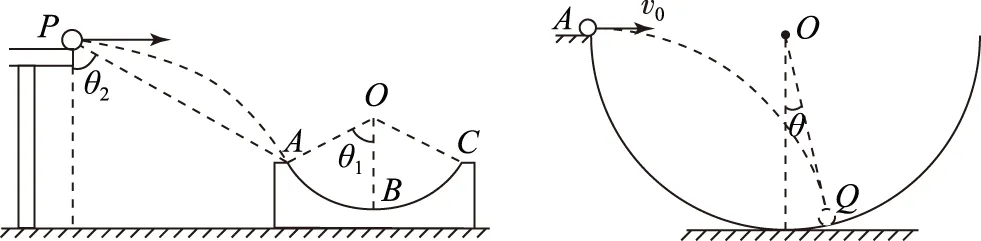
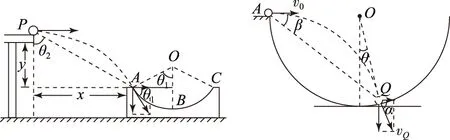
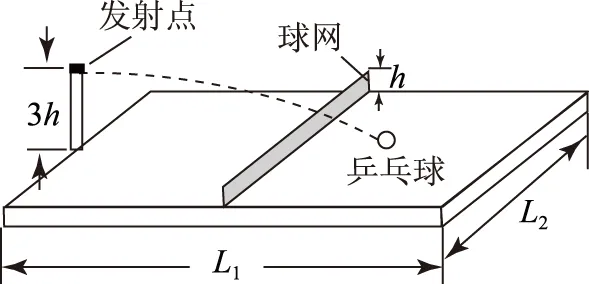
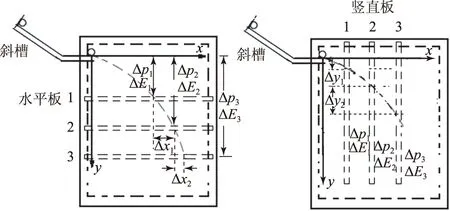
C2v03v0

图9　　　　　　　　　图10

(1) 求θ1、θ2的关系．

(2) 若小球以初速度v0从半圆弧的左端口A平抛,落点在圆弧的Q点,已知圆心O点与Q点连线与竖直方向的夹角为θ,如图12所示,求小球落在Q点时的速度vQ的大小．

图11　　　　　　　　　　　图12

(2) 设圆的半径为R,连接AQ,作出平抛经过Q点的速度分解如图14所示,

tanβ=y/x=Rcosθ/(R(1+sinθ))=cosθ/(1+sinθ),

vQ=v0/cosα.

图13　　　　　　　　　　　图14

赏析平抛落在斜面上、圆弧上,是指平抛的落点在斜面、圆弧上．前者表现有速度或位移垂直于斜面;后者表现有速度相切于圆弧或平抛起点对齐于圆心,终点在圆弧内．求解的关键是抓住速度角或位移角与已知三角形或圆的关系,突出几何思维．

3.3障碍平抛

图15

(1) 求速率v的取值范围．

(2) 若乒乓球先落在左侧台面某点,弹起后恰好垂直球网边缘以速度v0水平飞过,求左侧弹起点到球网的水平距离．

赏析障碍平抛是指平抛物体与它物相遇，表现有边界制约的特点.求解的关键是抓住相遇点水平、竖直位移对应关系，或者相遇点的速度方向，巧用对称性.

3.4天体上平抛

(1) 试比较小球经过板1、2和2、3之间的水平位移大小,平抛起点依次到1、2、3处的机械能变化量和动量变化量．

(2) 若将水平板变成竖直挡板,让小球先后3次做平抛,挡板位置依次放置1、2、3处,且保持相邻竖直挡板间位置间距相等,如图17所示,试比较小球经过板1、2和2、3之间的竖直位移大小,平抛起点依次到1、2、3处的机械能变化量和动量变化量．

(3) 若将(2)实验装置由地球表面移到月球表面来做,让小球先后3次做平抛,并确保释放点.竖直板1、2、3处位置和地球均相同,已知地球和月球的质量比为m1/m2=81/1,半径之比为R1/R2=4/1．试求在地球和月球表面平抛分别经过竖直挡板1、2过程的高度之比、动量变化之比、动能变化之比.

图16　　　　　　　　　　　图17

(2) 同理,因1到2的竖直平均速度小于2到3的,已知相邻两板的水平位移相等,故1到2的运动时间等于2到3的,所以有Δy1<Δy2.因机械能守恒,故有ΔE1=ΔE2=ΔE3.因起点分别到1、2、3处的时间不断增长,由动量定理得Δp1<Δp2<Δp3．

ΔEk地12/ΔEk月12=g1y地12/g2y月12=81/16．

赏析天体上平抛是指在不同星球表面上的平抛运动,表现出一些参量有一定对比性的特点．求解的关键是将不同天体表面处的重力加速度进行类比,明确求重力加速度的多种方法,寻找参量隐含决定的因素．

北京市第十八中学)