一道课本例题的拓展探究

◇　陕西　蒲　浩



一道课本例题的拓展探究

◇陕西蒲浩

一题多变的训练是拓展解题思维,培养良好数学素养的重要策略．在平时的解题练习中,可适当展开一题多变的训练,即改变原题内容、条件、形式或结论等,生成几道新题目,进而从多层次、多方位深入探索,把握问题实质,变中发现“不变”,从中发掘解题规律、归纳解题方法．本文对一道解三角形的课本例题进行变式探究,以期抛砖引玉．

图1

由sinα=sin(π-α),建立上述2式的联系,从而得出欲证结论．

在此视角下可对问题进行如下变式,以锻炼同学们的解题思维．

1　改变结论,化边为角

图2

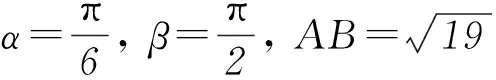
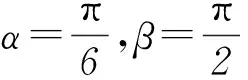
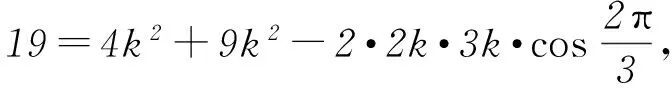
2　改变条件,化一般为特殊

图3

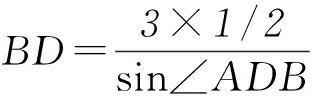
3　变换结论,逆向探究

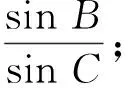
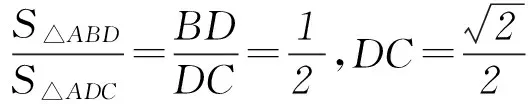
在△ABD和△ADC中,由余弦定理得

AB2=AD2+BD2-2AD·BDcos∠ADB,

AC2=AD2+DC2-2AD·DCcos∠ADC.

所以AB2+2AC2=3AD2+BD2+2DC2=6.

由(1)知AB=2AC,所以AC=1.

本文以一道课本例题为例,通过多方位思考,将试题进行了推广探究,从深层次上挖掘了课本例题功能,有力地激发了同学们的探究思维,进而培养了探究能力．

陕西省神木县职业技术教育中心)